Liceo cantonale di Locarno
Scoperta del funzionamento del
Sistema Solare
Lavoro di maturità di
Giulia Pinoja
Anno Scolastico 2014-2015
GIULIA PINOJA – LAVORO DI MATURITÀ
Sommario
1
Introduzione......................................................................................................................... 4
2
Uno sguardo al passato....................................................................................................... 5
3
4
5
2.1
Da Aristotele a Tolomeo ............................................................................................ 5
2.2
Da Tolomeo a Copernico ........................................................................................... 7
2.3
Da Copernico a Galileo .............................................................................................. 8
2.4
Da Galileo a Keplero .................................................................................................. 8
2.5
Keplero .......................................................................................................................... 9
Leggi di Keplero ................................................................................................................ 11
3.1
Legge delle orbite ellittiche ....................................................................................... 11
3.2
Legge delle aree .......................................................................................................... 13
3.3
Legge dei periodi ........................................................................................................ 15
3.4
Conclusione ................................................................................................................ 16
Newton ............................................................................................................................... 17
4.1
Contestualizzazione ................................................................................................... 17
4.2
Presentazione.............................................................................................................. 17
4.3
Da Galileo a Newton ................................................................................................ 18
4.4
Le leggi del movimento e la legge della gravitazione universale ......................... 19
4.5
L’intensità della forza gravitazionale ....................................................................... 22
4.6
Quattro regole del filosofare .................................................................................... 23
4.7
La Luna e la forza gravitazionale ............................................................................. 24
4.8
Excursus sul perché la Luna non è sempre piena ................................................. 25
Come sottrarsi all’attrazione terrestre ............................................................................ 27
5.1
6
Velocità di fuga .......................................................................................................... 27
Comete ................................................................................................................................ 29
6.1
Da dove arrivano ....................................................................................................... 29
6.2
Composizione............................................................................................................. 30
6.2.1
Composizione del nucleo ................................................................................. 30
6.2.2
Composizione della chioma ............................................................................. 30
6.3
Movimento orbitale di una cometa ......................................................................... 31
6.4
Acqua grazie alle comete .......................................................................................... 31
6.5
Le comete radenti di Kreutz .................................................................................... 32
6.6
Morte delle comete .................................................................................................... 32
6.7
La cometa di Halley ................................................................................................... 32
2
GIULIA PINOJA – LAVORO DI MATURITÀ
7
6.8
Molto di più ................................................................................................................ 33
6.9
Altri corpi minori ...................................................................................................... 34
6.9.1
Corpi minori ...................................................................................................... 34
6.9.2
Asteroidi ............................................................................................................. 34
6.9.3
Meteorite ............................................................................................................ 36
Esplorazione del sistema solare ...................................................................................... 37
7.1
Dall’antichità ad oggi ................................................................................................ 37
7.1.1
In passato ........................................................................................................... 37
7.1.2
Attualmente ....................................................................................................... 38
7.2
Parte per parte............................................................................................................ 39
7.2.1
Introduzione ...................................................................................................... 39
7.2.2
I razzi .................................................................................................................. 39
7.2.3
I missili................................................................................................................ 40
7.2.4
I satelliti .............................................................................................................. 41
8
Conclusione ....................................................................................................................... 42
9
Sitografia/Bibliogragia ..................................................................................................... 43
10
Indice delle figure.............................................................................................................. 44
3
INTRODUZIONE
1 Introduzione
Tutti noi oggi sappiamo com’è strutturato il sistema solare. Fin da piccoli ci viene
insegnato che i pianeti sono delle grosse palle sferiche, che ruotano attorno al Sole. Una
di queste è la Terra. Ci è stato detto che al centro del nostro sistema solare c’è il Sole e
noi abbiamo preso questa affermazione come vera, senza porci troppe domande. Ma
riflettendoci bene, qualcuno deve essere l’autore di questa scoperta.
Sicuramente non è stato sempre ovvio a tutti che il Sole si potesse trovare al centro
del nostro Sistema e che tutti i pianeti vi orbitassero attorno. Qualcuno deve aver
effettuato osservazioni su osservazioni e analizzato il fenomeno molto nel dettaglio, fino
ad arrivare a delle conclusioni soddisfacenti e sensate. Più volte mi sono chiesta chi sia
stato e come abbia fatto, così ho deciso di impostare il mio lavoro di maturità proprio su
quest’indagine: capire chi sia stato, e in che modo, a scoprire la struttura e il
funzionamento del nostro sistema solare
Con questo lavoro di maturità, innanzitutto, cercherò di spiegare, come già detto,
come si è arrivati a scoprire ciò che sappiamo oggi sul nostro Sistema Solare. Cercherò
successivamente di soffermarmi brevemente sui corpi minori come le comete, per finire
con l’esplorazione spaziale e gli strumenti di osservazione scientifica che l’uomo ha
inviato nello spazio allo scopo di studiare il Sole e gli altri pianeti.
L’andamento del mio lavoro di maturità seguirà un ordine cronologico: partiremo
infatti da Aristotele ed arriveremo fino ai nostri giorni.
4
GIULIA PINOJA – LAVORO DI MATURITÀ
2
Uno sguardo al passato
2.1 Da Aristotele a Tolomeo
Figura 1: Ritratto di Aristotele
La concezione geocentrica aristotelica1 vede la natura divisa in due realtà: celeste e
terrestre. La prima si estende dalla parte più lontana del cielo fino alla Luna, che è il
corpo celeste più vicino alla Terra, la seconda parte dalla Luna fino alla Terra che la
congloba e ne fa il centro dell’universo. Mentre i corpi terrestri sono composti di terra,
acqua, aria e fuoco, quelli celesti da un quinto elemento: l’etere. I cinque elementi per
Aristotele sono in moto, ma, mentre per i primi quattro il moto è vario quindi ritenuto
imperfetto, il quinto si muove di moto circolare uniforme ritenuto perfetto, perché è un
moto che non ha mai termine. Inoltre per Aristotele, la terra e l’acqua si muovono verso
il basso, l’aria e il fuoco verso l’alto. Inoltre, qualora ciascun elemento venga strappato
dal suo luogo naturale, tende a tornarvi. Ad esempio, il fuoco tende a portarsi dal basso
verso il suo luogo naturale, in alto. Spostandosi, gli elementi sono soggetti a movimenti
che Aristotele distingue in naturali e violenti. I moti violenti sono contro natura quindi
sono posteriori ai moti naturali. Ma qual’è la concezione fisica del moto? Secondo
Aristotele, per mantenere in moto un corpo con una certa velocità, è necessaria una
forza. Se questa forza è costante, essa produrrà una velocità costante. Si afferma infine
che la velocità di caduta di un corpo è proporzionale alla sua “pesantezza”.
1
Concetto ideato da Aristotele, 384 – 322 a.C.
5
UNO SGUARDO AL PASSATO
Figura 2: Ritratto di Tolomeo II Filadelfo
Qualche secolo più tardi Tolomeo di Alessandria1 riprese questo modello geocentrico
di Aristotele
Tolomeo, considerato il più grande dei geografi e degli astronomi di quei tempi,
scrisse un’importante opera, l’Almagesto2, che in seguito venne tradotto in arabo dal
greco e infine portato anche in Europa e tradotto dall’arabo in latino. Nell’Almagesto
Tolomeo perfeziona il modello dell’universo geocentrico in cui la Terra è situata al
centro di un universo sferico. I cieli sono strati fisicamente solidi e tra uno e l’altro ci
sono i pianeti, compresa la Luna e il Sole, questi ruotano sulla propria orbita attorno alla
Terra come del resto tutti gli altri pianeti. Ognuno di questi corpi celesti, oltre a ruotare
su orbite circolari, dispone di un centro che viene a sua volta trascinato dal moto
circolare di altre sfere celesti concentriche alla Terra. Ogni pianeta compie quindi due
movimenti sferici, il primo è un cerchio di piccole dimensioni, detto epiciclo il quale ha
il centro collocato su una seconda circonferenza di un cerchio di dimensioni più grande
detto deferente. Ai confini di queste sfere si situano le stelle fisse dopo le quali non
esiste niente se non Dio. Questo sistema, che riprende le concezioni cosmiche di
Aristotele, viene definito ‘sistema tolemaico-aristotelico’.
Figura 3: Sistema tolemaico-aristotelico
1
2
Claudio Tolomeo di Alessandria, 100 – 175 d.C.
Opera astroniomica, scritta attorno al 150 d.C.
6
GIULIA PINOJA – LAVORO DI MATURITÀ
2.2 Da Tolomeo a Copernico
Figura 4: Ritratto di Niccolò Copernico
Il modello Tolemaico restò valido per molti secoli, fino alle porte del quindicesimo
secolo ovvero fino a quando l’astronomo polacco Niccolò Copernico1 riprese la teoria
eliocentrica di Aristarco di Samotracia2. Per Aristarco il Sole era fermo e al centro
dell’universo mentre la Terra e gli altri pianeti giravano intorno ad esso con moti
circolari. Così si sarebbero spiegati con maggiore facilità i moti dei corpi celesti, tenendo
però anche in considerazione che la Terra oltre che girare attorno al Sole ruota anche
intorno al proprio asse. Copernico, in possesso dei dati delle osservazioni astronomiche
ripropose il modello eliocentrico.
Copernico aveva pure scoperto, oltre al fatto che la Terra ruota attorno al Sole, anche
che la Luna ruota attorno alla Terra. Nonostante questo, però, non abbandonò l’idea
che si trattasse di un universo sferico finito e delimitato dalle stelle fisse.
Con l’avvento di questa teoria si cominciò anche a mettere in dubbio il fatto che
l’essere umano fosse al centro dell’universo. Infatti l’intuizione di Copernico non venne
subito accettata, ma fu considerata come un’ipotesi, in quanto la si riteneva in contrasto
con la Bibbia, che pone l’uomo al centro del progetto creativo di Dio: era mai possibile
che Dio avesse collocato la creatura fatta a Sua immagine e somiglianza in un pianeta
periferico, che ruotava intorno al Sole e non piuttosto al centro dell’Universo?
Figura 5: Sistema eliocentrico
1
2
Niccolò Copernico, 1473 – 1543.
Aristarco di Samotracia, 310 – 230 a.C
7
UNO SGUARDO AL PASSATO
2.3 Da Copernico a Galileo
La nuova concezione eliocentrica del sistema solare di Copernico, che si può
considerare un timido precursore di quel rinnovamento culturale e scientifico che tra il
XVI e il XVII secolo avrebbe rivoluzionato il pensiero filosofico-scientifico europeo e
che avrebbe permesso poi di ridefinire i confini della scienza moderna, fu raccolta da
Galileo Galilei1, incurante che questa concezione avrebbe prodotto una fortissima
reazione da parte della Chiesa, dato che questo modello era in disaccordo con quello
proposto dalla Bibbia e in fin dei conti toglieva all’uomo la sua centralità nel mondo.
Infatti la chiesa difendeva il sistema geocentrico dicendo che la struttura dell’universo
dovesse essere quella spiegata nei testi biblici dell’Antico Testamento.
Galileo Galilei, che si dedicò allo studio della matematica e della fisica, era anche uno
sperimentatore: a lui si deve infatti il metodo di indagine scientifica cosi detto metodo
sperimentale, basato sulla riproduzione in laboratorio del fenomeno fisico in studio allo
scopo di individuarne e di verificarne la legge. Divulgò l’uso del cannocchiale, che
perfezionò e per mezzo del quale fece delle accurate osservazioni dei pianeti, che gli
permisero di negare la validità del sistema aristotelico-tolemaico. Tra le osservazioni
definitive vi fu la scoperta dei satelliti di Giove, che smentì palesemente la teoria
secondo la quale al centro di qualunque moto circolare ci fosse la Terra. Inoltre notò
anche le macchie solari, e le montagne sulla Luna, così riuscì a dimostrare che fossero
imperfette e non composte quindi dalla quintessenza.
Figura 6: Ritratto di Galileo Galilei
2.4 Da Galileo a Keplero
Galileo, quasi contemporaneo di Giovanni Keplero2, respinse decisamente
l’affermazione di Keplero che i pianeti si potessero muovere su orbite ellittiche,
sostenendo che solo l'orbita circolare aveva quel grado di perfezione che conviene al
moto degli astri. Eppure sappiamo che Keplero aveva ragione. Ma chi era Keplero?
1
2
Galileo Galilei, 1564 – 1642.
Giovanni Keplero, 1571 – 1630.
8
GIULIA PINOJA – LAVORO DI MATURITÀ
2.5 Keplero
Fin dalla nascita, il suo futuro venne programmato dai genitori. Egli diventò così un
ecclesiastico e si iscrisse all’università protestante di Tubinga, dove studiò teologia. In
quest’università insegnavano alcuni seguaci del copernicanesimo e uno di questi lo
convinse della validità delle teorie di Copernico (astronomo che affermava la teoria
eliocentrica). Più avanti Keplero cominciò a insegnare anche matematica e in seguito si
addentrò sempre di più nel campo astronomico, facendo previsioni astronomiche e
redigendo carte astrali. Già nel 1596 pubblicò un’opera, Mysterium cosmographicum, in cui
cercava di spiegare l’ordine dell’universo.
Il passo più decisivo lo compì quando nel 1599 divenne assistente di Tycho Brahe1
nel centro astronomico di Praga.
Grazie alle sue ricchezze e a una donazione del Re Federico II di Danimarca e
Norvegia, Tycho poté costruire il palazzo-osservatorio a Uraniborg e comprarsi gli
strumenti per effettuare misurazioni più precise e veritiere, ovviamente sempre ad
occhio nudo. Egli aveva una propria opinione sul sistema solare, che era una
combinazione tra l’idea tolomaica e l’idea copernicana. Brahe metteva la Terra fissa al
centro dell’universo, attorno alla quale ruotavano solamente il Sole e la Luna. Mentre
tutti gli altri pianeti ruotavano con orbite circolari attorno al Sole.
Figura 7: Sistema di Brahe
Nonostante questa teoria non sia stata molto rilevante per la scienza moderna, di
grande aiuto fu la grande quantità di misurazioni che effettua nell’arco della sua vita.
Queste dimostravano l’importanza di non accontentarsi solo di dati teorici ma fornirsi
anche di dati empirici in continuo aggiornamento.
Brahe dedusse tre altre cose molto importanti, che rivoluzionarono l’astronomia del
tempo. Con le sue osservazioni aveva notato che le comete tagliavano le orbite dei
pianeti. Da qui capì che le orbite non potevano essere qualcosa di materiale, ma
dovevano essere delle traiettorie seguite dai pianeti. La seconda invece venne scoperta
vedendo che ci sono astri nel cielo che appaiono e scompaiono (come le supernove).
Concluse quindi che, dato che l’universo può venire distrutto o generato come le
sostanze sulla Terra, le sostanze di quest’ultimo sono come quelle terrestri.
Infine la terza riguarda la sfericità delle orbite. Egli intuì che alcune orbite non sono
circolari, ma sono ovali, come ad esempio quella delle comete (cerchi ovali).
1
Tycho Brahe, 1546-1601. Rinomato astronomo danese con la passione di osservare le stelle.
9
UNO SGUARDO AL PASSATO
Ritorniamo a Keplero. Tycho lo chiamò al suo centro astronomico come assistente,
con uno scopo ben preciso. Tutti erano a conoscenza della bravura di Keplero nella
matematica, come pure della sua ingegnosità. Brahe gli affidò un compito che fino a
quel momento sembrava impossibile: determinare, grazie ai dati acquisiti dai due centri
astronomici di proprietà di Tycho (Praga e Uraniborg), le caratteristiche geometriche
dell’orbita di Marte. Nel 1601, Tycho Brahe muore, e Keplero gli succede nell’incarico
di matematico imperiale. Beneficiando delle eccellenti osservazioni astronomiche di
Tycho Brahe, Keplero, che è un osservatore mediocre a causa della sua miopia e della
sua cattiva salute, risolverà successivamente i vari parametri dell’orbita di Marte,
enunciando così le prime due leggi dei movimenti planetari che saranno pubblicate in
Astronomia nova seu de motu stellae Martis, nel 1609, a Praga.
Figura 8: Ritratto di Giovanni Keplero
10
GIULIA PINOJA – LAVORO DI MATURITÀ
3 Leggi di Keplero
3.1 Legge delle orbite ellittiche
L’impegno che Keplero si era prefissato era quello di trovare leggi rigorose capaci di
spiegare il funzionamento del cosmo mettendone in luce la struttura matematica.
L’occasione per riuscire in questa impresa fu offerta proprio dallo studio delle
caratteristiche geometriche dell’orbita di Marte. Basandosi sui risultati di Tycho Brahe,
tentò di spiegare queste caratteristiche geometriche dell’orbita di Marte con una
combinazione di moti circolari.
Ma Keplero, studiando e calcolando le orbite di Marte, dopo numerosi tentativi, si
rese conto dell’impossibilità che esse siano circolari in quanto in questa ipotesi si
avrebbe uno scarto di 8 minuti rispetto al moto reale. Abbandonata l’idea della
composizione dei moti circolari per descrivere l’orbita di Marte, riuscì a trovare
nell’ellisse la figura geometrica capace di conciliare i dati dell’osservazione con quelli che
aveva ottenuto attraverso il calcolo matematico. Keplero presentò le prime due leggi
nell’opera che lo rese famoso, Astronomia Nova, nel 1609.
Prima legge
I pianeti si muovono su orbite ellittiche di cui il Sole occupa uno dei due fuochi1.
Ricordiamo dalla matematica che l’ellisse è il luogo geometrico dei punti del piano
per i quali la somma delle distanze da due punti fissi, detti fuochi, è costante. Indicando
con 2a la somma delle distanze di un punto P dai fuochi si ha: PF1 + PF2 = 2a
Keplero però non riuscì a dare una giustificazione sia di questa legge come delle altre
sue due leggi. Fu Newton che circa 80 anni dopo riuscì a dimostrare che qualsiasi corpo
che si muova intorno ad un altro deve descrivere una “sezione conica”.
Pianeta
Sole
Perielio
Afelio
F1
F2
Cosa si intende per sezione conica?
Sezionando una superficie conica indefinita (ottenuta facendo ruotare di un giro
completo una retta attorno ad un'altra fissa aventi un punto in comune e formanti un
determinato angolo 𝛼) con un piano 𝜋, si ottengono le sezioni coniche. Variando
l’angolo di inclinazione 𝛽 del piano 𝜋 con l’asse r del cono, varia l’eccentricità.
1
Prima Legge, Legge delle orbite ellittiche, 1608.
11
LEGGI DI KEPLERO
Alcuni esempi di sezioni coniche: la parabola, l’iperbole, l’ellisse ed il cerchio.
Funzionamento:
r
Figura 9: Sezione conica
Quali sono le caratteristiche di un’ellissi?
Se consideriamo il rettangolo circoscritto all’ellisse di dimensioni 2a e 2b, possiamo
dire che a rappresenta il semiasse maggiore e b rappresenta il semiasse minore. Detta poi
c la distanza F1 e F2 tra i due fuochi, dei quali uno è occupato dal Sole, la forma
dell’orbita ellittica viene definita dalla sua eccentricità “e”, data dal rapporto c/a.
La Circonferenza risulta allora una particolare ellisse con eccentricità=0
(circonferenza eccentrica), l’eccentricità massima che può raggiungere un’ellisse è 1.
Fortunatamente a Keplero toccò di studiare Marte che è uno dei pianeti con
un’eccentricità maggiore, con un altro pianeta sarebbe stato molto difficile vedere se si
trattasse di un’ellissi o di un cerchio.
Il metodo migliore per costruire un’ellisse è il così detto metodo del giardiniere, che
consiste nel fissare due punte da disegno (fuochi) su una tavola di legno e fissare anche
una cordicella tra queste due punte. In seguito basta fare scorrere la punta di una matita
(punto O posizione istantanea della matita) lungo la cordicella (F1 O F2) tenendola
sempre tesa. Aumentando la distanza tra F1 e F2, aumentiamo anche l’eccentricità. In
questo modo è possibile ottenere un’ellisse perfetta. Il metodo si basa sulla definizione
12
GIULIA PINOJA – LAVORO DI MATURITÀ
di ellisse come luogo geometrico dei punti la cui somma delle distanze da due punti dati
(fuochi) è costante.
Figura 10: Ellissi
3.2 Legge delle aree
Seconda legge
In effetti viene definita “seconda legge di Keplero” ma in realtà è stata individuata
per prima da Keplero, nel 1602 (l’altra nel 1605).
Dai dati ricavati in seguito alle accurate osservazioni astronomiche sul moto del
pianeta Marte e della Terra, Keplero concluse che l’orbita della Terra era quasi circolare
e il Sole quasi al centro. Inoltre, conoscendo la traiettoria della Terra e la posizione del
Sole nei vari giorni dell’anno, per egli fu possibile stabilire in quale punto dell’orbita si
trovava la Terra in un dato istante e quindi capire anche la velocità con la quale si
muoveva. Keplero osservò che la Terra si muoveva più velocemente quando era
maggiormente vicina la Sole, quindi ipotizzò che fosse dovuto al fatto che il Sole
esercitava una forza sul pianeta che lo spingeva lungo l’orbita. Ovviamente minore era la
distanza Pianeta-Sole maggiore era l’intensità della forza.
Sempre dai dati in suo possesso, riuscì a verificare che le aree dello spicchio A-Sole-B
e dello spicchio D-Sole-C erano uguali (vedi figura qui di seguito). Trovò quindi la
relazione fra velocità del pianeta e la distanza dal Sole.
Tutti questi risultati gli permisero di enunciare la seguente legge delle aree:
Il segmento che congiunge un pianeta con il Sole spazza aree proporzionali agli
intervalli di tempo considerati1.
In altre parole, le aree descritte in uguali intervalli di tempo sono uguali, qualunque
sia la posizione del pianeta.
1
Seconda legge, Legge delle aree, 1609.
13
LEGGI DI KEPLERO
Figura 11: Legge delle aree
14
GIULIA PINOJA – LAVORO DI MATURITÀ
3.3 Legge dei periodi
Terza Legge
Nonostante le sue due grandi scoperte, Keplero non si sentì ancora soddisfatto. Egli
intuì che ci dovesse essere qualcosa in comune tra tutte le varie orbite del Sistema Solare
e i loro periodi di rivoluzione.
Si mise al lavoro e riuscì a trovare una relazione tra i tempi impiegati dai pianeti a
ruotare intorno al Sole (periodi) e le loro distanze medie dal Sole. Concluse questo
studio sui periodi dei pianeti formulando la seguente legge:
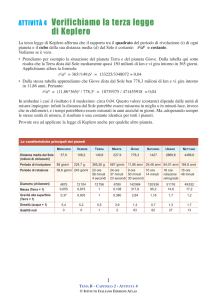
I quadrati dei periodi dei pianeti sono proporzionali ai cubi delle rispettive distanze
medie dal Sole1.
𝑎!
pianeta
𝑎!
Sole
pianeta
Per esempio, se 𝑎1 e 𝑎! sono i semiassi maggiori delle ellissi descritte dai due pianeti, i
cui periodi di rivoluzione sono rispettivamente T1 e T2 si ha: T12/ T22 = 𝑎!! / 𝑎!! .
1
Terza legge, Legge dei periodi, 1619.
15
LEGGI DI KEPLERO
3.4 Conclusione
Keplero ammette l’esistenza di una forza, che spingeva i pianeti lungo l’orbita,
localizzata nel Sole che anima il moto dei pianeti. A questo proposito facciamo parlare
Keplero: “ Un tempo credevo che la causa motrice dei pianeti fosse un’anima, invece lo
scopo che qui mi propongo è di affermare che la macchina dell’universo non è simile a
un divino essere animato, ma è simile a un orologio e in essa tutti i movimenti
dipendono da una forza attiva materiale, così come tutti i moti dell’orologio sono dovuti
al semplice pendolo”.
Si è già detto che Keplero non riuscì a spiegare la causa all’origine di questi moti - e
quindi la legge che permetteva di affermare che le orbite dei pianeti dovevano essere
delle ellissi - per cui le leggi di Keplero sono da considerarsi come leggi empiriche, che
riassumono tutte le sue osservazioni sperimentali.
Ad ogni modo non solo le leggi di Keplero furono confermate e spiegate da
scienziati successivi, ma esse valgono per ogni sistema orbitale di due corpi, anche per i
satelliti artificiali in orbita attorno alla Terra. Il rapporto costante T 2 / a3 (quadrato del
periodo di rivoluzione del pianeta diviso il cubo del suo semiasse) è valido per tutti i
pianeti e per tutti i satelliti artificiali della Terra.
Da segnalare la pubblicazione di tavole astronomiche da parte di Keplero, per la
compilazione delle quali si servì delle osservazione di Tycho e delle sue leggi. Queste
tavole, in uso fino all’arrivo dei telescopi ad alta precisione, permettevano di calcolare la
posizione dei pianeti in qualsiasi istante.
16
GIULIA PINOJA – LAVORO DI MATURITÀ
4 Newton
4.1 Contestualizzazione
Da Copernico in poi fino alla metà circa del sedicesimo secolo si era via via
consolidata nel mondo scientifico, attraverso gli studi e le osservazioni astronomiche,
l’accettazione del Sistema eliocentrico, secondo il quale il Sole è posto in uno dei fuochi
dell’ellisse descritta dal pianeta che ruota attorno al Sole e per Galileo il Sole è posto al
centro della circonferenza descritta dal pianeta che gli ruota attorno. È da notare che
Galileo rifiutò categoricamente di riconoscere che il moto di un pianeta attorno al Sole
fosse ellittico come sosteneva Keplero. Per Galileo il “moto naturale” non era il moto
rettilineo ed uniforme, ma il moto circolare uniforme. Sia Galileo che Keplero però
erano convinti dell’esistenza di una forza relativa al moto dei pianeti. Keplero si accorse
di un certo collegamento che poteva spiegare la forza emanata dal Sole per far muovere
i pianeti lungo l’orbita (credeva che il Sole “spingesse” i pianeti lungo l’orbita).
L’esistenza di questa forza gli permise, ad esempio, di affermare che i pianeti si
muovevano in maniera più rapida quando si trovavano vicino al Sole.
Keplero però non riuscì a dare una risposta alla domanda: “Qual’ è la natura di
questa forza che permette ai pianeti di muoversi intorno al Sole su delle orbite
ellittiche?”. La risposta a questa domanda, che condurrà a rivedere concezioni fino ad
allora accettate a favore di un nuovo modo di concepire la fisica celeste e terrestre, non
tardò ad arrivare ad opera di Newton su suggerimento di Robert Hooke.
4.2 Presentazione
Isaac Newton1 rimase orfano di padre all’età di tre anni. Quando anche il patrigno
morì, ricevette una notevole eredità che gli permise di intraprendere gli studi che
completò al Trinity College, studiando matematica, fisica e astronomia. Dopo un ritiro
di due anni nel suo villaggio natale a causa dell’imperversare di una pestilenza, ritorna
nel 1669 a Cambridge, dove gli viene assegnata una cattedra di matematica e
successivamente entra in Parlamento come rappresentante di questa Università. Fin da
giovane, Newton si fece notare per il suo attaccamento alle scienze e in particolare alla
fisica. Nel 1672 divenne membro della prestigiosa Royal Society di Londra e
successivamente nel 1703 ne divenne Presidente, carica che ricopri fino alla morte.
1
Isaac Newton, 1642 – 1727.
17
NEWTON
4.3 Da Galileo a Newton
Agli albori del nuovo metodo scientifico, di cui Galileo, come abbiamo già detto, fu
tra i primi degni rappresentanti, si fa strada un assioma, ricavato induttivamente nel
laboratorio della natura: “Ciascun corpo persevera nel suo stato di quiete o di moto
rettilineo uniforme se non è costretto a mutare tale stato per effetto di forze applicate al
corpo stesso”. Questo assioma è noto con il nome di primo principio della dinamica.
Molte furono le prese di posizione da parte di uomini di scienza, anche in vita, intese ad
attribuire a Newton la paternità del principio d’inerzia e non a Galileo (tra questi
scienziati figura René Descartes), fin quando Newton stesso, che notoriamente non era
molto incline a riconoscere i meriti altrui, affermò, in modo inequivocabile, che il
principio d’inerzia era stato formulato da Galileo. In effetti, nella sua opera, Philosophiae
naturalis principia matemathica, Newton scrisse: “Tutti questi principi sono accettati da ogni
matematico, e confermati da molteplici esperienze. In particolare dalle misure effettuate
da Galileo il quale trovò che la discesa dei gravi è proporzionale al quadrato del tempo, e
che il moto dei proiettili è parabolico”. Dopo questo riconoscimento, Galilei fu
universalmente considerato il “padre della scienza moderna”. (A Newton, invece, va il
merito di essere stato il primo a formalizzare le intuizioni di Galileo, collocando la
validità del principio d’inerzia nei cosiddetti “sistemi inerziali”.)
18
GIULIA PINOJA – LAVORO DI MATURITÀ
4.4 Le leggi del movimento e la legge della gravitazione
universale
Come accennato, il problema lasciato aperto dalle leggi di Keplero era quello del
perché i pianeti continuavano a ruotare intorno al Sole senza allontanarsene in
disaccordo con il principio d’inerzia di Galileo, secondo il quale un corpo non
sottoposto a forze o resta fermo o, se è in moto, si muove in modo rettilineo e
uniforme. Insomma, per inerzia, i pianeti dovrebbero allontanarsi dal Sole in linea retta e
a velocità costante. Fu Isaac Newton a dimostrare la soluzione: i pianeti sono trattenuti
da una forza che bilancia la forza centrifuga, dovuta al moto di rivoluzione. Più
precisamente: due corpi si attirano in modo direttamente proporzionale alla loro massa e
inversamente proporzionale alla loro distanza elevata al quadrato.
In altre parole, l'attrazione impedisce al pianeta di muoversi in linea retta e di perdersi
nello spazio, e lo costringe in pratica a «curvare» continuamente la propria traiettoria
verso il Sole, in un gioco di equilibrio tra l'attrazione gravitazionale e il moto di
rivoluzione, il cui risultato è l'orbita ellittica.
In realtà, non c'è solo interazione tra ogni pianeta e il Sole: un pianeta è anche
attratto dagli altri pianeti (debolmente, perché questi sono di piccola massa) e dalle stelle
circostanti (ancora più debolmente, perché esse sono lontanissime).
Figura 12: Forza circolare di una galassia
La forma circolare di questa galassia mostra che la forza di gravità possa valere anche
a distanze molto grandi.
Le tre leggi della dinamica
1. In assenza di forze, un "corpo" in quiete resta in quiete, e un corpo che si
muova a velocità rettilinea e uniforme continua così indefinitamente.
2. Quando una forza è applicata a un oggetto, esso accelera. L'accelerazione è
nella direzione della forza ed è proporzionale alla sua grandezza ed
inversamente proporzionale alla massa dell'oggetto.
3. Le forze sono sempre prodotte a coppie, con uguale grandezza e verso
opposto. Se il corpo n. 1 esercita una forza F sul corpo n. 2, allora il corpo n. 2
19
NEWTON
eserciterà sul corpo n. 1 una forza di uguale grandezza e di verso opposto.
La legge della gravitazione universale
Dopo la formulazione delle leggi sul moto sopra riportate, il secondo contributo di
Newton allo sviluppo della meccanica, fu la scoperta delle leggi dell’interazione
gravitazionale, cioè l’interazione tra due corpi, siano essi pianeti o piccole particelle, che
produce un moto descrivibile mediante le leggi di Keplero.
Newton non procedette, come potremmo fare oggi, a ricavare sperimentalmente
l’interazione gravitazionale fra due masse e dedurre la validità delle leggi di Keplero, ma
procedette in senso inverso, usò le leggi di Keplero e ricavò successivamente la forza
che si esercita tra due pianeti.
In primo luogo dedusse dalla legge delle aree (seconda legge di Keplero) che la forza
associata all’interazione gravitazionale è centrale (diretta verso il centro). Cioè la forza
agisce lungo la congiungente dei due corpi interagenti, esempio un pianeta e il Sole.
Semplificando il metodo di Newton, possiamo dire: dato che la prima legge di
Keplero stabilisce che l’orbita del pianeta è ellittica, consideriamo un caso particolare di
ellisse; il cerchio per il quale i due fuochi coincidono con il centro. In questo caso per la
seconda legge di Keplero la forza F è diretta verso il centro del cerchio. Così, sappiamo
che la forza centripeta responsabile del moto circolare uniforme, è :
20
GIULIA PINOJA – LAVORO DI MATURITÀ
essendo m la massa del pianeta in moto sulla traiettoria circolare attorno al Sole di massa
M e riferendo il moto di m a un sistema di riferimento solidale con M.
Ricordando poi che la velocità in un moto circolare uniforme è data da:
!!
v = 2πr/T e F = m a = m !
abbiamo:
F = 4π! mr/T !
Ma la terza legge di Keplero, nel caso particolare di un’orbita circolare, quando la
distanza media fra M ed m è il raggio del cerchio, diventa T ! = Kr ! (dove K è la
costante del rapporto T2 / R3. Pertanto
F = 4π! m/Kr ! o anche F = γm/r ! (1) essendo γ = 4π2/K
che dimostra che, per soddisfare le leggi di Keplero, l’interazione gravitazionale deve
essere centrale e inversamente proporzionale al quadrato della distanza,
Newton stesso controllò la correttezza della sua ipotesi, confrontando l’accelerazione
centripeta della Luna con l’accelerazione di gravità della Terra g ! = 9,81 m/s2.
L’accelerazione della Luna è:
al = v2/r = 4π2r/T2 con r = 3,84 x 10! m e T = 2,36 x 106s. Così
al = 2,72 x 10-­‐3m/s2 Pertanto g ! /al = 3602 = 602
Poiché il raggio della Terra è rT = 6,37x106 m, abbiamo che
(r/r! )2 = (384/6,37)2 = (60)2 cioè g ! /al = (r/rT)2 Nei limiti di precisione delle misure, le due accelerazioni risultano inversamente
proporzionali al quadrato delle distanze dei punti dal centro della Terra.
Le tre leggi di Keplero, come abbiamo avuto modo di accennare, non furono dedotte
dalle leggi della fisica, sono solo leggi empiriche valide per Marte, la Terra e tutti i pianeti
del sistema solare. Si deve a Newton e alla sua teoria sulla gravitazione se le leggi di
Keplero acquistano anche un fondamento fisico, perché sono la naturale conseguenza
della dipendenza della forza dal quadrato della distanza. Cioè se la forza attrattiva
dipende dall’inverso del quadrato della distanza, allora la traiettoria del corpo deve
essere necessariamente un’ellisse e viceversa. Newton riesce anche a dimostrare che la
forza di gravità dipende, oltre che dalla distanza tra i due corpi, anche dalle loro masse.
Ritornando alla (1), infatti, dato che ɣ = 4𝜋2/K del pianeta considerato è costante
(ma dipendente dal periodo T e dal semiasse maggiore r (nella esemplificazione dal
raggio)), Newton, rifacendosi alla sua formazione e alla sua facilità espositiva e
dimostrativa di natura geometrica, intuì (intuizione suffragata dalla terza legge della
gravitazione di cui sopra) che per simmetria doveva esercitarsi una forza del Sole sul
21
NEWTON
pianeta della stessa forma della (1), ma con la massa M del Sole al posto della massa m
del pianeta, ovvero:
F’ = γ’ M/r2 Dato che F = F’ per il terzo principio ne risulta: γ’ M/r2 = γm/r2 e quindi
γ’/m = γ/M se indichiamo con G questo rapporto costante possiamo scrivere
γ = GM, quindi: F = F’ = GMm/ r2 F!" = F!" = G ∙
Mm
r!
Questo risultato ci permette di dimostrare quanto affermato: la forza gravitazionale
dipende anche dalle due masse interagenti.
Newton aveva poca dimestichezza con la sperimentazione e non riuscì a trovare il
valore di G, anche perché tale forza gravitazionale, pur avendo un campo d’azione
teoricamente infinito, è una forza estremamente debole. 112 anni dopo Henry
Cavendish, nel 1798, servendosi di una bilancia di torsione, trovò per la costante di
gravitazione universale G il valore 6.67x10-11Nm2.
In conclusione, per Newton questa forza era la causa del moto di ogni pianeta; in
effetti questa forza non interagiva solo tra Sole e Terra, ma anche tra Giove e i suoi
satelliti, tra Luna e Terra e tra un qualsiasi corpo e la Terra. Dopo la pubblicazione dei
Principia parecchi furono gli oppositori di Newton, che lo accusavano di aver introdotto
con la gravità, delle forze occulte perché non era riuscito a spiegare cosa fosse la gravità.
4.5 L’intensità della forza gravitazionale
Eravamo rimasti a questa equazione
F! = G
m! m!
R!
dove m1 e m2, sono due masse qualsiasi nell’universo ed R la loro distanza tra i centri di
massa.
Ad alcuni potrà sembrar strano che Newton affermasse che le due forze in
contrapposizione sono le stesse tra due corpi anche se essi hanno masse m1 e m2 diverse.
Vediamo perché.
Come sappiamo, 1 kg di materia attrae con forze uguali e contrarie un altro kg di altra
materia
22
GIULIA PINOJA – LAVORO DI MATURITÀ
Ma cosa succede nel caso dovessimo prendere due corpi celesti con grandezze e
masse diverse?
Prendiamo, ad esempio, Giove e il Sole. Il Sole corrisponde a 1000 volte Giove.
Ora dividiamo il Sole in mille parti. Ogni parte del Sole attrarrà Giove con un’intensità
uguale a quella con cui Giove attrarrà quella parte del Sole verso di sé (come detto
prima, parti uguali di materia si attraggono con forze uguali e contrarie). Così per tutte le
1000 parti.
A questo punto è facile vedere, che le intensità delle forze reciproche sono uguali.
Ovviamente qualcosa di differente ci deve essere. Infatti le accelerazioni risultanti non
sono uguali. Entrambi i corpi si attraggono con la stessa intensità, ma il Sole, avendo
un’inerzia 1000 volte maggiore del pianeta, risponde a questa attrazione con
un’accelerazione solamente 1/1000 di quella alla quale risponde Giove.
4.6 Quattro regole del filosofare
Newton enuncia quattro regole del metodo scientifico.
Nel terzo libro dei Principia, Newton enuncia quattro «regole del ragionamento
“filosofico”. Queste regole si basano sul metodo scientifico e sono quelle che gli
permisero di estendere i risultati ottenuti in una piccola zona all’intero universo.
Vediamole qui di seguito:
Regola I: “La natura non fa nulla invano, ed è vano fare con mezzi maggiori ciò che
può essere fatto con pochi mezzi”. Questa frase spiega che la natura è semplice e non
bisogna porsi più domande di quelle che servono. Riflessioni del genere vengono fatte
da tempo da molti scienziati.
Regola II: “Perciò, finché è possibile, dobbiamo attribuire le medesime cause a effetti
naturali dello stesso genere. Come alla respirazione dell’uomo e dell’animale; alla caduta
delle piante in Europa e in America; alla riflessione della luce sulla Terra e sui pianeti”.
23
NEWTON
Regola III: “Le proprietà comuni a tutti gli oggetti che si trovano alla nostra portata
debbono essere attribuite (almeno a scopo di tentativo) a tutti i corpi in generale”.
Regola IV: “Nella «filosofia sperimentale» le ipotesi o le generalizzazioni basate
sull’esperienza debbono essere accettate come «esatte o assai vicine al vero, nonostante
qualsiasi ipotesi contraria che possa essere immaginata», finché non siano raccolte prove
ulteriori che possano giustificare le revisioni o i miglioramenti delle ipotesi iniziali”.
Grazie a queste regole riusciamo a capire come mai Newton abbia cercato di
ampliare la validità delle sue leggi a tutto l’universo.
4.7 La Luna e la forza gravitazionale
Sappiamo che se lanciamo una palla in alto ricade sulla Terra a causa del fatto che la
palla risente costantemente della forza attrattiva gravitazionale. Allo stesso modo per
Newton la Luna risentendo della forza di gravità è in caduta libera verso la Terra, come
una palla. Se si annullasse la forza di gravità, la Luna seguirebbe una traiettoria
tangenziale alla sua orbita perdendosi nello spazio, se invece si annullasse la sua
rivoluzione cadrebbe lungo la verticale sulla Terra.
Figura 13: Forza gravitazionale terrestre
24
GIULIA PINOJA – LAVORO DI MATURITÀ
Il punto di caduta di un corpo dipende dalla velocità iniziale del corpo stesso e
dall’altezza da cui è lanciato. Il motivo per cui la Luna non cade sulla Terra è che la
velocità iniziale della Luna e la sua altezza rispetto al suolo sono valori molto grandi
quindi il punto in cui dovrebbe cadere è distante, tanto distante da risultare ogni volta al
di là della Terra stessa. Istante per istante quindi la Luna si ritrova sempre nella stessa
situazione di caduta libera verso la Terra, ma non la raggiunge mai perché il punto in cui
dovrebbe cadere si trova costantemente fuori dalla superficie terrestre. Come si intuisce
bene dal disegno dunque, percorso un tratto di caduta libera la Luna si ritrova nella
stessa situazione di prima. È quindi un moto continuo che non si risolverà mai con uno
scontro della Luna con la Terra. Si dice, in termini tecnici, che Terra e Luna si trovano
in equilibrio. Newton si arrese davanti al problema di descrivere l’orbita della Luna
attorno alla Terra tenendo conto dell’influenza della gravità relativa al Sole. Si arrese
perché capì che non aveva il necessario strumento matematico che lui stesso aveva
inventato ma non ancora abbastanza sviluppato: “l’analisi matematica” . Lo strumento,
perfezionato qualche secolo dopo, permise lo studio delle perturbazioni che i vari
pianeti del Sistema Solare generano a vicenda modificando e complicando di molto i
calcoli delle orbite. Una delle prove che le leggi della fisica valgono tanto sulla Terra che
nell’universo e che consacrarono il trionfo della teoria della gravitazione fu proprio la
scoperta nel 1846 del pianeta Nettuno perché, a causa di una perturbazione
gravitazionale del pianeta Urano, si riuscì a calcolare l’orbita di Nettuno e quindi fu
facile puntare il telescopio su un punto di questa orbita.
4.8 Excursus sul perché la Luna non è sempre piena
Sizigia: in astronomia indica la situazione in cui tre o più corpi sono grosso modo
allineati su una linea retta. Ovviamente questo è osservabile se ci si trova su uno di
questi corpi e normalmente uno dei tre corpi presi in causa è la Terra.
Sappiamo che una fase lunare dura circa 28 giorni. In questo periodo abbiamo due
volte una sizigia, cioè ci troviamo due volte perfettamente allineati con il Sole e la Luna:
novilunio e plenilunio.
Figura 14: Sizigia lunari
25
NEWTON
Metà della Luna viene costantemente illuminata dal Sole, ma noi riusciamo a vedere
l’intera metà illuminata solo quando ci troviamo tra i due corpi celesti, in quel periodo si
dice che c’è “luna piena” o “plenilunio”. Dopodiché la parte di Luna illuminata va
diminuendo fino a tornare alla “luna nuova”, cioè al “novilunio”.
Figura 14: Fasi lunari
La Luna, nonostante la luce solare sia la stessa di quella che riceve la Terra, a
differenza di quest’ultima non ha un’atmosfera che filtra gran parte dei raggi solari
(quegli stessi che ci permettono di vederla nella notte), quindi la parte di superficie
illuminata può raggiungere anche i 100°C. Al contrario, dalla parte non illuminata, non
avendo atmosfera che trattiene calore, si può arrivare anche ad una temperatura di 150°C.
Il periodo migliore per osservarla è nel primo o nell’ultimo quarto di fase lunare,
cosicché sia visibile, ma il bagliore non sia troppo forte.
Essa non è visibile sempre al medesimo orario, infatti sorge ogni notte 50 minuti più
tardi.
26
GIULIA PINOJA – LAVORO DI MATURITÀ
5 Come sottrarsi all’attrazione terrestre
5.1 Velocità di fuga
La velocità di fuga è la velocità minima che un oggetto deve acquisire per riuscire ad
uscire dal campo di attrazione gravitazionale del pianeta sul quale si trova ed è
calcolabile utilizzando la legge di gravitazione universale di Newton.
L’attrazione tra un corpo di massa m sulla Terra e la Terra stessa ha una forza di
attrazione costante mg, g è chiamata intensità del campo gravitazionale. Se dovessimo
lanciare un oggetto in un qualsiasi campo gravitazionale ad una certa velocità v, questo
oggetto salirebbe fino ad una certa altezza che chiamiamo h. Il nostro oggetto
inizialmente, ponendo 0 il potenziale gravitazionale sulla terra, avrà energia potenziale
iniziale nulla mentre l’energia cinetica iniziale sarà 1/2m𝑣 ! . Al momento in cui il corpo
raggiungerà la quota massima l’energia cinetica sarà nulla, mentre quella potenziale sarà
mgh appunto per il principio della conservazione dell’energia:
1
mv ! = mgh ossia v ! = 2gh
2
banalmente si può capire che maggiore è la velocità iniziale, maggiore sarà l’altezza h
prima che il corpo abbia energia cinetica nulla. Se sulla terra si trovasse un campo
gravitazionale uniforme non sarebbe possibile trovare nessuna velocità di fuga, ma
grazie a Newton sappiamo che non è così, infatti il campo gravitazionale terrestre
diminuisce di 1/𝑟 ! con r raggio della terra. Infatti se volessimo calcolare esattamente la
quota massima raggiunta da un oggetto che parte da terra con una velocità molto
grande, di modo che percorra almeno una distanza equivalente al raggio terrestre,
dobbiamo tener conto della forza di gravità agente sul corpo. Quindi dobbiamo trovare
l’espressione corretta che tenga in considerazione questa diminuzione della forza del
campo gravitazionale di 1/r ! .
Ciò che ora vogliamo riuscire a stabilire è quanto necessita un corpo per alzarsi dalla
sua posizione iniziale sulla superficie terrestre. Il corpo parte a una distanza dal centro
della terra r! che è il raggio terrestre (RT) e la sua posizione finale sarà r, cioè h = r −
r! . Come abbiamo detto prima all’aumentare dell’altezza diminuirà la forza
gravitazionale, infatti inizialmente avremo una forza di GM! m/R!! e alla fine
GM! m/r ! . Trovando la forza media e moltiplicandola per la distanza (h) possiamo
trovare il lavoro che compie questo oggetto:
F!"#$% =
GM! m
rR ! quindi il lavoro W che deve essere effettuato per alzare questo oggetto è la forza media
per la distanza, quindi:
27
COME SOTTRARSI ALL’ATTRAZIONE TERRESTRE
W=
!!! !
!!! r − r! =
!!! !
!!
−
!!! !
!
Questo risultato è uguale all’energia potenziale (U) a distanza r:
U = !!! !
!!
−
!!! !
!
però è da tenere in considerazione che in un campo gravitazionale come il nostro, cioè
non uniforme, il grafico dell’energia potenziale non sarà una retta perché all’aumentare
di r il secondo termine dell’equazione sarà sempre più piccolo e quindi di conseguenza
!! !
l’energia potenziale tende a raggiungere un valore massimo U!"# = !! .
!
Ora passiamo al punto successivo, il quale ci permetterà di trovare la velocità iniziale
che dobbiamo dare all’oggetto di modo che possa sfuggire al campo gravitazionale
terrestre.
Teniamo a mente che l’energia potenziale non può oltrepassare il nostro valore U!"#
quindi raggiunto questo valore abbiamo l’energia cinetica minima, che oltre non può
diminuire (sappiamo che se aumenta la potenziale diminuisce la cinetica, ma dal
momento che la potenziale non può più aumentare la cinetica non può più diminuire).
Quindi ovviamente se si dovesse dare inizialmente un’energia cinetica maggiore
dell’energia massima potenziale, il corpo non arriverebbe mai ad un punto in cui si
ferma avendo energia cinetica nulla, di conseguenza potrebbe andare avanti con
un’energia infinta e lasciare il campo gravitazionale.
Ricapitolando: per fare in modo che un corpo possa lasciare il nostro campo
gravitazionale è sufficiente che in partenza disponga di un’energia cinetica maggiore
!! !
dell’energia massima potenziale che può raggiungere cioè !! .
!
Come già citato prima esiste la velocità di fuga, proprio quella velocità che ci
permette di lasciare il nostro campo gravitazionale, ovviamente in relazione ai calcoli
appena fatti e ora cerchiamo di scoprire quanto è:
!
mv!! = U!"# =
!
!!! !
ossia
!! v! =
!!!!
!! siamo giunti quasi alla conclusione, basta sostituire GM! con gR!! e inserendo i dati che
già conosciamo come g = 9,81 m/s ! e R ! = 6,37 Mm, ottenendo così:
v! =
2GM!
=
R ! 2gR ! =
2(9,81
m
)(6,37 ∙ 10! m) = 𝟏𝟏, 𝟐 𝐤𝐦/𝐬
s!
La velocità di fuga è possibile calcolarla per qualsiasi pianeta, basta cambiare g con la
rispettiva accelerazione di gravitazione e R ! con il rispettivo raggio del pianeta.
28
GIULIA PINOJA – LAVORO DI MATURITÀ
6 Comete
6.1 Da dove arrivano
Le comete sono presenti da più di 4,6 miliardi di anni, vale a dire da quando il Sole e i
pianeti hanno cominciato la loro formazione; infatti questi composti di blocchi di
ghiaccio e polvere sono le componenti più antiche e meno alterate del nostro Sistema
Solare.
Le comete provengono da due zone principali. La prima è chiamata fascia di Kuiper,
Figura 15: Sistema solare, fascia di Kuiper
una zona dello spazio sullo stesso piano orbitale dei pianeti del Sistema Solare, posta
nelle vicinanze del nostro Sistema, oltre Plutone. Queste sono in genere le comete di
breve e medio periodo, cioè quelle più frequenti. La seconda zona è chiamata zona di
Oort, una nube che circonda tutto il Sistema Solare, dove si trovano le comete a più
lungo periodo. Quelle che in genere vediamo noi, sono quelle di medio e breve periodo.
Si presume che le comete siano residui dalla condensazione della nebulosa che formò il
Sistema Solare. La composizione di tutte le comete che orbitano attorno al nostro
sistema formano la nube di Oort, composta da trilioni di comete, ipotizzata appunto da
Jan Oort. In questa nube gli urti sono rari, infatti la nube di Oort è molto più grande del
Sistema Solare stesso. Nonostante la maggior parte delle comete orbiti in questa nube,
alcune non ne fanno parte, altrimenti sarebbe impossibile per noi umani vederle, perché
la luce solare riflessa da esse sarebbe comunque troppo bassa per essere vista dai nostri
telescopi. Infatti a volte avvengono delle deviazioni facendo diventare queste comete
delle vagabonde stellari oppure possono semplicemente essere dirette per sbaglio nel
Sistema Solare intero. Quelle che arrivano dentro nel nostro sistema hanno due
possibilità: o passano solamente una volta attorno al Sole, dopodiché escono
nuovamente dal sistema, oppure si stabilizzano su un’orbita attorno al Sole, molto più
piccola rispetto a quella precedente e portandole più vicine a noi, catturata dalla forza
gravitazionale dei pianeti, principalmente di Giove essendo il pianeta più grande e
pesante. Infatti tutte le comete che conosciamo sono state catturate in questo modo,
compresa Halley, la cometa più famosa mai scoperta.
29
COMETE
6.2 Composizione
6.2.1 Composizione del nucleo
Le comete sono di svariate misure, relativamente piccole. Possono avere un nucleo
variabile da 100 metri a più di 50 chilometri. Questo nucleo è composto da roccia,
polvere, ghiaccio d’acqua e altre sostanze tra le quali molti gas presenti anche sulla Terra
(ad esempio: anidride carbonica, metano, monossido di carbonio e ammoniaca).
Generalmente quando si pensa ad una cometa si pensa a qualcosa di tremendamente
luminoso. Al contrario, le comete sono molto scure, praticamente nere, e riflettono
solamente dal 2 al 4% della luce con cui vengono illuminate, per rendere meglio l’idea
l’asfalto riflette il 7%.
6.2.2 Composizione della chioma
Cometa in greco significa ‘dotato di chioma’. Infatti, come tutti ben sappiamo, le
stelle comete hanno la particolarità di avere una lunga chioma “posteriore”. A differenza
delle ridotte misure del nucleo della cometa, la coda è estremamente grande, infatti nel
2007 è stata stimata in 1,4 milioni di chilometri la lunghezza della chioma della cometa
Holmes.
Come abbiamo già detto, la cometa è costituita prevalentemente da ghiaccio. Ma, dal
momento in cui entra nel Sistema Solare interno, il calore del Sole fa sciogliere lo strato
esterno di questo ghiaccio. Queste polveri e gas provocano un’atmosfera tutt’attorno al
nucleo. Quindi in teoria noi dovremmo vedere una coda a 360°. Ovviamente non è così.
Questo perché noi possiamo vedere solo la parte illuminata dal Sole, quindi la parte
che si trova non tra il Sole e la cometa ma dietro la cometa. Questo può sembrare strano
per il fatto che se la cometa si sta dirigendo lontano dal Sole, la sua chioma è situata
davanti alla cometa stessa.
Figura 16: Chiome di una cometa
Come possiamo vedere nel disegno, la coda si situa sempre dalla parte opposta del
Sole. Nel disegno si nota anche che la cometa dispone di due code. Infatti può capitare
che polveri di ghiaccio e gas formino due code distinte. La polvere può rimanere più
indietro rispetto al nucleo formando così una chioma leggermente incurvata che si
30
GIULIA PINOJA – LAVORO DI MATURITÀ
mantiene sull’orbita. Mentre il gas, più sensibile al vento solare, forma una chioma dritta,
sempre opposta al Sole, seguendo non più la traiettoria orbitale ma il campo magnetico.
Queste, nonostante la loro grandezza, restano comunque molto sottili, tanto che è
possibile vedere le stelle attraverso di esse.
6.3 Movimento orbitale di una cometa
Quando le comete si trovano nel Sistema Solare esterno restano in uno stato
congelato e a causa delle loro piccole dimensioni è quasi impossibile avvistarle dalla
Terra. Le loro orbite sono immense e si estendono oltre quella di Plutone. Le comete
che riusciamo a vedere sono quelle che sono entrate nel Sistema Solare interno.
Normalmente le comete ruotano su orbite ellittiche molto allungate, cioè con una forte
eccentricità. Queste orbite le portano per un breve periodo molto vicine al Sole, e in
quel momento sono visibili dalla Terra.
Usualmente vengono suddivise in base al loro periodo orbitale:
Le Comete di corto periodo corrispondono alle comete che hanno un periodo
inferiore a 200 anni e hanno un’ orbita con bassa eccentricità.
Le Comete di lungo periodo normalmente hanno eccentricità elevata e hanno un
periodo che può variare da 200 anni a anche miglia o milioni di anni.
Le Comete extrasolari (in inglese vengono chiamate Single-apparition comets, cioè
comete da una singola apparizione). Normalmente la loro orbita è una parabola o
un’iperbole, quindi come possiamo immaginare, passano solo una volta davanti al sole
dopodiché escono per sempre dal nostro sistema.
6.4 Acqua grazie alle comete
Come arrivò l’acqua sul nostro pianeta? Ci sono diverse teorie per spiegarlo.
Una recente teoria, sostiene che una grande percentuale dell’acqua presente sulla
Terra possa avere origini spaziali (origini esogene). Più specificatamente una piccola
parte potrebbe avere avuto origine dalle comete. Come vedremo più avanti, sappiamo
che il nucleo delle comete è composto da una grande quantità d’acqua. Basterebbe che
14.000 comete come quella Hale-Bopp si impattassero con la Terra, per avere già metà
dell’acqua che è presente oggi sul nostro pianeta.
Ovviamente non tutti condividono pienamente questa teoria. C’è infatti chi sostiene
che la composizione dell’acqua delle meteore sia diversa da quella degli oceani.
Infine è stata avanzata una terza ipotesi, a seguito delle scoperte effettuate dal satellite
artificiale chiamato Polar. Questo satellite ha scoperto alcuni piccoli corpi ghiacciati che
passano attraverso l’atmosfera, i quali si disintegrano ad una certa altezza causando delle
grandissime nubi d’acqua che in seguito si trasformano in piogge. Ma se così fosse,
l’acqua sarebbe in continuo aumento. In realtà, nonostante migliaia di questi
bombardamenti, la percentuale d’acqua nei mari resta costante, perché quest’aggiunta
serve solo da compensazione. Infatti ogni anno migliaia di tonnellate d’acqua affondano
nel mantello terrestre e non riescono a tornare in superficie.
31
COMETE
6.5 Le comete radenti di Kreutz
Comete radenti: queste comete sono quelle che passano al perielio (punto minimo di
distanza dal Sole, a cui può arrivare un corpo celeste, detto anche apside). Ad alcune di
queste, le più piccole, può capitare che ad un certo punto il calore del Sole le faccia
evaporare. Quelle più grandi invece normalmente non evaporano ma vengono
disintegrate.
Le comete di Kreutz sono comete radianti di questo tipo, che si avvicinano
estremamente al Sole. Si scoprì che probabilmente questa categoria di comete trae
origine comunque da un’unica grande cometa. Alcune di queste, in determinati periodi
vicini al Sole, sono visibili.
6.6 Morte delle comete
La vita cometaria è molto breve. La morte può essere causata da due fattori. Il primo
è dovuto al fatto che continuando a passare davanti al sole, infatti l’avvicinarsi al sole
non provoca solo la cattura orbitale ma quando questa cometa raggiunge una distanza
dal sole uguale a un paio di volte quella dalla terra al sole, il calore emanante dal Sole fa
sciogliere alcuni dei ghiacci cometari, dopodiché i gas e le polveri si diffondono attorno
alla cometa stessa formando la sua chioma questo procedimento si ripete ogni volta che
la cometa passa vicino al sole quindi per esse la vita non può durare più di qualche
milione di anni dopodiché tutta la loro parte composta da ghiaccio evapora. Così resta
solo la parte rocciosa, il nucleo della nostra cometa si trasforma in un asteroide. La
seconda possibilità è dovuta ad un legame della cometa con se stessa troppo lieve che
rischia di sparire all’interno di una nuvola di polvere.
A volte però invece di morire vengono semplicemente frammentate, queste
frammentazioni hanno normalmente origine da urti con piccoli asteroidi.
6.7 La cometa di Halley
Edmond Halley, scienziato, navigatore e astronomo, il quale convinse Newton a
pubblicare il suo libro i Principia. Egli prese tutti gli annunci che parlavano di comete e
notò che tali articoli distanziavano tutti a grosso modo con una distanza di 77 anni. Egli
quindi suppose che si trattasse di una sola cometa, con un’orbita molto molto grande e
facendo qualche calcolo ipotizzò che sarebbe comparsa nuovamente nel 1758. Causa
alcune perturbazioni gravitazionali causate da Giove e Saturno, la cometa ritardò, ma
comunque effettivamente passò, purtroppo il grande astronomo era già morto e alla
cometa fu dato proprio il suo nome dovutogli dalla sua grande ipotesi.
Oggigiorno sappiamo circa la grandezza della sua orbita: ha l’afelio che dista da
Nettuno 33 volte la distanza Terra-Sole e il perielio metà della distanza dell’afelio.
Nel 1986 è stata scoperta la grandezza di questa cometa, la quale equivale a 15km x
8km x 8km ed è a forma di cetriolo, rivestita da composti con alta quantità di carbonio
da un colore molto scuro alla cometa.
32
GIULIA PINOJA – LAVORO DI MATURITÀ
6.8 Molto di più
Negli ultimi anni molti scienziati hanno supposto che 26 milioni di anni fa una
quantità immensa di comete abbia deviato dalla nube di Oort, con la conseguenza che
l’interno del nostro sistema solare sia invaso da uno sciame di comete. È possibile infatti
che alcune di queste comete colpiscano il nostro pianeta. Il risultato di una cometa larga
10km che colpisce la terra sarebbe un enorme cratere e una nube immensa che si
innalzerebbe nella nostra atmosfera. Probabilmente nei mesi a seguire, nei quali le
polveri stanno ancora cadendo adagio adagio sul suolo terrestre, queste polveri non
permetterebbero più come oggi ai raggi solari di entrare, la terra si raffredderebbe,
sarebbe molto più scuro e le condizioni peggiori verrebbero subite dai posti lontani dai
mari dal momento che l’acqua immagazzina calore.
Questa potrebbe essere una motivazione della scomparsa dei dinosauri. Infatti è stato
dimostrato che strati di roccia che si sono depositati all’incirca quell’epoca sono
composti da sostanze che normalmente si possono trovare solo quasi al centro della
terra, come l’iridio, un’ipotesi è appunto quella che queste sostanze si trovino in
superficie a causa di un urto di qualcosa che ha colpito la terra con le dimensioni di circa
10/20 km, e una cometa casualmente è composta proprio di queste alte quantità di
iridio.
A questo punto è facile collegare che nel momento in cui la Terra è stata colpita dalla
cometa, per i giganteschi rettili è stata dura sopravvivere, mentre per i mammiferi è stato
più semplice, permettendoli di riuscire a cavarsela ed in seguito di evolversi fino ad
arrivare a noi. Questa è chiamata teoria meteorica. Dopodiché arriva anche la teoria
ciclica che pone che questi urti vengano ripetuti ogni 26 milioni di anni con la
deviazione di massa dalla nube di Oort e quindi ogni 26 milioni di anni si verificano
estinzioni di massa. Ma ci sono ancora molte discussioni a riguardo.
33
COMETE
6.9 Altri corpi minori
6.9.1 Corpi minori
I corpi minori sono corpi che appartengono sempre al sistema solare ma che sono
più piccoli e hanno rilevanza inferiore rispetto ai pianeti o al sole.
Questi corpi minori si ipotizzi possano essere resti che rappresentino la primordiale
materia proto-planetaria indifferenziata.
Le orbite di questi corpi a volte li porta ad avvicinarsi pericolosamente al nostro
pianeta.
Delle comete abbiamo già parlato, ora facciamo qualche accenno veloce sugli
asteroidi e i meteoriti.
6.9.2 Asteroidi
L’asteroide è considerato un corpo celeste, la sua composizione è simile a quella di
un corpo terrestre, ma non ha una forma sferica, anzi del tutto astratta.
La maggior parte degli asteroidi si trova nella fascia principale, cioè la fascia situata
tra le orbite di Marte e di Giove, alcuni di questi asteroidi dispongono di asteroidi
secondari che fanno da satelliti.
La loro orbita è molto eccentrica.
Gli asteroidi sono composti da minerali rocciosi e da ferro. Si è pensato che siano un
residuo della materia primordiale dato che gli asteroidi vicino a Giove sono scuri e
rossastri e dispongono di una composizione non molto differente da quella della
nebulosa primordiale.
Alle origini si pensa che i corpi solidi si aggregarono per formare i pianeti, oltre
Marte, causa le risonanze gravitazionali ( risonanze gravitazionali: Cioè quando il
rapporto dei periodi di rotazione di due corpi si può esprimere in frazioni di numeri
interi piccoli. Viene esercitata da ogni corpo una regolare influenza gravitazionale
sull’altro. Questo fenomeno stabilizza le orbite e le protegge da perturbazioni
gravitazionali) di Giove non fu permessa la formazione di corpi con un diametro che
superava 1000 km. Quindi i pezzi che non si aggregarono divennero quelli che noi oggi
chiamiamo asteroidi.
L’asteroide più grande del sistema solare interno si chiama Cerere con diametro di
900-1000km
Come abbiamo già detto la maggior parte degli asteroidi orbita nella fascia tra Marte
e Giove. Le perturbazioni gravitazionali emanate da Giove hanno creato le lacune di
KirKwood, delle zone nelle quali gli asteroidi non possono entrare perché andrebbero
incontro a delle risonanze orbitali con Giove e verrebbero espulsi.
34
GIULIA PINOJA – LAVORO DI MATURITÀ
Asteroidi troiani:
Questi asteroidi hanno un’orbita molto simile a quella di Giove. Con troiano si
intende un asteroide che ha la stessa orbita di un pianeta, ma non collide con esso dato
che orbita intorno a uno dei due punti la Lagrange di stabilità L4 e L5, che si situano 60°
davanti o dietro al corpo celeste. Nel nostro caso il pianeta naturalmente è Giove.
Asteroidi Centauri:
Orbitano attorno al sole in mezzo ai pianeti giganti (oltre l’orbita di Giove). Si pensa
che un tempo questi asteroidi appartenessero ad orbite dalle quali in seguito sono state
espulse ed immesse in orbite che seguono traiettorie in regioni molto meno popolate dai
comuni asteroidi.
Classificazione:
Asteroidi di tipo C: rappresentano il 75% degli asteroidi conosciuti. La C significa
"carbonacei". Sono molto scuri e assomigliano alle meteoriti carbonacee. La
composizione di questi asteroidi è quasi la stessa del Sole, tranne per l'idrogeno, l'elio e
altri elementi volatili. I loro spettri hanno colori tendenti al blu, sono piatti e senza
strutture evidenti.
Asteroidi di tipo S: rappresentano il 17% degli asteroidi conosciuti. La S significa
"silicio". Sono corpi abbastanza luminosi. La loro composizione è metallica
(principalmente composti da silicati di nichel, ferro e magnesio). Lo spettro di questi
asteroidi tende fortemente al rosso ed assomiglia alle meteoriti ferrose.
Asteroidi di tipo M: rappresentano quasi tutti gli asteroidi rimanenti. La M vuole
significare "metallico". Sono asteroidi abbastanza brillanti e sembrano fatti di nichelferro quasi puro.
Figura 17: Asteroide
35
COMETE
6.9.3 Meteorite
Un piccolo asteroide è anche chiamato meteoroide. Con l’ablazione di quest’ultimo
(Ablazione definisce il processo dove viene rimosso del materiale mediante processi di
vaporizzazione ed erosione da un oggetto) il meteoroide si trasforma in una meteorite,
questo avviene quando esso entra in collisione con la Terra.
Quando questi meteoroidi entrano nell’atmosfera si riscaldano e emettono una luce
lasciando una scia luminosa che viene comunemente chiamata o meteora o stella
cadente.
Impatto con la superficie terrestre:
sono rari gli impatti con la superficie terrestre (circa 500 all’anno, di cui solo 5/6
vengono trovate), perché la maggior parte di essi si disintegrano in aria.
Le meteoriti che colpiscono la terra possono formare crateri di varia misura, in
passato grandi meteoriti hanno causato anche diversi disastri.
Suddivisione:
i meteoriti possono essere rocciosi (composto prevalentemente da silicati), ferrosi
(composto prevalentemente da ferro e nichel) o ferro-rocciose (composte sia da metallo
che roccia). A dipendenza delle tre categorie possono cambiare alcune caratteristiche.
Ma normalmente, indipendentemente dal tipo, le meteoriti appena cadute dispongono di
una crosta di fusione scura e di piccole cavità chiamate regmagliti. La loro forma non è
mai sferica.
Figura 18: Meteorite ferrosa
Figura 19: Meteorite rocciosa
36
GIULIA PINOJA – LAVORO DI MATURITÀ
7 Esplorazione del sistema solare
7.1 Dall’antichità ad oggi
7.1.1 In passato
Già presso aztechi, cinesi, arabi, antichi greci e popoli della Mesopotamia le stelle
furono fonte di grande interesse, ricerca e osservazione. Principalmente questi popoli si
affidavano alla posizione stellare per tenere il conto dei giorni in un calendario preciso.
Due furono gli astronomi dell’antichità, i già citati Tolomeo e Aristarco. Purtroppo
l’unico mezzo d’osservazione di cui disponevano era la propria vista ad occhio nudo.
Nel 1608 il produttore di lenti olandese Hans Lippershey fece un grande passo avanti
negli strumenti d’osservazione astronomici, costruendo il primo telescopio. Dopodiché
Galileo Galilei, grazie a questo strumento innovativo, riuscì a ipotizzare un Sistema
Solare eliocentrico, scoprì le macchie solari e i satelliti di Giove.
Ovviamente l’uomo non si accontenta mai, non era più sufficiente aver capito la
struttura e il funzionamento del sistema solare, ora bisognava anche esplorarlo. Ci sono
svariati motivi per i quali si è cominciato ad esplorare lo spazio. I principali sicuramente
sono la rivalità internazionale, la voglia di esplorazione dell’ignoto e il possibile
progresso scientifico.
La corsa all’esplorazione dello spazio cominciò attorno agli anni ‘50 del secolo
precedente, detto anche “prima era spaziale”. I principali protagonisti furono gli USA e
l’URSS, i quali si sfidarono durante la guerra fredda, cercando di conseguire sempre più
successi e scoperte spaziali.
Oggi le spedizioni spaziali di navicelle non sono più prevalentemente finalizzate a
scopi militari, strategici o di prestigio, ma principalmente a scopi astronomici, di
controllo del territorio, medici, telecomunicativi e di studio del Sistema Solare.
Negli anni, la continua competizione tra nazioni fornì la spinta necessaria a costruire
missili che vennero lanciati a qualche centinaio di km al di sopra della Terra. I primi
furono i missili V2, costruiti dallo scienziato Wernher Von Braun durante la seconda
guerra mondiale.
In seguito l’Unione Sovietica nel 1957 lanciò il primo oggetto in orbita attorno alla
Terra, che però dopo 21 giorni si incendiò.
In novembre dello stesso anno venne effettuato nello spazio un altro volo con a
bordo la famosa cagnetta Laika, ma già dall’inizio non era previsto il rientro orbitale
della capsula.
Nel 1959 si colloca la prima esplorazione lunare con l’allunaggio di una sonda
sovietica. Da allora cominciò un decennio di continue spedizioni lunari. Nel 1964 i
sovietici riuscirono a far rientrare una navicella con a bordo animali, mentre solo gli
USA fecero spedizioni umane.
37
ESPLORAZIONE DEL SISTEMA SOLARE
One small step for [a] man, one giant leap for mankind1.
Questa fu la celebre frase che pronunciò Neil Armstrong, conosciuto come il primo
uomo che mise piede sulla Luna, il 20 luglio del 1969; fu una grande soddisfazione per
gli Stati Uniti d’America.
In compenso la Russia fu la prima a creare una stazione spaziale orbitante.
In seguito fu quasi infinito il numero di sonde, astronavi e navicelle spaziali che
vennero mandate nello spazio sulla Luna e su altri corpi celesti.
I pianeti esplorati finora sono la Luna, Venere e Marte. Altri corpi celesti per il
momento sarebbero troppo difficili da esplorare, sia per la lontananza, sia per la
temperatura e anche per la loro struttura, come, ad esempio, Giove, uno dei giganti
gassosi, senza una superficie ben definita. In più si riuscì anche a far impattare sonde su
alcune comete, riportandone del materiale a Terra.
Causa gli elevati costi, solo 4 sono le sonde lanciate tutt’oggi fuori dal Sistema Solare.
7.1.2 Attualmente
Nel nostro secolo uno dei principali obiettivi nell’esplorazione lunare, ha dichiarato il
cosmochimico Ouyang Ziyuan, è quello di ricavare una fonte di elio-3, dal quale
ottenere del combustibile trasformabile in energia. L’agenzia spaziale russa ha
annunciato che in teoria si dovrebbe riuscire ad estrarre questo elio-3 entro il 2020.
In orbita terrestre bassa è stata installata una stazione spaziale, la quale permette
all’uomo di essere continuamente presente nello spazio.
Al momento si sta studiando, dalle immagini che riceviamo in diretta della superficie
di Marte, la possibile vita marziana passata e presente.
Allo stesso tempo è stata mandata una sonda in direzione di Plutone, ma quest’ultima
deve ancora arrivare a destinazione.
Entro il 2020 è previsto lo sbarco umano su Marte.
1
Neil Armstrong, nel discendere la scaletta del Modulo Lunare dopo l’allunaggio, 20 luglio 1969.
38
GIULIA PINOJA – LAVORO DI MATURITÀ
7.2 Parte per parte
7.2.1 Introduzione
Guardando più nello specifico l’attività spaziale, si possono notare due strade ben
distinte: una riguarda la missilistica e l’altra riguarda l’esplorazione spaziale. Nonostante
questo però, la seconda necessita della prima. Inoltre possiamo ancora suddividere
l’esplorazione spaziale in due categorie: esplorazione tramite satelliti artificiali o
mediante sonde spaziali.
7.2.2 I razzi
I razzi hanno origine in Cina, nell’XI secolo. Inizialmente furono inventati a scopi
militari. Gli studi storici ci dicono che il razzo è arrivato in Europa solo nel XIII-XV
secolo, a scopo bellico. Ma il suo uso non fu di grande successo, fino a quando venne
riutilizzato nel XVIII-XIX secolo a scopi militari.
Dopo la prima guerra mondiale il razzo acquistò sempre maggiore importanza e fu
oggetto di sempre maggior studio. Infatti nel 1928 si pensò di applicare la propulsione a
razzo alle automobili ed in seguito anche agli aeroplani. In seguito queste idee non
funzionarono, a causa dell’elevata potenza di un razzo, ingestibile in un autoveicolo.
Fu però nel 1929 che la missilistica ebbe il suo momento di gloria. La Germania
infatti, in una località vicina a Berlino (Kummersdorf), cominciò a produrre sempre più
missili, dato che questi non figuravano come armi vietate dal trattato di pace. Qui il non
ancora laureato W. von Braun studiò i razzi “a flusso continuo” (a liquido), contrapposti
a quelli “a polvere” (a solido). Questi razzi, con la sigla A (Aggregat) in seguito ebbero
un enorme successo. Anche se il modello A3 fu un vero fallimento, sostituito in seguito
con il modello A5, precursore del V2 (A4).
Il primo volo del V2 venne effettuato con successo nel 1942 e ottenne i seguenti
risultati: velocità massima 1.500 m/s, distanza di lancio 200 km e altezza 90 km. In fine
tenuto verticalmente riusciva a raggiungere una gittata massima di 320 km e un’altitudine
di 200.
Nello stesso tempo, nella stessa base spostata a Peenemünde (sul Baltico), venne
creata una bomba volante, l’F 103, chiamata in seguito anche V1 (Vergeltungswaffe 1=
arma di rappresaglia 1). Questa venne finita di perfezionare nel 1944 e nello stesso anno
ne vennero lanciate alcune su Londra. In seguito, l’anno successivo, vennero lanciati
anche i V2 (detti anche A4). Allora i tedeschi, vedendo gli ottimi risultati, decisero di
continuare nel perfezionamento dei razzi, ma per fortuna gli ultimi prototipi non
vennero mai lanciati. Nonostante tutto, prima della resa, i tedeschi riuscirono a far
scomparire quasi completamente la loro base missilistica, facendo trovare ai sovietici nel
maggio del 1945 pochissime attrezzature e un quarto dei tecnici.
Gli Stati Uniti erano nettamente indietro nella missilistica rispetto alla Germania.
Solo nel 1947, infatti, venne realizzato il primo razzo utilizzabile. A differenza dei
tedeschi, lo scopo di questi razzi era prettamente scientifico, più precisamente erano
utilizzati come sonde per ottenere informazioni sulle grandezze fisiche dell’alta
atmosfera. In seguito anche gli americani cominciarono ad usali in operazioni militari.
39
ESPLORAZIONE DEL SISTEMA SOLARE
Pochi anni dopo venne fondata la NASA e da allora in poi gli Stati Uniti d’America si
trovarono sempre all’avanguardia nell’esplorazione dello spazio.
7.2.3 I missili
I veicoli di lancio, più comunemente chiamati ‘missili’, sono tra gli oggetti lanciati
nello spazio, quelli che contribuiscono maggiormente ai progressi nell’esplorazione dello
spazio stesso.
Il loro compito è di tipo prevalentemente meccanico, in particolare, servono ad
imprimere ad un carico che si trova inizialmente a riposo sulla nostra superficie (punto
A) una spinta sufficiente a fargli raggiungere una determinata velocità (detta v) in
direzione di un determinato punto (detto B). Il missile deve possedere organi di
propulsione, di guida e di controllo, appunto perché deve riuscire a portare il carico
esattamente da un punto A ad un punto B. Questi sistemi di propulsione utilizzano il
principio di reazione.
Il motore a reazione è un motore capace di trasformare l’energia chimica del
combustibile in energia cinetica così da utilizzare il principio di azione reazione esteso.
Questo principio, detto anche terzo principio della dinamica classica, impone che per
ogni forza che un corpo esercita su un altro ne esiste un’altra uguale ma inversa. Infatti
nel caso del missile la spinta di reazione che causa il movimento è in proporzione con i
gas in massa che passano nel motore e alla differenza tra la velocità di scarico e quella di
avanzamento dell’aereo. Quanto appena detto comprende propulsori a turbogetto, a
turboventola, ecc. e proprio quelli ai quali siamo interessati noi: a razzo.
Il sistema a propulsione tradizionale utilizzato per i razzi spediti nello spazio è
composto da razzi chimici con i quali è possibile manovrare, accelerare o decelerare il
veicolo.
Una variante a questi propulsori sono quelli ionici, cioè con motori elettromagnetici.
Normalmente i missili sono sinonimi di razzo anche se una differenza tra i due può
essere che il missile ha un sistema guidato mentre il razzo no.
I missili vengono usati principalmente in guerra.
I missili balistici sono quelli che stanno gran parte del loro tragitto in aria senza
spinta e che non usano la variazione aereodinamica per cambiare rotta.
La gamma dei missili è molto vasta, ai giorni d’oggi disponiamo dei ICBM che
corrispondo ai più grandi missili mai sviluppati e sono l’arma più distruttiva al mondo
mai creata prima.
40
GIULIA PINOJA – LAVORO DI MATURITÀ
7.2.4 I satelliti
Lo Sputnik1 fu la prima sonda che i sovietici misero in orbita, nel 1957. Anche qui
all’inizio i sovietici si dimostrarono superiori a tutte le altre nazioni. Questa sonda
permise di misurare per 21 giorni le proprietà fisiche dell’atmosfera. Senza perder
tempo, i sovietici lanciarono subito lo Sputnik 2 con a bordo la cagnetta Laika. Nel 1958
anche gli Stati Uniti lanciarono il loro primo satellite, l’Explorer 1, che fu molto più
avanzato rispetto a quelli sovietici.
Il periodo di rotazione di un satellite artificiale:
Oggigiorno attorno alla Terra ruotano tantissimi satelliti artificiali, alcuni di essi
seguono orbite circolari e con i calcoli visti in precedenza è possibile calcolare il loro
periodo di rotazione.
Indichiamo con R il raggio, cioè distanza CentroSatellite-CentroTerra mettiamo in
relazione l’uguaglianza:
M! m!
4π!
G ! = m! ! R !"
T
R !" con m! che indica la massa del satellite quindi:
T! =
!!! !!!"
!!!
ossia
T = 2π
!!!"
!!!
supponendo ora che la distanza dalla terra sia di 500km otterremmo:
T = 2π
1
(!,!∙!"! !)!
!,!"∙!"!! !!! /!"! !∙!"!"!"
Tradotto : Compagno di viaggio.
41
= 5,69 ∙ 10! s ≅ 95 minuti
CONCLUSIONE
8 Conclusione
Con questi molteplici esempi di missili, razzi ed esplorazioni spaziali varie voglio solo
mostrare dove l’essere umano, noi, siamo riusciti ad arrivare oggi. Tutto ciò che adesso
sappiamo, conosciamo e vediamo riguardo non solo allo spazio, ma anche il nostro
pianeta, è partito da delle semplici supposizioni ed osservazioni ad occhio nudo. È
partito tutto dalla buona volontà di osservare e annotare dati empirici per giorni e per
anni.
Siamo partiti da Aristotele con ideali riguardo a un sistema geocentrico, abbiamo
visto come le idee delle persone con il tempo sono cambiate e si sono avanzate nuove
ipotesi, fino ad arrivare alla conclusione di un sistema eliocentrico. Grazie a questo, oggi,
sappiamo dove viviamo, cosa ci circonda ed infine il funzionamento del Sistema Solare.
Spero che questo lavoro di maturità sia stato di vostro gradimento e abbia risposto non
solo ad alcune mie curiosità, ma anche alle vostre.
Vorrei ringraziare inoltre il professore di italiano Alberto Mariatti per aver corretto e
reso comprensibile l’italiano con cui questo lavoro di maturità è stato scritto.
42
GIULIA PINOJA – LAVORO DI MATURITÀ
9 Sitografia/Bibliogragia
Astronomia. Teoria eliocentrica. astronomia.com (consultato il giorno 4. 12 2014).
Blog. Aristotele. blog.you-ng.it (consultato il giorno 4. 12 2014).
Digilander. Rivoluzione copernicana. digilander.libero.it (consultato il giorno 4. 12 2014).
eBook. Moto circolare uniforme. ebook.scuola.zanichelli.it (consultato il giorno 4. 12 2014).
Fmboschetto. Campo gravitazionale. fmboschetto.it (consultato il giorno 4. 12 2014).
Isgailei. La terra nello spazio. lsgalilei.org (consultato il giorno 4. 12 2014).
Matefilia. Modelli geocentrici. matefilia.it (consultato il giorno 4. 12 2014).
Osservareilcielo. Luna. osservareilcielo.altervista.org (consultato il giorno 4. 12 2014).
Parados. Sistema aristotelico-tolemaico. parodos.it (consultato il giorno 4. 12 2014).
Progetto fisica, volume 1. Zanichelli.
Scientifico. Leggi di Keplero. scientifico.asti.it (consultato il giorno 4. 12 2014).
Scienzapertutti. Orbita ellittica. scienzapertutti.lnf.infn.it (consultato il giorno 4. 12 2014).
Tanogabo. Copernico. tanogabo.it (consultato il giorno 4. 12 2014).
Torredelsole. Comete. torredelsole.wordpress.com (consultato il giorno 4. 12 2014).
Treccani. Eccentrico - Astronomia. treccani.it (consultato il giorno 4. 12 2014).
—. Esplorazione dello spazio. treccani.it (consultato il giorno 4. 12 2014).
Wellen. Astronomia. wellentheorie.wordpress.com (consultato il giorno 4. 12 2014).
Wikipedia. Asteroide. it.wikipedia.org (consultato il giorno 21. 1 2015).
—. Claudio Tolomeo. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Cometa. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Corsa allo spazio. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Eplorazione spaziale. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Equante. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Galassia. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Galileo Galilei. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Giovanni Keplero. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Immagine asteroide. http://it.wikipedia.org (consultato il giorno 21. 1 2015).
—. Immagine meteorite ferrosa. http://it.wikipedia.org (consultato il giorno 21. 1 2015).
—. Immagine meteorite rocciosa. http://upload.wikimedia.org (consultato il giorno 21. 1
2015).
—. Impulso angolare. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Isaac Newton. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Legge delle aree. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Legge di gravitazione universale. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Meteorite . http://it.wikipedia.org/wiki (consultato il giorno 21. 1 2015).
—. Missile. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Motore a reazione. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Neil Armstrong. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Principi della dinamica. it.wikipedia.org (consultato il giorno 4. 12 2014).
—. Propulsione. it.wikipedia.org (consultato il giorno 4. 12 2014).
43
INDICE DELLE FIGURE
10 Indice delle figure
Figura 1: Ritratto di Aristotele .................................................................................................... 5
Figura 2: Ritratto di Tolomeo II Filadelfo ................................................................................ 6
Figura 3: Sistema tolemaico-aristotelico.................................................................................... 6
Figura 4: Ritratto di Niccolò Copernico ................................................................................... 7
Figura 5: Sistema eliocentrico ..................................................................................................... 7
Figura 6: Ritratto di Galileo Galilei ............................................................................................ 8
Figura 7: Sistema di Brahe ........................................................................................................... 9
Figura 8: Ritratto di Giovanni Keplero ................................................................................... 10
Figura 9: Sezione conica ............................................................................................................ 12
Figura 10: Ellissi.......................................................................................................................... 13
Figura 11: Legge delle aree ........................................................................................................ 14
Figura 12: Forza circolare di una galassia ............................................................................... 19
Figura 13: Forza gravitazionale terrestre ................................................................................. 24
Figura 14: Sigizia lunari .............................................................................................................. 25
Figura 15: Fasi lunari .................................................................................................................. 26
Figura 16: Sistema solare, fascia di Kuiper ............................................................................. 29
Figura 17: Chiome di una cometa ............................................................................................ 30
Figura 18: Asteroide ................................................................................................................... 35
Figura 19: Meteorite ferrosa...................................................................................................... 36
Figura 20: Meteorite roccisa ...................................................................................................... 36
44