il teorema di norton - Ing. Matilde Consales Home Page

IL TEOREMA DI NORTON
Il teorema di Norton si usa per trovare più agevolmente una grandezza (corrente o tensione) in una
rete elettrica.
Enunciato: una rete elettrica vista a una coppia qualsiasi di morsetti è equivalente ad un circuito
composto da un generatore di corrente IN con in parallelo un resistore RN.
Il valore IN corrisponde alla corrente di cortocircuito cioè alla corrente presente ai terminali
considerati quando sono collegati tra di loro (cortocircuitati). La RN è la resistenza dell'intera rete ai
morsetti considerati che si determina annullando gli effetti di tutti i generatori presenti nella rete:
sostituendo un cortocircuito ad ogni generatore di tensione ed un circuito aperto ad ogni generatore
di corrente.
Esercizio 1
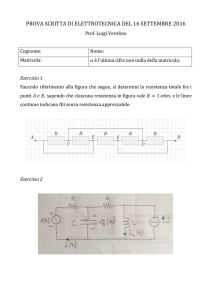
Dato il circuito di figura 1 trovare la corrente che scorre nel resistore R4.
Figura 1
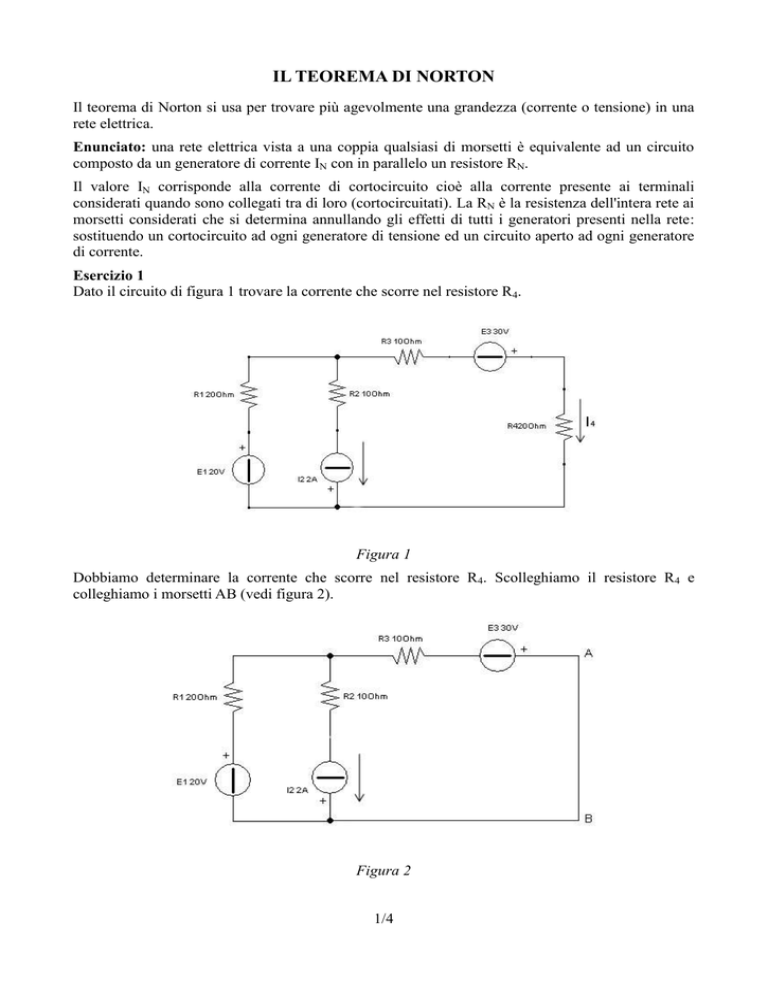
Dobbiamo determinare la corrente che scorre nel resistore R4. Scolleghiamo il resistore R4 e
colleghiamo i morsetti AB (vedi figura 2).
Figura 2
1/4
Determinazione della resistenza equivalente RN:
Per determinare RN dobbiamo sostituire un cortocircuito ad ogni generatore di tensione ed un
circuito aperto ad ogni generatore di corrente. Otteniamo il circuito di figura 3.
Figura 3
Se collegassimo un ohmetro ai norsetti AB misureremmo una resistenza pari alla serie delle
resistenze R1 ed R3, quindi:
𝑅𝑁 = 𝑅2 + 𝑅3 = (20 + 10)Ω = 30Ω
Determinazione del generatore equivalente IN:
La corrente erogata dal generatore equivalente è la corrente di cortocircuito che scorre nel cavo che
collega i morsetti AB. (Vedi figura 4).
Figura 4
Nel ciscuito dato sono presenti 3 generatori. Troviamo la corrente di cortocircuito con la
sovrapposizione degli effetti.
Contributo di E1:
Facendo agire solo il generatore di tensione E1 troviamo lo schema di figura 5:
Figura 5
2/4
Si vede che abbiamo una sola maglia: il resistore R2 è scollegato e gli altri due sono in serie quindi
il circuito si riduce a quello di figura 6.
Figura 6
La corrente di corticircuito è data da:
′
𝐼𝑐𝑐
=
𝐸1
20
20
=
𝐴=
𝐴 = 0,66𝐴
𝑅1 + 𝑅3 20 + 10
30
Notare che il verso è concorde con la corrente di cortocircuito.
Contributo di I2:
Facciamo agire solo il generatore di corrente.
Figura 7
La corrente del generatore si distribuisce nei due rami del circuito secondo i versi indicati in figura
7 (imposti dal generatore). Lo schema rappresenta un partitore di corrente. Notare che il verso della
corrente di cortocircuito è discorde rispetto a quello della corrente sul resistore R3.
′′
𝐼𝑐𝑐
= −𝐼𝑅3 = −𝐼2
𝑅1
20
40
= −2
𝐴 = − 𝐴 = −1,33𝐴
𝑅1 + 𝑅3
20 + 10
30
Contributo di E3:
Troviamo, infine, il contributo del generatore E3.
Figura 8
3/4
Anche in questo caso abbiamo una sola maglia. Il resistore R2 è scollegato e R1 e R3 sono in serie
quindi:
′′′
𝐼𝑐𝑐
=
𝐸3
30
30
=
𝐴=
𝐴 = 1𝐴
𝑅1 + 𝑅3 20 + 10
30
A questo punto possiamo trovare la corrente del circuito equivalente che è data da:
′
′′
′′′
𝐼𝑁 = 𝐼𝑐𝑐
+ 𝐼𝑐𝑐
+ 𝐼𝑐𝑐
= (0,66 − 1,33 + 1)𝐴 = 0,33𝐴
Disegnamo il circuito equivalente:
Figura 9
A questo punto possiamo calcolare la corente richiesta con il partitore di corrente. Facciamo
attenzione ai segni: abbiamo sempre clcolato la corrente di cortocircuito verso il basso quindi il
generatore equivalente di Norton va disegnato come in figura. La corrente che scorre nel resistore
R4 è verso l’alto (rappresenta, infatti, una parte della corrente del generatore che si divide tra i due
rami). Nell’esercizio ci viene richiesto di trovare la corrente I4 verso il basso pertanto le due correnti
sono discordi.
𝐼4 = −𝐼𝑁
𝑅𝑁
30
30
= −0,33
𝐴 = −0,33 𝐴 = 0,2𝐴
𝑅𝑁 + 𝑅4
30 + 20
50
Questo file può essere scaricato gratuitamente. Se pubblicato citare la fonte.
Matilde Consales
4/4