Prova del 16-9-2016

PROVA SCRITTA DI ELETTROTECNICA DEL 16 SETTEMBRE 2016
Prof. Luigi Verolino
Cognome:
Nome:
Matricola:
 è l’ultima cifra non nulla della matricola:
Esercizio 1
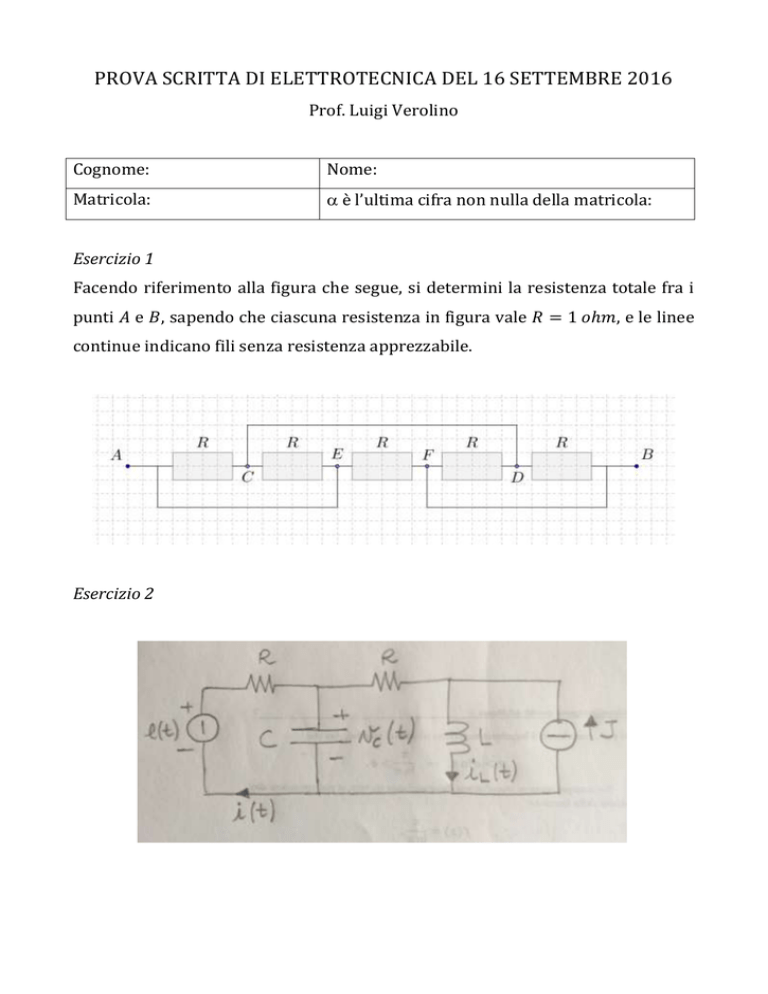
Facendo riferimento alla figura che segue, si determini la resistenza totale fra i
punti 𝐴 e 𝐵, sapendo che ciascuna resistenza in figura vale 𝑅 = 1 𝑜ℎ𝑚, e le linee
continue indicano fili senza resistenza apprezzabile.
Esercizio 2
Per la rete mostrata in figura, alimentata da un generatore in continua 𝐽 = 1 e
dal generatore variabile nel tempo
𝑒(𝑡) = 𝐸 sin(𝜔𝑡) u(𝑡) con 𝐸 = 𝛼, 𝜔 =
1000
,
𝛼
si determini l’andamento della corrente che attraversa l’induttore in ogni istante
di tempo. Si assuma che
𝑅 = 𝛼, 𝐿 = 𝛼 2 𝑚𝐻 , 𝐶 = 1 𝑚𝐹 .
Valutazione della prova scritta
Esercizio 1
Esercizio 2
Complessivo
Valutazione della prova orale
Domanda 1
Domanda 2
Domanda 3
Voto finale
Esercizio 1
La difficoltà del circuito è visiva: esso va ridisegnato, considerando coincidenti
quei punti che sono collegati da un cortocircuito. Così 𝐴 viene collegato da una
parte a 𝐶, attraverso il parallelo di due resistori, dall’altra a 𝐵 attraverso un
resistore. La stessa cosa si può dire per il nodo 𝐵. Si osserva poi che i nodi 𝐴 ed 𝐸
sono equipotenziali, essendo collegati da un cortocircuito, e quindi coincidono;
la stessa cosa si può dire per i nodi 𝐵 e 𝐹. Ciò comporta che i resistori dei rami
𝐴𝐶 e 𝐶𝐸, come pure quelli dei rami 𝐹𝐷 e 𝐷𝐵, sono in parallelo. D’altra parte,
anche i nodi 𝐶 e 𝐷 coincidono. Le precedenti considerazioni consentono di
trasformare la rete come mostrato nella figura che segue, da cui si evince che sui
rami 𝐸𝐶 e 𝐷𝐵 vi sono due resistori uguali di valore 𝑅/2: essi sono in serie, che
poi è in parallelo con il resistore 𝐸𝐹. Per ottenere il valore della resistenza
equivalente 𝑅𝐴𝐵 vista dai morsetti 𝐴 e 𝐵, basta allora scrivere che
𝑅𝐴𝐵 = 𝑅𝐸𝐹 ∥ (𝑅𝐸𝐶 + 𝑅𝐷𝐵 ) = 𝑅 ∥ 𝑅 =
𝑅
= 0.5 𝑜ℎ𝑚 .
2
Esercizio 2
Si osserva preliminarmente che, applicando la sovrapposizione degli effetti in un
qualsiasi istante di tempo, si può scrivere che la corrente che fluisce
nell’induttore è pari alla somma di due termini
𝑖𝐿 (𝑡) = 𝐽 + 𝑎(𝑡) ,
in cui si è indicato con 𝑎(𝑡) la componente alternata della corrente. Operando in
questa maniera, si può eliminare dalla rete il generatore di corrente continua,
ottenendo una netta semplificazione dello studio della dinamica del circuito.
La rete in cui circola la corrente 𝑎(𝑡) è dunque priva del generatore di corrente
ed è a riposo prima che il generatore inizi a funzionare, sicché
𝑣𝐶 (𝑡) = 0 , 𝑎(𝑡) = 0 per 𝑡 < 0 .
Pertanto, le condizioni di raccordo sono
𝑣𝐶 (0) = 0 , 𝑎(0) = 0 .
Per 𝑡 > 0, la rete è descritta dalle tre equazioni
𝑖 =𝑎+𝐶
𝑑𝑣𝐶
𝑑𝑎
, 𝑣𝐶 = 𝑅𝑎 + 𝐿
, 𝑒 = 𝑅𝑖 + 𝑣𝐶 .
𝑑𝑡
𝑑𝑡
Eliminando la corrente 𝑖(𝑡) che attraversa il generatore di tensione, la quiale
d’altronde non è una variabile di stato, si ottengono due sole equazioni
𝑣𝐶 = 𝑅𝑎 + 𝐿
𝑑𝑎
𝑑𝑣𝐶
, 𝑒 = 𝑅𝐶
+ 𝑅𝑎 + 𝑣𝐶 ,
𝑑𝑡
𝑑𝑡
che, nel limite per 𝑡 → 0+ , forniscono i valori delle derivate
𝑑𝑎(0+ )
𝑑𝑣𝐶 (0+ )
=0,
=0.
𝑑𝑡
𝑑𝑡
Eliminando la tensione sul condensatore, non è difficile ottenere l’equazione
differenziale
𝑑2𝑎
1
𝑅 𝑑𝑎 2𝑎 𝐸 sin(𝜔𝑡)
+
+
+
=
,
(
)
𝑑𝑡 2
𝑅𝐶 𝐿 𝑑𝑡 𝐿𝐶
𝑅𝐿𝐶
che deve essere risolta con le due condizioni iniziali
𝑑𝑎(0+ )
𝑎(0) = 0 ,
=0.
𝑑𝑡
L’equazione caratteristica
1
𝑅
2
2000
2 ∙ 106
2
𝜆 + ( + )𝜆 +
=0 → 𝜆 +
𝜆+
=0
𝑅𝐶 𝐿
𝐿𝐶
𝛼
𝛼2
2
ammette due soluzioni complesse e coniugate
𝜆1,2 = −
1000 1000
±
𝑗 = −𝜔 ± 𝜔𝑗 .
𝛼
𝛼
Pertanto, l’integrale dell’omogenea vale
𝑎0 (𝑡) = e−𝜔𝑡 [𝐾1 cos(𝜔𝑡) + 𝐾2 sin(𝜔𝑡)] .
L’integrale particolare, poi, va cercato con il metodo dei fasori, per cui
𝐸 = 𝑍̇ 𝐼 con 𝑍̇ = 𝑅 + (𝑅 + 𝑗𝑋𝐿 ) ∥ (−𝑗𝑋𝐶 ) = 2𝛼 − 𝑗𝛼 ,
in cui si è posto
𝐸 = 𝐸 = 𝛼 , 𝑋𝐿 = 𝜔𝐿 = 𝛼 , 𝑋𝐶 =
1
=𝛼.
𝜔𝐶
Segue che la corrente nell’induttore vale
𝐴𝑝 = 𝐼
−𝑗𝑋𝐶
1 − 2𝑗
=
.
𝑅 + 𝑗𝑋𝐿 − 𝑗𝑋𝐶
5
Discende da quanto scritto che, nel dominio del tempo, risulta
1
2
𝑎𝑝 (𝑡) = sin(𝜔𝑡) − cos(𝜔𝑡)
5
5
e, quindi, l’integrale generale
𝑎(𝑡) = 𝑎0 (𝑡) + 𝑎𝑝 (𝑡)
si può scrivere come
1
2
𝑎(𝑡) = e−𝜔𝑡 [𝐾1 cos(𝜔𝑡) + 𝐾2 sin(𝜔𝑡)] + sin(𝜔𝑡) − cos(𝜔𝑡) .
5
5
Se si impone la prima condizione iniziale, si ottiene immediatamente
𝑎(0) = 0 → 𝐾1 =
2
.
5
Forzando poi la seconda condizione iniziale, risulta
𝑑𝑎(0+ )
𝜔
1
=0 →
− 𝜔𝐾1 + 𝜔𝐾2 = 0 → 𝐾2 = .
𝑑𝑡
5
5
In definitiva, la corrente nell’induttore è descritta dall’equazione
1
2
𝑖𝐿 (𝑡) = 1 + sin(𝜔𝑡) (1 − e−𝜔𝑡 ) − cos(𝜔𝑡) (1 + e−𝜔𝑡 ) per 𝑡 ≥ 0 .
5
5
La figura precedente riporta, in rosso, l’andamento della corrente che fluisce
attraverso l’induttore in funzione della variabile adimensionale 𝜔𝑡, in verde,
quello del solo integrale particolare. Si nota che, dopo un transitorio della durata
di circa 5/𝜔, le due curve coincidono.