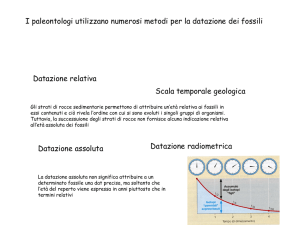
Fondamentali
di genetica
delle popolazioni
Genetica delle popolazioni
Si occupa:
- delle frequenze dei geni e dei genotipi nelle popolazioni
- del loro cambiamento lungo le generazioni
… e quindi di:
- evoluzione
- selezione naturale e artificiale
Genetica delle popolazioni
Popolazione
Gruppo di individui sessuati a fecondazione incrociata che si
dividono un pool genico comune
Una tale popolazione (di piante allogame, ad esempio) è costituita da
individui altamente eterozigoti e tutti geneticamente diversi tra loro
Consideriamo il solito locus A con due alleli, A e a
Una popolazione è costituita così:
AA
250 (D)
x = 250/1000 = 0,25 = D/N
Aa
600 (H)
y = 600/1000 = 0,60 = H/N
aa
150 (R)
z = 150/1000 = 0,15 = R/N
Tot. 1000 (N)
Genotipi
Frequenze genotipiche
1,00
AA
x
Aa
y
Def. Frequenza genotipica:
frequenza di un genotipo in
una popolazione
aa
z
x+y+z=1
Genetica delle popolazioni
Genotipi
Frequenze genotipiche
AA
x
Aa
y
aa
z
Calcoliamo le frequenze degli alleli A e a
Gli alleli A sono: (2D+H)/2N; quelli a sono (2R+H)/2N, ma più semplicemente:
Frequenze geniche
p(A) = x + 1/2y
q(a) = z + 1/2y
Nel nostro esempio:
x = 0,25
y = 0,60
z = 0,15
Def. Frequenza genica:
frequenza di un allele nei loci
disponibili per esso in una
popolazione
p(A) = x + 1/2y = 0,55
q(a) = z + 1/2y = 0,45
p + q = x + 1/2y + z + 1/2y = x + y+ z = 1
Genetica delle popolazioni
Se tutti gli individui hanno uguali possibilità di riprodursi,
le frequenze dei gameti corrispondono alle frequenze geniche.
Quindi la generazione successiva, con incroci casuali (panmissia), sarà
costituita così:
Gameti
+
p(A)
q(a)
p(A)
p2(AA)
pq(Aa)
q(a)
pq(Aa)
q2(aa)
La legge di Hardy-Weinberg stabilisce che in una generazione di unioni a
caso le frequenze genotipiche raggiungono l’equilibrio alle frequenze:
p2(AA) + 2pq(Aa) + q2(aa)
Genetica delle popolazioni
Esercizi
1. Una popolazione è composta da 750 individui AA e 250
individui Aa.
a. Quali sono le frequenze geniche?
b. Quali saranno le frequenze genotipiche e geniche nella
generazione successiva?
2. Una popolazione è composta da 500 individui AA, 250 individui Aa e 50
individui aa.
a. La popolazione è in equilibrio?
b. Quali saranno le frequenze genotipiche alla generazione successiva, con
unioni casuali?
3. In una popolazione in equilibrio gli individui con genotipo aa sono il
16%. Determinare le frequenze geniche e genotipiche
4. Costruisci un foglio excel per il calcolo e la verifica dell'equilibrio HW
date le frequenze assolute dei tre genotipi
Genetica delle popolazioni
Le condizioni dell’equilibrio H-W
* Popolazione numerosa
* Unioni casuali (panmissia)
Le unioni non sono casuali quando avvengono:
* tra individui fenotipicamente o geneticamente simili: inbreeding
* tra individui fenotipicamente o geneticamente dissimili: outbreeding
* Costanza delle frequenze geniche:
Assenza di mutazione differenziale
Assenza di migrazione
Assenza di selezione
Miglioramento genetico = Aumentare le frequenze
degli alleli favorevoli mediante selezione
Genetica delle popolazioni
Selezione
Il breeder sceglie, seleziona, gli individui che hanno le caratteristiche
desiderate con l'obiettivo di trasmetterle alle progenie
Si ha selezione, naturale o artificiale, quando alcuni genotipi hanno
fertilità maggiore di altri e quindi contribuiscono alla generazione
successiva in misura diversa
Fitness (W) o valore di adattamento
o valore selettivo
è il parametro della selezione ed esprime contributo di ciascun genotipo
alla generazione successiva, in termini di numero di figli
Posto uguale a 1 il numero di figli dell’individuo che fa più figli, la fitness
degli altri individui viene definita in relazione a questo valore massimo
0<W<1
Genetica delle popolazioni
Se la fitness di un individuo è legata ai geni che porta,
la frequenza dei geni degli individui con fitness più elevata aumenterà
da una generazione all’altra, mentre le frequenza dei geni
che determinano una bassa capacità riproduttiva diminuirà
La selezione modifica le frequenze geniche
Coefficiente di selezione S = 1-W
Esprime il minor contributo di un genotipo alla generazione successiva
rispetto al genotipo con fitness pari a 1
Esempio: Se la selezione sfavorisce l’omozigote recessivo e in presenza di
dominanza completa al locus A si ha:
AA
Aa
aa
W=1
W=1
W=1-s
AA
Aa
aa
Nel caso estremo di
un recessivo letale:
W=1
W=1
W=0
Genetica delle popolazioni
Esempio: la selezione sfavorisce l'omozigote recessivo
Genotipi
Frequenze
Fitness
AA
Aa aa
p2 + 2pq + q2
1
1
1-s
Frequenze dopo che ha agito la selezione (un ciclo):
p2 + 2pq + q2(1-s) = p2 + 2pq + q2 - sq2 = 1- sq2
Per far sì che la somma delle frequenze sia =1:
Genotipi
AA
Frequenze
Aa
aa
p
2pq
q (1-s)
+
+
1- sq2
1- sq2
1- sq2
2
2
Genetica delle popolazioni
Dopo la selezione, quindi, la frequenza di a (q1) sarà (secondo la
formula q= z + 1/2y):
q1 =
q2(1-s)
1- sq2
+
pq
1- sq2
q - sq2
= …. =
1- sq2
Per convenzione, l'effetto della selezione si misura con la variazione di q:
- sq2(1-q)
q - sq2
–
q
=
…
=
1- sq2
1- sq2
Hq = q1 – q =
La selezione contro il recessivo è tanto più efficace
quanto maggiori sono q e s
Genetica delle popolazioni
Esempio: il destino di un allele letale recessivo che determina albinismo
nelle piante
Poniamo che una popolazione abbia le frequenze genotipiche e geniche seguenti:
1/3AA + 2/3Aa
;
p=2/3; q=1/3
Le frequenze genotipiche e geniche della generazione successiva saranno quelle
volute dall’equilibrio H-W:
p2 (AA) + 2pq (Aa) + q2 (aa)
Si ha quindi:
Cioè:
1/2AA + 1/2Aa
4/9 AA + 4/9 Aa + 1/9 aa
e
Alla generazione successiva analogamente, si avrà:
Infatti:
q - sq2
q1 =
=
1- sq2
q1 =
p=3/4; q=1/4
p=4/5; q=1/5 … e così via
q(1- q)
q(1- q)
=
1- q2
(1+q)(1- q)
q
1+q
Formula di Li
Genetica delle popolazioni
q1 = q/(1 + q)
qt = q/(1 + tq),
da cui:
t = 1/qt + 1/q
Con questa formula possimo calcolare la diminuzione della frequenza di
un allele letale recessivo nel corso di successive generazioni di
interincrocio casuale, e calcolare il numero di generazioni (t) necessario
per ridurre la frequenza di una quantità voluta
Genetica delle popolazioni
Esercizio
Quante generazioni ci vogliono per dimezzare la frequenza di un recessivo letale
a partire dalla frequenza iniziale q = 0,4 ?
t = 1/qt + 1/q = 1/0,2 + 1/0,4 = 5 + 2,5 = 7,5
E quante generazioni ci vogliono per dimezzare ancora la frequenza a 0,1?
t = 1/0,1 + 1/0,2 = 10 +5 = 15
E per dimezzare ancora la frequenza a 0,05?
t = 1/0,05 + 1/0,1 = 20 + 10 = 30
Quando la frequenza è piccola la selezione è poco efficace anche
contro alleli letali
Genetica delle popolazioni
Modello generale della selezione
Genotipi
Frequenze
AA
Aa aa
p2 + 2pq + q2
Fitness
W0
W1
W2
Fitness media
p2W0 + 2pqW1 + q2W2 = W
o valore adattativo medio
Dopo la selezione le frequenze genotipiche saranno:
p2W0
+
W
2pqW1
+
q2W2
W
=1
W
La frequenza genica di a dopo la selezione, sarà:
q1 =
q2W2
W
+
pqW1
=
q(qW2+ pW1)
W
W
Genetica delle popolazioni
Hq = q1 – q =
Hq =
q(qW2+ pW1)
p2W0 + 2pqW1 + q2W2
– q = …....
pq[q(W2- W1) + p(W1- W0)]
W
Il modello generale della selezione ci dice che la selezione è più
efficace con frequenze geniche di 0,5 e quando la fitness media è
bassa
Genetica delle popolazioni
Esercizi
1. Calcolare Hq nel caso di dominanza completa e selezione contro
l'omozigote recessivo (W0=W1=1; W2=1-s)
2. Calcolare Hq nel caso di dominanza completa e selezione contro il
dominante (W0=W1=1-s; W2=1). Cosa avviene quando s=1?
3. Calcolare Hq nel caso di selezione contro entrambi i dominanti
(W0=1-s1; W1=1; W2=1-s2). Calcolare il valore di q all'equilibrio
Genetica delle popolazioni
Inbreeding
E’ un sistema di unioni in cui le unioni tra individui
imparentati è più frequente di quanto voluto dal caso
Può prodursi nel caso di popolazioni costituite da un numero
piccolo di individui o molto stanziali, o per intervento dell’uomo
La conseguenza è l’aumento della percentuale di omozigoti per alleli identici
Alleli identici sono alleli che
hanno la stessa origine.
Sono cioè copie di
un unico allele presente
inizialmente in un individuo e
originatisi per replicazione
del DNA
x
Aa
AA Aa
aa
AA
AA
Aa
alleli diversi
alleli identici
alleli simili
L’omozigosi per alleli identici è molto improbabile in un sistema di unioni casuale, mentre
è tanto più probabile quanto più stretta è la parentela tra gli individui che si uniscono
In zootecnia si utilizza il termine Consanguineità
Qual è la forma di inbreeding più “stretto” ?
Genetica delle popolazioni
La probabilità che un individuo estratto a caso da una popolazione possieda
alleli identici è stata assunta come misura del grado di inbreeding della
popolazione. Tale probabilità è espressa dal
Coefficiente di inbreeding: F
(Sewall-Wright, 1922)
0<F<1
F = 0 individuo non omozigote per alleli identici (per tutti i suoi geni)
F = 1 individuo omozigote per alleli identici (per tutti i suoi geni)
Quindi F esprime allo stesso tempo:
la percentuale di individui omozigoti per alleli identici in una popolazione
la percentuale dei geni omozigoti per alleli identici di ciascun individuo
Genetica delle popolazioni
Calcolo del Coefficiente di inbreeding F
Unione fratello-sorella
Qual è la probabilità che:
A
B
H1H2
H3H4
C
D
E
In generale:
E sia omozigote H1H1:
(1/2)(1/2) (1/2)(1/2)=(1/2)4
E sia omozigote H2H2:
(1/2)(1/2) (1/2)(1/2)=(1/2)4
E sia omozigote H1H1 o H2H2:
2(1/2)4
E sia omozigote H3H3 o H4H4:
2(1/2)4
E sia omozigote H1H1 o H2H2 o H3H3 o H4H4: 4(1/2)4
FX = Σ(1/2)n+1(1 + Fy)
Dove:
Σ fa riferimento a tutti gli antenati comuni ai genitori
dell’individuo considerato
n è il numero di passi generazionali che vanno da un
genitore all’altro dell'individuo considerato attraverso
l’antenato comune
Fy è il coefficiente di inbreeding dell’antenato comune
FE=
4(1/2)4 = 4/16 = 0,25
probabilità che E sia
omozigote
per alleli identici
Genetica delle popolazioni
Nota
Coefficiente di parentela
Probabilità che due individui (A e B) possiedano alleli identici.
PAB = Σ(1/2)n(1 + Fy)
E' il doppio del coefficiente di inbreeding della loro progenie.
E' un parametro molto utilizzato in campo animale per decidere quali
individui vengono fatti accoppiare
Genetica delle popolazioni
Esercizio
Calcola il coefficiente di inbreeding del toro Comet, uno dei capostipiti
della razza Shorthorn, il cui pedigree è qui rappresentato
?
Lady Maynard
Foljambe
Young
Strawberry
Phoenix
Bolingbroke
Favourite
Young Favourite
Comet
Genetica delle popolazioni
Esercizi
1. Calcola l’omozigosi teorica nella F4 di un triibrido, nell’ipotesi che i 3 geni siano
indipendenti.
2. Calcola il coefficiente di inbreeding del cane Crack che ha il pedigree rappresentato in
figura.
TERRI
FUFI
DODI
BILLI
LILLI
BIRBA
JACK
BOBI
PIPPI
CRACK
L’effetto dell’inbreeding sull’equilibrio Hardy-Weinberg
Se una popolazione è inbred essa avrà una percentuale di omozigoti per alleli
identici pari a F e la percentuale totale di omozigoti sarà maggiore di quanto
voluto dalla legge di H-W
Gli F omozigoti per alleli identici, per un gene A, si ripartiranno tra le due
forme alleliche: pF(AA) + qF(aa) = F
La parte restante della popolazione (1-F) avrà le frequenze genotipiche
previste dalla legge di H-W:
p2(1-F)(AA) + 2pq(1-F)(Aa) + q2(1-F)(aa)
Sommando:
f(AA) = p2(1-F) + pF = p2 – p2F + pF = p2 + pF(1-p) = p2 + pqF
f(Aa) = 2pq(1-F)
= 2pq- 2pqF
2
f(aa) = q (1-F) + qF = q2 – q2F + qF = q2 + qF(1-q) = q2 + pqF
E quindi:
(p2 + pqF)(AA) + (2pq- 2pqF)(Aa) + (q2 + pqF)(aa)
Formula dell’equilibrio di Sewall-Wright
Genetica delle popolazioni
L’effetto dell’inbreeding sul fenotipo
Depressione da inbreeding
Diminuzione del vigore e della fertilità (e quindi della produttività) in
conseguenza di unioni inbred
Eterosi (Shull, 1905)
Esplosione di vigore e
fertilità (e quindi di
produttività) quando si
uniscono particolari
genitori (linee) inbred
per ottenere un
“ibrido” F1)
N.B.
L'entità della depressione
da inbreeding e
dell'eterosi varia in
funzione della specie e
del genotipo
F1
Generazioni di autofecondazione
1 2
3
4
5
6
7
Inbred
parentali
D.F. Jones, Genetics 9:405-418, 1922
Genetica delle popolazioni
Eterosi in mais
Plant Cell, Vol. 15,
2236–2239, 2003
Sfruttamento dell'eterosi in mais
Incroci
semplici
Incroci
doppi
Impollinaz. libera
Troyer 1990
Ma può esserci (e quasi sempre c'è) eterosi anche in piante autogame !
Genetica delle popolazioni
Eterosi in piante da orto
Immagini Gianni Barcaccia, 2008
Genetica delle popolazioni
Eterosi
George H. Shull (1911) “the superiority of heterozygous genotypes over the
corresponding homozygotes”
Mid-parent heterosis
P1
High-parent heterosis
P1
F1 P2
P2 F1
Ha rilevanza pratica
–
HF1 = F1 – P
– –
HF1 (%) = 100(F1 – P)/P
HF1 = F1 – PM
HF1 (%) = 100(F1 – PM)/PM
Basi genetiche dell'eterosi
• Dominanza direzionale, e/o
• Superdominanza/pseudosuperdominanza, e/o
• Epistasi
Un modello utile per misurare l'effetto dell'inbreeding su un
carattere quantitativo
Un gene che contribuisce, insieme ad altri, al controllo di un carattere
quantitativo può essere descritto così:
h
Assenza di dominanza:
Dominanza incompleta:
-a
0
a
I
I
I
aa
Aa
AA
-a
0
h
a
I
I
I
I
Aa AA
aa
Dominanza completa:
-a
0
I
I
aa
h
a
I
AA
Aa
Il modello assume pari a 0 il valore della media tra i due omozigoti aa e
AA, e che la sostituzione dell'allele a con A incrementa il valore del
carattere quantitativo di una quantità a
Effetto dell'inbreeding sui caratteri quantitativi
Genotipi
Valore genotipico
Frequenza
Prodotto
AA
a
p2
p2a
Aa
h
2pq
2pqh
aa
-a
q2
q2(-a)
Il valore genotipico medio della popolazione è:
p2a + 2pqh + q2(-a) = (p2 – q2)a + 2pqh = (p – q)a +2pqh
Popolazione inbred:
Genotipi
Valore genotipico
Frequenza
Prodotto
AA
a
p2 +pqF
(p2 +pqF)a
Aa
h
2pq - 2pqF
(2pq-2pqF)h
aa
-a
q2 + pqF
(q2-pqF)(-a)
Il valore genotipico medio della popolazione è:
p2a + pqFa + 2pqh -2pqFh + q2(-a) – pqFa = …. = (p – q)a +2pqh - 2pqFh
2pqFh misura le depressione da inbreeding: è proporzionale ad h e da F
Genetica delle popolazioni
Ipotesi della dominanza (Jones)
HF1 = Σh
-a
0
h
a
I
I
I
I
Come abbiamo visto, la media di una popolazione inbred diminuisce
di 2pqhF rispetto alla popolazione panmittica a causa dell'omozigosi
per alleli (identici) recessivi sfavorevoli
Inbred 1
AA bb CC DD ee FF GG hh II ll
Inbred 2
x
aa BB cc dd EE ff gg HH ii LL
F1
Aa Bb Cc Dd Ee Ff Gg Hh Ii Ll
In questo ibrido tutti i geni sono in condizione eterozigote e
quindi nessuno dei recessivi sfavorevoli si manifesta
Perchè ci sia eterosi la dominanza deve essere “direzionale”: tutti,
o la gran parte, dei loci che controllano il carattere devono avere
dominanza nella stessa direzione, con l'allele dominante che
incrementa il carattere
Dovrebbe allora essere possibile ottenere una inbred vigorosa
quanto il migliore ibrido....
Si, ma a condizione che avvengano tutti gli eventi di
ricombinazione necessari, inclusi i crossing-over tra geni associati!
AA BB CC DD EE FF GG HH II LL
In effetti, nel mais, grazie alla selezione ricorrente che va avanti
da 100 anni, le inbred di oggi sono molto migliori di quelle di una
volta ...
Eterosi
Ipotesi della
superdominanza
-a
0
a
h
I
I
I
I
L'eterozigote supera entrambi gli omozigoti
E' stata dimostrata solo per alcuni geni, ad esempio mutazioni
clorofilliane in orzo (Gustafsson)
Single locus overdominance
in pomodoro: Single flower
truss (Sft). Krieger et al.
Nature Genetics 42, 459–463, 2010
Genetica delle popolazioni
East propose che la diversità allelica sia legata al vigore, e che esistano alleli
via via “divergenti” che combinandosi insieme nell'ibrido danno effetti di
eterosi diversi:
Alleli multipli
a1 > a2 > a3 > a4 …
Combinazioni ibride
a1a4 > a1a3 > a1a2 > a1a1
Gruppi eterotici
popolazioni o gruppi di popolazioni che “combinano bene” tra loro:
Incroci tra piante appartenenti a gruppi eterotici diversi presentano eterosi
elevata
Secondo l'ipotesi di East, i gruppi eterotici devono possedere alleli diversi per i
geni che controllano i caratteri che manifestano eterosi
In effetti esistono molti dati in molte specie diverse che legano l'eterosi
alla diversità genetica:
Più sono geneticamente diversi i genitori, più aumenta l'eterosi delle loro
progenie ibride.
Pseudosuperdominanza
L'effetto del linkage in trans tra un gruppo di geni può fare l'effetto della
superdominanza quando in realtà non c'è superdominanza per i singoli geni
Inbred 1
Inbred 2
A b C D e F G h I l
a B c d E f g H iL
x
A b C D e F G h I l
E' rappresentata una porzione
di un cromosoma di due inbred
“complementari”
a B c d E f g H iL
F1
A b C D e F G h I l
a B c d E f g H i L
Se considerassimo questo tratto cromosomico come un
unico locus, concluderemmo che esiste superdominanza
Una visione moderna dell'eterosi
La diversità allelica per geni regolatori (fattori di trascrizione, micro RNA,
ecc.) determina negli ibridi una miriade di interazioni che possono portare
ad espressione non additiva dei geni ricevuti dai genitori
Livello di trascrizione
Esperimenti microarray o RNAseq
Gene Y
Espressione non additiva
Gene X
Espressione additiva
P1
P2
P1
F1
P2
F1
Non è lo stesso grafico della superdominanza?
Equilibrio per due o più geni e squilibrio di linkage
L'equilibrio HW si raggiunge in una generazione, ma solo per ciascun gene
preso singolarmente
Consideriamo due geni, A e B, con frequenze geniche pA, qa, pB, qb
All'equilibrio gli alleli dei due geni si combinano a caso e quindi le
frequenze dei 4 tipi di gameti saranno:
Gameti
Frequenze
AB
pApB
Ab
pAqb
aB
qapB
ab
q aq b
Con l'aiuto di un quadrato di Punnet possiamo determinare le frequenze
genotipiche all'equilibrio:
f(AABB)= p2Ap2B
f(AABb)= 2p2ApBqb
…..
f(aabb)= q2aq2b
Genetica delle popolazioni
Equilibrio per due o più geni e squilibrio di linkage
Immaginiamo di formare una popolazione mescolando un ugual numero di individui con
genotipi AABB e aabb, lasciati poi alla panmissia
Le frequenze geniche iniziali sono: pA= qa= pB= qb= 0,5
Le frequenze gametiche sono inizialmente 0,5 sia per AB che per ab (diverse da quelle
all'equilibrio, pari a 0,25 per tutti i tipi gametici), quindi dopo la prima generazione di
unioni a caso si avrà:
Gameti
0,5(AB)
0,5(ab)
0,5(AB)
0,25(AABB)
0,25(AaBb)
0,5(ab)
0,25(AaBb)
0,25(aabb)
Alla prima generazione si formano solo 4 dei possibili 9 genotipi.
Alla generazione successiva le frequenze gametiche cambieranno per effetto della
segregazione degli eterozigoti. Se A e B sono indipendenti:
f(AB) = 0,25 + 2(0,25)2 = 0,25 + 0,125 = 0,375
f(Ab) = 2(0,25)2 = 0,125
f(aB) = 2(0,25)2 = 0,125
f(ab) = 0,25 + 2(0,25)2 = 0,25 + 0,125 = 0,375
Genetica delle popolazioni
Equilibrio per due o più geni e squilibrio di linkage
Le frequenze gametiche si avvicinano progressivamente a quelle di equilibrio nel corso
delle generazioni di interincrocio casuale.
Abbiamo ipotizzato che A e B siano indipendenti.
Se due geni sono associati, allora la formazione di gameti ricombinanti è possibile solo
grazie al crossing-over e il raggiungimento dell'equilibrio ed è quindi molto più lento
Squilibrio gametico (gametic phase disequilibrium)
In assenza di linkage viene perduto (dissipato) nel corso di pochissime generazioni.
Si parla comunque (non del tutto propriamente) di
Squilibrio di linkage (Linkage disequilibrium, LD)
Il LD si stima, di solito, con il parametro
D = p(AB) - pApB
Dove p(AB) è la frequenza osservata del gamete AB e pa e pB sono le frequenze
geniche di A e B.
Il valore assoluto di D è lo stesso per tutti i gameti ma è di segno positivo per i
gameti parentali e negativo per i ricombinanti.
Genetica delle popolazioni
Equilibrio per due o più geni e squilibrio di linkage
Dt = D0(1-c)t
Questa formula ci permette di calcolare la diminuzione di D dopo t generazioni di
incrocio casuale; c = frequenza di ricombinazione
Lorenzetti et al. 2010
Genetica delle popolazioni
LD e mappe genetiche
La presenza di LD è essenziale per la costruzione di mappe genetiche.
Per fare una mappa si incrociano due genotipi contrastanti e si utilizza la F2 o una
popolazione da reincrocio, quindi c'e stata una sola meiosi che che ha potuto creare
ricombinazione: il LD è massimo
In laternativa si può ricorrere al cosiddetto
LD mapping, o (impropriamente) Association mapping
Nella forma più avanzata si parla di Genome Wide Association Studies (GWAS)
LD mapping è molto utile negli organismi in cui non è possibile creare
popolazioni ad hoc, o anche quando tale creazione sia lunga e
complessa, ma viene oggi utilizzato anche nelle piante
Si utilizzano popolazioni preesistenti cercando associazione tra il carattere studiato
(ad esempio un malattia genetica nell'uomo, o un carattere quantitativo in una pianta
coltivata) con le frequenze alleliche di marcatori molecolari (prevalentemente SNP)
L'ipotesi di base è che il tratto cromosomico dove è ubicato il gene responsabile del
fenotipo di interesse presenti LD almeno con i marcatori più vicini
Genetica delle popolazioni
Questo perchè nel momento in cui è comparso, in un individuo della popolazione,
l'allele responsabile del fenotipo (ad esempio, l'allele mutato M), esso si trovava
accanto a specifici alleli dei marcatori vicini, e assieme ad essi rappresenta una
combinazione di alleli (aplotipo) unica a loci associati .
Questa combinazione di alleli viene progressivamente distrutta dalla
ricombinazione, ma ciò avviene molto lentamente per loci molto vicini tra loro
SNP1
SNP2
SNP3
SNP4
C
A
C
T
A
C
A
M
A
Se disponiamo di molti marcatori molto vicini
possiamo individuare un aplotipo specifico
per il carattere studiato.
Nella genetica umana, con il LD mapping, si cerca di mettere in relazione
particolari aplotipi con la suscettibilità o predisposizione a particolari patologie
L’uso pratico del LD mapping nel miglioramento genetico delle piante oggi è
ancora limitato, anche se ci sono ormai molti studi pubblicati
Genetica delle popolazioni
Zhu et. al. Plant Genome, 2008, 1:5-20
Status and Prospects of Association Mapping in Plants
Genetica delle popolazioni
Genetica delle popolazioni
Selezione genomica (Genomic selection, GS)
Una volta che è stata stabilita l'associazione genome-wide tra
marcatori e caratteri, diventa possibile fare GS
E' una forma di MAS in cui si utilizzano marcatori che coprono l'intero
genoma, scelti in modo tale che tutti i QTL individuati nell'analisi “Genome
Wide” sono in LD con almeno un marcatore.
Si selezionano gli individui della popolazione segregante sulla base degli
alleli favorevoli a tutti i marcatori scelti
E' diventata possibile grazie alla disponibilità di molti SNP e dell'automazione
della loro genotipizzazione
Termolino
Tripòdi
Portis
Formisano
Riccardo
Metologie integrate per la selezione genomica di piante ortive (25)
Metodi di selezione genomica di peperone (20)
Metodi di selezione genomica in melanzana (20)
Metodi di selezione genomica in zucchino (20)
Metodi di selezione genomica in patata (20)
Hamblin et al 2011. Population genetics of genomics-based crop improvement methods. Trends in Genetics 27 (3)
Sommario
Le popolazioni vengono descritte in termini di frequenze geniche e
genotipiche
Le frequenze geniche e genotipiche vengono modificate dalla selezione
Il miglioramento genetico spesso comporta l'incrocio tra individui imparentati
(inbreeding)
I caratteri quantitativi sono soggetti alla depressione da inbreeding in misura
diversa per diverse specie agrarie. L'eterosi è il lato positivo della medaglia!
L'eterosi varia per I diversi caratteri, specie e genotipi, e viene sfruttata
grazie all'incrocio controllato (prossima lezione)
Lo squilibrio di linkage permette di mappare i geni utili ai fini della selezione
e dell'isolamento dei geni
La selezione genomica è resa possibile dalla sintesi delle conoscenze di
genetica delle popolazioni e genetica quantitativa, insieme alle tecniche più
recenti di analisi del genoma (SNP genotyping)
Genetica delle popolazioni