Variabile casuale

Università degli Studi del Piemonte Orientale
Corso di Laurea in Infermieristica
Corso integrato in Scienze della Prevenzione e dei Servizi sanitari
Statistica
Lezione 4
a.a 2011-2012
Dott.ssa Daniela Ferrante
[email protected]
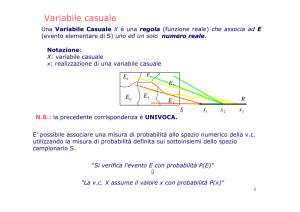
Variabile casuale
La variabile casuale può essere pensata come il risultato
numerico di un esperimento quando non è prevedibile con
certezza.
Ad esempio il risultato del lancio di un dado a sei facce può
essere modellizzato come una variabile casuale che può
assumere i valori 1,2,3,4,5,6
2
Variabile casuale binomiale
Le variabili casuali discrete sono variabili casuali che possono
assumere un numero finito o un’infinità numerabile di valori.
Consideriamo un esperimento i cui risultati possibili sono due:
successo (x=1) e non successo (x=0) e indichiamo con p la
probabilità di successo e con (1-p) la probabilità di non successo.
Se ripetiamo tale esperimento n volte la somma delle
realizzazioni dell’esperimento mi indicherà il numero totale di
successi (k)
3
Variabile casuale binomiale
La variabile casuale binomiale è definita dalla
seguente funzione di probabilità:
Jakob Bernoulli
n=numero di prove
k=numero di successi
p=probabilità di successo
coefficiente binomiale
4
La variabile casuale normale
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
Carl Friedrich Gauss
5
6
7
8
9
10
11
12
13
14
15
X
µ
E’ simmetrica intorno alla media µ
L’area sottesa alla curva è pari ad 1
5
La variabile casuale normale
Uno dei più importanti esempi di variabile casuale
continua è la variabile casuale normale o gaussiana
µ = valore atteso o media
σ = deviazione standard
6
Il grafico seguente mostra due curve normali con DS=1 e
DS=2. Entrambe hanno media=0.
y
0. 40
0. 38
0. 36
0. 34
0. 32
con DS=1
0. 30
0. 28
0. 26
0. 24
0. 22
0. 20
0. 18
con DS=2
0. 16
0. 14
0. 12
0. 10
0. 08
0. 06
0. 04
0. 02
0. 00
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
x0
7
Le variabile casuale normale
µ−3σ
µ − 3σ
µ
− 2σ
µ−2σ
µµ−σ
−σ
µ
µ
µ+σ
µ+σ
µµ+2σ
+2σ
µµ+3σ
+ 3σ
68.27%
95.45%
99.73%
8
Le variabile casuale normale standardizzata
La distribuzione normale standardizzata ha media
pari a 0 e deviazione standard pari ad 1.
0,50
0,50
9
Le variabile casuale normale standardizzata
Qualsiasi valore di un’osservazione x di una distribuzione
normale può essere standardizzato.
Per trasformare x in z (valore standardizzato) si applica la
seguente formula:
z =
x − µ
σ
dove:
x: valore cui siamo interessati
σ: deviazione standard nella popolazione
µ: media nella popolazione
z: deviata normale standardizzata corrispondente ai valori dati per (x, σ, µ)
10
Esempio
• Quale sarà la probabilità di osservare un soggetto con una
statura inferiore a m 1,5928 data una popolazione con altezza
media (µ) 1,730 e deviazione standard (σ) 0,07 (distribuzione
di partenza assunta come normale)?
1,5928 − 1,730
P( X < 1,5928) = P ( Z <
) = P ( z < −1,96) = 0,025
0,07
11
??
z = -1,960
12
Distribuzione normale standard
P
1 coda
0,001 0,01 0,025
3,09 2,33
P
0,001
3,30
1,96
0,05
0,1
1,65
1,29
2 code
0,01
0,025
0,05
0,1
2,58
1,96
1,65
2,33
13
0.025
z = -1,960
14
Esercizio
• Si consideri una popolazione con altezza distribuita come
una Gaussiana con media (µ) = 172,5 cm e deviazione
standard (σ) =6,25 cm.
• Qual è la probabilità di incontrare un individuo estratto da
tale popolazione e di altezza superiore a cm 190?
190 − 172,5
P ( x > 190) = P( z >
) = P ( z > 2,8)
6,25
0,5
0,4
0,001<p<0,01
0,3
0,2
0,1
0
X
-4
-3
-2
-1
0
1
2
3
4
5
6
15
Esercizio
Supponiamo di conoscere che la statura di una certa
popolazione di individui sia approssimativamente
distribuita come una normale con media di 70 pollici e una
deviazione standard di 3 pollici. Qual è la probabilità che
una persona estratta a caso da questo gruppo sia alta tra 65
e 74 pollici?
P(65 < x < 74) = P(−1,67 < z < 1,33) = 1− P(z > 1,33) − P( z < −1,67) =
= 1− 0,10 − 0,05 = 0,85
0,5
0,4
Risultati approssimati
0,3
0,2
0,1
0
X
-4
-3
-2
-1
0
1
2
3
4
5
6
16
La distribuzione t
William Sealey Gosset
La forma della distribuzione t di Student è a
campana con una dispersione maggiore
rispetto alla gaussiana standardizzata
17
La distribuzione t:
– Ha media 0
– E’ simmetrica intorno alla media
– Rispetto alla distribuzione normale è meno appuntita
al centro e ha code più alte
– Tende alla distribuzione normale quando n è
sufficientemente grande
– E’ caratterizzata dai gradi di libertà dove il termine
indica il numero di osservazioni che sono libere di
variare. Si perde un grado di libertà ogni volta che si
stima sul campione un parametro della popolazione.
Per ogni valore dei gradi di libertà c’è una diversa
distribuzione di t. All’aumentare dei gradi di libertà la
distribuzione della t si avvicina alla distribuzione
normale
18
Distribuzione normale (curva blu) e t di student per 1, 2, 3, 5, 10, 30
gradi di libertà
Grafici tratti da: http://en.wikipedia.org/wiki/Student's_t-distribution
19
Distribuzione T
2 code
1 coda
0,005 0,010 0,025 0,050
0,010 0,020 0,050 0,100
Probabilità
gradi libertà
1 63,66 31,82 12,71 6,31
63,66 31,82 12,71 6,31
2 9,22 6,96 4,30 2,92
9,22 6,96 4,30 2,92
3 5,84 4,54 3,18 2,35
5,84 4,54 3,18 2,35
4 4,60 3,75 2,78 2,13
4,60 3,75 2,78 2,13
5 4,03 3,37 2,57 2,02
4,03 3,37 2,57 2,02
6 3,71 3,14 2,45 1,94
3,71 3,14 2,45 1,94
7 3,50 3,00 2,37 1,90
3,50 3,00 2,37 1,90
8 3,36 2,90 2,31 1,86
3,36 2,90 2,31 1,86
9 3,25 2,82 2,26 1,83
3,25 2,82 2,26 1,83
10 3,17 2,76 2,23 1,81
3,17 2,76 2,23 1,81
11 3,11 2,72 2,20 1,80
3,11 2,72 2,20 1,80
12 3,06 2,68 2,18 1,78
3,06 2,68 2,18 1,78
13 3,02 2,65 2,16 1,77
3,02 2,65 2,16 1,77
14 2,98 2,63 2,15 1,76
2,98 2,63 2,15 1,76
15 2,95 2,60 2,13 1,75
2,95 2,60 2,13 1,75
16 2,92 2,58 2,12 1,74
2,92 2,58 2,12 1,74
17 2,90 2,57 2,11 1,73
2,90 2,57 2,11 1,73
18 2,88 2,55 2,10 1,73
2,88 2,55 2,10 1,73
19 2,86 2,54 2,09 1,73
2,86 2,54 2,09 1,73
20 2,85 2,53 2,09 1,73
2,85 2,53 2,09 1,73
per numeri di g.l. superiori a 20 usate la riga corrispondente a 20
20