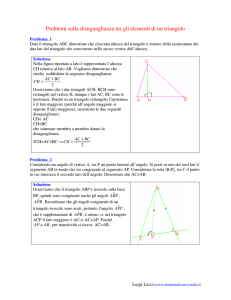
Disuguaglianza triangolare
In ogni triangolo un lato é sempre minore della somma degli altri due
Costruzione di Euclide per la dimostrazione della disuguaglianza triangolare
Euclide dimostrò la disuguaglianza triangolare usando la costruzione in figura. Iniziando con un
triangolo
, si costruisce un triangolo isoscele prendendo il lato
della stessa lunghezza lungo il lato
. Poiché l'angolo
è maggiore dell'angolo
corrispondenti lati opposti vale la stessa disuguaglianza: quindi
, si ha che
e un segme
segmento
, per i
. Ma poiché
, ovvero la disuguaglianza
cercata. Questa dimostrazione compare negli Elementi di Euclide, libro 1, proposizione 20.
Nel caso di triangolo rettangoli, la disuguaglianza afferma che la somma dei due cateti è maggiore
dell'ipotenusa, mentre la differenza è minore di essa.