.
A
p.
1. Funzioni reali di una variabile reale
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
S.
○
Di cosa parleremo
se
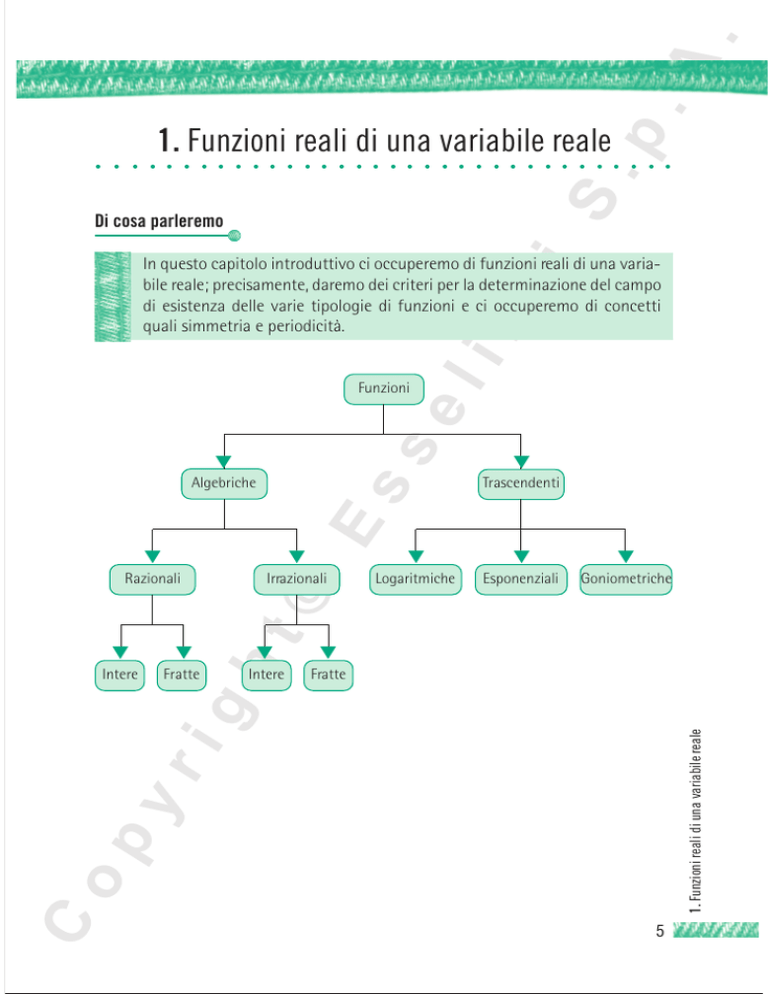
Funzioni
Es
▼
Algebriche
▼
Irrazionali
ht
▼
Fratte
▼
▼
Intere
Fratte
▼
Trascendenti
▼
▼
▼
Logaritmiche
Esponenziali
Goniometriche
C
op
yr
1. Funzioni reali di una variabile reale
ig
▼
©
▼
Razionali
Intere
li
br
i
In questo capitolo introduttivo ci occuperemo di funzioni reali di una variabile reale; precisamente, daremo dei criteri per la determinazione del campo
di esistenza delle varie tipologie di funzioni e ci occuperemo di concetti
quali simmetria e periodicità.
5
.
A
p.
1) Classificazione delle funzioni
li
br
i
S.
Siano X e Y due sottoinsiemi dell’insieme R dei numeri reali, per funzione reale di una variabile reale si intende una legge in base alla
quale a ogni elemento x ∈ X si associano uno o più elementi y di Y.
Se a ogni valore della variabile x (detta variabile indipendente) si fa
corrispondere un solo valore della variabile y (detta variabile dipendente), la funzione si dice univoca (o monodroma); in caso contrario, cioè, se ad almeno un valore della x si fanno corrispondere più
valori della y, la funzione si dice polivoca (o polidroma). Nel seguito, si farà sempre riferimento alle funzioni univoche.
se
A indicare la legge di corrispondenza da X verso Y descritta da una
funzione, si adopera la notazione:
y = f(x)
Es
dove x e y sono, rispettivamente, le variabili indipendente e dipendente, e f rappresenta la legge di corrispondenza descritta dalla funzione.
L’insieme X è detto dominio di definizione (o campo di esistenza)
della funzione; l’insieme Y prende il nome di codominio.
©
Nell’ambito delle funzioni univoche, si è soliti dare la seguente classificazione:
ig
Una funzione si dice algebrica se in essa figurano soltanto operazioni
algebriche, cioè, addizione, sottrazione, moltiplicazione, divisione,
potenza e radice di monomi e polinomi. Le funzioni non algebriche
prendono il nome di trascendenti; a tale insieme appartengono le
funzioni logaritmiche, esponenziali e goniometriche.
yr
Le funzioni algebriche possono essere:
— razionali (intere o fratte);
— irrazionali (intere o fratte).
C
op
1. Funzioni reali di una variabile reale
ht
— funzioni algebriche;
— funzioni trascendenti.
Si dicono razionali quelle funzioni algebriche nelle quali non figurano radici di monomi o polinomi; se, viceversa, in una funzione alge-
6
.
A
p.
S.
brica figura almeno un’operazione di estrazione di radice di un monomio o polinomio, la funzione si dice irrazionale.
L’aggettivo fratta o intera sta a indicare la presenza, o meno, di monomi o polinomi al denominatore di una frazione.
È algebrica razionale intera (o polinomiale) la funzione:
1− x 3
;
4+x2
è algebrica irrazionale intera la funzione:
se
y=
li
y = 2x 3 − 4 x 2 + 3x + 4 ;
mentre è algebrica razionale fratta la funzione:
br
i
Esempi
y=
x +2
x2 +2
;
ht
1
y = ln 2 sen2 x −
2
©
infine, è trascendente la funzione:
Es
y = 3 4 x 4 − 3x 2 − 2 + 4 x 2
mentre è algebrica irrazionale fratta la funzione:
2) Simmetrie e periodicità
ig
Una funzione reale di una variabile reale y = f ( x ) è:
1. Funzioni reali di una variabile reale
yr
— dispari se è simmetrica rispetto all’origine, cioè se:
f ( −x ) = − f (x )
C
op
— pari se è simmetrica rispetto all’asse y, cioè se:
f ( −x ) = f (x )
7
.
A
p.
f ( x + T ) = f ( x ) per ogni x
S.
Una funzione reale di una variabile reale è periodica se esiste T > 0
tale che:
br
i
Le funzioni trascendenti sono periodiche.
Il periodo delle funzioni seno, coseno, secante e cosecante è l’intera
circonferenza, ossia 2π radianti; il periodo della tangente e della cotangente è metà circonferenza, ossia π radianti.
li
3) Campo di esistenza
se
Sia data una funzione reale di una variabile reale y = f(x), il campo di
esistenza, o dominio, della funzione è l’intervallo dei valori di x per
i quali la funzione assume significato.
Es
Per determinare il campo di esistenza di una funzione è utile tener
conto delle seguenti regole o indicazioni:
ht
©
a) nelle funzioni fratte tutti i denominatori delle frazioni devono essere diversi da 0;
b) nelle funzioni irrazionali i radicandi delle radici con indice pari
devono essere ≥ 0;
c) nelle funzioni trascendenti logaritmiche gli argomenti dei logaritmi devono essere > 0;
d) nelle funzioni trascendenti goniometriche si distingue:
ig
π
, con k ∈N ;
2
— gli argomenti della funzione cotangente devono essere diversi
da 2k π con k ∈N .
Nell’ambito della determinazione del campo di esistenza di una stessa
funzione, è possibile che alcune delle condizioni sopra descritte vadano imposte contemporaneamente; ciò, tradotto in termini algebrici,
yr
(2k + 1)
C
op
1. Funzioni reali di una variabile reale
— gli argomenti delle funzioni circolari inverse arcoseno e arcocoseno devono appartenere all’intervallo [-1, 1];
— gli argomenti della funzione tangente devono essere diversi da
8
.
A
p.
S.
equivale a risolvere un sistema di disequazioni, ciascuna delle quali
corrisponde a una delle condizioni imposte.
4) Funzioni limitate
br
i
Una funzione y = f(x) definita in un dato intervallo [a, b] si dice ivi
limitata, se, per ogni valore di x appartenente al suddetto intervallo,
esiste un numero P positivo tale che:
f (x ) ≤ P
li
La funzione è:
Es
se
— limitata superiormente se, nell’intervallo [a, b] esiste un punto
in cui la funzione assume valore M che è non minore dei valori
assunti negli altri punti;
— limitata inferiormente se, nell’intervallo [a, b] esiste un punto in
cui la funzione assume valore m che è non maggiore dei valori
assunti negli altri punti.
5) Funzioni crescenti e decrescenti
yr
Si dicono monotòne le funzioni crescenti, decrescenti, non decrescenti o
non crescenti, ossia le funzioni che variano sempre in uno stesso verso.
6) Funzioni composte
C
op
Sia data la funzione:
y = f (z)
9
1. Funzioni reali di una variabile reale
ht
crescente se x1 < x2 ⇒ f(x1) ≤ f(x2);
costante se x1 < x2 ⇒ f(x1) = f(x2);
decrescente se x1 < x2 ⇒ f(x1) ≥ f(x2);
strettamente crescente se x1 < x2 ⇒ f(x1) < f(x2 );
strettamente decrescente se x1 < x2 ⇒ f(x1) > f(x2).
ig
—
—
—
—
—
©
Sia data una funzione y = f(x), considerati due punti qualsiasi x1 e x2 di
un dato intervallo [a, b], essa si dice:
.
A
p.
S.
dove z non è variabile indipendente, ma a sua volta funzione z = g(x)
della variabile indipendente x, si ha che la funzione:
y = f ( g ( x ))
si dice funzione composta di f e di g.
br
i
Esercizio n. 1
Determinare l’espressione analitica della funzione composta f ( g ( x )) delle due funzioni:
f ( x ) = x 2 e g ( x ) = sen x
li
Entrambe le funzioni hanno dominio e codominio coincidente con l’insieme dei numeri reali.
La funzione composta è la funzione:
f ( g ( x )) = ( sen x ) = sen2 x
2
se
✌
Es
Esercizio n. 2
Determinare le espressioni analitiche delle funzioni composte f ( g ( x )) e g (f ( x )) delle due funzioni:
f ( x ) = x 2 + 1e g ( x ) = e − x
©
Le due funzioni hanno entrambe dominio coincidente con l’insieme dei numeri reali.
La funzione composta di f su g è:
ht
f ( g ( x )) = (e − x ) + 1= e −2 x + 1
2
La funzione composta di g su f è:
+1)
= e −x
2
−1
ig
2
yr
7) Funzioni invertibili
Sia data una funzione:
y = f(x)
essa si dice invertibile in un intervallo chiuso [a, b] se a ogni valore
della x in [a, b] corrisponde uno e un solo valore di y in [a', b'], dove a'
e b' sono il minimo e il massimo della funzione nell’intervallo [a, b], e
op
1. Funzioni reali di una variabile reale
C
(
g (f ( x )) = e − x
✌
10
.
A
p.
S.
viceversa a ogni valore di y in [a', b'] corrisponde uno e un solo valore
di x in [a, b].
La funzione è, pertanto, invertibile nell’intervallo [a, b], se è continua
in [a, b] ed è sempre crescente o sempre decrescente in detto intervallo. La funzione inversa si indica in questo modo:
br
i
x = f –1(y)
li
Negli esercizi che seguono si chiederà di determinare il campo di
esistenza della funzione data e/o le coordinate degli eventuali punti
di intersezione con gli assi.
Queste ultime si determinano risolvendo i due sistemi:
se
x = 0
y = 0
e
y = f ( x )
y = f ( x )
Funzioni iperboliche
Es
Un cenno a parte meritano le funzioni iperboliche che, più volte, saranno trattate nel volume.
©
Le funzioni iperboliche sono così definite:
e x – e –x
e x + e –x
e x – e –x
; coshx =
; tanhx = x – x
2
2
e +e
ht
senhx =
ig
ricavarsi esplicitando rispetto a y l’equazione: x =
e y – e –y
; ricavando ey dalla prece2
yr
dente espressione si ha:
2x = e y –
1 e 2y –1
= y → 2xe y = e 2y –1→ e 2y – 2xe y –1= 0
ey
e
op
ponendo ey = z si ottiene l’equazione di secondo grado:
C
z 2 – 2xz –1= 0 → z12, = x ± x 2 + 1
11
1. Funzioni reali di una variabile reale
La funzione senh è strettamente crescente e quindi invertibile. La funzione inversa è
chiamata settsenh (settore-seno iperbolico), ovvero senh–1 o anche arcsenh. Essa può
.
A
p.
scartando la radice negativa (z è non negativo):
(
)
S.
e y = x + x 2 + 1 → y = senh–1 x = ln x + x 2 + 1
(
br
i
L’insieme di definizione della precedente funzione è tutto l’insieme dei numeri reali R.
Allo stesso modo si ricava l’inversa della funzione cosh. Essendo questa strettamente
decrescente per valori negativi della variabile, strettamente crescente per valori positivi, non è invertibile. È però invertibile la sua restrizione ai valori positivi della variabile.
Ripetendo il procedimento precedente si ricava:
)
La funzione cosh –1 o arcosh è definita per x ≥ 1.
li
cosh–1 x = ln x + x 2 –1
se
La funzione tanh è strettamente crescente in tutto R, quindi invertibile. Sempre con
procedimento analogo a quello usato per ricavare l’inversa del senh, si ottiene:
Es
1 1+ x
tanh–1 x = ln
2 1− x
La funzione è definita per –1 < x < 1.
Esercizio n. 1
©
Determinare il campo di esistenza della funzione:
ht
f ( x ) = x − 2 − x 2 − 2x − 3
Si tratta di una funzione irrazionale in cui per il polinomio sotto radice deve essere:
C
ig
x ≤ −1 e x ≥ 3
✌
yr
per cui, il campo di esistenza è:
op
1. Funzioni reali di una variabile reale
x 2 − 2x − 3 ≥ 0
Risolvendo si ha che la disuguaglianza è verificata per:
12
C .E . = −∞,−1 ∪ 3,+∞
.
A
p.
Esercizio n. 2
f (x ) =
S.
Sia data la funzione:
x
x2 −1
La funzione è irrazionale fratta.
Per quanto concerne il campo di esistenza, deve aversi:
li
1.
br
— il campo di esistenza;
— le coordinate degli eventuali punti di intersezione con gli assi.
i
determinarne:
x 2 − 1> 0 ⇒ x < −1 ∪ x > 1
se
quindi:
✌
C. E. = ]– ∞, –1] ∪ [1, + ∞[
Per le intersezioni con gli assi si ha che l’origine è esclusa dal campo di esistenza, quindi la
curva non interseca l’asse y; inoltre, il numeratore della funzione si annulla solo per x = 0,
punto escluso dal campo di esistenza.
✌
Ne consegue che non vi sono intersezioni con gli assi cartesiani.
Esercizio n. 3
determinarne:
ht
Sia data la funzione:
©
Es
2.
f ( x ) = 32 x -1 − 3x
1. Funzioni reali di una variabile reale
ig
— il campo di esistenza;
— le coordinate degli eventuali punti di intersezione con gli assi.
Per quanto concerne il campo di esistenza, deve aversi:
32 x − 1 − 3 x ≥ 0 ⇒ 32 x − 1 ≥ 3 x ⇒ 2 x − 1 ≥ x ⇒ x ≥ 1
quindi:
C. E. = [1, + ∞[
op
1.
yr
Si tratta di una funzione trascendente.
C
✌
13
.
p.
A
✌
Per le intersezioni con gli assi si ha che l’origine è esclusa dal campo di esistenza, quindi la
curva non interseca l’asse y; per y = 0, si ha:
S.
2.
32 x − 1 − 3 x = 0 ⇒ x = 1
ne consegue che la curva interseca l’asse x nel punto di coordinate (1; 0).
i
Esercizio n. 4
1
ex −2
li
f (x ) =
br
Sia data la funzione:
determinarne:
se
— il campo di esistenza;
— le coordinate degli eventuali punti di intersezione con gli assi.
Si tratta di una funzione trascendente.
Per quanto concerne il campo di esistenza, essendo f ( x ) funzione fratta affinché non si
annulli il denominatore deve essere:
Es
1.
e x − 2 ≠ 0 ⇒ e x ≠ 2 ⇒ x ≠ ln2
In definitiva, si ha:
C .E . = R − {ln2}
✌
Per le intersezioni con gli assi si distingue:
ht
— Per x = 0 si ha:
©
2.
C
1
= −1
1− 2
ig
La funzione interseca l’asse delle y nel punto di coordinate (0,-1).
yr
— Per y = 0 si ha:
1
ex −2
impossibile.
✌
Non c’è intersezione con l’asse delle x.
op
1. Funzioni reali di una variabile reale
✌
y=
14
=0
.
A
p.
1. Stabilire qual è il campo di esistenza della funzione:
S.
Test di verifica
e x −1
e x +1
x
considerando che la funzione e ≠ −1 per ogni x ∈R .
br
li
a) ]−∞, −1] ∪ [1, +∞[
b) R
c) ]−∞, −1]
d) [1,+∞[
se
❏
❏
❏
❏
i
f (x ) =
2. Stabilire qual è il campo di esistenza della funzione:
8
x
©
a) ]−∞, 0 ] ∪ [2, +∞[
b) ]−∞, −2 ] ∪ [2, +∞[
c) R
d) ]−∞, −2 ]
ht
❏
❏
❏
❏
Es
f (x ) = x 2 −
3. Stabilire qual è il punto di intersezione della funzione di cui al quesito
precedente con uno degli assi.
(0;2)
(0; 0)
(2; 0)
❏ b)
1. Funzioni reali di una variabile reale
ig
❏ a)
C
op
yr
❏ c)
❏ d) la funzione non presenta intersezioni con gli assi.
15