Filtro passa-basso
Nei circuiti finora considerati, la rete di retroazione è realizzata solo con
resistenze. E’ tuttavia possibile utilizzare altri elementi passivi (o anche
dispositivi attivi). In figura è mostrato il caso più generale in cui la
retroazione è costituita dalle impedenze Z1(j) e Z2(j) che possono essere
generalmente funzioni della frequenza. Si noti che la retroazione resistiva
è quindi un caso particolare di questa situazione.
Il guadagno (funzione di trasferimento) di questo amplificatore è
determinato utilizzando il procedimento già visto, e pertanto si ha:
AV(j) = - Z2(j) / Z1(j)
Z2 (s)
Z 1(s)
v
+
vs
o
Generalized inverting amplifier configuration
Un esempio di circuito basato su una retroazione che è funzione della
frequenza è il filtro passa-basso a singolo polo, per il quale risulta:
Z1(j) = R1
e
Z2(j) = (R2/jC)/ (R2 + 1/jC) = R2/(1+jC R2)
1
sC
Z 2(s)
R2
R1
v
vs
+
o
Inverting amplifier with frequency dependent feedback
Sostituendo queste relazioni nell’espressione dell’amplificazione si
ottiene:
AV(j) = (- R2/ R1 ) /(1+jC R2) = (- R2/ R1 )* 1/(1+j jC R2)
dove H = 2 fH = 1/ CR2
La figura mostra gli andamenti asintotici relativi al diagramma di Bode del
modulo del guadagno di tensione. La funzione di trasferimento mostra una
caratteristica di tipo passa-basso, con un singolo polo alla frequenza H
che rappresenta la frequenza di taglio superiore (a 3 dB) del filtro passabasso.
A frequenze inferiori, l’amplificatore si comporta come un amplificatore
invertente il cui guadagno è definito dal rapporto delle resistenze R2/ R1 ;
per frequenze maggiori di H , la risposta diventa funzione della frequenza
e mostra un andamento decrescente con pendenza pari a –20 dB per
decade.
A
dB
20 log
R2
R1
-20 dB/dec
log f
fH
Frequency
Bode plot of voltage gain of low-pass filter
Si osservi che il guadagno in banda e la frequenza di taglio possono essere
definiti in maniera indipendente. Poiché vi sono infatti 3 elementi da
dimensionare, la resistenza di ingresso (pari a R1 ) può essere considerata
come un terzo parametro in base al quale stabilire il valore degli elementi
del circuito.
Esercizio: Si progetti un filtro passa.basso con fH = 2 KHz, RIN = 5 Ke
AV = 40 dB.
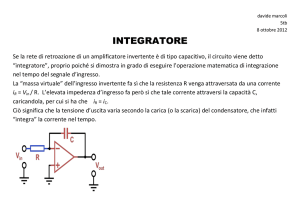
Circuito integratore
L’integratore è un altro esempio di circuito composto da un OP-AMP e
una rete di retroazione dipendente dalla frequenza. Nel circuito mostrato in
figura, il resistore R2 è sostituito da una condensatore. L’analisi può
essere condotta non solo nel dominio della frequenza, come fatto
precedentemente, ma anche nel dominio del tempo.
i
v(t)
c
vs
C
R
is
t
i-
+
vs
vo
(a)
(b)
vo
(a) The integrator circuit; (b) Output voltage for a
step-function input with vC(0) = 0
Poiché il terminale invertente rappresenta massa virtuale, si ha:
is = v s / R
e
ic = - Cdvo / dt
Poichè inoltre non vi è assorbimento di corrente all’ ingresso dell’OPAMP, dovrà essere is = ic . Quindi, uguagliando le relative espressioni e
integrando, si ottiene:
∫dvo = ∫ -1/RC vs d ovvero vo(t) =-1/RC ∫ vs () d + vo(0)
in cui il valore iniziale della tensione di uscita è determinato dalla tensione
del condensatore all’istante t=0. La tensione di uscita, quindi, è data dalla
somma della tensione iniziale sul condensatore e dall’integrale della
tensione d’ingresso.
Con il condensatore inizialmente scarico, si ha vo(0) = 0.
Questo circuito è un integratore di precisione di larga applicazione nei
generatori di funzioni, nei convertitori analogico/digitali, etc..
Esercizio: Si abbia come segnale d’ingresso un’onda quadra di frequenza
pari a 500 KHz, valore min e max rispettivamente di 0 e 10 V. si definisca
il valore di R e C per l’integratore in modo che il valore di picco della
tensione di uscita sia pari a 10 V e si abbia inoltre RIN = 10 K
Circuito derivatore
Scambiando il posto della resistenza e della capacità, si ottiene un circuito
dalle funzioni complementari, cioè un circuito che effettua la derivata del
segnale d’ingresso.
Infatti si ha:
vo/R = - Cdvs / dt
da cui risulta
vo = - RCdvs / dt
Current to Voltage Amplifier (Transimpedance Amplifier)
A circuit for converting small current signals (>0.01 microamps) to a more
easily measured proportional voltage.
By the current rule:
so the output voltage is given by the expression above.
Photodiode Light Detector
This light detector is a current-to-voltage
converter. The FET input op-amp prevents
the loading of the photodiode and the
voltage at the output is proportional to the
current in the photodiode. So long as the
photodiode response to the light is linear,
the output voltage is proportional to the
light falling on the photodiode.
Photodiodes
A photodiode consists of an active p-n junction which is operated in
reverse bias. When light falls on the junction, a reverse current flows
which is proportional to the illuminance. The linear response to light
makes it an element in useful photodetectors for some applications. It is
also used as the active element in light-activated switches.