Lezione 5

Università degli Studi del Piemonte Orientale
Corso di Laurea in Infermieristica
Corso integrato in Scienze della Prevenzione e dei Servizi sanitari
Statistica
Lezione 5
a.a 2011-2012
Dott.ssa Daniela Ferrante
[email protected]
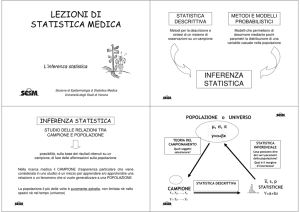
Inferenza statistica
L’inferenza statistica è un insieme di metodi con cui si
cerca di trarre una conclusione sulla popolazione sulla
base di alcune informazioni ricavate da un campione
estratto da quella popolazione.
Il percorso dell’inferenza statistica si svolge secondo le
seguenti fasi:
1. estrazione di un campione della popolazione
2. calcolo delle statistiche campionarie, cioè dei valori
corrispondenti ai dati contenuti nel campione
3. stima dei parametri nella popolazione in base ai risultati
forniti dal campione
2
Popolazione
Insieme che raccoglie tutte le osservazioni possibili,
relativamente ad una data variabile o ad un dato fenomeno.
Può essere finita (comunque molto grande) o infinita
3
Campione
- Raccolta finita di elementi estratti da una popolazione
- Scopo dell’estrazione è quello di ottenere informazioni
sulla popolazione
- Il campione deve essere rappresentativo
popolazione da cui viene estratto (‘non viziato’)
della
- Per corrispondere a queste esigenze il campione viene
individuato con un campionamento casuale.
4
In un campionamento casuale semplice tutti gli individui
nella popolazione hanno uguale probabilità di essere
inclusi nel campione.
individui nella popolazione = "unità di campionamento"
popolazione oggetto dello studio = "popolazione bersaglio"
popolazione effettivamente campionabile (al netto
dell'effetto di fattori di selezione) = "popolazione studio" o
base di campionamento
5
Distribuzione della media campionaria
Consideriamo tutti i possibili campioni casuali di ampiezza
n che possono essere estratti da una popolazione.
Per ciascun campione si può calcolare una statistica (es.
la media) che varia da campione a campione.
Possiamo dunque considerare la statistica in questione
come una variabile casuale e studiarne la distribuzione.
Se ad esempio la statistica usata è la media, la
distribuzione è detta distribuzione della media
campionaria.
Campionamento da popolazione distribuita normalmente
Se campioniamo da un popolazione normale allora:
• La distribuzione di
x (media campionaria) è normale
• La media delle medie campionarie corrisponde alla
media della popolazione (µ)
• La varianza della distribuzione della media campionaria
è uguale alla varianza della popolazione diviso per la
dimensione del campione
7
Campionamento da popolazione distribuita non
normalmente
• In questo caso introduciamo il teorema centrale limite:
Data una popolazione distribuita non normalmente, la
distribuzione della media campionaria calcolata da campioni
di dimensione n, avrà media µ e varianza σ2/n e, se la
dimensione campionaria è grande (un campione di
dimensione 30 è considerato soddisfacente), avrà
distribuzione pressochè normale
8
Esempio
Quale sarà la probabilità di osservare un soggetto con una statura
inferiore a m 1,5928 data una popolazione con altezza media
1,730 e deviazione standard 0,07 (distribuzione di partenza
assunta come normale)?
Si estragga un campione di ampiezza 10, calcolare la probabilità
che la media campionaria dell’altezza sia superiore a 1,65.
N.B Nel caso della media campionaria la standardizzazione
avviene nel seguente modo:
z=
x−µ
σ
n
9
Esempio
z =
z =
x − µ
σ
1,5928−1,73
P( x < 1,5928) = P(z <
) = P(z < −1,96) = 0,025
0,07
x − µ
P ( x > 1, 65 ) = P ( z >
σ
n
1, 65 − 1, 73
) = P ( z > − 3,7 ) ~
=1
0 , 07
10
0,6
0,4
0,2
0,0
X
-4
-3,7
-3
-2
-1
0
1
2
3
4
5
6
10
Stima puntuale e stima intervallare
Una stima puntuale è un procedimento attraverso il
quale a partire dalle informazioni tratte da un campione
si ottiene come risultato un singolo valore numerico
usato come stima del parametro dell’intera popolazione
Es. stima della media
xi
∑
x =
n
Una stima intervallare è un procedimento attraverso il
quale a partire dalle informazioni tratte da un campione
si ha come risultato un insieme di valori che con un
certo grado di fiducia conterrà il parametro da stimare
11
– Campioni ripetuti dalla stessa popolazione forniscono
medie campionarie diverse
– Ciascuna di queste medie campionarie costituisce una
stima non distorta del parametro (media della popolazione)
ma non può essere usata come stima del parametro da
sola, senza tenere conto dell’incertezza causata dall’errore
campionario
12
Stima intervallare della media campionaria
( x − z1−α / 2 *
σ
n
z1−α / 2
; x + z1−α / 2 *
σ
n
)
Coefficiente di attendibilità
Se α=0,05
0,95
0,025
0,025
-1,96
+1,96
13
Interpretazione dell’intervallo di confidenza
Estraendo tutti i possibili campioni da una popolazione
distribuita normalmente, il 95% degli intervalli conterrà la
media della popolazione ossia abbiamo un grado di
fiducia del 95% che la media della popolazione si trovi tra
i due valori estremi dell’intervallo
14
Esempio
La media della distribuzione della pressione sistolica
delle donne diabetiche di età compresa tra 30 e 34 anni
non è nota, tuttavia la deviazione standard è σ=11,8
mmHg. Un campione casuale di 10 donne è selezionato
da questa popolazione: la pressione sistolica media del
campione è pari a 130 mmHg.
Calcolare un intervallo di confidenza al 95% per la media
della popolazione
15
Esempio
( x − z1−α
/ 2
*
(130 − 1 , 96 *
σ
n
; x + z1−α
/ 2
*
σ
n
)
11 , 8
11 , 8
;130 + 1 , 96 *
)
10
10
(122 ,7 ;137 ,3)
16
La distribuzione t
William Sealey Gosset
Nel caso in cui non conosciamo la deviazione
standard della popolazione, possiamo ricorrere alla
deviazione standard campionaria. In questo caso
facciamo riferimento alla distribuzione t di Student.
Il t di Student è un test di statistica parametrica. E’
fondato sulle caratteristiche della distribuzione
normale.
17
La distribuzione t
– Ha media 0
– E’ simmetrica intorno alla media
– Rispetto alla distribuzione normale è meno appuntita
al centro e ha code più alte
– Tende alla distribuzione normale quando n è
sufficientemente grande
– E’ caratterizzata dai gradi di libertà che misurano la
quantità di informazione disponibile nei dati per
stimare σ2. Per ogni valore dei gradi di libertà c’è una
diversa distribuzione di t. All’aumentare dei gradi di
libertà la distribuzione della t si avvicina alla
distribuzione normale
18
Distribuzione normale (curva blu) e t di student per 1, 2, 3, 5, 10, 30
gradi di libertà
Grafici tratti da: http://en.wikipedia.org/wiki/Student's_t-distribution
19
Il procedimento per il calcolo dell’intervallo di confidenza
della media nel caso in cui sia necessario ricorrere alla
distribuzione t di Student è analogo al caso precedente ma
si sostituisce il valore di σ con il valore s
( x − t1 − α
s=
/2
*
s
; x + t1 − α
n
∑ ( xi − x ) 2
n −1
/2
*
s
)
n
Gradi di libertà = n-1
I gradi di libertà sono (n-1) poiché abbiamo perso 1 grado di
libertà per stimare la media
20
Esempio
• Riprendiamo l’esempio precedente supponendo di non
conoscere σ.
La media e la deviazione standard della distribuzione della
pressione sistolica delle donne diabetiche di età compresa tra
30 e 34 anni non è nota. Un campione casuale di 10 donne è
selezionato da questa popolazione: la pressione sistolica
media del campione è pari a 130 mmHg e la deviazione
standard campionaria pari a 20.
Calcolare un intervallo di confidenza al 95% per la media
della popolazione.
21
Esempio
( x − t1 − α
/2
s
*
; x + t1 − α
n
( 130 − 2 , 26 *
/2
s
*
)
n
20
20
;130 + 2 , 26 *
)
10
10
(115,70;144 ,30 )
t1−α / 2 = 2,26
0,5
0,95
0,4
0,3
0,2
0,1
0,0
T
-5
-4
-3
-2
-1
0
1
2
3
4
5
g.d.l = n-1 = 9; α=0.05
22
Distribuzione T
2 code
1 coda
Probabilità
0,005 0,010 0,025 0,050
0,010 0,020 0,050 0,100
gradi libertà
1 63,66 31,82 12,71 6,31
63,66 31,82 12,71 6,31
2 9,22 6,96 4,30 2,92
9,22 6,96 4,30 2,92
3 5,84 4,54 3,18 2,35
5,84 4,54 3,18 2,35
4 4,60 3,75 2,78 2,13
4,60 3,75 2,78 2,13
5 4,03 3,37 2,57 2,02
4,03 3,37 2,57 2,02
6 3,71 3,14 2,45 1,94
3,71 3,14 2,45 1,94
7 3,50 3,00 2,37 1,90
3,50 3,00 2,37 1,90
8 3,36 2,90 2,31 1,86
3,36 2,90 2,31 1,86
9 3,25 2,82 2,26 1,83
3,25 2,82 2,26 1,83
10 3,17 2,76 2,23 1,81
3,17 2,76 2,23 1,81
11 3,11 2,72 2,20 1,80
3,11 2,72 2,20 1,80
12 3,06 2,68 2,18 1,78
3,06 2,68 2,18 1,78
13 3,02 2,65 2,16 1,77
3,02 2,65 2,16 1,77
14 2,98 2,63 2,15 1,76
2,98 2,63 2,15 1,76
15 2,95 2,60 2,13 1,75
2,95 2,60 2,13 1,75
16 2,92 2,58 2,12 1,74
2,92 2,58 2,12 1,74
17 2,90 2,57 2,11 1,73
2,90 2,57 2,11 1,73
18 2,88 2,55 2,10 1,73
2,88 2,55 2,10 1,73
19 2,86 2,54 2,09 1,73
2,86 2,54 2,09 1,73
20 2,85 2,53 2,09 1,73
2,85 2,53 2,09 1,73
per numeri di g.l. superiori a 20 usate la riga corrispondente a 20
23