Teoria della rappresentazione dei grafici

Appunti del corso di Sistemi Elettronici – Prof. A. Celentano – a.s. 2005/2006
________________________________________________________________________________________________________________________
Teoria della rappresentazione dei grafici
Un grafico è un’appropriata rappresentazione di dati al fine di dare un’immediata comprensione dell’andamento che
essi rappresentano e per poter ricavare informazioni quantitative sul fenomeno che i dati stessi rappresentano. Facciamo
un esempio.
Se misuriamo la corrente (Ampere) che scorre in un resistore in funzione della
tensione (Volt) che si manifesta ai sui capi, otteniamo una serie di coppie di
valori (Vx,Ix) che se rappresentati su un diagramma cartesiano V-A ( leggi
tensione-corrente)
ci
danno
un’informazione sulla natura della legge
che lega le due variabili elettriche, cioè la
.
legge di Ohm V=R I. Tale grafico ci
permette di ricavare anche informazioni quantitative: ad una data corrente Ix che
attraversa il resistore corrisponde una ben precisa tensione ai suoi capi, la tensione
Vx che possiamo ricavare direttamente dal grafico.
Come altro esempio possiamo immaginare di voler rappresentare una data funzione
matematica, per esempio la funzione f(x)=3x2+2x+5. In questo caso, assegnando dei valori alla variabile X ricaviamo il
corrispondente valore della funzione. Ossia ricaviamo una serie di coppie [ x,f(x) ] che rappresentate graficamente ci
forniscono informazioni sulla natura della funzione (se è una retta, una parabole, un cerchio…) e sulla “prevedibilità”
della funzione stessa, qual’è il valore assunto dalla funzione in un dato punto x senza effettuare calcoli, ma leggendolo
dal grafico.
Dopo questi esempi si comprende che i “dati” devono essere rappresentati con un preciso criterio al fine di ricavarne
informazioni utili e precise. Per fare questo dobbiamo stabilire una precisa corrispondenza tra i nostri dati ed i punti
“grafici” che possiamo rappresentare su un foglio di carta. Come primo passo vediamo come si distribuisce in modo
preciso un insieme di dati su una retta (rappresentazione unidimensionale).
In matematica il teorema di Talete (o corrispondenze di Talete) ci permette di stabilire
una precisa corrispondenza lineare tra i dati “reali” che dobbiamo rappresentare
graficamente ed i punti “grafici”. Il teorema di Talete afferma che:
un fascio di rette parallele individua su due rette trasversali una serie di
segmenti proporzionali tra di loro.
Osserviamo il disegno riportato di seguito. La retta R rappresenta i valori “reali” che
vogliamo rappresentare sulla retta G, che è la retta delle rappresentazioni grafiche.
Supponiamo di avere tre punti Xa,Xb ed X sulla retta dei punti reali e per i quali
passano tre rette parallele che individuano tre punti corrispondenti sulla retta G, cioè
Ya, Yb ed Y. Supponiamo che valga la relazione d’ordine Xa < X < Xb e quindi anche
Ya< Y < Yb . Sulle due trasversali si individuano una serie di segmenti che sono
proporzionali tra di loro. In particolare possiamo scrivere:
Nella formula (X-Xa) è la lunghezza del segmento XXa. Scriviamo questa formula sotto forma di frazione e ricaviamo il
valore di Y. Dopo qualche calcolo, si ottiene:
Questa formula ci permette di rappresentare graficamente i dati. Infatti si vede che al punto reale X a, che è il minimo
dei dati da rappresentare, corrisponde i punto grafico Y a, che è il minimo punto sul nostro grafico (basta sostituire alla
X il valore Xa). Allo stesso modo, il dato reale Xb, che è il punto di massimo, corrisponde Yb che è il punto grafico
massimo.
Per fissare le idee, facciamo un semplice esempio. Supponiamo di aver fatto delle misure e quindi di dover
rappresentare su una retta il seguente insieme di valori.
{ 12 ; -7,3 ; -1 ; 4,9 ; 13,7 }
La prima cosa da fare è determinare i punti di minimo e massimo. Nel nostro caso si ha Min=-7,3 e Max=13,7 . Questi
corrispondono ai valori Xa e Xb. Supponiamo di voler rappresentare questi valori su un segmento lungo 97mm, per cui
Ya=0 e Yb=97. Di ciascun valore X riportato sopra calcoliamo il corrispondente valore Y sul grafico. E cioè,
rispettivamente, si ha: { 89mm ; 0mm ; 29mm ; 56mm ; 97mm }
Pag. 1
Appunti del corso di Sistemi Elettronici – Prof. A. Celentano – a.s. 2005/2006
________________________________________________________________________________________________________________________
Riportiamo questi valori su una retta graduata (in millimetri). Otteniamo:
Da quest’immagine si vede la giusta distribuzione dei valori reali sull’asse grafico. Si osservi come il minimo dei dati
coincide con l’inizio del grafico e il massimo dei dati coincide con il punto di massima lunghezza del segmento.
La teoria esposta ci permette di rappresentare dei “dati” in una dimensione, appunto sulla retta. Nel caso di
rappresentazioni bidimensionali, sul piano, dobbiamo applicare il metodo due volte: una volta per l’asse X ed un’altra
volta per l’asse Y. Solo in questo modo possiamo essere certi di eseguire una rappresentazione dei dati che sia corretta e
precisa.
Alcune osservazioni.
1) In genere sia per l’asse delle ascisse che per l’asse delle ordinate si deve prendere una stessa unità di misura.
Ciò viene fatto prendendo uno stesso segmento e dividendolo in uno stesso numero di parti.
2) Se un gruppo di dati, quello da rappresentare sull’asse X o sull’asse Y, è numericamente molto alto, tipo 20314
oppure 315000, conviene determinare un fattore numerico che ci permette di ottenere numeri più piccoli.
Nell’esempio appena fatto conviene dividere tutti i numeri per 10000 ed eseguire i relativi calcoli di
rappresentazione. In questo caso vicino all’asse di rappresentazione si riporta il fattore di divisione 1/10000.
3) Se l’insieme dei dati da rappresentare sono numeri relativi, positivi e negativi, nella rappresentazione grafica si
deve sempre indicare la posizione dello zero.
Gli istogrammi
Questi tipi di grafici sono usati per rappresentare non i dati veri e propri ma delle fasce di dati. Per fissare le idee,
supponiamo di avere a disposizione un centinaio di dati che dobbiamo rappresentare in un grafico. In questo caso i dati
non possono essere rappresentati graficamente per le ovvie difficoltà di rappresentazione: è complesso e faticoso
riportare 100 dati su un grafico. Conviene raggruppare tutti i dati in modo che ogni gruppo contenga dei dati più o meno
dello stesso ordine di grandezza. In questo modo si rappresenteranno le frequenze con cui i dati cadono nei vari gruppi.
Per frequenza intendiamo il numero dei dati che cadono in un dato raggruppamento. Nel nostro esempio, supponiamo
che i dati sono numeri compresi tra 0 e 100. In questo caso individuiamo 10 raggruppamenti o fasce di dati: la fascia 1
contiene i numeri tra 0 e 10; la fascia 2 contiene i dati compresi tra 11 e 20; ecc. ecc. Osserviamo la tabella riportata di
seguito, sono riportate le frequenze con cui i dati cadono nelle varie fasce: sono queste frequenze i dati che
rappresentiamo in un istogramma. Costruiamo l’istogramma.
Su un foglio riportiamo un segmento più o meno lungo a piacere. Dividiamolo in un numero di parti pari al numero di
raggruppamenti fatti. Nel nostro esempio 10 parti. Ogni parte rappresenta la base di un rettangolo la cui altezza è
proprio il numero espresso dalla frequenza relativa ad una data fascia. Qui di seguito è riportato sia la tabella dei dati da
rappresentare che il relativo istogramma.
Spesso sulla sommità del rettangolo che rappresenta la frequenza dei dati per quel raggruppamento è riportato il valore
percentuale che quel raggruppamento rappresenta. Il primo raggruppamento rappresenta l’8 %, poiché sono 8 dati su
100 che cadono nel primo raggruppamento; il secondo raggruppamento rappresenta il 2 %.
Pag. 2
Appunti del corso di Sistemi Elettronici – Prof. A. Celentano – a.s. 2005/2006
________________________________________________________________________________________________________________________
Gli aerogrammi (diagrammi a ‘torta’)
Questi diagrammi sono usati quando si hanno pochi numeri da rappresentare e si vuole vedere graficamente il rapporto
quantitativo esistente tra i dati. Supponiamo di avere il seguente campione di dati:
30 ; 70 ; 85 ; 43 ; 105
In questo caso la rappresentazione viene fatta dividendo un cerchio (la torta!) in parti tali da mantenere il rapporto
percentuale dei dati. Il rapporto percentuale dei dati si calcola sommando tutti i dati e dividendo ciascun dato per questa
somma. La somma dei dati è 333, come si può verificare. Il rapporto percentuale del primo dato è (30/333)x100=9%.
Allo stesso modo, per il secondo dato, (70/333)x100=21%. Il rapporto percentuale di tutti i dati è il seguente:
9% ; 21% ; 26% ; 13% ; 31%
La rappresentazione di queste percentuali si ottiene dividendo l’area del cerchio
nelle stesse percentuali. Oppure si calcolano gli angoli al centro del cerchio che
corrispondono alle stesse percentuali. Per il primo dato da rappresentare, cioè 30, e
cioè 9% si ha un angolo pari a: 360°x9/100=32°. Per il secondo dato:
70→21%→360°x21/100=75°. In definitiva otteniamo i seguenti angoli:
32° ; 75° ; 74° ; 47° ; 132°
Chiaramente resta ora il problema di rappresentare questi angoli nel cerchio. I casi
sono due:
a) si può usare un goniometro e si tracciano consecutivamente tutti gli
angoli;
b) si individuano gli angoli con una precisione più o meno accettabile, dato
che sappiamo tracciare angoli di 90°, 45°, 22.5° e 11°.
Ciascuna area individuata deve essere colorata o tratteggiata in modo da renderla ben distinta dalle altre aree. Si veda il
grafico riportato a lato. All’interno delle aree così individuate, in genere, vanno indicati i valori dei dati che esse
rappresentano, non va assolutamente indicato il valore dell’anglo che tracciato e tanto meno il valore percentuale che
l’area rappresenta.
Rappresentazioni in scala logaritmica.
Spesso nasce la necessità di dover rappresentare in un grafico un’insieme di numeri molto diversi tra loro per
dimensione numerica. Per intenderci, se volessimo rappresentare la banda passante di un filtro audio dobbiamo poter
riportare in un grafico sia numeri “piccoli” del tipo 10 Hz, 100 Hz, sia numeri relativamente più grandi, del tipo 20000
Hz, 30000 Hz. Di conseguenza si comprende la difficoltà di riportare in un grafico numeri molto diversi tra loro per
grandezza numerica e, quindi, male si prestano ad essere trattati con un metodo proporzionale descritto in precedenza.
In questi casi si opera un’espediente “tecnico”: invece di riportare nel grafico i valori dei dati da rappresentare si
riportano i logaritmi di dati stessi. In questo modo, per esempio, dovendo riportare il numero 100 ed il numero 30000
riporteremo nel grafico i valori Log(100), che è 2, e Log(30000), che vale 4.4, cioè numeri più o meno simili per
grandezza.
Il logaritmo è una funzione che viene introdotta nel corso di matematica. Qui ci limiteremo solo alla sua applicazione
pratica. Dato un numero positivo, per esempio 12700, il logaritmo di questo numero è Log(12700) = 4.1038, ottenuto
con una banalissima calcolatrice scientifica tascabile. Questo numero significa che se facciamo 10 4.1038 viene giusto
12700. Questi sono i logaritmi decimali, decimali perché si usa la base 10 nella potenza. Sulle calcolatrici è riportato
anche un altro tipo di logaritmo indicato con ln, che sta per logaritmo naturale o in base e. Il numero e, o numero di
Nepero, vale 2.7182. In seguito ci riferiremo solo ai logaritmi decimali. Dopo questa considerazione si comprende che
nel graficare dei dati in luogo di rappresentare i dati stessi possiamo considerare di rappresentare i logaritmi di questi,
visto che con una semplice trasformazione matematica si può passare dagli uni agli altri.
Pag. 3
Appunti del corso di Sistemi Elettronici – Prof. A. Celentano – a.s. 2005/2006
________________________________________________________________________________________________________________________
Vediamo adesso come è fatto un foglio di carta squadrato in scala logaritmica. Su un foglio di carta si riportino gli assi
cartesiani ortogonali. Supponiamo che l’ascissa dovrà contenere la scala logaritmica. Sull’ascissa si individuano tanti
segmenti tutti uguali e con ampiezza a piacere. Come si vede dalla
figura qui a lato. Poiché vogliamo una scala logaritmica, lo zero
indicherà l’inizio di un segmento che conterrà i
valori maggiori di 100=1. Mentre il riferimento 1
indicherà il limite entro cui inserire tutti i valori al di
sotto di 101=10. Il riferimento 2 indicherà il limite
entro cui mettere i valori al di sotto di 102=100, mentre il 3 indicherà il limite di 103=1000, ecc. ecc.
Ogni segmento deve essere diviso in decade, cioè in 10 parti. Dobbiamo riportare le suddivisioni
contrassegnate dai numeri 1,2,3,4,5,6,7,8,9 che ci permetteranno di dividere il segmento in 10 parti.
Queste suddivisioni non devono essere di tipo lineare,cioè non dobbiamo dividere il segmento in
parti uguali, ma dobbiamo considerare che riporteremo i valori logaritmi. Per cui dobbiamo riportare
linearmente non i numeri 1,2,3,4… ma bensì i logaritmi, cioè log(1), log(2), ecc. ecc. Costruiamo la
tabella riportata qui a lato. Graficamente, in modo proporzionale, riportiamo i valori dei logaritmi
presenti nella tabella. Otterremo la figura seguente, che mostra un foglio squadrato in scala semi-logaritmica, perché la
scala logaritmica è applicata all’asse X e mentre sull’asse Y abbiamo lasciato la scala lineare. Se la scala logaritmica
viene applicata sia all’asse X che all’asse Y allora la rappresentazione si
dice che è in scala bi-logaritmica o semplicemente in scala logaritmica.
Vediamo di fare qualche esempio concreto che ci permetta tanto di
costruire un grafico che di leggerlo.
Vediamo prima come si legge un grafico in scala logaritmica.
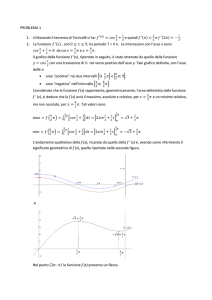
Osserviamo il grafico riportato qui di seguito. Rappresenta la banda
passante di un filtro audio, un tipo di grafico che si trova spesso nei
manuali di elettronica. Sull’asse delle ascisse sono riportate le
frequenze del segnale in Hz in scala logaritmica. Sul grafico sono stati
segnati alcuni punti,A, B, C …, leggiamo le frequenze in questi punti.
Il punto A si trova segnato sulla terza linea verticale, che è la linea dei
4/10, per cui il valore di frequenza è: 100.4=2.5Hz.
Vediamo a che frequenza si trova il punto B. In questo
caso il punto è situato dopo la prima decade in
corrispondenza di 1+2/10=1.2 e pertanto il valore della
frequenza è 101.2=16Hz.
Il punto C si trova ad 1.9 e per cui la frequenza è
101.9=80Hz. Il punto D è alla frequenza 102.7=500Hz ed
il punto E si trova alla frequenza 103.3=2000Hz=2KHz.
Si osservi come dal grafico è possibile ottenere
informazioni sulle basse frequenze, punti A e B, ed
anche contemporaneamente sulle alte frequenza, i punti
D ed E. Ovviamente quando leggiamo dal grafico dei
valori questi non sono precisi, ma vanno intesi sempre nell’ambito di un errore. Ciò è dovuto al fatto che abbiamo
voluto rappresentare numeri molto diversi tra loro.
Si osservi che sull’asse delle ascisse sono state indicate
le decade progressive, ciò non toglie che possono essere
indicati direttamente i valori, come si osserva dalla
figura qui a lato in cui sull’ascissa sono riportati i valori
in Hertz.
Vediamo adesso di costruire un grafico in scala
semilogaritmica. Dall’esposizione appena conclusa si
comprende che riportare dei dati su un foglio in scala
semilogaritmica è molto semplice: basta calcolare il
logaritmo di ogni dato e, limitandosi alla prima cifra decimale, collocarlo nella giusta posizione sul foglio. Per esempio
se dobbiamo riportare il punto 12300, calcoliamo il logaritmo che è 4.089 e, quindi, sul foglio in scala semilogaritmica
segniamo un punto nella quarta decade. Se dobbiamo riportare il valore di 3200, il logaritmo è 3.5 per cui il punto va
segnato nella terza decade sulla quinta linea verticale, che rappresenta 5/10.
Pag. 4
Appunti del corso di Sistemi Elettronici – Prof. A. Celentano – a.s. 2005/2006
________________________________________________________________________________________________________________________
Pag. 5