U NIVERSIT À DEGLI S TUDI DI P ISA
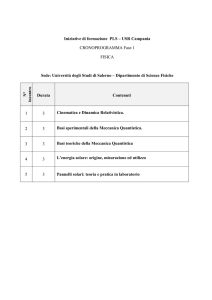
FACOLT À
DI
S CIENZE M ATEMATICHE , F ISICHE E N ATURALI
C ORSO DI L AUREA IN F ISICA
A NNO A CCADEMICO 2006/2007
E LABORATO F INALE
L’integrale di Feynman e applicazioni alla
meccanica quantistica
Candidato
Daniele Somensi
Relatore
Prof. Kenichi Konishi
Indice
Introduzione
5
1
L’integrale sui cammini
1.1 Costruzione . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 La particella libera . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Il limite classico . . . . . . . . . . . . . . . . . . . . . . . . . .
7
7
9
9
2
Formulazione euclidea
2.1 Il tempo immaginario . . . . . . . . . . . . . . . . . . . . . . .
2.2 L’oscillatore armonico . . . . . . . . . . . . . . . . . . . . . .
11
11
12
3
Sviluppi perturbativi
3.1 Preliminari algebrici . . . . . . . . . . . . . . . . . . . . . . .
3.2 L’oscillatore armonico perturbato . . . . . . . . . . . . . . . .
15
15
18
4
Topologia e meccanica quantistica
4.1 La particella in moto circolare . . . . . . . . . . . . . . . . . .
4.2 L’effetto di Aharonov-Bohm . . . . . . . . . . . . . . . . . . .
21
21
23
5
Gli istantoni
27
3
4
INDICE
Introduzione
Verso la fine degli anni ’40, Feynman presentò una formulazione alternativa della meccanica quantistica. L’idea che sta alla base dell’integrale feynmaniano sui cammini è che l’ampiezza di probabilità per un deteminato
processo, è data dalla somma di tutti i possibili modi differenti in cui tale
processo può realizzarsi. L’approccio di Feynman può essere enunciato
nei seguenti postulati:
• La probabilità che ha una particella di arrivare ad un punto q1 al tempo t1 partendo da q0 al tempo t0 è il modulo quadro di un’ampiezza
G(q1 , t1 ; q0 , t0 ) di andare da (q0 , t0 ) a (q1 , t1 ).
Questa ampiezza è la somma di tutti i contributi φ(x(t)), calcolati per
ogni cammino che parte da (q0 , t0 ) e arriva a (q1 , t1 ).
X
G(q1 , t1 ; q0 , t0 ) =
φ(x(t))
tutti i
cammini
• il contributo del cammino φ(t) è dato da
φ(x(t)) = AeiS[x(t)]/~
Dove S[x(t)] è l’azione classica del sistema per il cammino x(t) e ~ è
la costante di Planck ridotta.
La funzione G (la funzione di Green) è chiamata funzione di correlazione
o anche propagatore.
I vantaggi della formulazione di Feynman sono molti, anche se in meccanica quantistica non fornisce nuovi risultati. Prima di tutto fornisce un’interpretazione intuitiva della meccanica quantistica ed il limite classico può
essere ricavato in modo molto pulito.
Inoltre permette di sviluppare metodi sistematici per lo studio dei fenomeni
perturbativi (utilizzando i grafici di feynman).
Il path integral gioca un ruolo importante nella teoria dei campi, sia relativistica che non relativistica. Molti metodi sviluppati per la meccanica quantistica possono essere generalizza alla teoria dei campi. La Lagrangiana è un’invariate di Lorentz (a differenza dell’Hamiltoniana), questo
5
6
INDICE
è un considerevole vantaggio nella teoria dei campi relativistica.
Utilizzando il Path Integral gli istantoni possono venire introdotti in modo
naturale e utilizzati per studiare fenomeni non perturbativi (come l’effetto
tunnel in meccanica quantistica o il confinamento del colore in cromodinamica quantistica).
Capitolo 1
L’integrale sui cammini
1.1
Costruzione
Consideriamo un sistema quantistico descritto dall’Hamiltoniana H. La
sua funzione di Green sarà
A ≡ K(q 0 , T ; q, 0) = q 0 e−iHT |qi .
(1.1)
Inserendo un fattore 1 nella forma di somma su tutti gli autostati della
posizione si ottiene
A = q 0 e−iH(T −t1 ) e−iHt1 |qi = q 0 e−iH(T −t1 )
Z
dq1 |q1 i hq1 | e−iHt1 |qi=
|
{z
}
=1
Z
dq1 K(q 0 , T ; q1 , t1 )K(q1 , t1 ; q, 0).
(1.2)
Questa non è altro che la proprietà di convoluzione della funzione di
Green o la proprietà di addizione delle ampiezze di probabilità.
Possiamo ripetere la divisione dell’intervallo temporale T in n parti di
durata δ = T /N . La funzione di Green diventa
N
−iHδ
A = q 0 e−iHδ
|qi = q 0 e|−iHδ e−iHδ
{z · · · e
} |qi .
(1.3)
N volte
Possiamo inserire un set completo di autostati tra ogni esponenziale,
ottenendo
Z
A=
dq1 dqN −1 KqN ,qN −1 · · · Kq1 ,q0
7
(1.4)
8
CAPITOLO 1. L’INTEGRALE SUI CAMMINI
Figura 1.1: Ampiezza come somma su i cammini a N lati
Dove Kqi,qi+1 = hqi | e−iHδ |qi+1 i è il propagatore infinitesimo. Questa espressione ci dice che l’ampiezza è l’integrale dell’ampiezza di tutti i
cammini con N lati, come illustrato in figura 1.1
Possiamo sviluppare l’esponenziale:
Kqj+1 ,qj = hqj+1 | e−iHδ |qj i = hqj+1 | qj i − iδ hqj+1 | H |qj i + o(δ 2 )
(1.5)
2
p
Ora consideriamo un Hamiltoniana del tipo H = 2m
+ V Possiamo riscrivere il propagatore infinitesimo come
Z
dpj ipj (qj+1 −qj ) −iδH(pj ,q̄j )
Kqj+1 ,qj =
e
e
(1 + o(δ 2 )).
(1.6)
2π
(q
−q )
Se definiamo q̇j = j+1δ j possiamo riscrivere il propagatore totale (i.e. la
funzione di Green) come
Z NY
Z NY
−1
−1
N
−1
X
dpj
K=
dqj
exp iδ
(pj q̇j − H(pj , q̄j )) .
2π
j=0
j=0
j=0
Gli integrali in pj sono gaussiani e possono essere svolti esplicitamente
−1
N
−1
m N/2 Z NY
X
dqj exp iδ
K=
2πiδ
j=1
j=0
!
mq̇j2
− V (q̄j ) .
2
(1.7)
L’argomento dell’esponenziale è un’approssimazione discreta dell’azione
di un cammino che passa per i punti q0 = q, q1 · · · qN = q 0 . Prendendo il
1.2. LA PARTICELLA LIBERA
9
limite per N → ∞ si ottiene la funzione di Green scritta come somma su
tutti i cammini
Z
K = Dq(t)eiS[q(t)] .
(1.8)
1.2
La particella libera
Un caso in cui si può calcolare esplicitamente la funzione di Green utilizzando la definizione di Path Integral è quello della particella libera. Sia
H = p2 /2m l’Hamiltoniana della particella libera. Utilizzando la formula
1.7 otteniamo
−1
N −1 m N/2 Z NY
mδ X qj+1 − qj 2
K = lim
dqj exp i
N →∞ 2πiδ
2
δ
j=1
j=0
Gli integrali sono gaussiani e possono essere valutati ricorsivamente
utilzzando la nota identità
Z
∞
du
−∞
a 12
π
e−a(x−u)
2
21
21
2
b
ab
ab
(x − y)2
e−b(y−u) =
exp −
π
π(a + b)
a+b
(1.9)
Applicando N volta l’identità 1.9 si ottiene un risultato che dipende
solo dal punto iniziale e quello finale e non da N .
r
m
im
2
K(x, t; y, o) =
exp
(x − y)
2πit
2t
Dove si può notare che l’argomento dell’esponenziale è semplicemente
l’azione classica.
1.3
Il limite classico
É interessante ricavare il limite classico nella formulazione del Path Integral
Consideriamo due cammini vicini q(t) e q 0 (t) che contribuiscno al PI. Sia
q 0 (t) = q(t)+η(t) con η(t) piccolo. Possiamo sviluppare l’azione con Taylor
(funzionale)1 :
Z
δS[q]
0
S[q ] = S[q + η] = S[q] + dt η(t)
+ o(η 2 ).
δq(t)
1
L’unica proprietà che serve conoscere della derivata funzionale è: δq(t)/delta(t0 ) =
δ(t − t0 ), dove l’ultima δ è la Delta di Dirac. Per una definizione formale ed altre proprietà
si può vedere [2]
10
CAPITOLO 1. L’INTEGRALE SUI CAMMINI
Figura 1.2: I cammini vicino al cammino classico interferiscono
costruttivamente.
I due cammini danno un contributo exp[iS[q]/~] exp[iS[q 0 ]/~] al PI; il contributo totale dei due cammini sarà
Z
i
δS[q]
dt η(t)
,
K ' eiS[q]/~ 1 + exp
~
δq(t)
dove abbiamo trascurato le correzioni dell’ordine di η 2 . Si vede che la differenza di fase tra
R i due cammini, che determina l’interferenza tra i due
contributi, è ~−1 dtη(t)δS[q]/δq(t).
La differenza di fase cresce al diminuire di ~. Cosı̀ anche se i cammini sono
molto vicini, in modo tale che l’azione sia molto simile, per ~ abbastanza
piccolo la differenza di fase è anora grande, ed in media avviene c’è interferenza distruttiva.
Quest discorso deve essere modificato per un cammino eccezionale: quello
che realizza un estremo dell’azione, cioè, utilizzando il Principio di minima azione, la traiettoria classica, qc (t). Per questo cammino la variazione
dell’azione al prim’ordine è zero, δS = 0. Perciò per cammini vicini a quello classico si avrà un’interferenza costruttiva. Questo ci porta a concludere
che se il problema è classico (azione ~), il contributo più rilevante al PI
è dato dai cammini vicini a quello classico.
Capitolo 2
Formulazione euclidea
2.1
Il tempo immaginario
Se consideriamo il tempo immaginario (i.e. una continuazione analitica del
tempo) t = −iτ con τ ∈ R. Possiamo definire il propagatore euclideo
−H(τ1 −τ0 )
KE = hq1 | e
Z
q(τ1 )=q1
|q0 i =
[Dq]e−SE
(2.1)
q(τ0 )=q0
R
R
Dove SE = dτ LE = dτ mq̇ 2 + V (q) è l’azione euclidea. Si può notare che l’azione euclidea non è altro che l’azione standart con il potenziale
cambiato di segno.
Se in KE inseriamo un set completo di autostati di H si ottiene
X
X
X
KE = hq1 |
|ni hn|e−H(τ1 −τ0 )
|ni hn|q0 i =
ψn (q1 )ψn∗ (q0 )e−En (τ1 −τ0 )
n
n
n
Prendendo τ1 = −τ0 = τ e facendo il limite per τ → ∞, la somma è
dominata dal termine con n = 0, i.e. lo stato fondamentale.
Tramite
questa
P
Pnuova definizione è possibile La funzione di partizione
Z = j e−βEj = j hj| e−βH |ji può essere riscritta attraverso il Path Integral nella formulazione euclidea.
Infatti se integriamo il propagatore rispetto al punto iniziale
Z
Z
X
dq K(q, −iβ; q, 0) =
e−βEj hj| dq |qi hq| |ji = Z
j
|
{z
}
=1
Ricordando la definizione dell’azione euclidea si ottiene
Z
Z(β) = Dq(τ )e−SE (q)
Con le condizioni al bordo periodiche q(0) = q(β)
11
(2.2)
12
CAPITOLO 2. FORMULAZIONE EUCLIDEA
2.2
L’oscillatore armonico
Come applicazione della formulazione euclidea ricaviamo il propagatore
per l’oscillatore armonico.
2
2 2
La lagrangiana euclidea del problema è LE = q̇2 + ω 2q .
Z
−Hτ0
hq1 | e
|q0 i = N Dqe−SE
(2.3)
Dove SE è l’azione euclidea.
Definiamo q(τ ) = qcl (τ ) + δq(τ ) Dove qcl è la traiettoria euclidea classica e
E
perciò soddisfa δS
δqcl = 0 (i.e. realizza un minimo dell’azione euclidea). La
traiettoria classica soddisfa le equazioni del moto dell’oscillatore armonico
con il potenziale cambiato di segno. Prendiamo le condizioni al contorno
qcl ( −τ2 0 ) = q0 e qcl ( τ20 ) = q1 .
Possiamo riscrivere l’azione nella seguente forma
1
SE (qcl + δq) = SE (qcl ) +
2
Z
d2
00
dτ δq − 2 + V (qcl ) δq
dτ
(2.4)
Dove abbiamo usato che l’azione non ha termini lineari e che la lagrangiana
è quadratica.
A questo punto conviene sviluppare
la deviazione
δq utilizzando come
h
i
2
d
00
base gli autostati dell’operatore − dτ
2 + V (qcl )
δq(τ ) =
X
cn qn (τ )
(2.5)
n
Nel nostro caso scegliamo le comode condizioni al contorno q1 = q0 = 0.
In questo caso esiste una soluzione ovvia per qcl : qcl (τ ) = 0.
d2
2
− 2 + ω δqn = n δqn
dτ
Con le condizini al contorno qn (τ0 /2) = qn (−τ0 /2) = 0 gli autostati del nostro operatore diventano gli autostati di una buca di potenziale di altezza
infinita. Gli autostati e gli autovari sono perciò
(
n − ω 2 = π 2 n2 /τ02 ≡ λ2n
δqn = An sin[λn (τ + τ0 /2)]
Sfruttando l’ortonormalità degli autostati otteniamo per l’azione
SE = SE.cl +
1X
n c2n
2 n
(2.6)
2.2. L’OSCILLATORE ARMONICO
13
Sostituendo la 2.6 nella 2.3 si ottiene
R
Dqe−SE
=
N e−Scl
=N
RQ
− 12
n dcn e
P
n c2n
Q π2 n2 − 12 Q τ02
n
n
=N
Q∞ n=1
− 1
2
2
2
ω τ
1+
ω2
+
π 2 n2
τ02
− 1
2
0
π 2 n2
Se si pone V = 0 (i.e. ω = 0) nell’ultimo membro dell’equazione precedente rimane solo la prima produttoria. Cioè la prima produttoria è il
propagatore per la particella libera (particella in assenza di potenziale).
1
N
Y π 2 n 2 − 2
n
τ02
2 τ /2
0
= h0| e−p
|0i = √
1
2πτ0
La seconda produttoria si calcola ricordando il limite notevole
∞
Y
sinh(πy)
y2
=
n2
πy
1+
n=1
Rimmettendo insieme tutti i pezzi troviamo la forma finale del propapagatore per l’oscillatore armonico
1
K=√
2π
sinh(ωτ0 )
ω
− 1
2
Se prendiamo il limite per τ0 → ∞ otteniamo
K→
ω 1
2
π
e−ωτ0 /2
Che è della forma e−E0 τ0 |ψ0 (0)|2 dove E0 e ψ0 sono rispettivamente
autovalore e autostato dello stato fondamentale dell’oscillatore armonico.
14
CAPITOLO 2. FORMULAZIONE EUCLIDEA
Capitolo 3
Sviluppi perturbativi
3.1
Preliminari algebrici
Saremo nel seguito interessati a calcolare dei particolari integrali gaussiani.
Come preliminare algebrico studieremo gli analoghi integrali su Rn .
Z
1
Rn
dx1 · · · dxn xh1 · · · xhk e− 2 hx,Axi+U (x)
k∈N
h1 , · · · , hn ∈ {1, · · · , n}
(3.1)
Per gli integrali in Rn abbiamo i seguenti risultati elementari 1 :
Z
− 12 hAx,xi
Z0 =
dx e
=
Rd
Z
Zb =
1
A
det
2π
1
− 1
2
.
−1 bi
dx e− 2 hAx,xi+hb,xi = Z0 e 2 hb,A
.
Rd
Dove A è una matrice e x un vettore.
A questo punto è utile definire la funzione a m punti (o m-point)
Definizione 3.1.1 (m-point).
1
hf1 , f2 , . . . , fm i =
Z0
Z
1
dx e− 2 hAx,xi f1 (x) . . . fm (x).
Si può notare che la funzione a m punti delle coordinate verifica la
seguente identità
hxi1 , . . . , xim i =
1
1
−1 ∂i1 . . . ∂im Zb b=0 = ∂i1 . . . ∂im e 2 hb,A bi b=0
Z0
(3.2)
1
Se A è una matrice simmetrica basta diagonalizzarla e utilizzare l’invarianza del determinante per cambiamento di base. Mentre si può verificare che la parte antisimmetrica da
un contributo nullo
15
16
CAPITOLO 3. SVILUPPI PERTURBATIVI
Per funzioni qualsiasi possiamo svilippurle in serie di Taylor ottenendo
1
∂
∂
−1 bi hb,A
. . . fm
e2
hf1 , f2 , . . . , fm i = f1
(3.3)
∂b
∂b
b=0
Svolgendo le derivate nella 3.2 si ottiene un risultato fondamentale 2 :
Teorema 3.1.2 (Wick).
∂i1 . . . ∂im e
1
hb,A−1 bi
2
(P
b=0
=
0,
−1
A−1
j1 j2 . . . Ajm−1 jm ,
m = 2n
m = 2n + 1
Dove la somma è estesa a tutte le partizioni (j1 , j2 ), · · · , (jm−1 , jm ) in coppie
dell’insieme i1 · · · im di indici
Il teorema di Wick si può estendere per linearità a funzioni lineari arbitrarie,
Teorema 3.1.3 (Wick generalizzato).
X
hf1 , f2 , . . . , fm i =
hfi1 , fi2 i · · · hfim−1 ,fim i
(3.4)
dove la somma è estesa a tutte le coppie e la funzione a due punti hfj , fk i è data da
hfj , A−1 fk i
É conveniente rappresentare le funzioni a due punti nella formula 3.4
con un grafo. Consideriamo m punti, con il k-esimo punto che rappresenta
fk . Una partizione in coppie di 1, · · · , 2n fornisce un modo naturale per
connettere questi punti con n spigoli. Uno spigolo e = (j, k) rappresenta
−1
A−1
e = hfj , A fk i. L’equazione 3.4 diventa
X
Y
hf1 , . . . , fm i =
A−1
(3.5)
e ,
Γ e∈Spigoli(Γ)
Dove la somma è estesa a tutti i grafi univalenti (cioè i grafi tali che in ogni
vertice arriva solo uno spigolo).
I risultati trovati sopra possono essere generalizzati aggiungendo un
potenziale U (x). Definiamo ZU come
Z
1
ZU = dx e− 2 hAx,xi+λU (x)
Applicando la 3.3 con f = e(x) otteniamo:
∂
1
−1 bi
ZU = Z0 eλU ( ∂b ) e 2 hb,A
2
Per i calcoli espliciti si veda [3]
b=0
3.1. PRELIMINARI ALGEBRICI
17
Figura 3.1: I grafi del second’ordine
Il potenziale cubico
Consideriamo
ora l’importante esempio di un potenziale cubico
P
U (x) = Uijk xi xj xk . Calcoliamo l’espansione della funzione di partizione
ZU in serie λ.
Il coefficiente di λn è
n
1
Z0 X
−1
Uijk ∂i ∂j ∂k e 2 hb,A bi n!
i,j,k
b=0
Cominciamo con il coefficiente del termine di grado minore. Per il
terorema di Wick, il coefficiente di λ è nullo, mentre quello di λ2 è
1
Z0 X X
−1 Uijk Ui0 j 0 k0 ∂i ∂j ∂k ∂i0 ∂j 0 ∂k0 e 2 hb,A bi b=0 =
2!
0 0 0
i,j,k i ,j ,k
X
Z0 X X
Uijk Ui0 j 0 k0
Ai1 i2 Ai3 i4 Ai5 i6 , (3.6)
2!
0 0 0
i,j,k i ,j ,k
coppie
Dove l’ultima somma è su tutte le partizioni in coppie di i, j, k, i0 , j 0 , k 0 .
Possiamo ancor rappresentare queste partizioni attraverso grafi, connettendo sei vertici etichettati con i, j, k, i0 , j 0 , k 0 attraverso 3 spigoli che rappresentano Ai1 i2 Ai3 i4 Ai5 i6 . Per rappresentare il termine aggiuntivo Uijk
graficamente uniamo insieme la tripla (i, j, k) di vertici unialenti in un vertice trivalente; per preservare le etichettature, possiamo scriverle alla fine
degli spigoli che si incontrano in questo nuovo vertice. Allo stesso modo
rappresentiamo Ui0 j 0 k0 . Per ogni delle 6!/(23 3!) = 15 partizioni otteniamo
un grafo con due vertici trivalenti; abbiamo 6 coppie del grafo θ e 9 coppie
del grafo a manubrio (vedi figura 3.1).
Per il coefficiente di λn basta considerare la somma sui grafi trivalenti con
n vertici.
Per un potenziale U (x) generale bisogna svilupparlo in serie di Taylor; il
k-esimo termine sarà rappresentato da grafi k-valenti.
18
CAPITOLO 3. SVILUPPI PERTURBATIVI
3.2
L’oscillatore armonico perturbato
Consideriamo un potenziale V = 12 ω 2 q 2 + VI (q) dove VI è esprimibile in
serie di potenze VI = λq 3 + gq 4 . . ..
Come fatto per il potenziale cubico nella sezione precedente, Raggiungiamo
un termine di sorgente all’azione dell’oscillatore SE → SE + dτ J(τ )q(τ ).
Invece delle derivate parziali in questo caso si usano le derivate funzionali
che verificano l’identità
δ
φ(y) = δ(x − y)
δφ(x)
(3.7)
Si ottiene la seguente espressione per il propagatore euclideo, calcolato
prendendo come punto iniziale e finale l’origine ai tempi ±τ /2
Z
δ
−τ0
τ0
0
; 0,
= exp − dτ VI
KE [J] KE 0, −
.
2
2
δJ
J=0
Dove KE0 [J] è il propagatore euclideo dell’oscillatore armonico imperturbato con il termine di sorgente
KE0 [J]
Z
=
Z
Dq exp −
dτ
1 2 1
2 2
mq̇ + mω q − J(τ )q(τ ) .
2
2
(3.8)
Per calcolare esplicitamente la 3.8 possiamo procedere come per l’oscillatore armonico senza sorgente.
Z
1
0
KE [J] = C exp
dτ dτ 0 J(τ )DE (τ, τ 0 )J(τ 0 ).
2
DE è detto il propagatore del sistema e nel nostro caso vale
A−1 = DE (τ, τ 0 ) =
1 −w|τ −τ 0 |
e
2ω
A questo punto definisco W [J] in modo tale che K = eW . Nell’espansione
di W appaiono solo i grafi connessi 3 .
Inoltre abbiamo che per τ grande KE dipende solo dallo stato fondamentale
lim K(0, −τ /2; 0, τ /2) ≈ e−E0 τ |ψ0 (0)|2
(3.9)
τ →∞
Se siamo interessati allo spostamento che la perturbazione provoca allo
stato fondamentale basta considerare solo i grafi connessi.
3
Per vedere questo basta sviluppare in serie l’esponenziale e notare che ogni grafo si
può scrivere come prodotto di grafi connessi
3.2. L’OSCILLATORE ARMONICO PERTURBATO
19
Figura 3.2: I grafi pentavalenti con due vertici
Come esempio consideriamo una perturbazione VI = λq 5 .
Siamo iteressati alla correzione di ordine più basso allo stato fondamentale. Per trovarla dobbiamo considerare i grafi pentavalenti con due vertici
(vedi figura 3.2).
Ora calcoliamo la molteciplità 4 dei grafi. Il grafo A ha molteciplità 5!/2!:
possiamo connettere gli spigoli i, j, k, l, m in 5! modi diversi agli spigoli
i0 , j 0 , k 0 , l0 , m0 , poi bisogna dividere per 2! perchè i due vertici sono equivalenti. Il valore del grafo A è (per τ1 , τ2 grandi):
Z
Z
Z
Z
1
1 2
5
dτ1 dτ2 DE (τ1 , τ2 ) =
dτ1 dτ2 e−5ω|τ1 −τ2 | =
T
5
(2ω)
(2ω)5 5ω
Per calcolare l’integrale è stato fatto il cambio di variabile t = τ1 − τ2 e
2
T = τ1 +τ
2 .
Il grafo B ha molteciplità 5·5·3·3
2! ; possiamo scegliere in 5 · 5 modi la
coppia centrale.
A
sinistra
rimangono
4 indici da accoppiare; si possono
4
trovare 2 coppie, poi dobbiamo dividere per due perchè partizioni che si
ottengono scambiando il ”fiocco” sopra con quello sotto sono equivalenti
(le relazioni di incidenza non cambiano). Un discorso analogo vale per il
vertice di destra. Se poi dividiamo per 2! (i due vertici sono equivalenti),
otteniamo il risultato cercato. Il valore del gafo in questo caso è
Z
Z
1 2
2
dτ1 dτ2 DE (τ1 , τ2 ) DE
(τ , τ ) D2 (τ , τ ) =
T
| {z1 1} | E {z2 2} (2ω)5 ω
=1
Il grafo C ha molteplicità
1
2!
×
5
3
×
=1
5
3
× 3! = 300 e valore
La somma dei vari grafi (cioè il coefficiente di λ2 ) vale
Perciò l’espressione per il propagatore approssimato è
1
1
K = (ω/π) 2 (2 sinh ωT )− 2 e
1
2
T
(2ω)5 3ω
449
T
32ω 6
449λ2 T
32ω 6
4
La molteciplità di un grafo è il numero di partizioni diverse che rappresenta, cioè il
numero di modi diversi di costruire il grafo a meno dei suoi automorfismi (le applicazioni
che mandano vertici in vertici, spigoli in spigoli e preservano le relazioni di incidenza)
20
CAPITOLO 3. SVILUPPI PERTURBATIVI
Per trovare la correzione all’energia dello stato fondamentale basta fare
il limite per T → ∞
2
− ω/2− 449λ6 T
K → (ω/π)e
32ω
⇒ E0 ≈
ω 449λ2
−
2
32ω 6
Lo stesso risultato che si può trovare con la meccanica quantistica tradizionale
attraverso conti più gravosi.
Capitolo 4
Topologia e meccanica
quantistica
4.1
La particella in moto circolare
Una interessante domanda che ci si può porre è il ruolo che gioca la topologia dello spazio in meccanica quantistica; un sistema vincolato in uno spazio
che non sia Rn è influenzato dai vincoli imposti?
Il sistema più semplice che possiamo considerare è quello di un sistema
con un grado di libertà costretto a muoversi su una circonferenza. Può essere pensato come una particella su un anello o un elettrone in un reticolo
periodico infinito con condizioni al bordo periodiche.
In ogni caso prendiamo come coordinata l’angolo ϕ con ϕ = 0 e ϕ = 2π
identificati. La Lagrangiana del problema è L = 12 I ϕ̇2
Un cammino continuo in qesto spazio è una funzione continua ϕ(t), ancora con l’identificazione di 0 e 2π. L’insieme di questi cammini possono
essere divisi in funzione del loro indice di avvolgimento 1 . Cammini con lo
stesso indice di avvolgimento e gli stessi estrmi possono essere deformati
in modo continuo nello stesso cammino.
Il propagatore del nostro sistema diventa:
0
K(q , T ; q, 0) =
Z
iS[q(t)]
Dq(t)e
=
+∞ Z
X
n=−∞
Dqn (t)eiS[q(t)] =
+∞
X
Kn (4.1)
n=−∞
Dove Dqn (t) è l’integrale fatto sui cammini con indice di avvolgimento n.
1
Il numero di volte che un cammino gira attorno a un particolare punto in senso
antiorario meno il numero di volte che ci gira in senso orario
21
22
CAPITOLO 4. TOPOLOGIA E MECCANICA QUANTISTICA
Se assumiamo 2 che i Kn soddisfino singolarmente l’equazione
di Schrödinger
P
otteniamo che la forma più generare del propagatore è n An Kn .
Gli An non sono arbitrari ma devono essere della forma An = einδ con
δ ∈ R. Per vedere questo facciamo variare q 0 di 2π, Kn diventa Kn−1 mentre K non cambia (perchè non ci sono cambiamenti fisici al sistema), cioè
può essere moltiplicato solo per un fattore di fase. Se chiamiamo eiδ questo
fattore di fase otteniamo An+1 = eiδ An , se si fissa A0 = 1 si ottiene il risultato che volevamo dimostrare.
Per calcolare esplicitamente il propagatore consideriamo la mappa
p : R → S1
p(x) = x −
hxi
2π
2π
(4.2)
x
x
si intende la parte intera di 2π
Dove con 2π
.
p è localmente invertibile (bisogna solo fare attenzione che un intorno di
zero viene mappato nei multipli di 2π). Dato un cammino continuo ϕ(t)
su S 1 , con ϕ(0) = ϕ0 e ϕ(1) = ϕ00 , se una preimmagine di ϕ0 è stata scelta il
cammino può essere retratto a R.
É chiaro che cammini con gli stessi estremi e con la stessa scelta di p−1 (ϕ0 )
possono terminare con diverse preimmagini di ϕ00 . La preimmagine di
ϕ00 è determinata dall’indice di avvolgimento del cammino; infatti se n è
l’indice di avvolgimento di un cammino, questo termina a p−1 (ϕ00 ) + 2πn
dove p−1 (ϕ00 ) è la preimmagine di ϕ00 più vicino alla preimmagine scelta
per ϕ0 . Utilizzando la mappa p (che è sufficientemente regolare) possiamo
trasportare la Lagrangiana da S 1 a R, dove è quella di una particella libera.
Kn ha dunque la forma seguente
0
Kn (q , T ; q, 0) =
I
2πiT
1/2
iI
exp
(Q − 2nπ)2
2T
(4.3)
Dove Q = q 0 − q. Per esprimire il propagatore totale conviene ricordare la
definizione della funzione theta di Jacobi:
∞
X
θ3 (z, t) =
exp(iπtn2 + i2nz)
n=−∞
É una funzione analitica per =(z) > 0 e quasiperiodica 3 .
Utilizzando la funzione θ il propagatore assume la seguente forma
K=
2
I
2πiT
1/2
2
e(iIQ /2T ) θ3
πQI
δ 2πI
− ,
T
2 T
Questa assunzione sarà giustificata nell’appendice
Una funzione si dice quasiperiodica se soddisfa l’equazione funzionale
f (z + ω) = eaz+b f (z)
3
(4.4)
4.2. L’EFFETTO DI AHARONOV-BOHM
23
É interessante paragonare il propagatore 4.4 con il risultato che si raggiunge con la meccanica quantistica tradizionale. L’equazione di Schrödinger
per la particella sull’anello è
−
1 ∂2ψ
∂ψ
=i
2
2I ∂ϕ
∂t
(4.5)
Le soluzioni di questa equzione hanno la forma
1
ψm (ϕ, t) = √ eimϕ+iδϕ/2π e−Em t
2π
Em
1
=
2I
δ
m+
2π
Dove delta è il cambiamento di fase di un vettore sotto una rotazione di
2π (ψ(2π) = eiδ ψ(0)). Possiamo scrivere la fonzione di Green come somma
sgli stati stazionari:
X
∗
ψm (ϕ0 )ψm
(ϕ)e−1Em t
(4.6)
G(ϕ0 , t; ϕ, 0) =
m
Che ha la forma della funzione theta di Jacobi.
Per verificare l’uguagliaza delle 4.4 e 4.6 basta utilizzare una nota identità
della funzione theta4 :
z 1
−1/2 z 2 /iπt
θ3 (z, t) = (−it)
e
θ3
,−
t
t
4.2
L’effetto di Aharonov-Bohm
Un esempio fisico in cui la topologia non banale dello spazio porta a dei
risultati sorprendenti consta nell’effetto di Aharonov-Bohm magnetico.
Consideriamo la classica esperienza dell’interferenza di un fascio di elettroni con una doppia fenditura. La funzione d’onda ψ è approssimabile
nella forma ψ = ψ1 + ψ2 . Dove ψ1 e ψ2 sono le onde corrispondenti al
passaggio nella fenditura superiore o inferiore. La differenza di cammino
ottico provoca uno sfasamento relativo
∆φ =
2π
∆l
λ
∆l =
2xd
L
(4.7)
dando luogo alle note frange di interferenza nella misura di |ψ|2 = |ψ1 +
ψ2 |2 . L è la distanza tra le fenditure e lo schermo, d la distanza delle due
fenditure e x la distanza dal centro dello schermo di rilevazione.
4
Questa è l’identità fondamentale della funzione θ e segue direttamente dalla formula
di sommazione di Poisson
24
CAPITOLO 4. TOPOLOGIA E MECCANICA QUANTISTICA
Figura 4.1: Schematizzazione di un apparato per la verifica dell’effetto di
Aharonov-Bohm
Consideriamo ora l’identica situazione con l’aggiunta di un solenoide
(flusso magnetico φ, infinitamente lungo ed impenetrabile posto tra le fenditure e lo schermo di rilevazione.
Il campo magnetico all’esterno del solenoide è nullo e classicamente la
forza di Lorentz applicata a una particella carica (nl nostro caso un elettrone) è nulla.
Possiamo scegliere la Gauge del campo magnetico in modo tale ce il potenziale vettore è della forma Ar = 0, Aθ = Φ/2πr. L’Hamiltoniana in presenza del potenziale vettore è data da
H=
e l’azione è data da
1 q ~ 2
p~ − A
2m
c
Z
S=
dt
m ˙2 e ˙ ~
~x + ~x · A
2
c
(4.8)
(4.9)
Perciò, quando consideriamo la quantizzazione attraverso il Path Integral, appare un fattore di fase dovuto al potenziale vettore presente nell’azione,
Z
Z xf in
q˙ ~
~ = exp iδ(θ0 − θ + 2πnω )
exp i dt ~x · A = exp iq/c
d~x · A
c
xin
dove nω è l’indice di avvolgimento del cammino e δ = qΦ/2πc. Questo
fatore dipnde soltanto dall’angolo azimutale θ e da nω .
4.2. L’EFFETTO DI AHARONOV-BOHM
25
Il propagatore può essere calcolato in coordinate sferiche 5
KAB (r, r’; t) =
X
exp iδ(θ − θ0 + 2πn) Kn (r, r’; t)
n
Dove Kn è il propagatore della particella libera che ha fatto n giri.
Nel limite di alte energie possiamo possiamo utilizzare una stima semiclassica. Nel limite classico solo i cammini classicici hanno un contributo non
nullo (i due cammini rappresentati in figura 4.1). A causa del fattore di fase
dovuto al potenziale vettore lo sfasamento relativo 4.7 diventa
∆φ = ∆φ|Φ=0 +
e
Φ
~c
δx =
eλLΦ
4πc~d
Notiamo che al variare del flusso del campo magnetico si spostano le frange
di interferenza, dando luogo ad un effetto puramente quantstico. L’effetto
di Aharonov-Bohm evidenzia come le proprietà topologiche dello spazio
possano influenzare il comportamento del sistema.
5
vedi ad esempio [4]
26
CAPITOLO 4. TOPOLOGIA E MECCANICA QUANTISTICA
Capitolo 5
Gli istantoni
Esistono molti sistemi fisici che non possono essere trattati in modo esauriente utilizzando il metodo perturbativo.
L’esempio più semplice si ha per una particella in moto in un poteziale
unidimensionale. Il sistema può essere descritto dalla Lagrangiana
1
L = ẋ2 − V (x)
2
Dove V (x) è una funzione la cui serie di Taylor comincia con termini di
ordine x2 .
L’ampiezza di trasmissione obbedisce alla WKB formula,
Z
1
1 x2
2
|T (E)| = exp −
dx[2(V − E)] [1 + O(~)]
(5.1)
~ x1
Questa è un’approssimazione semiclassica. La penetrazione di bariera
non è però vista a nessun ordine della teoria delle perturbazioni, perche la
5.1 va a zero più rapidamente di ogni potenza di ~.
I problemi di tunneling possono essere anche risolti utilizzando il metodo
degli istantoni che può essere poi generalizzato a problemi di teoria dei
campi e QCD (il fenomeno del confinamento del colore è stato spiegato
con gli istantoni).
Figura 5.1: Barriera di potenziale
27
28
CAPITOLO 5. GLI ISTANTONI
Figura 5.2: Doppia buca di potenziale
Consideriamo una particella in un potenziale a doppia buca (vedi figura
5a). Chiamo V 00 (±a) con ω 2 .
Vogliamo calcolare
ha| e−HT /~ |ai = h−a| e−HT /~ |−ai
e
ha| e−HT /~ |−ai = h−a| e−HT /~ |ai
Vorremmo utilizzare una stima semiclassica (danno un contributo rilevante
solo i cammini classici con le condizioni al bordo opportune). Le uniche
soluzioni classiche sono qelle per cui la particella rimane nella buca (il
fenomene di tunnel è puramente quantistico). Se utilizziamo la formulazione euclidea, il sistema può essere visto come una particella in moto in
un potenziale −V (q) (vedi figura 5 b). In qesto caso ci sono altri cammini
classici oltre a quello banale: una particella può andare classicamente da
−a a +a. Il cammino che parte da −a è chiamato istantone, mentre quello che parte da +a anti-istantone. L’istantone parte da −a al tempo −T /2
e arriva a destra al tempo +T /2. Consideriamo le soluzioni classiche per
cui T tende ad infinito. In questo caso abbiamo a che fare con soluzioni
1
2
dell’equazione del moto con E nulla; cioè dx
dt = (2V ) o equivalentemente
Z x
1
t = t1 +
dx0 (2V )− 2
(5.2)
0
dove t1 è una costante di integrazione (il tempo per cui x è zero). Questa
soluzione è chiamata istantone di centro t1 .
É facile derivare un’espressione per S0 , l’azione di un istantone (o un
anti-istantone)
Z
Z a
1
1
2
S0 = dt[ (dx/dt) + V ] =
dx(2V ) 2
(5.3)
2
−a
Per tempi grandi, x si avviacina ad a e possiamo approssimare l’equazione
del moto con
ẋ = ω(a − x)
(5.4)
29
Perciò per grandi t (a − x) ∝ e−ωt ; gli istantoni sono in un certo senso
oggetti ben localizzati, con un’ampiezza dell’ordine di 1/ω.
Questo è motlto importante, perchè significa che l’istantone e l’anti-istantone
non sono le uniche soluzioni approssimate dell’equazione del moto; ci
sono anche soluzioni consistenti in stringhe di istantoni e anti-istantoni.
Per valutare l’interale funzionale dobbiamo sommare su tutte queste configurazioni, con n oggetti (istantone o anti-istantone) centrati a t1 , · · · tn
dove
T /2 > t1 > t2 > · · · > tn > −T /2
Per n oggetti molto separati, S è nS0 dove S0 è l’azione di un istantone.
Se siamo in un punto (nella scala temporale) lontano da un istantone o un
anti-istantone, V 00 è uguale a ω e si ottiene lo stesso risultato che per una
1
ω 2 −ωT /2
singola buca. Dove l’elemento di matrice è proporzionle a π~
e
.
Il piccolo intervallo che contiene l’istantone e l’anti-istantone corregge questa formula. Cosı̀ otteniamo
ω 1
2 −ωT /2
e
Kn
π~
dove K è definito in modo tale da dare la giusta risposta per un istantone.
Dobbiamo integrare su tutte le posizioni dei centri:
Z tn−1
Z T /2
Z t1
dt1
dt2 · · ·
dtn = T n /n!
−T /2
−T /2
−T /2
non siamo liberi di ditribuire istantoni e anti-istantoni arbitrariamente. Se
partiamo da −a il primo oggetto che incontriamo deve essere un istantone,
quello dopo un anti-istantone ecc. Inoltre se vogliamo tornare ad −a n
deve essere pari.
Perciò
ω 1
X KeS0 /~ T n
2 −ωT /2
−HT /~
h−a| e
|−ai =
e
[1 + O(~)]
(5.5)
π~
n!
n pari
mentre h−a| e−HT /~ |ai è dato dalla stessa espressione, sommata però
su gli n dispari. Queste somme possono essere calcolate esplicitamente 1 :
ω 1
h
i
2 −ωT /2
−HT /~
−S0 /~
−S0 /~
h±a| e
|−ai =
e
exp Ke
T ∓ exp −Ke
T
π~
(5.6)
Gli autostati del sistema con energia più bassa sono perciò
1
E± = ~ω ± ~Ke−S0 /~
2
1
Per una dimostrazione che questo risultato è equivalente a quello che si ottiene risolvendo l’equazione di Schrödinger si veda [7] nella seconda appendice del capitolo
7
30
CAPITOLO 5. GLI ISTANTONI
Chiamiamo questi due autostati |+i e |−i.
Gli autostati sono la combinazione pari e dispari dei due oscillatori armonici centrati sul fondo delle due buche; la degenerazione dei due autostati è
rotta solo dalla penetrazione della bariera (e infatti la differenza delle due
energie è proporzionale al fattore di penetrazione e−S0 /~ ).
Per calcolare K 2 dobbiamo studiare gli autovalori dell’equazione
2
− ddtx2n + V 00 (x̄)xn = λn xn dove x̄ è un singolo istantone. Si ottiene che il
contributo di un istantone all’elemento di matrice è:
1
1
h±a| e−HT /~ |−aiun istant. = N T (S0 /2π~) 2 e−S0 /~ (det0 [−∂t2 + V 00 (x̄)])− 2
(5.7)
Comparando questa con l’eq. 5.5 si trova
1
det(−∂t2 + ω 2 ) 2
K = (S0 /2π~) 0
det (−∂ 2 + V 00 (x̄)) 1
2
t
Potenziale periodico
Consideriamo ora un potenziale periodico, come quello presentato in figura 5.3. Se si ignora la penetrazione di barriera, gli autostati sono infinitamente degeneri e ciascuno è sul fondo di una buca. La penetrazione di
barrierea cambia questo singolo autostato in una banda continua di autostati; i veri autostati sono quelli delle traslazioni unitarie, le onde di Bloch.
Vediamo come questo risultato può essere ricavato con il metodo degli istantoni.
Come si può vedere dalla figura gli istantni sono molto simili al problema
precedente. L’unica novità è che un istantone puo partire da un qualunque
punto x = j (con j intero) e arrivare a x = j + 1. Non c’è più l’obbligo
che un istantone e anti-istantone debbano alternarsi; anche se un istantone
deve cominciare dove è arrivato il precedente. Il numero di istantoni meno
il numero di anti-istantoni deve essere uguale al cambiamento in x tra il
punto iniziale e finale.
Si ottiene
∞ X
∞
ω 1
X
1
2 −ωT /2
e
hj+ | e
|j− i =
(Ke−S0 /~ T )n+n̄ δn−n̄−j+ +j−
n!n̄!
π~
n=0 n̄=0
(5.8)
dove n è il numero degli istantoni e n̄ quello degli anti-istantoni.
−Ht/~
2
É lo stesso metodo usato per risolvere l’oscillatore amonico
31
Figura 5.3: Potenziale periodico
Se usiamo la nota identità
Z
δa−b =
2π
dθeiθ(a−b) /2π
0
la doppia sommatoria diventa due serie esponenziali indipendenti:
Z 2π
ω 1
2 −ωT /2
hj+ | e
|j− i =
e
dθei(j− −j+ )θ /2πexp[2KT cos θe−S0 /~ ]
π~
0
(5.9)
Cosı̀ abbiamo trovato un continuo di autostati dell’energia indicizzati da θ
con
1
E(θ) = ~ω + 2~K cos θe−S0 /~ .
2
Inoltre
ω 1
1
2
hθ| ji =
(2π)− 2 eijθ
π~
Che è la risposta corretta.
−Ht/~
32
CAPITOLO 5. GLI ISTANTONI
Bibliografia
[1] L. S. Schulman, Techniques and Applications of Path Integration, WileyInterscience Monographs and Texts in Physics and Astronomy, New
York, 1981.
[2] Richard P. Feynman and Albert R. Hibbs, Quantum Mechanics and Path
Integrals (McGraw-Hill, New York, 1965).
[3] J. Zinn-Justin. Quantum Field Theory and Critical Phenonema . Oxford
1992.
[4] G. Morandi e E.menossi, Path-Integrals in multiply connected spaces and
the Aharonov-Bohm effect, Eur. J. Phys. 5 (1984) 49-58
[5] M.G.G. Laidlaw and C.M. Dewitt, Feynman functional integrals for
systems of indistinguishable particles, Phys. Rev., t. D 3, 1971, p. 1375-1377.
[6] A I Vainshtein, V I Zakharov, V A Novikov, M A Shifman, ABC of
instantons, SOV PHYS USPEKHI, 1982, 25 (4), 195-215
[7] S. Coleman,Aspect of Symmetry, Cambridge U. P.
33



![[20120717] G.Giuni - La particella di Dio](http://s1.studylibit.com/store/data/007496773_1-f092519b9bc101b4085a20f32004c93f-300x300.png)