Le proprietà elettriche dei
semiconduttori.
dott.ssa Daniela Cavalcoli
[email protected]
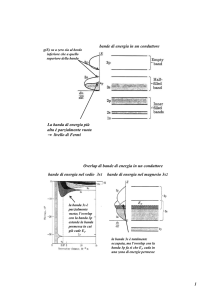
Diagramma a bande: semiconduttore non drogato
T>0
Banda di conduzione
(parzialmente piena)
EC
EF
EV
Banda di valenza
(parzialmente vuota)
A T = 0, la banda di valenza è piena di elettroni e la banda di
conduzione vuota →conducibilità
conducibilità zero.
zero
L’energia di Fermi EF è a metà di un gap piccolo (<1 eV) tra la banda di
conduzione e la banda di valenza.
A T > 0, gli elettroni vengono eccitati termicamente dalla banda di
valenza alla banda di conduzione, →conducibilità
conducibilità misurabile.
misurabile
2
D Cavalcoli
energy gap
bande di energia in un
semiconduttore
EF
Bande e conduzione elettrica
Ruolo delle bande nella conduzione elettrica
4
nei metalli
nei semiconduttori
D Cavalcoli
semiconduttori
Caratteristiche a 0K:
- banda di valenza completamente occupata
- banda di conduzione completamente vuota
-piccolo gap di energie proibite
Ec
Eg= 1,1 eV (Si); 0,7 eV (Ge); 1,4 eV (GaAs)
a T>0K:
- un elettrone può essere eccitato dalla banda di
valenza a quella di conduzione
- ogni elettrone che passa in banda di conduzione
lascia un posto vuoto (buca) in banda di valenza
- anche la buca in banda di valenza è “mobile”,
perché può essere occupata da un elettrone che
lascia a sua volta una buca e così via
- sotto l’azione di un campo elettrico esterno il
moto di deriva avviene sia in banda di conduzione
che in banda di valenza
- l’elettrone in banda di valenza è in una zona “di
massa efficace negativa” e il suo moto può essere
equiparato a quello di una particella con massa
positiva e carica elettrica positiva
Ega
p
Ev
buca
Semiconduttori-Diagramma a bande
Si Ge,
Reticolo del diamante
6
D Cavalcoli
GaAs,
Reticolo zincoblenda
Semiconduttori-diagramma a bande
I diagrammi a bande sono la chiave per conoscere le proprietà elettriche e
ottiche dei solidi
Questi diagrammi mostrano la relazione tra energia elettronica e momento per le
direzioni principali del cristallo definite in termini del reticolo reciproco
(trasformata di Fourier del reticolo del cristallo nello spazio reale)
E vs (h/2π)k oppure E vs k
Metodi di calcolo di strutture a bande
Tight banding method→ dagli orbitali atomici
→energie elettroniche nel solido
Calcoli di strutture a bande vicino al gap
Prima zona di Brilluin di un reticolo cubico a facce
centrate
I vari simboli denotano direzioni di elevata simmetria
nel cristallo
7
D Cavalcoli
Diagramma a bande del Si
Derivata da
orbitali p
Forbidden gap
Derivata da
orbitali s
Banda di valenza
in Si vicino al
punto
8
ᴦ (k=0)
D Cavalcoli
Interazione
spinorbita→rompe
la simmetria
triplice della
banda al punto
ᴦ
Il Si è un semiconduttore a gap indiretto
Per piccole variazioni del vettore d’onda dal
punto ᴦ le bande possono essere considerate
paraboliche
9
D Cavalcoli
Si Diagramma a bande
Electrons:
The surfaces of equal energy are ellipsoids.
ml= 0.98mo
mt= 0.19mo
Effective mass of density of
states
mc = 0.36mo
There are 6 equivalent valleys in the conduction band.
mcc= 0.26mo
Holes:
Heavy
mh = 0.49mo
Light
mlp = 0.16mo
Split-off band
mso = 0.24mo
Effective mass of density of
states
mv = 0.81mo
http://www.ioffe.ru/SVA/NSM/Semicond/Si/index.html
10
D Cavalcoli
Ge
Electrons:
The surfaces of equal energy are ellipsoids
ml = 1.59mo
mt = 0.0815mo
Effective mass of density of states
mc=(9mlmt2)1/3
mc=0.22mo
Effective mass of
conductivity
mcc=0.12mo
Holes:
11
Heavy
mh = 0.33mo
Light
mlp = 0.043mo
Split-off band
mso = 0.084mo
Effective mass of density of
states
mv = 0.34mo
D Cavalcoli
GaAs diagramma a bande
Il GaAs è un
semiconduttore a gap
diretto
Con m* = 0.067 m0
Gap diretto e gap indiretto
Grande influenza sulle proprietà ottiche
12
D Cavalcoli
Masse efficaci per banda di valenza e di
conduzione
Conductivity mass usata nel
calcolo delle proprietà
elettriche
13
D Cavalcoli
conducibilità elettrica nei semiconduttori
heavy
hole
light
hole
masse efficaci
molto piccole
due contributi alla conducibilità:
σ = neµ n+ peµ p
contributo degli elettroni in
banda di conduzione
contributo delle buche in
banda di valenza
Concentrazione dei portatori
15
D Cavalcoli
semiconduttore intrinseco: n=p
conducibilità elettrica nei
semiconduttori
Calcolo di n e di p:
∞
∞
∫
∫
8π 2me3
( E − Ec )dE
n = g ( E ) f F ( E , T )dE =
3
( E − E F ) / k BT
h
e
+1
Ec
Ec
∞
∞
∫
∫
3
m
8π 2me3 E F / k BT
8
π
2
− E / k BT
e
3 / 2 E F / k BT
−x
=
e
e
(
E
−
E
)
dE
=
(
k
T
)
e
e
x dx
c
B
3
3
h
h
E
0
c
me k B T
n = 2
2πh 2
3/ 2
e − ( Ec − E F ) / k BT
legge dell’azione di massa
m k T
p = 2 h B
2πh 2
me m h k B T
np = 4
2πh 2
3
3/ 2
e − ( E F − Ev ) / k BT
− E gap / k B T
e
Calcolo del livello di Fermi per il
semiconduttore intrinseco
Livello di
Fermi
- n i = pi
- si assume me≈ mh=m*
3/2
m *k B T
n = 2
2π h 2
m k T
n = 2 e B
2πh 2
3/ 2
e
Egap
EF
− E gap / 2 k B T
e − ( Ec − E F ) / k BT
dal rapporto:
Ec-EF = Egap/2
EF = Ec - Egap/2
Stima di ni a 300K:
3/ 2
6
−2
2 3 / 2
m*c2kBT
−2
e− Egap / 2kBT ≈ 2 0,2 ⋅ 0,5 ⋅ 10 ⋅ 3 ⋅10 (eV ) e−1.1 / 2⋅3⋅10
ni = 2
2π (hc)2
6 ⋅ (2 ⋅ 10−7 eVm)2
(
)
16 −2 3 / 2 −18
≈ 10 m
e
≈ 1016 m−3
- da confrontarsi con ≈ 1029m-3 per i conduttori
- inoltre dipendenza esponenziale dalla temperatura
Calcolo del livello di Fermi per un
semiconduttore intrinseco
Da n=p
18
D Cavalcoli
“drogaggio”
donatore
EF
livello del
donatore
drogaggio tipo “n” con un
atomo pentavalente
(fosforo)
accettore
livello
dell’accettore
EF
drogaggio tipo “p”
con un atomo
trivalente (Al)
Drogaggio
Energia di ionizzazione di un atomo di idrogeno
Per l’elettrone poco legato associato all’
atomo di donore
≈25 meV
20
D Cavalcoli
Concentrazione dei portatori vs T
Neutralità di carica
21
D Cavalcoli
conducibilità elettrica in
semiconduttori drogati
EF
“n”
“p”
livello del
donatore
livello
dell’accettore
EF
con un drogaggio di tipo “n”, la conducibilità è
dovuta praticamente solo alla densità nd dei
donatori (portatori di maggioranza)
σ n = nd eµ e
con un drogaggio di tipo “p”, la conducibilità è
dovuta praticamente solo alla densità na degli
accettori (portatori di minoranza)
σ p = na eµ h
resistenza elettrica in semiconduttori
debolmente drogati
zona “estrinseca”: tutti i
portatori di
maggioranza sono in
banda di conduzione, la
resistenza elettrica
cresce linearmente con
T perché cala la mobilità
zona “intrinseca”: i
portatori “intriseci”
cominciano a passare
con crescente
probabilità in banda di
conduzione, la
resistenza elettrica
diminuisce
esponenzialmente con T
perché cresce la densità
n di portatori
Riassumendo un semiconduttore ha:
A T= 0K:
-banda di valenza completamente occupata
- banda di conduzione completamente vuota
- piccolo gap di energie proibite Eg= 1,1 eV (Si); 0,7 eV (Ge); 1,4 eV (GaAs)
A T>0K:
- un elettrone può essere eccitato dalla banda di valenza a quella di conduzione
- ogni elettrone che passa in banda di conduzione lascia un posto vuoto (buca) in
banda di valenza
- anche la buca in banda di valenza è “mobile”, perché può essere occupata da
un elettrone che lascia a sua volta una buca e così via
- sotto l’azione di un campo elettrico esterno il moto di deriva avviene sia in
banda di conduzione che in banda di valenza
due contributi alla conducibilità:
24
σ = neµ n+ peµ p
contributo degli elettroni
in banda di conduzione D Cavalcoli
contributo delle buche
in banda di valenza
Conduciblità,
semiconduttore drogato
(tipo n)
A basse T, in regime estrinseco
Nd >> ni ; n>>p, → n= Nd + ni ≈ Nd
n è indipendente da T, quindi σ = neμ = Nd eμ(T)
→ σ vs T come μ vs T (μ≈T-3/2)
A T maggiori, in regime intrinseco
gli elettroni “saltano” in banda di conduzione, Nd << ni,
n ≈ ni, σ=neμe+ peμh visto che μ indip da T σ vs T come ni, vs T, in
particolare ni≈T3/2 exp(-E g /2KT)
Un plot semilogaritmico di σ vs T fornisce una linea
retta di pendenza Eg(0)/2K
25
D Cavalcoli