capitolo 3. le derivate

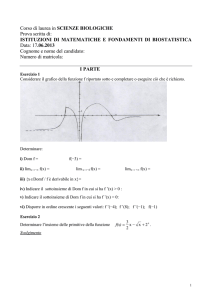
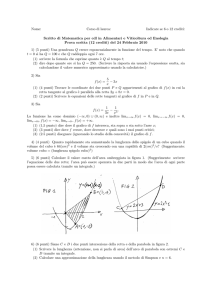
Capitolo 3
Le Derivate
L’Analisi ed il suo calcolo rappresentano la matematica del cambiamento. Il
potere dell’analisi deriva dalla sua abilità nel descrivere e predire il comportamento di quantità che cambiano. La caduta delle mele, il movimento di razzi
spaziali, la crescita di popolazioni, il decadimento radioattivo, la crescita dei
prezzi al consumo possono essere modellati con i metodi dell’analisi.
Tra questi, particolare rilevanza è assunta dall’operazione di derivazione
delle funzioni. Nei capitoli seguenti la maggior parte dello sforzo sarà concentrato su come definire formalmente l’operazione di derivazione e su come
calcolarla simbolicamente. Nella costruzione di questo processo ci troveremo di
fronte a varie sottigliezze e a vari problemi, ma l’idea base che sta sotto a tutto
il processo è semplice:
Data una funzione f , la funzione derivata, che indicheremo con f 0 indica
il tasso di variazione di f .
Questo principio, interpretato correttamente, sta dietro a tutti i nostri
calcoli e applicazioni delle derivate.
L’idea di derivata non appartiene ad un singolo individuo. Idee e metodi
correlati appaiono attraverso tutta la storia della matematica per almeno 2000
anni. Lo sviluppo moderno dell’idea e calcolo della derivata avviene tra il 17esimo e 18-esimo secolo partendo da Pierre de Fermat (1601-1655, Francia),
attraverso Isaac Newton (1642-1727, Inghilterra) e Gottfried Leibnitz (16461716, Germania) - generalmente considerati i cofondatori del calcolo moderno
- per arrivare a Leonhard Euler (1707-1783, Svizzera) e Joseph-Louis Lagrange
(1783-1813, Francia). Lagrange, in particolare, partendo dalle idee di Euler sembra essere stato il primo ad usare la dizione “funzione derivata” ed ad adottare
il simbolo f 0 per indicarla.
Questo capitolo è dedicato allo sviluppo del concetto di derivata. La relazione tra f ed f 0 ne è il tema fondamentale; studieremo che cosa significa per
f 0 essere il tasso di cambiamento di f , che cosa ognuna ci dice dell’altra e in
special modo come sono correlati i grafici delle due funzioni. Finiremo con la
definizione formale e a seguire con le tecniche per il calcolo formale.
Uno dei problemi da capire è se tutte le funzioni ammettono derivata o
meno e qual’è il possibile comportamento della derivata. In questo capitolo,
comunque assumeremo sempre (a meno di esplicita negazione) che le funzioni
91
92
CAPITOLO 3. LE DERIVATE
f date ammettano funzione derivata f 0 , che sia f che f 0 abbiano un grafico
liscio, senza strappi. Più avanti, quando saremo in grado di sviluppare nuovi
linguaggi e nuove tecniche, studieremo, con maggior attenzione, tutto ciò che
può andare storto e non funzionare.
3.1
La Derivata come Variazione
Ogni funzione può essere usata per costruire, in un qualche modo, nuove funzioni. Per esempio, partendo da f (x) = sin x possiamo costruire nuove funzioni
a nostro piacimento. Le funzioni
sin (x + 0.1) − sin x
0.1
sono tutte “derivate” a partire da f ; le possibilità sono infinite.
Tra tutte le funzioni che uno può costruire a partire da una data funzione f
la funzione derivata f 0 è senza dubbio la più importante. Eccone una descrizione
informale.
g (x) = sin 2x , h (x) = sin (x + π/2) , e k (x) =
Definizione 49 (La derivata come variazione). Sia f una funzione. La nuova
funzione f 0 , chiamata la derivata di f è definita dalla regola
f 0 (x) = il tasso di variazione istantanea di f nel punto x.
3.1.1
Quantità, Variazioni ed Automobili: Un Primo Esempio
Il movimento di un’automobile ci fornisce l’ambientazione ideale per capire il
senso della definizione ed il rapporto esistente tra quantità e loro variazione ed
anche alcuna delle sottigliezze nascoste. Vediamo una situazione tipica, ridotta
all’essenziale:
A mezzogiorno del 1 ◦ Gennaio 1999 un’automobile parte da Firenze diretta verso sud. Per diverse ore l’automobile si muove, a varie
velocità ed in varie direzioni.
Per mettere questo scenario in un linguaggio funzionale, definiamo alcuni
simboli:
t
tempo trascorso, misurato in ore, assumendo t = 0 alla partenza
P (t) posizione al tempo t misurata in km a partire da Firenze Nord
V (t) velocità dell’auto verso sud, misurata in km/h
Ecco di seguito i grafici di posizione e velocità
Grafico di P (t)
Grafico di V (t)
3.1. LA DERIVATA COME VARIAZIONE
93
Molte sono le cose da osservare:
Punti di Riferimento. La scelta del tempo e del punto di riferimento è stata interamente arbitraria. Avremmo potuto scegliere come date di riferimento
il 1 ◦ giugno e come punto di partenza Bologna.
Posizione e velocità come funzione del tempo. Una volta specificati i
punti di riferimento e le unità di misura, P e V diventano funzioni del tempo t
: ad ogni istante di tempo l’auto ha una posizione ed una velocità ben definite
P (t) e V (t) . Per esempio le uguaglianze
P (2) = 80 , V (2) = 90
significano che alle 2 del pomeriggio l’auto si trova 80 km a sud di Firenze e
viaggia alla velocità di 90 km/h.
Quantità e cambiamento. E’ naturale pensare a P come la funzione
quantità e a V come la funzione di variazione associata. Per ogni istante t,
V (t) è indica il tasso di variazione istantanea di posizione al variare del tempo.
In simboli, V (t) = P 0 (t) , o semplicemente V = P 0 .
Valori positivi e negativi. Sia P che V assumono valori sia positivi che
negativi. L’affermazione
P (7) = −100 , V (7) = −70
significano che alle 7 di sera la macchina è 100 chilometri a nord di Firenze e
viaggia a 70 km/h. Ne consegue che quando P (t) > 0 l’auto è a sud di Firenze.
Quando V (t) > 0 l’auto si dirige verso sud.
Che cosa dice e che cosa non ci dice il tachimetro dell’auto. Il
tachimetro non ci dice la direzione nella quale viaggia l’auto. Ci dice però che
se segna un valore di 80 all’istante t = 4 allora V (4) = ±80. La lettura del
tachimetro è d’altra parte una lettura istantanea. Significa solo che se l’auto
mantiene la stessa velocità per un’ora, percorre 80 km.
Accelerazione. La velocità, così come la posizione, ha sua funzione di
variazione. Nel linguaggio fisico, la nuova funzione di variazione si chiama
accelerazione. Così come posizione e velocità, l’accelerazione varia con il tempo,
in simboli A (t) = V 0 (t) . Anche l’accelerazione, come la velocità, può essere
positiva o negativa. L’affermazione A (3) > 0 significa, per esempio che al
tempo t = 2 la velocità della macchina sta crescendo. In modo analogo A (4) < 0
implica che per t = 4 la velocità sta decrescendo
Velocità - Variazione o Quantità ? Abbiamo dapprima visto la velocità
come la funzione variazione della “quantità” posizione. Ora il nostro punto di
vista è cambiato. Quando consideriamo l’accelerazione, la velocità diventa la
quantità che varia. Ne consegue che ogni funzione può essere considerata come
il tasso di variazione di un’altra o come una quantità che varia da cui ricavare
il tasso di variazione, dipende dalla situazione. La nomenclatura è solo legata
alla visione che abbiamo del fenomeno.
Unità di velocità e di accelerazione. Ogni variazione, propriamente intesa, è la variazione di qualcosa rispetto ad altro. Le unità proprie per misurare
il tasso di variazione dipendono sia dalla quantità che si misura che dall’unità
di misura scelta per misurare le quantità.
94
CAPITOLO 3. LE DERIVATE
Nella situazione in esame, la velocità è il tasso di variazione dello spazio
(misurato in km) rispetto al tempo (misurato in h), così l’unità di velocità sono
i km/h. L’accelerazione misura il tasso di variazione di velocità col tempo,
quindi la sua unità di misura è il (km/h)/h=km/h 2 .
L’idea di quantità che varia e della misura della sua variazione
Funzione Variazione in Altri Contesti.
L’idea di misurare il tasso di variazione della grandezza (o quantità) di una
funzione è intuitivamente naturale quando applicata a grandezze fisiche come
posizione, velocità, ma l’idea ha senso anche in altri contesti. Se f (t) è la posizione al tempo t di un oggetto che si muove, allora f 0 (t) rappresenta la velocità
dell’oggetto al variare del tempo. Se f (t) rappresenta l’altezza di un pallone
aerostatico in funzione del tempo, allora f 0 (t) rappresenta la velocità di salita
dell’oggetto. Se f (t) rappresenta la quantità di denaro depositata in un conto
in banca, f 0 (t) rappresenta il tasso di variazione di flusso di denaro nel conto
stesso. Se f (x) misura la quantità di benzina consumata dopo aver percorso
x chilometri, allora f 0 (x) rappresenta la rapidità di consumo di carburante in
litri/km.
Anche se f è una funzione matematica, senza alcuna relazione a auto, palloni,
benzina e quant’altro, l’idea di misurarne la variazione è sensata e fruttuosa.
In questo caso f 0 misura quanto rapidamente l’uscita di f varia al variare dell’ingresso x. Indicato con y = f (x) si ha che f 0 (x) rappresenta la variazione,
nel punto x della quantità y. Per esempio, se f 0 (3) = 5 questo significa che se
x ≈ 3 una piccola variazione di x produce una variazione cinque volte maggiore
in f (x) .
La Derivata dal Punto di Vista Grafico:
Pendenza.
f0
come Funzione
Cosa significa la deriva graficamente? Come il grafico di f e di f 0 riflettono
la relazione quantità-variazione?
Pendenza è l’idea chiave che legano grafici e variazioni. Per definizione, la
pendenza è la quantità di variazione, cioè il rapporto tra due cambiamenti, ∆x
e ∆y. Specificamente, la pendenza del grafico della funzione f in ogni punto
(x, f (x)) è il tasso di variazione istantanea di f rispetto ad x. Riassumendo:
Definizione 50 (La derivata come funzione pendenza) Sia f una funzione. La
funzione derivata f 0 è data dalla regola
f 0 (x) = valore della pendenza del grafico di f in x.
Come la precedente, anche questa definizione di derivata necessita di chiarimenti e raffinamenti. Vediamo dapprima che cosa significa la definizione.
Cominciamo con il caso più semplice di funzioni lineari.
3.1. LA DERIVATA COME VARIAZIONE
95
Esempio 51 Sia f la funzione lineare f (x) = 3x + 1. Spiegare graficamente
ed in termini di variazione perché la derivata è la funzione costante f 0 (x) = 3.
Soluzione. Il grafico di f è una retta, così la sua pendenza, per ogni valore
del parametro x è 3. In simboli f 0 (x) = 3 per ogni x. Qui di seguito sono
tracciati i grafici di f e f 0
-4
-3
-2
8
8
6
6
4
4
2
2
-1 0
-2
1
2x
3
4
-4
-3
-2
-1
0
-2
-4
-4
-6
-6
-8
-8
Grafico di f (x) = 3x + 1
1
x2
3
4
Grafico di f 0 (x) = 3
Il fatto che f sia lineare di coefficiente angolare 3 significa che il grafico di f
cresce ovunque con un incremento di 3 unità di y per ogni unità di x.
¥
L’esempio illustra una proprietà generale
Per ogni funzione lineare f (x) = ax + b, la funzione derivata
è la funzione costante f 0 (x) = a
La Pendenza di un Grafico in un Punto: Rette Tangenti.
Per funzioni lineari la nozione di pendenza è semplice. Una retta ha una
sola pendenza e bastano due punti sul grafico per calcolarla. Che cosa accade,
come comportarsi quando il grafico di una funzione non è una retta ? Come
calcolare la pendenza in un punto ? In realtà vi è una domanda ancora a monte:
In generale, una curva ammette pendenza in un punto ?
Definire e trovare il valore della pendenza di una curva in un punto sono due
idee chiave (probabilmente le due idee chiave) dell’analisi. In questo paragrafo
cominceremo col dare un primo approccio grafico al problema, nel prossimo
ritorneremo sul problema studiandolo con maggiori dettagli.
La pendenza di una curva in un punto P può essere pensata come la pendenza della retta tangente in P .
Volendo ancora usare la strada, vista come una curva, e l’auto, potremmo dire
che la tangente in un certo punto P della strada è la retta indicata dai fari
anteriori.
Usando queste idee intuitive è possibile tracciare le rette tangenti ad un
grafico, in un punto, con ragionevole accuratezza e calcolare quindi la loro
pendenza.
Qui di seguito è riportato come esempio il grafico della funzione f (x) = x3 +
x2 − 6x
96
CAPITOLO 3. LE DERIVATE
Esempi di rette tangenti
Il segmento tangente più a sinistra, valutato per x = −1 appare essere
orizzontale; nella notazione delle funzioni f 0 (−1) ≈ 0. Una stima delle pendenze
delle altre due rette suggerisce che f 0 (1) ≈ −5 e f 0 (3) ≈ 15. (Controllare le
stime).
Relazione tra Funzioni e Funzioni Derivate.
Come sono collegate tra di loro f ed f 0 ? Che cosa di dice una funzione
dell’altra ? Queste questioni sono il fondamento dell’Analisi. Ci torneremo
sopra ripetutamente da tutti i punti di vista, grafico, numerico e simbolico. Nel
proseguo del paragrafo cominceremo questa discussione.
Il Pr incipio delle Corse : Il cavallo più veloce vince.
Ecco una affermazione ovvia:
Se due cavalli f e g partono insieme e g corre sempre più velocemente del cavallo f , allora il cavallo g è sempre in testa e vince
la gara.
Questo principio delle corse, riparafrasato appropriatamente è sorprendentemente utile: Il primo passo è reinterpretare l’affermazione in linguaggio
matematico.
Ecco un modo di farlo
Il principio delle Corse. Siano f e g due funzioni definite per tutti
i valori x dell’intervallo [a, b] e supponiamo che f (a) = g (a) . Se
f 0 (x) ≤ g 0 (x)
per tutti gli x ∈ [a, b] , allora
f (x) ≤ g (x)
per tutti gli x ∈ [a, b] .
Osservare con attenzione i vari punti della affermazione:
3.1. LA DERIVATA COME VARIAZIONE
97
Partenza equa. La richiesta che f (a) = g (a) implica che f e
g partono insieme per x = a.
Variazione nella crescita. L’affermazione che f 0 (x) ≤ g 0 (x)
significa che f “non cresce più rapidamente” di g per a ≤ x ≤ b.
Mai in testa. La conclusione significa che f “non sorpassa mai”
g per a ≤ x ≤ b.
Disuguaglianza stretta. Una versione più stringente del principio delle corse si ha quando si considera una disuguaglianza stretta:
Se f (a) = g (a) e f 0 (x) < g 0 (x) per a ≤ x ≤ b, allora f (x) < g (x)
per ogni x in [a, b] .
Esempio 52 Sia f una funzione tale che (i) f (0) = 0; (ii) f 0 (0) ≤ 10 se
x ≥ 0. Mostrare che f (1) ≤ 10.
Soluzione. Ragionando in modo informale, possiamo dire che la condizione
(ii) implica che la crescita della funzione non è maggiore alle 10 unità y per ogni
unità x. In modo equivalente si può dire che la pendenza del grafico non supera
mai 10. Quindi, quando la variabile x si sposta di una unità (da x = 0 a x = 1),
y non può salire più di 10 unità (da y = 0 a y = 10), ne consegue che f (1) ≤ 10.
Il principio delle corse descrive quanto detto in modo più formale. Per applicarlo
consideriamo la funzione lineare g = 10x (abbiamo scelto questa particolare g
perché ha pendenza costante 10, così g 0 (x) = 10 ed inoltre g (0) = f (0) = 0. A
questo punto si sono costruiti tutti gli elementi, perché g (0) = f (0) e f 0 (x) ≤
10 = g 0 (x) . Il principio delle corse garantisce che per tutti gli x ≥ 0 si ha
f (x) ≤ g (x) = 10x. Ponendo x = 1 si ottiene il risultato, f (1) ≤ g (1) = 10. ¥
Una Variante del Principio delle Corse.
Il principio delle corse - il cavallo più veloce è sempre in testa - può essere
riparafrasato in molte altre forme utili, cambiando leggermente le condizioni.
Nelle tre varianti che seguono, non assumeremo più che i cavalli f e g partano
insieme. Esprimeremo sempre il principio prima a parole, poi in formule.
Uguale Velocità, Uguale Distanza. A parole: se due cavalli
corrono alla stessa velocità nell’intervallo di tempo che va da a a b,
allora la distanza tra di loro rimane inalterata.
In simboli: Se f 0 (x) = g 0 (x) per a ≤ x ≤ b allora si ha che f (x) −
g (x) = C per qualche costante C e per tutti gli x ∈ [a, b] .
Maggior velocità, Maggior Distanza. A parole: Se il cavallo
f non corre più forte del cavallo g, allora il cavallo f non distanzia
il cavallo g più di quanto lo fosse al tempo iniziale a.
In simboli: Se f 0 (x) ≤ g 0 (x) per a ≤ x ≤ b allora
f (x) − f (a) ≤ g (x) − g (a)
per ogni x ∈ [a, b] .
(Notare che f (x) − f (a) e g (x) − g (a) rappresentano, rispettivamente, la distanza percorsa da f e da g nell’intervallo di tempo
che va da a ad x.
98
CAPITOLO 3. LE DERIVATE
Foto Finish. Se i due cavalli f e g arrivano insieme, allora il
cavallo più veloce non può essere stato davanti per tutto il tempo.
In simboli: Supponiamo che f 0 (x) ≤ g 0 (x) per a ≤ x ≤ b e che
f (b) = g (b) , allora:
f (x) ≥ g (x) per a ≤ x ≤ b .
Esempio 53 Supponiamo che f (0) = 3 e f 0 (x) ≤ 2 per tutti gli x. Cosa
possiamo dire di f (2) e di f (−4) ? Interpretare il risultato graficamente.
Soluzione. Applichiamo il principio delle corse con g (x) = 2x + 3. Abbiamo scelto questa g perché (i) f (0) = g (0) e (ii) f 0 (x) ≤ 2 = g 0 (x) . Per
stimare f (2) usiamo il principio delle corse nella sua formulazione standard,
nell’intervallo [0, 2] . Si ha che
f (0) = g (0) e f 0 (x) ≤ g 0 (x) =⇒ f (2) ≤ g (2) = 7 .
Per stimare f (−4) usiamo il principio, nella sua versione foto finish, nell’intervallo [−4, 0] . Esso dice che
f (0) = g (0) e f 0 (x) ≤ g 0 (x) =⇒ f (−4) ≥ g (−4) = −5 .
Tutto ciò può essere compreso graficamente. Ecco dei possibili grafici per f e g
10
8
6
4
2
0
-2
-4
-6
-8
-4
-3
-2
-1
x
0
1
2
3
Grafici di f e g
Come la figura mostra i grafici di f e di g si sovrappongono per x = 0 ed f non
cresce mai più rapidamente di g. Come conseguenza del principio delle corse,
il grafico di f giace sotto quello di g per x > 0 e sopra quello di g per x < 0.¥
Ancora sulle Derivate.
Molti fenomeni del mondo reale coinvolgono quantità e le loro variazioni; le
derivate sono proprio ciò che occorre per descrivere e predire il loro comportamento.
Terminiamo questo paragrafo con alcuni esempi di applicazione delle derivate.
Come detto sopra, rimandiamo il loro calcolo al paragrafo successivo.
Moto in Caduta Libera Senza Resistenza dell’Aria.
3.1. LA DERIVATA COME VARIAZIONE
99
Un oggetto in movimento è detto in caduta libera se l’unica forza a cui è
soggetto è la forza di gravità. Si assume che altre forze - resistenza dell’aria,
spinta del motore, etc. - non giochino alcun ruolo.
La gravità esercita la stessa accelerazione verso il basso su oggetti che cadono
indipendentemente dalla loro forma, massa, velocità iniziale o altre caratteristiche. Per oggetti nelle vicinanze della terra questa accelerazione può essere considerata essenzialmente costante. Si dice che Galileo Galilei (1564-16642) scoperse questa proprietà lanciando oggetti dalla torre pendente di Pisa e notando
che essi atterravano nello stesso istante.
[Si può davvero ignorare la resistenza dell’aria? Nella realtà la resistenza dell’aria
conta. I paracadutisti, per esempio devono ad essa la loro capacità di scendere lentamente dal cielo; le palle di cannone cadono a terra più velocemente delle piume. D’altra
parte, da un punto di vista fisico, la resistenza dell’aria è usualmente trascurabile quando si studia la caduta di oggetti piccoli e densi, che si muovono a bassa velocità, come
nel caso, ad esempio, di una moneta che cade sul pavimento. ]
Un oggetto che cade ha, ad ogni istante di tempo t un’altezza h (t) , una
velocità v (t) ed una accelerazione a (t) . Date le opportune unità di misura di
tempo l’altezza, la velocità e l’accelerazione sono funzioni del tempo legate tra
di loro dalle relazioni v = h0 ed a = v 0 .
La scoperta di Galileo che un oggetto in caduta libera ha un’accelerazione verso
il basso costante si traduce matematicamente dicendo che:
a (t) = −g , o in modo equivalente che v 0 (t) = −g
per qualche costante g. (Il segno negativo perché l’accelerazione è verso il
basso). Nel sistema MKS g vale circa 9.82 m/ sec2 .
Formule per velocità e distanza. Alla fine del 1600 Newton usò la
scoperta di Galileo per derivarne le sue leggi del moto. Il ragionamento di
Newton fu che se l’accelerazione (come nel caso della caduta libera) è costante
allora la velocità deve essere lineare.
Se supponiamo che all’istante iniziale di osservazione del fenomeno (t = 0)
l’oggetto avesse un’altezza h0 ed una velocità verticale positiva v0 , le leggi di
Newton ci dicono che
h (t) = h0 + vo t − 1/2 g t2 ; v (t) = v0 − g t .
Con queste formule possiamo rispondere a molte delle questioni legate al moto
in caduta libera.
Esempio 54 Può un giocatore di tennis lanciare una pallina ad un’altezza di
100 metri?
Soluzione. Come sappiamo, i campioni più forti riescono a battere ad una
velocità intorno ai 210 km/h che rappresentano circa 60 m/ sec . Supponendo
pure che riescano ad imprimere la stessa velocità lanciando verso l’alto e che
l’altezza dell’atleta sia di 1.80 m. si ha che le formule per velocità e posizione
come funzione del tempo sono:
h (t) = 1.80 + 60 t −
1
9.82 t2 ; v (t) = 60 − 9.82 t
2
100
CAPITOLO 3. LE DERIVATE
L’altezza massima si raggiunge quando la velocità si annulla (la pallina smette
di viaggiare verso l’alto per ricadere) e cioè per
v (t) = 60 − 9.82 t = 0 =⇒ t =
60
≈ 6. 11 sec
9.82
Per questo valore del tempo l’altezza è
h (6.11) = 1.80 + 60 · 6.11 −
1
· 9.82 · (6.11)2 = 185. 1
2
più alta dei 100 metri proposti. Di seguito sono riportati i grafici di h (t) e di
v (t) .
200
60
180
40
160
140
20
120
100
0
80
-20
60
40
-40
20
0
2
4
6t
8
10
12
Grafico di h (t)
-60
2
4
6t
8
10
12
Grafico di v (t)
Equazioni Differenziali.
Ogni equazione che coinvolga una funzione e le sue funzioni derivate è
chiamata equazione differenziale (ED). Le equazioni
f 0 (x) = 2 ; v (t) = −b + k v (t)2 ; f 0 (x) = f (x)
sono ED. Una soluzione di un’equazione differenziale è una funzione che con
le sue derivate soddisfa l’equazione (come abbiamo visto f (x) = 2x + 1 è una
soluzione della prima; vedremo più avanti le altre).
La maggior parte delle applicazioni più importanti dell’analisi - specialmente
le applicazioni di tipo fisico - coinvolgono la formalizzazione di problemi come
equazioni differenziali, la loro soluzione ed il loro uso.
Cadendo con la Resistenza dell’Aria.
E’ un dato fisico che quando un oggetto piccolo e denso cade a bassa velocità, la decelerazione dovuta alla resistenza dell’aria è (approssimativamente)
proporzionale al quadrato della velocità. Usando la notazione per le derivate si
ha questo ci dice che
v 0 (t) = a (t) = −g + k v (t)2
per qualche costante positiva k, dove g rappresenta sempre l’accelerazione di
gravità. Il valore numerico della costante k dipende da fattori fisici quali: forma
e peso dell’oggetto, densità dell’aria e così via. Per una pallina che cade, un
fattore k ≈ 0.007 è ragionevole.
3.1. LA DERIVATA COME VARIAZIONE
101
Figura 3.1: Effetto dell’aria sulla posizione
Figura 3.2: Effetto dell’aria sulla velocità
Esempio 55 Consideriamo una palla da tennis che cade, partendo da ferma,
da circa 200 m. Qual’è la differenza di velocità a terra nei due modelli proposti?
Soluzione. Senza la resistenza dell’aria la legge di Newton ci dice che
h (t)
= 200 − 12 9.82 t2
h0 (t) = v (t) = −9.82 t
v 0 (t) = a (t) = −9.82
Tenendo conto della resistenza dell’aria si ha che l’equazione per l’accelerazione diventa
v 0 (t) = −9.82 + 0.007 v (t)2
Risolvere questa ED simbolicamente non è facile, ma vogliamo mostrare i
grafici di velocità e posizione
Le due curve mostrano la differenza nei due casi. Con l’attrito dovuto all’aria
la palla arriva in fondo con una velocità di circa 38 m/ sec contro gli 80 m/ sec
che avrebbe in assenza d’aria, una velocità più che doppia della precedente.
102
CAPITOLO 3. LE DERIVATE
3.1.2
Un Primo Approccio alla Stima della Derivata
Abbiamo descritto la funzione derivata in termini di rapidità di cambiamento
e di pendenza dato un punto a nel dominio di f.
Data una funzione f ed un valore dell’ingresso x = a,
f0 (a) è il tasso di variazione istantanea di f rispetto ad x nel
punto x = a.
In linguaggio grafico,
f 0 (a) è la pendenza del grafico di f nel punto x = a.
Vogliamo in questo paragrafo dare una breve occhiata, più da
vicino,alla derivata di una funzione in un punto.
Stima di f’(a). La Pendenza di un Grafico in un Punto,
Tangente.
Per una retta ax + b la ricerca della pendenza è pura routine. Essa infatti,
come abbiamo visto, non è altro che a, il coefficiente angolare della retta
stessa. Per una curva qualsiasi la questione è più complicata, ma anche più
interessante.
La pendenza di una curva in un punto P può essere pensata, come già detto,
come la pendenza della retta tangente alla curva nel punto P , cioè il coefficiente
angolare della retta passante per P che “punta nella direzione della curva” in
P.
La definizione è molto vaga per essere soddisfacente dal punto di vista
matematico, ma ci permette, per ora, di illustrare l’idea e di calcolarne “con
buona approssimazione” il valore per molte delle funzioni che incontriamo in
questo corso.
Esempio 56 Sia f (x) = x2 . Usare la retta tangente per stimare il valore di
f 0 (1) e di f 0 (−1.5) . Interpretare i risultati come rapidità di cambiamento.
Soluzione. Ecco il grafico di f insieme a quello di due ragionevoli candidati
ad essere rette tangenti per x = 1 ed x = −1.5
4
3
2
1
0
-1
-1
0x
1
2
Grafico di f (x) = x2 e due rette tangenti
3.1. LA DERIVATA COME VARIAZIONE
103
Possiamo adesso stimare la pendenza delle due rette tangenti direttamente
dal grafico. La retta passante per (1, 1), per esempio, sembra salire di 2 unità
mentre la variabile indipendente si sposta di 1, così la pendenza è 2. In modo
simile la retta tangente ad x = −1.5 sembra avere pendenza di circa −3. Ne
concludiamo che
f 0 (1) ≈ 2 e f 0 (−1.5) ≈ −3
Nel linguaggio della rapidità di cambiamento i risultati significano che (i)
per x = 1, y cresce due volte più rapidamente di x, e (ii) per x = −1.5, y tre
volte più rapidamente della crescita di x.
¥
Tracciare la retta tangente è un modo per stimare il valore della derivata. La
strategia funziona perché nell’intorno del punto in questione, il grafico e la retta
tangente sono quasi indistinguibili. Rimane il problema non sempre banale di
essere capaci di tracciare una retta tangente in modo accurato, prescindendo
dalla conoscenza della sua equazione (per ora).
Un’altra strategia, spesso più conveniente, che si può usare disponendo della possibilità di software per il disegno di grafici, è quella dell’ingrandimento
nell’intorno del punto in questione, a volte in modo ripetuto, finché il grafico
stesso appare essere una linea retta. Una volta che il grafico appare come una
retta è semplice stimarne la pendenza.
Esempio 57 Sia f (x) = x2 . Stimare il valore di f 0 (1) con il metodo dell’ingrandimento. Usare il risultato per scrivere l’equazione della retta tangente nel
punto x = 1.
Soluzione. Ingrandendo successivamente nell’intorno del punto (1, 1) da i
seguenti grafici
1.2
2
1.1
1
1
0.9
0
0.6
0.8
x1
1.2
1.4
Grafico di x2 per x ∈ [0.5, 1.5]
0.8 0.9
x1
1.1
Grafico di x2 per x ∈ [0.9, 1.1]
Nel secondo disegno il grafico appare come una linea retta e la sua pendenza
appare essere 2 perché y varia da 0.8 a 1.2 mentre x varia da 0.9 a 1.1. La retta
in questione è dunque la retta di coefficiente angolare 2 passante per il punto
(1, 1) . La sua equazione è y = 2 (x − 1) + 1 = 2x − 1.
¥
Quando Funziona l’Ingrandimento.
104
CAPITOLO 3. LE DERIVATE
La strategia appena illustrata funziona quasi sempre. Ingrandire ripetutamente il grafico della maggior parte delle funzioni f nell’intorno di un qualsiasi
punto (a, f (a)) del grafico alla fine produce un disegno che appare essere un
retta di coefficiente angolare f 0 (a) . Una funzione con questa proprietà è anche
chiamata localmente lineare per x = a (Non è una definizione formale, solo
una frase descrittiva). La linearità locale dice che in effetti una funzione f
“si comporta come una retta” in un intorno del punto x = a e quindi ha una
pendenza ben definita in x = a.
L’esempio precedente mostra che f (x) = x2 è localmente lineare per x = 1.
Vediamo un esempio con funzioni trigonometriche.
Esempio 58 Dire se f (x) = sin x è localmente lineare nel punto x = 1.4.
Qual’è il valore di f 0 ?
Soluzione. Ecco due viste del grafico della funzione seno nell’intorno del
punto (1.4, sin 1.4) ≈ (1.4, 0.9854).
0.988
0.99
0.986
0.98
0.984
0.97
0.982
1.3
1.34 1.36 1.38 1.4
x 1.42 1.44 1.46 1.48 1.5
Grafico di sin x, x ∈ [1.3, 1.5]
1.39
1.4
x
1.41
1.42
Grafico di sin x, x ∈ [1.38, 1.42]
nel secondo grafico, la curva del seno è quasi retta. Per stimare la pendenza nel
punto P = (1.4, sin 1.4) usiamo due punti presi dal grafico. Prendendo x = 1.38
e x = 1.42 si trova che il valore (ovviamente approssimato) della pendenza è
(0.989 − 0.982) / (1.42 − 1.38) ≈ 0.175. Usando la notazione delle funzioni si ha
¥
cioè f 0 (1.4) ≈ 0.175.
Quando Non Funziona l’Ingrandimento: Nonlinearità Locale.
Non tutte le funzioni sono ovunque localmente lineari. Uno “spigolo” nel
grafico non può essere sempre lisciato da un ripetuto ingrandimento locale del
grafico. In tale punto la derivata non esiste ed il nostro modello di rappresentazione non dà risposte.
Esempio 59 Sia f (x) = |x| . Dire se esiste f 0 (0) . Dire se esiste f 0 (a) se
a 6= 0.
3.1. LA DERIVATA COME VARIAZIONE
105
Soluzione. Ecco il risultato di un ingrandimento intorno all’origine.
1
0.1
0.8
0.08
0.6
0.06
0.4
0.04
0.2
0.02
0
0
-0.2
-0.02
-0.4
-0.04
-0.6
-0.06
-0.8
-1
-0.08
-0.8 -0.6 -0.4 -0.2
x0
0.2 0.4 0.6 0.8
1
Grafico di |x| per x ∈ [−1, 1]
-0.1
-0.08
-0.04
x0
0.02 0.04 0.06 0.08 0.1
Grafico di |x| per x ∈ [−0.1, 0.1]
Come si vede, l’ingrandimento non ha alcune effetto sullo ”spigolo” nell’origine. Ingrandire ancora non servirebbe, lo spigolo rimane e perciò f 0 (0) non
esiste.
D’altra parte, per a 6= 0 il grafico è già una retta (con coefficiente angolare ±1),
così non vi è alcun problema nel valutare le derivate:
f 0 (a) = 1 se a > 0 ;
f 0 (a) = −1 se a < 0 .
A parole: la funzione f (x) = |x| non è localmente lineare per x = 0, ma lo è in
tutti gli altri punti.
¥
NOTA: In tutto questo paragrafo ”ingrandire” significa ingrandire dello
stesso fattore rispetto ai due assi cartesiani. Questo fatto non è solo di tipo
tecnico. Ingrandire con fattori di scala diversi rispetto ai due assi porterebbe a
delle distorsioni del grafico che potrebbero far perdere informazioni.
Considerate, per esempio, l’esempio precedente. Ingrandendo ripetutamente,
ma solo nella direzione dell’asse x (per es. un fattore 4 lungo x ed 1 lungo y)
finirebbe gradualmente col far sembrare il grafico orizzontale e quindi derivabile
(Provare).
Il metodo di ingrandire o di disegnare tangenti al grafico in un punto permette di stimare f 0 (a) per vari valori dell’ingresso a. Mettendo insieme le informazioni che se ne ricavano si può provare a disegnare il grafico della funzione
derivata.
Esempio 60 Provare a disegnare il grafico di f 0 (x), essendo f (x) = x2 .
Soluzione. Nell’esempio relativo alla funzione f (x) = x2 si è stimato che
= 2 e f 0 (−1.5) = −3. Per la simmetria del grafico della funzione rispetto
all’asse y si può affermare che f 0 (−1) = −2 e f 0 (−1.5) = +3 e f 0 (0) = 0.
Tracciando questi punti su di un grafico si nota che essi sono allineati sulla
retta y = 2x.
f 0 (1)
106
CAPITOLO 3. LE DERIVATE
4
2
-2
-1
0
1x
2
-2
-4
Grafico di f 0
¥
Esempio 61 Sia f (x) = ex . Usare il metodo delle rette tangenti per valutare
f 0 . Cercare infine di valutare una formula per f 0 (x) .
Soluzione. Disegniamo il grafico di f (x) = ex e cerchiamo, usando matita
e righello di valutare la pendenza delle tangenti nei punti marcati.
8
6
4
2
-2
-1
0
1x
2
Grafico di f (x) = ex
Con un po’ di accuratezza si possono trovare i seguenti risultati
Stima grafica della derivata di ex
x
−2
−1
0
1
2
y
0.135 0.368 1.0 2.718 7.389
Pendenza in (x, y) 0.1
0.4
1.0 2.7
7.4
Già ad un primo esame si vede come i valori della pendenza nei punti dati
approssimino con grande precisione i valori della funzione negli stessi punti.
3.1. LA DERIVATA COME VARIAZIONE
107
Infatti, il risultato importante che rende unica la funzione esponenziale ex è il
seguente.
Se f (x) = ex allora si ha che f 0 (x) = ex .
In altre parole, f (x) = ex risolve l’equazione differenziale f 0 (x) = f (x) .
Questa importante proprietà è ciò che rende la funzione esponenziale ex una
delle funzioni più importanti ed utili.
¥
108
3.1.3
CAPITOLO 3. LE DERIVATE
Esercizi
1. Un aeroplano decolla da un aeroporto e, 60 minuti dopo atterra in un
altro aeroporto distante 600 km. Sia t il tempo, misurato dal momento
del decollo, x (t) la distanza orizzontale percorsa e y (t) l’altezza dell’aeroplano.
(a) Qual’è il significato fisico di x0 (t) ? Disegnate dei grafici plausibili
di x (t) e x0 (t) .
(b) Qual’è il significato fisico di y 0 (t) ? Disegnate dei grafici plausibili
di y (t) e y0 (t) .
2. Supponiamo che sia f (x) = x3 − 5x2 + x − 1 e g (x) = x3 − 5x2 x + 4.
(a) Spiegare perché f 0 (x) = g 0 (x) per ogni valore di x. [Sugg: Come
sono correlati i grafici di f e g ?]
(b) Trovare una funzione h tale che h (0) = 3 e tale che h0 (x) = f 0 (x) .
3. Siano f (x) = 5, g (x) = x, h (x) = −2x. Calcolare f 0 (11) , g 0 (33) , h0 (−37) .
4. Supponiamo che siano f (x) = x − 2, g (x) = 4x + 1.
(a) Disegnare f e g sullo stesso sistema d’assi.
(b) Mostrare che f 0 (x) ≤ g 0 (x) per tutti i valori di x.
(c) Mostrare che il principio delle corse implica che f (x) ≤ g (x) per
tutti gli x ≥ −1.
5. Cosa dice il principio delle corse sulla relazione tra f (x) e g (x) per
x ≤ 1?
6. Interpretare ogni affermazione sottostante in termini di funzioni e sue
derivate. In ogni situazione indicare chiaramente quale è la funzione, che
significa la variabile e quali sono le unità di misura appropriate.
(a) Il prezzo di un prodotto diminuisce con l’aumentare della produzione.
(b) La richiesta di un nuovo prodotto diminuisce con il tempo.
(c) La forza lavoro cresce oggi più lentamente di cinque anni fa.
(d) Il costo dell’assistenza sanitaria continua a crescere, ma più lentamente negli ultimi cinque anni.
(e) Durante gli scorsi due anni il consumo di energia in Italia è diminuito.
7. Una Compagnia deve decidere il budget per ricerca e sviluppo di un nuovo
prodotto. Sia x l’ammontare investito in R&S e T il tempo occorrente
perché il prodotto raggiunga il mercato.
(a) Dare unità ragionevoli a T ed x. Cosa rappresenta T 0 in queste unità?
(b) Dare una interpretazione economica a T 0
3.1. LA DERIVATA COME VARIAZIONE
109
(c) Vi aspettate un T 0 positivo o negativo? Spiegare la risposta.
8. L’altezza di un sasso in metri, t secondi dopo essere stato lanciato è data
da h (t) = −4.91t2 ++13t+25; la sua velocità è data da v (t) = −9.82t+13.
(a) Da quale altezza è stata lanciato il sasso?
(b) Qual’era la velocità iniziale del sasso?
(c) L’altezza del sasso al tempo t = 2 è maggiore o minore?
(d) Per quale valore del tempo il sasso raggiunge l’altezza massima?
Quanto vale l’altezza?
(e) Quanto tempo sta il sasso in aria?
9. Supponiamo che sia f (x) = g (x) + 3 e che f 0 (x) esista per tutti gli x.
(a) Spiegare come sono correlati i grafici di f e g.
(b) Spiegare come sono correlati i grafici di f 0 e g 0
(c) Sia h (x) = f (x) + k con k costante. Come è correlato il grafico di
h0 con quello di f 0 ?
10. Sia f (x) = sin x e g (x) = cos x.
(a) Come sono correlati tra loro i grafici di f e di g ?
(b) Come sono correlati tra loro i grafici di f 0 e di g 0 ?
11. Sia g (x) = f (x + 3) e supponiamo che f 0 (x) esista per tutti gli x.
(a) Spiegare come sono correlati i grafici di f e g.
(b) Spiegare sono correlati tra loro i grafici di f 0 e di g 0 .
(c) Se f 0 (2) = 4 quanto vale g 0 (−1) ?
(d) Sia h (x) = f (x + k) con k costante. Come è correlato il grafico di
h0 con quello di f 0 ?
12. Sia g (x) = 3f (x) e supponiamo che f 0 (x) esista per tutti gli x.
(a) Spiegare come sono correlati i grafici di f e g.
(b) Spiegare sono correlati tra loro i grafici di f 0 e di g 0 .
(c) Se f 0 (−1) = 2, spiegare perché g 0 (−1) = 6.
(d) Sia h (x) = k f (x) con k costante. Come è correlato il grafico di h0
con quello di f 0 ?
13. Supponiamo che f sia periodica di periodo 4. Spiegare perché la funzione
derivata f 0 è anch’essa periodica con lo stesso periodo.
14. Sia f una funzione tale che f 0 (3) = −2
110
CAPITOLO 3. LE DERIVATE
(a) Supponiamo f pari. Spiegare perché f 0 (−3) = 2. [Sugg.: pensate
al grafico di una funzione pari.]
(b) Supponiamo f dispari. Quanto vale f 0 (−3) ?
15. Supponiamo che f e g siano definite entrambe nell’intervallo [a, b] , che
sia f (a) = g (a) e che f 0 (x) ≤ g 0 (x) per tutti gli x ∈ [a, b] .
(a) Spiegare perché f (b) ≤ g (b) .
(b) Supponiamo f (b) = g (b) . Che cosa implica questo sulle derivate f 0
e g0 ?
16. Supponiamo che f e g siano definite entrambe nell’intervallo [a, b] , che
sia f (a) = g (a) e che f 0 (x) ≤ g 0 (x) per tutti gli x ∈ [a, b] . Usare il
principio delle corse per spiegare che f (x) − f (a) ≤ g (x) − g (a) per tutti
gli x ∈ [a, b] .
17. Sia f (1) = −2 e f 0 (x) ≤ 3 per tutti gli x ∈ [−10, 10] .
(a) Mostrare che f (2) ≤ 1.
(b) Mostrare che f (5) ≤ 10.
(c) Mostrare che f (0) ≥ −5.
(d) Può essere f (9) < 31 ? Spiegare la risposta.
(e) Può essere f (−5) > −23 ? Spiegare la risposta.
(f) Può essere f (4) = 8 ? Giustificare la risposta.
(g) Può essere f (−7) = −25 ? Giustificare la risposta.
(h) Può essere f (8) = −25 ? Giustificare la risposta.
18. Sia f (1) = 3 e f 0 (x) ≥ 2 per tutti gli x ∈ [0, 5] .
(a) Mostrare che f (4) ≥ 9.
(b) Mostrare che f (0) ≤ 1.
19. Supponiamo che sia f (2) = 1 e −4 ≤ f 0 (x) ≤ 3 per tutti gli x ∈ [−10, 10] .
(a) Trovare una stima superiore ed una inferiore per f (6) ;
(b) Trovare una stima superiore ed una inferiore per f (−5) .
20. Supponiamo sia f (0) = 2 e |f 0 (x)| ≤ 1 per tutti gli x ∈ [−5, 5] .
(a) Trovare una stima superiore ed una inferiore per f (1) ;
(b) Trovare una stima superiore ed una inferiore per f (−3) .
21. Supponiamo che sia f (2) = 1 e f 0 (x) ≤ −3 per tutti gli x ∈ [−10, 10] .
(a) Che cosa implica il principio delle corse per il valore di f (4) ?
3.1. LA DERIVATA COME VARIAZIONE
111
(b) Che cosa implica il principio delle corse per il valore di f (−2) ?
22. Sia f 0 (x) ≤ 0 per tutti gli x ∈ (2, 9) . Spiegare perché f (3) ≥ f (7) .
23. Sia f 0 (x) > 0 per tutti gli x ∈ (2, 9) . Spiegare perché f (4) < f (8) .
24. Supponiamo che sia f (−1) = −2 e che f 0 (x) sia la funzione disegnata qui
sotto
4
2
-4
-3
-2
-1
1
2x
3
4
-2
-4
Grafico di f 0
Usare il principio delle corse per rispondere alle seguenti domande.
(a) Può essere f (3) = −6 ? Giustificare la risposta.
(b) Può essere f (3) = 2 ? Giustificare la risposta.
(c) Mostrare che, nell’intervallo [−4, 4] , la funzione raggiunge il suo valore massimo nel punto x = 4. [Sugg. Mostrare che 0 < f (−4) −
f (−3) < 6 e che f (1) − f (−2) > 6].
(d) Per quale valore di x nell’intervallo [−4, 4] la f raggiunge il suo
minimo ?
25. Sia k un numero reale e che f sia una funzione tale chef 0 (x) ≤ k per tutti
gli x ∈ [a, b] . Mostrare che f (x) ≤ k (x − a) + f (a) per tutti gli x ∈ [a, b] .
26. Sia f una funzione definita nell’intervallo [a, b] e che f (a) = c .
(a) Supponiamo sia f 0 (x) ≤ 0 per tutti gli x ∈ [a, b] Usare il principio
delle corse per mostrare che f (x) ≥ c per tutti gli x ∈ [a, b] .
(b) Supponiamo sia f 0 (x) ≤ 0 per tutti gli x ∈ [a, b] Usare il principio
delle corse per mostrare che f (x) ≥ c per tutti gli x ∈ [a, b] .
(c) Usare (a) e (b) per mostrare che se f 0 (x) = 0 per tutti gli x ∈ [a, b]
allora f è costante in tutto l’intervallo [a, b] .
27. Supponiamo che f 0 (x) = g 0 (x) per tutti gli x ∈ [a, b]. Usare l’esercizio
precedente per mostrare che esiste una costante C tale che g (x) = f (x) +
C per tutti gli x ∈ [a, b].
112
CAPITOLO 3. LE DERIVATE
28. Sia f (x) =
√
x.
(a) Usare il metodo dell’ingrandimento per stimare f 0 (1/4) , f 0 (1),
f 0 (9/4), f 0 (4) , f 0 (25/4) e f 0 (9) .
(b) Usare i risultati di (a) per disegnare un grafico di f 0 nell’intervallo
[0, 9] .
(c) Perché non è definita f 0 (−1) ? Perché non è definita f 0 (0) ? Qual’è
il dominio di f 0 ?
(d) Usare i risultati precedenti per tentare di trovare l’espressione algebrica di f 0 (x) .
29. Sia f (x) = x3 e g (x) = x1/3 .
(a) Usare il metodo dell’ingrandimento per stimare f 0 (0), f 0 (1/2), f 0 (1),
f 0 (3/2), f 0 (2) .
(b) Usare i risultati di (a) per disegnare un grafico di f 0 nell’intervallo
[−2, 2] .[Sugg.: Perché f 0 (−1) = f 0 (1) ?].
(c) Usare i risultati di (a) e (b) per tentare di trovare l’espressione
algebrica di f 0 (x) .
(d) Stimare g 0 (−1) e g 0 (1) .
(e) Perché non è definita g 0 (0) ? Qual è il dominio di g 0 ? Qual’è il
dominio di g ?
(f) Si può mostrare che f 0 (4) = 48. Usare questo dato per calcolare
g 0 (64) . [Sugg: Come sono correlati i grafici di f e g ?]
30. Sia f (x) = 1/x
(a) Usare il metodo dell’ingrandimento per stimare f 0 (1/4), f 0 (1/2),
f 0 (1), f 0 (2), f 0 (3) .
(b) Usare i risultati di (a) per disegnare un grafico di f 0 sugli intervalli
[−3, 0) e (0, 3] .
(c) Usare i risultati di (a) e (b) per tentare di trovare l’espressione
algebrica di f 0 (x) .
31. Sia f (x) = ex .
(a) Usare il metodo dell’ingrandimento per stimare f 0 (−1), f 0 (0), f 0 (1),
f 0 (1.5), f 0 (2) .
(b) Usare i risultati di (a) per disegnare un grafico di f 0 sull’intervallo
[−1, 2] .
(c) Usare i risultati di (a) e (b) per tentare di trovare l’espressione
algebrica di f 0 (x) . [Sugg.: valutare f (x) nei punti −1, 0, 1, 1.5, 2.]
32. Sia f (x) ln x
3.1. LA DERIVATA COME VARIAZIONE
113
(a) Usare il metodo dell’ingrandimento per stimare f 0 (1/10) , f 0 (1/5),
f 0 (1/2), f 0 (1) , f 0 (2) , f 0 (5) .
(b) Usare i risultati di (a) per disegnare un grafico di f 0 sull’intervallo
(0, 5] .
(c) Usare i risultati di (a) per tentare di trovare l’espressione algebrica
di f 0 (x)
33. Sia f (x) = sin x.
(a) Usare il metodo dell’ingrandimento per stimare f 0 (0) , f 0 (π/6), f 0 (π/4),
f 0 (π/3) , f 0 (π/2) e f 0 (π) .
(b) Usare la simmetria della funzione seno per calcolare le derivate nei
punti f 0 (2π/3) , f 0 (3π/4) e f 0 (5π/6) . Controllate le risposte col
metodo dell’ingrandimento.
(c) Usare i risultati di (a) per tentare di trovare l’espressione algebrica
di f 0 (x) .
34. Sia f (x) = cos x.
(a) Usare il metodo dell’ingrandimento per stimare f 0 (0) , f 0 (π/6), f 0 (π/4),
f 0 (π/3) , f 0 (π/2) e f 0 (π) .
(b) Usare i risultati di (a) per tentare di trovare l’espressione algebrica
di f 0 (x) .
35. Siano f (x) = ex e g (x) = ln x .
(a) Usare il metodo dell’ingrandimento per il grafico di f nell’intorno del
punto del grafico (0, 1) .Qual’è la pendenza della retta?
(b) Usare il metodo dell’ingrandimento per il grafico di g nell’intorno del
punto del grafico (0, 1) .Qual’è la pendenza della retta?
36. Siano f (x) = 10x e g (x) = log10 x .
(a) Usare il metodo dell’ingrandimento per il grafico di f nell’intorno del
punto del grafico (0, 1) .Qual’è la pendenza della retta?
(b) Usare il metodo dell’ingrandimento per il grafico di g nell’intorno del
punto del grafico (0, 1) .Qual’è la pendenza della retta?
(c) Come sono collegate tra loro i valori in (a) ed in (b) ? Quale variante
della legge nell’Esempio (61) vale in questa situazione?
37. Sia f (2) = 4 e f 0 (x) =
√
x3 + 1 per x ≥ −1
(a) Trovare l’equazione della retta tangente a f nel punto x = 2.
(b) Indichiamo con l la retta in (a) . Il valore l (0) sottostima o sovrastima il valore di f (0)? Giustificare la risposta.
114
CAPITOLO 3. LE DERIVATE
(c) Il valore l (3) sottostima o sovrastima il valore di f (3)? Giustificare
la risposta.
38. Per ognuna delle coppie di funzioni seguenti, scegliere la costante A in
modo tale che sia f 0 (x) = Ag (x) per ogni x nel dominio di g.
(a) f (x) = x3 , g (x) = x2 .
√
(b) f (x) = x, g (x) = x−1/2 .
(c) f (x) = sin x , g (x) = cos x.
(d) f (x) = cos x , g (x) = sin x.
(e) f (x) = ex , g (x) = ex .
(f) f (x) = ln x, g (x) = 1/x.
3.2. LA GEOMETRIA DELLE DERIVATE.
3.2
115
La Geometria delle Derivate.
La relazione geometrica che lega una funzione f e la sua derivata f 0 è semplice
da esplicitare.
Per ogni valore dell’ingresso a, f 0 (a) è il valore del coefficiente angolare
della retta tangente al grafico di f nel punto (a, f (a)) .
Questa affermazione, innocua all’apparenza, è una delle più importanti di
questo volume. I prossimi paragrafi (e di fatto la maggior parte di questo libro)
ne esplorano significato, implicazioni e conseguenze. Inizieremo la nostra analisi
attraverso lo studio approfondito di un esempio.
Confronto tra i Grafici di f e di f ’. Consideriamo i grafici (dati)
di una funzione f e della sua derivata f 0 (per il momento non daremo la formula
esplicita per le due funzioni). Tre punti interessanti sono stati segnalati sui due
grafici. I tre punti sui due grafici hanno la stessa coordinata x. Chiamiamo i
tre punti A, B, C e A0 , B 0 , C 0 rispettivamente.
4
15
2
-2
-1
1
x 2
3
10
0
-2
-6
-8
Grafico di f
5
-2
-1
0
1
x 2
3
-5
Grafico di f 0
Il grafico si f 0 ci dice come si comportano le pendenze delle rette tangenti
al grafico di f . Per esempio, in B il grafico di f sembra avere pendenza −6 I;
per questa ragione, il grafico di f 0 ha altezza −6 in B 0 .
Osserviamo le diverse relazioni geometriche tra i due grafici e introduciamo un
po’ di nomenclatura.
Il segno di f 0 . Il grafico di f cresce a sinistra a sinistra del punto A, scende
tra A e C, cresce ancora dopo C. Il segno di f 0 ci dice se il coefficiente angolare
della retta tangente è positivo o negativo, cioè se la retta tangente punta verso
l’alto o verso il basso.. Nei punti A0 e C 0 I la funzione f 0 cambia di segno,
quindi in A e C la tangente ad f cambia direzione.
Cosa accade all’esterno. Il disegno suggerisce che a sinistra di A il grafico
di f scenda verso il basso e a destra di C salga. Che c
osa accade del grafico
0
0
0
di f negli stessi intervalli? A destra di C , f è positiva e crescente, mentre a
sinistra di A0 è positiva e decrescente.
Controllate, per
esercizio, l’affermazione.
A0 e C 0 corrispondono
radici di f 0 .
a
116
CAPITOLO 3. LE DERIVATE
Punti di massimo, minimo e stazionari. I punti A e C di coordinate
approssimativamente (−1.1, 4) e (1.8, −8) dove il grafico di f ha tangente orizzontale sono punti di notevole interesse. Essi indicano, in questa finestra del
grafico, punti “alti” e punti “bassi” del grafico stesso.
Volendo esprimere questa situazione in linguaggio matematico diremo che il
punto del dominio x = 1.1 è un punto di massimo locale per f , la corrisponde uscita f (−1.1) ≈ 4 è chiamato un valore di massimo locale di f .
Analogamente in C. Il punto x = 1.8 è chiamato punto di minimo locale e
f (1.8) ≈ −8 è il corrispondente valore di minimo locale per f (l’aggettivo
locale si riferisce al fatto che stiamo esaminando ciò che accade intorno al punto
e non globalmente su tutto il grafico). Gli ingressi x dei punti A e C sono anche
genericamente chiamati punti stazionari per f . I corrispondenti punti A0 e
C 0 sul grafico di f 0 hanno la proprietà di avere coordinata y = 0,sono cioè radici
dell’equazione f 0 (x) = 0.
Altri punti stazionari? A e C sono gli unici punti stazionari di f. Il disegno non lo dice. Esso mostra solo il comportamento della funzione nell’intervallo
[−2.5, 3.5] ; altri punti stazionari potrebbero essere fuori di questo intervallo.
Concavità e convessità. Il punto B, di coordinata circa x = 0.33 viene
chiamato punto di flesso per f . In B il grafico di f cambia la propria
direzione di concavità , da concavo a convesso. Il punto B ha un’altra
proprietà geometrica (locale) importante. E’ il punto del grafico con la maggiore
pendenza.
Il corrispondente punto B 0 sul grafico di f 0 è facile da individuare; è un
punto di minimo locale per f 0 . Più avanti useremo questa proprietà e un po’ di
algebra per trovare l’esatto valore dell’ingresso di B.
Che cosa dice f ’ a proposito di f.
Interpretare la funzione derivata f 0 in termini di coefficienti angolari delle
rette tangenti al grafico di f ha molte implicazioni di notevole importanza che
indichiamo qui di seguito.
(NOTA: Molte idee in questo paragrafo dipendono dal fatto che sia f che f ’ si
comportano “ragionevolmente bene”. Con questa espressione intendiamo il fatto che
né il grafico di f né quello di f ’ mostrano salti, spigoli o rotture. Ogni funzione f la
cui funzione derivata f ’ è continua, cioè ha un grafico senza rotture, è buona per noi
a questo livello. Fortunatamente, la maggior parte delle funzioni che ci interesseranno
saranno “buone” in questo senso. Andando avanti nel corso chiariremo meglio cosa
significa “buone” e perché è importante.)
Crescente o Decrescente.
Una funzione f è detta crescente se (osservandola da sinistra verso destra) il suo grafico sale, e decrescente se il suo grafico scende. La seguente
definizione trascrive queste idee naturali in linguaggio analitico.
Definizione 62 Sia I l’intervallo (a, b) . Una funzione f è crescente su I se
f (x1 ) < f (x2 )
per
a < x1 < x2 < b .
3.2. LA GEOMETRIA DELLE DERIVATE.
117
f è decrescente su I se
f (x1 ) > f (x2 )
per
a < x1 < x2 < b .
( Se f (x1 ) ≤ f (x2 ) per x1 < x2 allora f è detta non decrescente su
I; se f (x1 ) ≥ f (x2 ) per x1 < x2 allora f è detta non crescente su I. In
entrambi i casi, in modo generico diremo che f è monotona su I ).
La derivata ci permette di determinare dove la funzione cresce o decresce
su di un intervallo I.
Fatto. Se f 0 (x) > 0 per tutti gli x ∈ I allora f cresce in I.
Se f 0 (x) < 0 per tutti gli x ∈ I allora f decresce in I.
Questo fatto sembra essere ragionevole. Affermare che f 0 (x) > 0 significa
dire che la retta tangente al grafico di f nel punto x punta verso l’alto e (con
un po’ di fortuna) anche il grafico di f .Il principio delle corse rende il fatto
ancora più evidente: se un’auto f ha velocità positiva, allora corre “in avanti”.
Anche se il fatto suona plausibile, la sua dimostrazione rigorosa richiede la
messa in campo di uno dei teoremi più importanti di questo corso: il teorema
del valor medio (che vedremo più avanti).
Comportamento in un punto. Spesso diremo che la “funzione cresce (o
decresce) in un dato punto. Dire ad esempio che f cresce per x = 3 significa
dire che f cresce su di un qualche intervallo - per quanto piccolo possa essere contenente il punto x = 3. Con questa notazione lessicale possiamo riscrivere il
fatto precedente nel seguente modo.
Fatto. Se f 0 (a) > 0 allora f cresce in x = a
Se f 0 (a) < 0 allora f decresce in x = a
Nel punto x = 1, per esempio, f 0 (1) < 0. Il Fatto ci dice - ed il disegno
conferma - che per x = 1 il grafico di f discende.
Fare attenzione Il precedente fatto NON implica che se f cresce allora
0
f (a) > 0. Infatti
Esempio 63 Dove è crescente la funzione f (x) = x3 ? Dove è f 0 (x) > 0 ? Che
cosa accade per x = 0 ?
Soluzione. Come suggerisce il grafico
1
0.5
-1
-0.5
0
0.5
x
-0.5
-1
Grafico di f (x) = x3
1
118
CAPITOLO 3. LE DERIVATE
la funzione x3 cresce ovunque. Il grafico suggerisce anche che f 0 (x) > 0 se
x 6= 0 ma che f 0 (x) = 0 per x = 0.
La Derivata di una Funzione Crescente. Che cosa si può dire della
funzione derivata f 0 dove f cresce? La risposta è nel seguente fatto
Fatto. Se f cresce per x = a allora si ha f 0 (a) ≥ 0;
se f decresce per x = a allora si ha f 0 (a) ≤ 0.
La derivata di una funzione crescente deve essere non negativa ma non
necessariamente strettamente positiva.
Punti di Massimo, Punti di Minimo e Punti Stazionari:
Definizioni Formali.
Il punto A sul primo grafico (vedi pagina 115 ) corrisponde ad un massimo
locale ma non globale per f . Per continuare a usare senza fraintesi il linguaggio
tecnico della matematica abbiamo bisogno di definizioni chiare.
Definizione 64 Sia f una funzione e x0 un punto del dominio.
• x0 è un punto stazionario per f se f 0 (x0 ) = 0 .
• x0 è un punto di massimo relativo (o locale) per f se f (x0 ) ≥ f (x)
per tutti gli x in qualche intervallo aperto contente x0 . Il numero f (x0 ) è un
valore di massimo relativo per f.
• x0 è un punto di massimo assoluto (o globale) per f se f (x0 ) ≥ f (x)
per tutti gli x nel dominio di f . Il numero f (x0 ) è il valore di massimo
assoluto per f.
(I punti di minimo relativo (o locale) e assoluto (o globale) sono definiti in
maniera analoga).
Alcune sottigliezze lessicali hanno bisogno di essere puntualizzate:
Punti e Valori. I punti di massimo o minimo (relativo o assoluto) sono
gli ingressi per le funzioni; i valori di massimo o minimo sono le corrispondenti
uscite. La differenza, sebbene importante, viene a volte sorvolata parlando
informalmente.
Relativo e Assoluto (Globale e Locale). In un punto di massimo
locale, una funzione f può o meno assumere un valore di massimo globale. Lo
stesso ovviamente per un punto di minimo.
Valori estremi. La parola estremo che può significare sia valore massimo che minimo è spesso usata. Diremo, per esempio, che per la funzione
dell’esempio precedente, i punti A e C corrispondono ad estremi di f .
Tornando al grafico dell’esempio, l’intuizione geometrica ci dice che in un
punto di massimo o di minimo locale un grafico “liscio” debba avere tangente
orizzontale. Più succintamente
Fatto. In un grafico “liscio”ogni punto di massimo e di minimo
locale x0 è un punto stazionario, cioè una radice di f 0 ,
quindi soddisfa l’equazione f 0 (x) = 0.
Questo fatto ha un valore pratico di notevole portata. Il Fatto ci dice che
per trovare i massimi e minimi relativi di f , possiamo limitarci a cercare tra le
3.2. LA GEOMETRIA DELLE DERIVATE.
119
radici di f 0 Ogni radice è un punto stazionario e quindi un possibile candidato a
massimo o minimo (ricordo che un punto stazionario può anche essere un flesso
orizzontale del grafico).
Nell’esempio che segue cercheremo di mostrare come individuare tutte le
possibilità.
Esempio 65 Il grafico di una funzione f 0 appare come segue. Il grafico di
f non è mostrato (per ora). Tre punti di particolare interesse sono mostrati
(−1, 0) , (0, 0) , (1, 0) . In quali punti, ammesso che esistano, f ammette minimo e massimo locale? Perché
3
2
1
0
-1
-2
-1
-0.5
0x
0.5
1
1.5
Grafico di f 0
Soluzione. I tre punti, di coordinate x = −1, x = 0, x = 1 sono radici
dell’equazione f 0 (x) = 0 e corrispondono quindi a punti stazionari di f . Che
tipo di punto stazionario? La chiave per risolvere il problema è quella di studiare
il segno della derivata intorno ad ogni punto stazionario. Osserviamo i punti
uno alla volta.
[x = −1] . A sinistra di x = −1 si ha che f 0 (x) > 0. Quindi, per quanto
affermato precedentemente, la funzione f cresce finché x = −1. Passato il punto
è f 0 (x) < 0 così che f decresce immediatamente dopo x = −1. Questo significa
che f ha un massimo locale in x = −1.
[x = 1] . Consideriamo i valori della f 0 per valori di x vicini ad x = 1. Il
grafico mostra che se x < 1 allora f 0 (x) < 0, e che f 0 (x) > 0 se x > 1. Allora,
ragionando come sopra, si ha che la funzione decresce a sinistra di x = 1 e
cresce a destra. Questo significa che x = 1 è un punto di minimo locale.
[x = 0] In questo punto il grafico mostra che f 0 (x) < 0 sia a sinistra che a
destra del punto x = 0. Allora f decresce sia prima che dopo il punto x = 0.
Ne segue che x = 0 non può essere né un massimo né un minimo. E’ quindi un
flesso orizzontale nel grafico di f .
Ecco, per finire, un possibile grafico di f .
120
CAPITOLO 3. LE DERIVATE
2
1
0
-1
-2
-1
-0.5
0x
0.5
1
1.5
Grafico di f
Per quanto riguarda i punti stazionari possiamo allora affermare che:
Fatto (Test della derivata prima). Supponiamo che si abbia f 0 (x0 ) = 0.
• Se f 0 (x) < 0 per x < x0 e f 0 (x) > 0 per x > x0 , allora x0 è un punto di
minimo locale.
• Se f 0 (x) > 0 per x < x0 e f 0 (x) < 0 per x > x0 , allora x0 è un punto di
massimo locale.
Il prossimo esempio mostra cosa accade in un grafico non “liscio”.
Esempio 66 La funzione f (x) = |x| ha un minimo locale (e globale) nel punto
x = 0, ma non un punto stazionario..
Soluzione. Il grafico mostra il perché
|x|
-1
0
x
Grafico di f (x) = |x| ;
x = 0 è un minimo locale.
1
3.2. LA GEOMETRIA DELLE DERIVATE.
121
Nel punto x = 0 il grafico ha uno spigolo e quindi non ammette né retta
tangente né una pendenza ben definita. Nel linguaggio funzionale possiamo dire
che f 0 (0) non esiste.
Concava o Convessa ?
Abbiamo introdotto in modo informale le proprietà flesso, concavità e convessità usando il linguaggio grafico. Vogliamo adesso dare una definizione
analitica formale.
Definizione 67 Il grafico di una funzione f è convesso in x = a se la funzione
f 0 è crescente in x = a. Il grafico di una funzione f è concavo in x = a se la
funzione f 0 è decrescente in x = a. Ogni punto in cui il grafico cambia concavità
è detto punto di flesso del grafico.
I grafici di f ed f 0 a pag. 115 illustrano quanto detto.
Concavità. A sinistra del punto B, il grafico di f è concavo; a sinistra di
B 0 il grafico di f 0 è decrescente.
Convessità. A destra del punto B, il grafico di f è convesso; a destra di
B 0 il grafico di f 0 è crescente.
Punto di Flesso. B è un punto di flesso; f 0 ha un minimo in B 0 .
Trovare i Flessi dal Grafico di f ’.
La direzione della concavità del grafico dipende, come mostra la definizione,
dalla crescita o decrescita della funzione derivata f 0 . Si ha un punto di flesso
quando f 0 - cambia direzione - cioè quando f 0 ha un minimo o un massimo
locale.
Esempio 68 Discutere la concavità della funzione f (x) = sin x.
Soluzione. E’ un fatto che dimostreremo più avanti, che se f (x) = sin x
allora f 0 (x) = cos x. Il raffronto tra i grafici rende, comunque, la cosa plausibile.
I
Siete daccordo?
Le radici di f 0
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
-0.2
2
x
4
6
0
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
-0.8
-1
-1
Grafico di f (x) = sin x
Da notare:
sono dove devono essere?
2
x
4
Grafico di f (x) = cos x
6
122
CAPITOLO 3. LE DERIVATE
Punti stazionari: f ha punti stazionari (un punto di massimo locale ed
un punto di minimo locale) per x = π/2 e x = 3 π/2 - esattamente le radici di
f 0 -.
Crescente o decrescente ? f cresce negli intervalli (0, π/2) e (3 π/2, 2 π) ;
sugli stessi intervalli f 0 è positiva
Concavità. f è concava nell’intevallo(0, π) dove f 0 è decrescente, e convessa
in (π, 2 π) dove f 0 cresce. Nei fatti, questo esempio mostra tutte le possibili
combinazioni di comportamento crescente/decrescente e concavità.
Punti di Fesso. f ha un punto di flesso in ogni multiplo di π - precisamente
dove f 0 assume un minimo od un massimo locale.
Esaminiamo ancora.
Esempio 69 Quello che segue è il grafico della derivata di una funzione f.
-3
-2
-1
1
x
2
3
Grafico di f 0
Spiegare perché:
(a) L’equazione f (x) = 0 non può avere più di due soluzioni nell’intervallo
[−3, 3]
(b) L’equazione f (x) = 0 non può avere due radici nell’intervallo [0, 3] ;
(c) Supponiamo che sia f (0) = 1. Quante soluzioni ha l’equazione f (x) = 0
nell’intervallo [−3, 3] ?
Soluzione. Poiché f 0 è negativa nell’intervallo (−3, 0) e positiva nell’intervallo (0, 3) , f decresce in (−3, 0) e cresce in (0, 3) . Ne segue che f ha un
minimo locale per x = 0 e nessun altro punto stazionario. Quindi
1. (a) Il grafico di f ha la forma di una U, quindi può intersecare l’intervallo
[−3, 3] al più in due punti.
(b) Il grafico di f cresce nell’intervallo (0, 3), può quindi intersecare l’asse
delle al più una volta.
(c) Se f (0) = 1 non ci sono radici nell’intervallo [−3, 3] perché x = 0 è
un punto di minimo per f.
¥
3.2. LA GEOMETRIA DELLE DERIVATE.
3.2.1
123
Esercizi
1. Il grafico di una funzione f è mostrato qui sotto
5
4
3
1
-5
-4
-3
-2
-1
0
1
-1
2 x 3
4
5
-2
-3
Grafico di f
(a) Su quali intervalli f 0 è negativa?
(b) Su quali intervalli f 0 è crescente? Su quali decrescente?
(c) In quali punti f 0 raggiunge il suo massimo? Stimare il valore di f 0 .
(d) In quali punti f 0 raggiunge il suo minimo? Stimare il valore di f 0 .
(e) Provare a fare uno schizzo del grafico per f 0 .
2. Il grafico della derivata di una funzione g è disegnata qua sotto. Usa il
grafico di g 0 per rispondere a questioni riguardanti g.
2
1
2
4
x
6
8
10
0
-1
-2
-3
Grafico di g 0
(a) Dove sono i punti stazionari di g ?
(b) In quali punti g ha massimo locale ? E minimo locale ?
(c) Il grafico di g 0 ha massimo locale in x = 2.7 e minimo locale in
x = 6.5. Cosa dicono questi punti del grafico di g ?
(d) g è concava o convessa in x = 5 ? E ad x = 8 ? Giustificare la risposta.
(e) Supponiamo sia g (0) = 0. Provare a fare uno schizzo del grafico di
g.
124
CAPITOLO 3. LE DERIVATE
3. Il grafico di una funzione f è mostrato qui sotto
10
8
6
4
2
-4
-3
-2
-1
0
1
2x
3
4
-2
Grafico di f 0
(a) Quali sono i punti stazionari di f ?
(b) Quali sono i massimi ed i minimi locali ?
(c) f è concava o convessa in x = 1 ? Giustificare la risposta.
(d) Provare a fare due schizzo di grafico di funzioni che potrebbero
essere f.
4. Supponiamo che la derivata di una funzione f sia f 0 (x) = x + 3.
(a) Su quali intervalli, se ci sono, f è crescente?
(b) Per quali valori di x la funzione f ha un massimo locale? Un minimo
locale?
(c) Su quali intervalli, se esistono, la funzione è concava?
(d) Provare a fare uno schizzo del grafico di f.
5. Ripetere l’esercizio precedente per le seguenti funzioni. (Approssimare le
risposte a due decimali)
(a) f 0 (x) = (x − 2) (x + 4) ;
(b) f 0 (x) = (x − 2)2 (x + 4) ;
(c) f 0 (x) = (x + 1)2 (x − 2) ;
¡
¢
(d) f 0 (x) = x2 + 1 (x + 6) ;
¡
¢
(e) f 0 (x) = x2 − 9 (x + 3) ;
1
;
(f) f 0 (x) =
1 + x2
x−2
;
(g) f 0 (x) = 2
x +5
x+1
(h) f 0 (x) = √
;
x2 + 1
x2 + 2
;
(i) f 0 (x) = √
x2 + 1
2
(j) f 0 (x) = e−x ;
3.2. LA GEOMETRIA DELLE DERIVATE.
125
¢
¡
(k) f 0 (x) = 9 − x2 e−x/4 ;
¢
¡
(l) f 0 (x) = ln 1 + x2 .
6. I grafici di f, f 0 , g (che non è la derivata di f ) sono disegnati sotto. Chi
è chi? Perché?
14
12
10
8
6
4
2
0
-2
-4
-6
1
2
x
3
4
5
7. Disegnare i grafici di funzioni con le seguenti proprietà.
(a) f (x) > 0 per ogni x e f 0 (x) > 0 per ogni x.
(b) g (x) > 0 per ogni x e g 0 (x) < 0 per ogni x.
(c) Trovare una formula per f e per g.
8. Disegnare i grafici di funzioni con le seguenti proprietà.
(a) f (x) < 0 per ogni x e f 0 (x) > 0 per ogni x.
(b) g (x) < 0 per ogni x e g 0 (x) < 0 per ogni x.
(c) Trovare una formula per f e per g.
9. Il grafico della derivata di una funzione f è disegnato sotto.
-2
-1
1
x2
3
4
Grafico di f 0
(a) Nell’intervallo [−2, 4] , dove è crescente f ? Perché ?
(b) Qual’è il punto stazionario di f ? E’ un massimo, un minimo o cosa ?
(c) Provare a disegnare un possibile grafico per f.
10. Sia f (x) = exp (sin x) . Quanti zeri (radici) ha f 0 nell’intervallo [0, 2π] ?
Quali sono i loro valori ? Giustificare la risposta.
126
CAPITOLO 3. LE DERIVATE
11. Supponiamo di conoscere le seguenti informazioni sulla funzione f :
(i) f è positiva su [−7, 8] ;(ii) f è crescente su [−2, 3] ;(iii) f è decrescente
su (4, 10) ;
(iv) f 0 è decrescente su [−3, 6] ; (v) f 0 (4) = 0; (vi) f ha un flesso in x = 7.
(a) Spiegare perché f ha un estremo locale in x = 4. E’ un massimo
locale o un minimo locale?
(b) Dove è concava f ?
(c) Dove è non negativa (≥ 0) f’ ?
(d) Metti in ordine crescente di valore i numeri f (4) , f 0 (5) , f 0 (6) , e
f (7) .
(e) Prova a disegnare un grafico per una funzione con queste proprietà.
3.2. LA GEOMETRIA DELLE DERIVATE.
3.2.2
127
La Geometria delle Derivate di Ordine Superiore
La derivata di una “buona” funzione f è ancora una funzione f 0 . Supponendo
f 0 “buona” il passo successivo è naturale: differenziare ancora. Il risultato è
una funzione , che indicheremo con f 00 , chiamata la derivata seconda di f .
Come f 0 , f 00 ci da informazioni utili su f .
Per esempio: la derivata di una funzione ci dice come, e quanto velocemente,
la funzione data cresce o decresce. Quindi, se f 00 (a) > 0, sappiamo che f 0 è
crescente per x = a. Ne segue che f è convessa per x = a.
Che cosa ci dice f 00 di f . Concavità e convessità.
Il grafico di f è convesso o concavo per x = a se f 0 è crescente o decrescente
per x = a. Il precedente principio, applicato ad f 0 ci dice che
Se f 00 (a) > 0, allora f 0 è crescente per x = a. Se f 00 (a) < 0,
allora f 0 è decrescente per x = a.
questo porta ad un test utile per la concavità
Fatto. Il grafico di f è convesso quando f 00 > 0
e concavo quando f 00 < 0.
Nota. Questo fatto non ci dice niente quando f 00 (a) = 0. In questo caso,
come vedremo, f può essere conca, convessa, o niente di tutto ciò.
Esempio 70 Discutere la concavità della funzione f (x) = sin x usando la
derivata seconda.
Soluzione. Se f (x) = sin x, allora f 0 (x) = cos x e f 00 (x) = − sin x (Mostreremo questo fatto più avanti, per il momento assumiamolo). Disegniamo i
grafici di f e di f 00 sugli stessi assi
1
0
1
2
3
x
4
-1
Grafici di f e di f 00
5
6
7
128
CAPITOLO 3. LE DERIVATE
Si vede facilmente che f è convessa dove f 00 > 0 e concava dove f 00 < 0. ¥
Nota. abbiamo affermato in precedenza, basandosi solo sull’evidenza grafica, che se f (x) = sin x allora f 0 (x) = cos x. Abbiamo inoltre affermato che
se g (x) = cos x allora g 0 (x) = − sin x. Entrambe le affermazioni richiedono di
essere dimostrate.
Notiamo tuttavia che le due affermazioni sono sostanzialmente identiche. Poiché
il grafico di f (x) e di g (x) differiscono solo per una traslazione orizzontale, lo
stesso deve avvenire per le loro derivate.
Ricerca dei Punti di Flesso.
Una funzione f ha un punto di flesso dove cambia il segno di f 00 . Ne segue,
quindi, che per una ”buona” funzione
Ogni punto di flesso di f è una radice di f 00 , è cioè una soluzione
di f 00 (x) = 0.
Nel grafico del seno, per esempio, si ha un punto di flesso per ogni radice di
f 00 .
Attenzione. Fare ancora attenzione alla formulazione dell’affermazione.
f 00 (a) può essere zero anche se non ci sono flessi in x = a.
Il seguente esempio mostra perché: Se f 00 (a) = 0 il punto a è un punto
stazionario di f 0 ma non necessariamente un massimo o minimo locale.
Esempio 71 Consideriamo i seguenti grafici di f, f 0 e f 00 . Discutere la concavità e i punti di flesso di f.
4
10
2
0.5
-1
0
x
1
5
-2
-1
0
Grafico di f
x
1
-4
Grafico di f 0
-1
0
x
1
Grafico di f 00
Soluzione. Sebbene sia f 00 (0) = 0, il punto (0, 0) non è un punto di flesso
per f . Si ha invece che il grafico di f è convesso ovunque poiché f 0 è ovunque
crescente.
Notare inoltre che si ha f (0) = f 0 (0) = f 00 (0) = 0. Se più di una derivata
di una funzione vale zero in un punto x = a, il grafico di f appare “piatto”
Maggiore è il nu- nell’intorno di x = a. I
¥
mero di derivate
che si annullano
per x = a, più
“piatto” appare
l grafico.
3.2. LA GEOMETRIA DELLE DERIVATE.
129
Ricostruiamo il Percorso: Massimi, Minimi, Concavità e Derivate
Seconde.
Un punto stazionario sul grafico di f può essere un massimo locale, un minimo
locale o nessuno dei due. Se si può disegnare un grafico accurato, la situazione
appare chiara. Se no, la concavità ci aiuta a distinguere tra le varie alternative.
L’idea è semplice:
In un minimo locale il grafico è convesso.
In un massimo locale il grafico è concavo.
Le seguenti affermazioni sono conseguenze immediate di questi dati. Esse
sono note come test della derivata seconda.
Fatto. (Test della derivata seconda).
Supponiamo che si abbia f 0 (a) = 0
Se f 00 (a) > 0, allora f ha un minimo locale in x = a
Se f 00 (a) < 0, allora f ha un massimo locale in x = a
Se f 00 (a) = 0 può accadere di tutto:
In x = a, f può avere massimo o minimo locale oppure niente.
Il grafico di f può essere concavo o convesso, avere un punto di flesso,
o niente di tutto ciò.
Consideriamo anche le formule Torniamo al primo esempio del paragrafo
precedente, nel quale avevamo considerato f ed f 0 , unendo a queste anche f 00 e
considerando anche le formule algebriche che le definiscono
f (x) = x3 − x2 − 6x ; f 0 (x) = 3x2 − 2x − 6 ; f 00 (x) = 6x − 2
Ecco i tre grafici.
18
16
14
4
2
-2
-1
1
x 2
3
15
10
10
8
6
4
2
0
-2
5
-2
-8
Grafico di f
Grafico di f 0
-2
-1
0
1
x 2
3
-5
0
-2
-4
-6
-6
-1
1
x 2
3
-10
-15
Grafico di f 00
Combinando grafici e formule, possiamo migliorare e reinterpretare le osservazioni precedenti:
130
CAPITOLO 3. LE DERIVATE
Che cosa dicono le derivate. Sia il grafico che la formula algebrica di f 0
suggeriscono che quando x → ∞ allora f 0 (x) → ∞. Quindi, per x → ∞ si ha che
la pendenza del grafico di f è, (a) positiva e, (b) crescente. Equivalentemente,
il grafico di f (a) sale e, (b) sale sempre più velocemente.
Punti Stazionari. I grafico di f ha retta tangente orizzontale nei punti stazionari A e C. In accordo con la formula della derivata prima, i punti
stazionari si hanno tra i valori di x per i quali è
f 0 (x) = 3x2 − 2x − 6 = 0
√ ¢
¡
Le radici di f 0 si trovano facilmente e sono: x = 1 ± 19 /3. In forma
decimale, le radici sono x ≈ −1.1196 e x ≈ 1.7863
Quanti sono i punti stazionari? Il calcolo precedente mostra che f 0 ha
solo due radici. Quindi A e C sono gli unici punti stazionari di f .
Punti di flesso. Il punto di flesso B si ha quando f 0 assume il suo valore
minimo, apparentemente vicino al punto x = 0.3. Dove cade esattamente B ?
La formula di f 00 ci da la risposta. f 00 ha un’unica radice per x = 1/3, dove
f 00 (x) = 6x − 2 = 0
Come mostra il grafico, f 00 cambia segno in x = 1/3, così f cambia concavità
in quel punto e solo in quel punto.
Il seguente esempio mostra la varietà di risultati che si possono ottenere da
un attenta osservazione del comportamento delle derivate.
Esempio 72 Il grafico mostra la forma di f 0 , la derivata di una certa funzione
f (che non viene data)
6
4
2
0
-2
-4
-6
-8
-3
-2
-1
0x
1
2
3
4
(a) Stimare f 00 (−3) ;
(b) Dove f è concava o convessa ?
(c) Quali sono i punti di flesso di f ?
Soluzione. Osservando attentamente il grafico si ottengono tutte le risposte.
E’ fondamentale ricordarsi che siamo osservando f 0 , non f o f 00 .
3.2. LA GEOMETRIA DELLE DERIVATE.
131
1. (a) Per definizione, f 00 (−3) = (f 0 )0 (−3) , cioè il coefficiente angolare
della retta tangente a f 0 nel punto x = −3. Una osservazione attenta
mostra che esso vale circa 5.
(b) Poiché f 00 (−3) > 0, f è convessa per x = −3. Più in generale, f
è convessa ovunque sia f 00 > 0 cioè dove f 0 è crescente. Il disegno
mostra che ciò avviene negli intervalli −4 ≤ x ≤ −1 e 3 ≤ x ≤ 4.
Per la stessa ragione f è concava in −1 ≤ x ≤ 3.
(c) La funzione f ha un flesso dove cambia concavità. La risposta (b) ci
dice che ciò accade per x = −1 e per x = 3.
¥
132
3.2.3
CAPITOLO 3. LE DERIVATE
Esercizi
1. Il grafico di una funzione f è disegnato qui sotto
8
6
4
2
0
-2
-4
-6
-8
-4
-3
-2
-1
x0
1
2
3
4
5
Grafico di f
(a) Per quali valori di x (se esistono) f 00 (x) è negativa? Positiva? Zero?
(b) Ordina, in ordine crescente, i numeri f 0 (0) , f (2) , f 0 (2) , e f 00 (2) .
2. Dell’acqua fluisce, in modo costante in un cilindro a base circolare. Sia
V (t) il volume dell’acqua al tempo t, H (t) l’altezza dell’acqua al tempo
t . Dare una interpretazione fisica alle seguenti quantità ed indicare se
sono positive, negative o nulle:
(a) V 0 (t) ,
(b) H 0 (t) ,
(c) V 00 (t) ,
(d) H 00 (t) .
3. Il grafico di f è dato da: [Nota: f ha punti di flesso in x = 0.7 e x = 2.6
]
6
5
4
3
2
1
0
0.5
1
1.5
x
2
2.5
3
(a) In quali intervalli f 00 è positiva? Negativa? Nulla?
(b) Ordina, in ordine crescente, i numeri f (0) , f 00 (0.5) , f 00 (2) , f 00 (2),
e f 00 (2.8) .
3.2. LA GEOMETRIA DELLE DERIVATE.
133
4. Il grafico della derivata seconda di una funzione g è disegnato sotto. Usa
il grafico per rispondere alle seguenti domande su g 0 e g.
3
2
1
1
x2
3
4
0
-1
-2
-3
-4
-5
-6
-7
-8
-9
Grafico di g 00
(a) Dove è convessa g ?
(b) Quali sono i punti di flesso di g ?
(c) Ordina, in ordine crescente, i numeri g 0 (0) , g 0 (1) , g 0 (2) , g 0 (3) .
(d) Supponiamo che g 0 (0) = −4 g è crescente o decrescente in x = 2 ?
Giustifica la risposta.
(e) Supponiamo che g 0 (0) = 0 g è crescente o decrescente in x = 2 ?
Giustifica la risposta.
(f) Supponiamo che g 0 (0) = 0 g è crescente o decrescente in x = 2 ?
Giustifica la risposta.
5. Nella prima colonna sono disegnati i grafici di quattro funzioni. Nella
seconda, in ordine diverso, quello delle loro derivate seconde. Individuare
funzioni e relative derivate seconde [Nota: le scale degli assi possono non
134
CAPITOLO 3. LE DERIVATE
essere le stesse]
x
x
x
x
x
x
x
x
6. I grafici di f, f 0 , f 00 sono disegnati sotto. Determinare chi è chi, e spiega
come hai fatto a decidere.
3
2
1
-2
-1
0
1x
2
-1
7. I grafici di f, f 0 , f 00 sono disegnati sotto. Determinare chi è chi, e spiega
3.2. LA GEOMETRIA DELLE DERIVATE.
135
come hai fatto a decidere.
1
0.8
0.6
0.4
0.2
0
-0.2
1
2
x
3
4
5
-0.4
-0.6
8. Supponiamo che f, f 0 , f 00 siano funzioni continue su (−∞, +∞) e che f
abbia le seguenti proprietà:
(i) f è negativa nell’intervallo (−10, 1) e positiva su (3, 10) ;
(ii) f è crescente nell’intervallo (−∞, 5) e decrescente su (5, +∞) ;
(iii) f è convessa in (−∞, 2)e concava in (2, +∞) .
Scrivere in ordine crescente di valore i seguenti numeri: f 0 (0) , f 0 (1) , f 0 (2) ,
f 00 (2) e f 0 (8)
9. Ripetere il Problema 2, supponendo che il serbatoio sia una sfera.
10. Ripetere il Problema 2, supponendo che il serbatoio sia un cono col vertice
in basso.
11. Supponiamo che f, f 0 , f 00 siano funzioni continue su R.
(a) Disegnare un grafico di f nel caso che f (x) > 0, f 0 (x) > 0, f 00 (x) >
0;
(b) Disegnare un grafico di f nel caso che f (x) > 0, f 0 (x) < 0, f 00 (x) >
0;
(c) Disegnare un grafico di f nel caso che f (x) < 0, f 0 (x) < 0, f 00 (x) <
0;
(d) Disegnare un grafico di f nel caso che f (x) < 0, f 0 (x) > 0, f 00 (x) <
0.
12. Dire se esiste una funzione definita su R tale che f (x) > 0, f 0 (x) <
0, f 00 (x) < 0. Se si disegnarla; se no spiegare il perché.
13. Dire se esiste una funzione definita su R tale che f (x) < 0, f 00 (x) > 0.
Se sì disegnarla; se no spiegare il perché.
14. Disegnare il grafico di una funzione g che possegga tutte le seguenti proprietà.
(i) Il dominio di g è l’intervallo [−3, 5] ;
(ii) g 00 (x) < 0 per tutti gli x ∈ (−2, 1) ;
(iii) g 00 (x) < 0 per tutti gli x ∈ (1, 2) ;
136
CAPITOLO 3. LE DERIVATE
(iv) g 0 (−2) < 0;
(v) g (1) = 0 ma g (1) non è né massimo né minimo di g nell’intervallo
[−2, 4] .
15. Disegnare il grafico di una funzione continua h che possegga tutte le
seguenti proprietà.
(i) h0 (x) < 0 per tutti gli x 6= 4;
(ii) h0 (4) non esiste;
(iii) h00 (x) < 0 per tutti gli x < 4;
(iv) h00 (x) > 0 per tutti gli x > 4.
16. Supponiamo sia 1 ≤ f 00 (x) ≤ 3 per 2 ≤ x ≤ 4. Supponiamo inoltre che
f 0 (2) = 5 e che f (2) = −6.
(a) Spiegare perché f 0 (3) ≤ 8;
(b) Usare (a) per mostrare che f (3) ≤ 2;
(c) Spiegare perché f 0 (3) ≥ 6;
(d) Trovare una limitazione superiore ed una inferiore per f 0 (4) ;
(e) Trovare una limitazione superiore ed una inferiore per f (4) .
17. Supponiamo che f, f 0 , f 00 siano funzioni continue su R, che f 0 (2) = −1
e che 0.1 < f 00 (x) < 0.5 per 2 < x < 4. Trovare una limitazione superiore
ed una inferiore per il valore di f 0 (3) . [Sugg.: Applicare il principio delle
corse].
18. Supponiamo che la retta y = 2x − 1 sia tangente al grafico di f nel punto
x = 3 e che f 00 (x) > 0 per 0 < x < 5.
(a) Trovare f 0 (3) e f 00 (3) ;
(b) Spiegare perché è vero che 7 < f (4) ;
(c) Trovare una limitazione inferiore per il valore di f (2) .
19. Supponiamo sia f (2) = 5, f 0 (2) = 2 e che la funzione f sia convessa
ovunque.
(a) Quante radici potrebbe avere f ? Cosa si può dire della loro localizzazione?
(b) Trovare una limitazione inferiore per il valore di f (0) ;
(c) Supponiamo sia f (−2) = −1. Mostrare che f (0) < 3.
20. Dire se la seguente affermazione è vera o falsa. Giustificare la risposta.
Se f (2) = 3, f 0 (2) = 1 e f 00 (2) = 0 allora
il grafico di f (x) ha un flesso nel punto (2, 3) .
21. Supponiamo che sia f 0 (c) = f 00 (c) = 0 ma f 000 (c) > 0. Dire se f ha in
x = c un punto di massimo relativo, minimo relativo o flesso. Spiegare il
perché.
3.3. DEFINIZIONE DI DERIVATA
3.3
137
Variazione Media ed Istantanea: Definizione di
Derivata
In questo paragrafo, affronteremo le derivate da un punto di vista più formale.
Data una funzione f ed un valore dell’ingresso x = a, cercheremo di spiegare che
cosa significa esattamente il simbolo f 0 (a). Fino ad ora abbiamo interpretato
il simbolo f 0 (a) come la pendenza della retta tangente al grafico di f nel punto
x = a o come il tasso di variazione istantanea di f relativamente al punto
x = a, ma rimangono aperte questioni importanti quali, ad esempio: che cosa
significa esattamente l’espressione “variazione istantanea” di una funzione in un
punto? Come è definita esattamente la retta tangente al grafico di una curva?
E, più importante di tutte, come è possibile usare la formula che definisce f
per calcolare - non solo stimare - i valori di f 0 ? Osserviamo ancora una volta,
i problemi che vogliamo affrontare tramite un paio di esempi.
3.3.1
Il Problema della Variazione.
Esempio 73 A mezzanotte esatta, il Professor X parte sulla sua vecchia Cinquecento. L’odometro segna zero e d il quadrante delle velocità è rotto. Consultando
l’odometro e l’orologio da polso il Professor X può, ad ogni istante t (misurato
in ore), conoscere la distanza totale percorsa D (t) (in chilometri). Egli può
anche disegnare il grafico di D (t)
180
160
140
120
100
km
80
60
40
20
0
0.5
1
1.5
ore
2
2.5
3
Grafico di D (t)
Come può il Professor X calcolare la sua velocità al tempo t = 2 ?
Soluzione. La lettura dell’odometro per t = 2 non aiuta. Essa può dire
che egli ha percorso 100 km in 2 ore e quindi che la sua velocità media è di
50 km/h, ma qual’è la sua velocità all’istante t = 2 ?
Il Professor X può ragionare che calcolare la velocità media su di un intervallo
di tempo più breve, per esempio nell’intervallo che va da t = 1.99 a t = 2 può
138
CAPITOLO 3. LE DERIVATE
dare una risposta migliore. L’odometro riporta che nell’intervallo dato sono
state percorsi 0.6714 km, quindi la velocità media in quel periodo di tempo è
0.7985 km
= 79.85 km/h
0.01 ore
ma questo valore non è ancora quello della velocità all’istante t = 2.
¥
Riprendiamo il problema della retta tangente ad una curva. La domanda
che esso pone è la seguente
Data una curva C ed un punto P su C, descrivere
l’equazione della retta tangente a C in P.
Esempio 74 Qual’è l’equazione della retta tangente al grafico di f (x) = x2 +x
nel punto x = 2 ?
Soluzione. Disegniamo il grafico della curva, con una tangente plausibile
nel punto (2, 6)
12
10
8
6
4
2
0
-2
0.5
1
1.5
x
2
2.5
3
-4
Grafico di x2 + x e retta tangente in (2, 6)
Dal solo grafico, come fatto in precedenza, si può stimare che il coefficiente
Controlla l’affer- angolare m della retta tangente R sia 5 I. Se questo è vero, l’equazione della
mazione
retta è y = 5 (x − 2) + 6.
Trovare il coefficiente angolare di R esattamente non è banale poiché conosciamo un solo punto per cui passa la retta. Per cominciare, consideriamo
l’equazione della retta R0 che passa per due punti vicini del grafico, per esempio
x = 2 e x = 2.01. Ci aspettiamo che R ed R0 abbiano coefficienti angolari simili.
Conoscendo due punti di R0 è possibile calcolare il coefficiente angolare m0 della
retta. Si ha
m=
f (2.01) − f (2)
6.0501 − 6
∆f
=
=
= 5.01
∆x
2.01 − 2
0.1
3.3. DEFINIZIONE DI DERIVATA
139
¥
L’evidenza numerica conferma la nostra valutazione che m = 5.
Il problema della retta tangente è ancora stato posto in termini intuitivi, ma
vaghi. Dobbiamo ancora chiarire che significa l’espressione “data una curva” e
come si “descrive” la retta tangente a C in P.
Dare un equazione. Spesso le curve sono descritte da equazioni (per esempio x2 + y2 = 9) o da funzioni (esempio f (x) = x2 + x). Altre volte sono
descritte solo graficamente o numericamente, senza una formula algebrica che
le sostanzi. In quest’ultimo caso la retta tangente può essere determinata solo
in modo approssimato. Se la curva C è descritta con una formula vorremmo
essere capaci di trovare una formula esatta per l’equazione della retta tangente
a C in P.
Ricerca di m. Una retta R è completamente determinata dal suo coefficiente angolare m e dal passaggio per un punto P. Nel problema della retta
tangente, il punto P è dato, rimane da determinare m. Determinare la retta
tangente significa quindi determinare m.
Non esiste retta tangente. Non tutte le curve ammettono retta tangente
in un dato punto P . Per esempio, il grafico di y = |x| ha uno spigolo in
P = (0, 0) e quindi non ammette retta tangente in quel punto.
Esempio 75 Abbiamo valutato che la retta y = 5 (x − 2) + 6 sia tangente a
C, grafico di f (x) = x2 + x nel punto x = 2. Controllare il risultato con
il metodo grafico dell’ingrandimento.
Soluzione. Ecco i grafici di C e di R in quattro scale diverse
12
40
10
30
8
20
6
10
4
-1
0
1
2
3x
4
5
6
2
-10
1
1.5
2x
2.5
3
140
CAPITOLO 3. LE DERIVATE
6.4
8
7
6.2
6
6
5
5.8
4
5.6
1.6
1.8
2x
2.2
2.4
1.9
1.95
2x
2.05
2.1
I grafici mostrano che C vista più da vicino, si confonde con R, come affermato. In particolare, poiché R ha coefficiente angolare 5 anche la curva C lo
ha nel punto (2, 6) .
¥
I metodi grafici (ingrandimento grafico, traccia della retta a mano, e così
via) danno semplicemente una stima utile; per capire meglio e più chiaramente
il significato di derivata abbiamo bisogno di una definizione concisa, chiara,
espressa in linguaggio matematico. Il concetto che dobbiamo introdurre per
questo scopo è quello di limite.
Cercheremo di risolvere due problemi in parallelo.
Il Problema della Retta Tangente. Sia f (x) una funzione. Trovare il
coefficiente angolare della retta tangente al grafico di f nel punto x = x0 .
Il Problema della Velocità Istantanea. Sia s = D (t) la funzione distanza, percorsa per esempio da un’ automobile, come funzione del tempo t.
Trovate la velocità istantanea al tempo t = t0 .
Rette Secanti, Tangenti e Limiti.
Dati due punti P e Q su di una curva C, si può tracciare la retta secante
passante per P e Q. Se P e Q sono abbastanza vicini tra di loro è ragionevole
aspettarsi che la retta secante, che essi determinano, sia molto “vicina” alla
retta tangente a C in P.
Se determinare il coefficiente angolare di una retta tangente è un problema
non banale, la determinazione del coefficiente angolare di una retta secante è
semplice. Se C è il grafico di f (x) e P = (a, f (a)) e Q = (b, f (b)) sono i punti
su C, allora, come mostra il grafico
si ha che il coefficiente angolare della secante da P a Q è dato da
m=
f (b) − f (a)
∆f
=
.
∆x
b−a
3.3. DEFINIZIONE DI DERIVATA
141
Figura 3.3:
In precedenza avevamo calcolato che la secante alla curva data da f (x) =
+ x nei punti x = 2 e x = 2.01 aveva m = 5.01. Il risultato suggerisce
la strategia da seguire. Porteremo la pendenza della secante a quella della
tangente, diminuendo sempre più l’ampiezza degli intervalli.
x2
Che cosa E’ un Limite ? Il limite è uno strumento matematico usato per
descrivere il comportamento di una funzione f (x) per valori di x vicini ad un
valore assegnato x = a. Nei prossimi due paragrafi tratteremo in modo formale
questo concetto. Adesso ci limitiamo a farlo in modo informale, nel contesto
degli esempi citati.
Esempio 76 Calcolare il valore del coefficiente angolare m per rette secanti il
grafico di f (x) = x2 + x su piccoli intervalli intorno ad x = 2. Interpretare i
risultati nel linguaggio dei limiti. Concludere, decidendo il valore di f 0 (2) .
Soluzione. Riportiamo di seguito i risultati relativi a vari intervalli
Coefficienti angolari m delle secanti su piccoli intervalli
Intervallo [1.99, 2] [1.999, 2] [2, 2.001] [2, 2.01] [2, 2.1]
m
4.99
4.999
5.001
5.01
5.1
Per rileggere la situazione nel linguaggio dei limiti, consideriamo un intervallo che va da x = 2 a x = 2 + h I. Allora, la secante da x = 2 a x = 2 + h Pensare ad h
come un piccolo
ha coefficiente angolare
∆f
f (2 + h) − f (2)
f (2 + h) − f (2)
m=
=
=
∆x
(2 + h) − 2
h
Il coefficiente della retta tangente a x = 2 è il valore limite che si ottiene
quando si manda h a zero nella frazione; in simboli
incremento
(positivo
negativo).
o
142
CAPITOLO 3. LE DERIVATE
f 0 (2) = lim
h→0
f (2 + h) − f (2)
h
Usciamo dalla teoria cercando di calcolare ciò che abbiamo scritto
f (2 + h) − f (2)
h→0
h
lim
(2 + h)2 + (2 + h) − 6
h→0
h
2
5h + h
= lim (5 + h)
= lim
h→0
h→0
h
= 5
=
lim
¥
(Il calcolo del precedente limite dovrebbe essere intuitivamente ragionevole.
Studieremo più avanti l’algebra dei limiti).
Velocità Media, Velocità Istantanea e Limiti.
Per il Professor X, il problema del tasso di variazione è quello di convertire le
informazioni sulla distanza, in informazioni sulla velocità. La soluzione di tale
problema è molto simile a quella operata per il problema delle tangenti.
La velocità media su di un intervallo di tempo è molto facile da calcolare.
Come tutti sappiamo
velocità media =
distanza percorsa
.
tempo trascorso
Il problema che rimane è quello di collegare la velocità media (su di un intervallo) con la velocità istantanea. Ancora una volta, il concetto di limite ci da
lo strumento adatto. La velocità istantanea al tempo t0 è il limite della velocità
media su intervalli sempre più piccoli che contengono t0 . Più succintamente:
Consideriamo l’intervallo di tempo tra t = 2 e t = 2 + h. La velocità media
su tale intervallo è data da
∆D
D (2 + h) − D (2)
D (2 + h) − D (2)
=
=
∆t
(2 + h) − 2
h
Quindi la velocità istantanea al tempo t = 2 è
D (2 + h) − D (2)
h→0
h
lim
Supponendo, per esempio, che la formula della distanza possa essere D (t) =
20t + 15t2 avremmo il seguente calcolo
lim
h→0
D (2 + h) − D (2)
h
20 (2 + h) + 15 (2 + h)2 − 100
h→0
h
15h2 + 80h
= lim 15h + 80
= lim
h→0
h→0
h
= 80 .
=
lim
Quindi, alle 2.00 esatte, il Professor X andava esattamente a 80 km/h.
3.3. DEFINIZIONE DI DERIVATA
3.3.2
143
Derivata: Definizione Formale.
Il problema della tangente e quello della velocità istantanea hanno rivelato di
essere identici. Entrambi i problemi, così come molti altri, portano ad un limite
della stessa forma. La forma appare nella seguente definizione.
Definizione 77 Sia f una funzione definita in x = a ed in un suo intorno. La
derivata di f per x = a , indicata con f 0 (a) ,è definita dal limite
lim
h→0
f (x + h) − f (x)
h
Questa importantissima definizione richiede alcuni chiarimenti:
f 0 (a) deve esistere? Risposta: NO. Il limite nella definizione può o
meno esistere. Se esiste, diremo che f è differenziabile per x = a o che f
ammette derivata per x = a. Molte delle funzioni che considereremo nel corso
sono derivabili nel loro dominio. L’eccezione principale è la funzione f (x) = |x| .
Lo spigolo che essa ha in x = 0 implica che essa non può avere tangente in quel
punto e quindi non è derivabile per x = 0 (vedremo il calcolo esplicito nel
prossimo paragrafo).
Dividere per zero? Il limite nella definizione di derivata implica sempre
che il denominatore tenda a zero; il calcolo del limite implica sempre l’uso di un
qualche “trucco” . In pratica, dopo un po’ d’algebra sul numeratore, dovremmo
poter essere in grado di semplificare e liberarci della quantità h al denominatore
che ci dà problemi di divisione per zero.
Altre forme.
Il limite nella definizione di derivata può essere scritto in
altre forme equivalenti. Ecco le più usate:
f (a + h) − f (a)
h
f (x) − f (a)
limx→a
x−a
limh→0
f (a + ∆x) − f (a)
∆x
∆f
lim∆x→0
∆x
lim∆x→0
A secondo della forma di f può essere più semplice o più facile usarne una
o l’altra, ma tutte contengono la stessa informazione e conducono allo stesso
risultato.
Rapporto Incrementale.
I quozienti nei limiti precedenti sono tutte riformulazioni della stessa idea:
Definizione 78 Per ogni funzione f, il rapporto
f (a + h) − f (a)
h
è chiamato rapporto incrementale. Esso misura il tasso di variazione media
della funzione f dal punto x = a al punto x = a + h.
144
CAPITOLO 3. LE DERIVATE
Per capire meglio ciò che afferma, consideriamo separatamente le sue varie
componenti:
Il denominatore. La differenza h = (a + h) − a = ∆x rappresenta
il tasso di variazione, o incremento, della variabile di ingresso, da x = a a
x = a + h (il cambiamento può essere sia positivo che negativo).
Il Numeratore. Quando x varia dal valore a al valore a + h , l’uscita
f (x) varia anch’essa. Il numeratore ∆f = f (a + h) − f (a) misura questo
cambiamento. Così come ∆x, ∆f può avere un segno positivo o negativo.
Il Quoziente. Il quoziente misura il rapporto tra queste variazioni e rappresenta quindi la velocità di cambiamento di f rispetto ad x. Poiché il tasso di
variazione avviene rispetto ad un intervallo in x , esso rappresenta una variazione media. Il segno di ∆f /∆x ci dice se x e f (x) cambiano nella stessa
direzione. Se, per esempio, ∆f / ∆x < 0, un incremento positivo in x produce
una variazione negativa in f (x) .
Dalla Media all’Istantaneo. Il rapporto incrementale rappresenta il tasso
di variazione media sull’intervallo [a, a + h] . Il limite
lim
h→0
f (a + h) − f (a)
h
è il tasso di variazione istantanea all’istante x = a.
Rapporti Incrementali e Derivate: Loro Significato in Diverse Situazioni. Ogni funzione f ha diverse possibili interpretazioni. Per esempio la
funzione f (x) = x2 + x , che abbiamo già usato, può rappresentare il peso di un
neonato x giorni dopo la nascita, l’area di un rettangolo di lati variabili, la distanza percorsa al variare del tempo, o qualsiasi altra cosa. Ogni interpretazione
di f porta ad un significato diverso del rapporto incrementale. Eccone alcuni
esempi. In ogni situazione, il rapporto incrementale e la derivata rappresentano
variazioni di quantità. Fate attenzione, in particolare, alle unità di misura. La
scelta delle unità di misura per x e per f (x) determinano l’unità di misura del
rapporto incrementale e della derivata.
Pendenza. Su ogni grafico del tipo y = f (x) il rapporto incrementale rappresenta il coefficiente angolare della retta secante passante per i punti (a, f (a))
e (a + h, f (a + h)) . La derivata rappresenta il coefficiente angolare della retta
tangente in x = a.
Velocità. Se y = f (x) rappresenta la posizione di un oggetto che si muove
al tempo x, allora il rapporto incrementale rappresenta la velocità media nell’intervallo che va da x = a a x = a + h. La derivata f 0 (a) rappresenta la
velocità istantanea al tempo x = a.
Consumo di Benzina. Supponiamo che y = g (x) rappresenti la distanza
totale percorsa (in km) dal Professor X con x litri di carburante. In tal caso,
per esempio, il rapporto incrementale
g (2) − g (0)
2
misura il consumo medio nell’intervallo nel quale sono stati consumati i primi
due litri di carburante. Il consumo istantaneo cambia da momento a momento.
3.3. DEFINIZIONE DI DERIVATA
145
Per trovare il consumo, per esempio, per x = 2 bisogna trovare il limite. Senza
una formula esplicita per la funzione, essa non può essere calcolata.
Unità di Misura. Quali sono le unità di misura per il rapporto incrementale e la derivata? Dipende, ovviamente dalle unità di misura usate per x e
per f (x) . Nel caso del Professor X, la distanza era misurata in chilometri, il
tempo in ore quindi l’unità di misura del quoziente è di chilometri/ora per la
velocità e, nel caso del consumo di carburante di chilometri/litro.
146
3.3.3
CAPITOLO 3. LE DERIVATE
Esercizi
1. Luciana viaggia da Torino a Genova. A causa di lavori sulla strada ella
guida i primi 20 km a velocità costante di 40 km/h, Quindi, per i successivi
70 km,a velocità costante di 100 km/h. Si ferma poi in un’area di servizio
per 200 per un caffè e guida gli ultimi 50 km alla velocità costante di
80 km/h.
(a) Disegnare il grafico della distanza percorsa da Luciana come funzione
del tempo.
(b) Disegnare il grafico della velocità Luciana come funzione del tempo.
(c) Qual’è la velocità media di Luciana su tutto il viaggio?
2. Se f (1) = 2 e il tasso di variazione media di f da x = 1 ad x = 5 è 3 ,
quanto vale f (5) ?
3. Se f (2) = 1 e il tasso di variazione media di f da x = −3 ad x = 2 è 4 ,
quanto vale f (−3) ?
4. Vero o falso? Giustificare la risposta.
(a) La velocità è il tasso di variazione della posizione nel tempo.
(b) Se il tasso di variazione media di una funzione in un intervallo di
tempo è zero, allora la funzione è costante.
(c) Se il tasso di variazione media di una funzione su ogni intervallo di
tempo è 15 allora il grafico di una funzione è una retta.
5. La posizione p (t) di un oggetto (misurata in metri), al variare del tempo
(misurato in secondi) è data da p (t) = 3t2 + 1.
(a) Trovare di quanto è variata la posizione dell’oggetto nell’intervallo
di tempo tra t = 1 e t = 3.
(b) Trovare la velocità media dell’oggetto nell’intervallo di tempo tra
t = 1 e t = 3.
(c) Disegnare il grafico di g (t) quello della retta secante tra t = 1 e
t = 3. Trovare l’equazione della secante.
(d) Trovare la velocità media dell’oggetto nell’intervallo di tempo tra
t = 1 e t = 1 + h. Quale sono le unità di misura della risposta?
(e) Trovare la velocità istantanea per t = 1.
(f) Scrivere l’equazione della retta tangente al grafico per t = 1. Aggiungere questa retta al grafico del punto (c).
6. Per ognuna delle funzioni f sotto, usa il rapporto incrementale con h =
0.01 per stimare il valore di f 0 nel punto assegnato.
(a) f (x) = x2 − 3x nel punto x = 3;
3.3. DEFINIZIONE DI DERIVATA
147
(b) f (x) = x1/3 nel punto x = 2;
(c) f (x) = x−2 nel punto x = 1;
(d) f (x) = sin x nel punto x = 0;
(e) f (x) = cos x nel punto x = 0;
(f) f (x) = cos 3x nel punto x = π/2;
(g) f (x) = 2x nel punto x = 0;
(h) f (x) = ln x nel punto x = 1.
f (1 + ∆x) − f (1)
∆x
disegnato su un piccolo intervallo centrato in ∆x = 0 per stimare f 0 (1) .
7. Per ognuna delle funzioni sotto, usa il grafico di g (∆x) =
(a) f (x) = x3 ;
(b) f (x) = x + 1/x;
(c) f (x) = sin (πx) ;
(d) f (x) = ex .
√
8. Sia f (x) = x. Costruire una tabella con i valori di f nei punti x =
1.998, 1.999, 2.000, 2.001 e 2.002. Usare i risultati per rispondere alle
seguenti domande (arrotondare i valori di f (x) alla settima cifra decimale).
(a) Stimare i valori di f 0 (1.999) , f 0 (2) , f 0 (2.001) usando i valori tabulati di f ;
(b) Il rapporto (f (2.001) − f (2)) /0.001 sottostima o sovrastima il valore di f 0 (2)? Perché?
(c) Stimare f 00 (2) usando il risultato in (b).
9. Ripetere il problema precedente per le seguenti funzioni:
(a) f (x) = x2 ;
(b) f (x) = sin x;
(c) f (x) = |x| ;
(d) f (x) = ex ;
(e) f (x) = ln x.
10. Sia f (x) = |x| .
(a) Disegnare il grafico di f nell’intervallo [−3, 3] .
½
−1 se x < 0
0
.
(b) Spiegare perché si ha f (x) =
1 se x > 0
(c) Spiegare perché non esiste f 0 (0) .
11. Sia f (x) = x2 .
148
CAPITOLO 3. LE DERIVATE
(a) Trovare il tasso di variazione media di f tra x = 0 e x = 0.01. Usare
il risultato per stimare f 0 (0) . Spiegare perché la stima è per eccesso.
(b) Trovare il tasso di variazione media di f tra x = −0.01 e x = 0.
Usare il risultato per stimare f 0 (0) . Spiegare perché la stima è per
difetto.
(c) Trovare il tasso di variazione media di f tra x = −0.01 e x = 0.01.
Usare il risultato per stimare f 0 (0) .
(d) Come mai la stima in (c) è più accurata di quella in (a) o in (b) ?
(e) Partendo da (c), descrivere un metodo per stimare f 0 (a) partendo
da i dati tabulati.
12. Ognuno dei seguenti limiti è f 0 (a) per qualche funzione f e qualche
numero x = a. Identificare f ed a.
√
x−2
;
(a) limx→4
x−4
52+h − 25
;
(b) limh→0
h
√
cos u − 2/2
;
(c) limu→π/4
x − π/4
log2 s − 3
.
(d) lims→8
s−8
3.4. LIMITI E CONTINUITÀ.
3.4
149
Limiti e Continuità.
Nel precedente paragrafo abbiamo introdotto il concetto di limite in funzione
della definizione di derivata. Vogliamo adesso studiare più in dettaglio il concetto di limite ed usarlo per definire un’altra importante concetto: la continuità
di una funzione in un punto del dominio.
3.4.1
L’Idea Base: Alcuni Esempi Semplici.
L’idea generale di limite è abbastanza semplice. Supponiamo che f sia una
funzione definita in un intorno del punto x = a, anche se non necessariamente
punto x = a. Affermare che
lim f (x) = L
x→a
significa, informalmente, che i valori di f (x) si avvicinano al valore L quando
x si avvicina al valore a. Usando altri simboli potremmo scrivere che
f (x) → L quando x → a
Con altre parole:
Quando la variabile d’ingresso x tende al valore a, il valore dell’uscita f (x)
tende al valore L.
Ancora, in altri termini,
f (x) ≈ L quando x ≈ a.
Osserviamo subito che le idee intuitive se servono, e servono, a capire un
concetto, un’idea, non sono definizioni formali, che daremo presto.
Cominciamo, come al solito, con alcuni esempi.
Esempio 79 Quanto vale limx→3 x2 ? Perché ?
Soluzione. La risposta non genera alcuna sorpresa. E’ ovviamente,
lim x2 = 9.
x→3
La funzione quadrato si “comporta bene” nell’intorno del punto x = 3. In
particolare f (x) ≈ 9 quando x ≈ 3. (Notare che il fatto che sia f (3) = 9 è
irrilevante nel calcolo del limite).
¥
Esempio 80 L’affermazione
x2 − 9
=6
x→3 x − 3
lim
riguarda il limite di una certa funzione in un certo punto. Quale funzione?
Quale punto? Che cosa dice l’affermazione? E’ vero o falso?
150
CAPITOLO 3. LE DERIVATE
Soluzione.¡ La funzione,
che indicheremo con la lettera g, è definita dalla
¢
2
regola g (x) = x − 9 / (x − 3) . Il punto in questione è il punto x = 3.
Da notare che la funzione g non è definita nel punto x = 3 (mentre in ogni
altro punto la regola che definisce la funzione è definita). Il limite, così come
scritto, afferma che, sebbene g non sia definita nel punto x = 3, i valori di g (x)
tendono al valore 6 quando l’ingresso x tende al valore 3. In simboli
g (x) → 6 quando x → 3.
Questo è precisamente ciò che afferma il limite che abbiamo scritto. L’affermazione è vera?
La formula di g non è di aiuto immediato poiché la funzione non è definita per
x = 3. Il grafico di g è di maggior aiuto
9
8
7
6
5
4
3
2
1
0
1
2
3x
4
5
6
x2 − 9
Grafico di g (x) =
x−3
Esso mostra, in maniera convincente, che l’affermazione del limite è vera.
Nonostante che la formula presenti un problema di divisione per zero in x = 3,
la funzione g (x) tende ad assumere il valore 6 quando x tende verso il valore 3,
sia da destra che da sinistra.
Osserviamo infine, che il grafico di g assomiglia in modo inequivocabile a quello
della retta y = x + 3. L’algebra ci spiega, in modo elementare, il motivo: Se
x 6= 3 si ha
g (x) =
(x − 3) (x + 3)
x2 − 9
=
=x+3
x−3
(x − 3)
Ripeto: l’ultima uguaglianza vale solo per x 6= 3, ma ciò è sufficiente poiché
siamo interessati solo a g (x) per valori di x diversi da x = 3. Una volta eseguita
la semplificazione algebrica è chiaro che
lim g (x) = lim (x + 3) = 6.
x→3
x→3
¥
Perché i Limiti Interessano.
Le espressioni più semplici quali limx→3 x2 = 9 oppure limx→3 (x + 3) = 6
illustrano che cosa intendiamo per limite, ma non ci dicono perché siamo interessati a questa nuova operazione. A giudicare dagli esempi precedenti i limiti
3.4. LIMITI E CONTINUITÀ.
151
sembrano essere una complicazione senza contropartite. Questa impressione è
errata. I limiti sono uno dei concetti fondamentali dell’Analisi. Una prima
ragione è che funzioni con problemi nel loro dominio, come quella dell’Esempio precedente, si incontrano spesso in Analisi. Una seconda ragione sta nella
definizione di derivata di una funzione.
Esempio 81 Sia f (x) = x2 . Usarel a definizione per calcolare il valore della
derivata f 0 (3) . Che cosa significa il risultato graficamente?
Soluzione. Per definizione la derivata di f nel punto x = 3 è il limite del
rapporto incrementale nel punto 3. Si ha perciò
f (x) − f (3)
x2 − 9
= lim
.
x→3
x→3 x − 3
x−3
f 0 (3) = lim
Sappiamo, dall’esempio precedente, che tale limite vale 6, quindi f 0 (3) = 6. In
termini grafici si ha che in x = 3 la retta tangente al grafico della funzione f ,
ha coefficiente angolare 6.
¥
Limiti in Pratica.
Molti dei limiti che incontreremo saranno semplici e diretti da calcolare.
Mettendo insieme le risorse algebriche, geometriche, grafiche e numeriche a
nostra disposizione, riusciremo a dare una risposta semplice e convincente anche
a quei limiti che a prima vista possono sembrare “impossibili”.
Esempio 82 Sia f (x) = sin x. Quale limite definisce f 0 (0) ?.Che cosa significa
il limite geometricamente? Calcolare il limite.
Soluzione. La derivata f 0 (0) è il coefficiente angolare della retta tangente
al grafico della curva y = sin x nel punto x = 0. Il valore della derivata della
funzione in x = 0 è dato dal limite del rapporto incrementale della funzione,
relativamente al punto x = 0, cioè
f 0 (0) = lim
x→0
sin x − sin 0
sin x
= lim
x→0 x
x−0
Cerchiamo di capire il risultato di questo limite valutando il rapporto sin x/x
nell’intorno dello 0. Ecco di seguito alcuni risultati numerici, arrotondati alla
quinta cifra decimale.
x
sin x/x
−0.1
0.99833
−0.01
0.99998
−0.0001
1.00000
···
···
0.0001
1.00000
0.01
0.99998
0.1
0.99833
I numeri suggeriscono che il valore del limite sia 1. Cerchiamo di darne una
prova formale.
Osserviamo dapprima che poiché sin x ed x sono entrambe funzioni dispari,
il loro rapporto è una funzione pari. E’ allora sufficiente considerare il limite
solo per valori positivi della variabile x, che indicheremo con il simbolo
lim
x→0+
sin x
=1
x
152
CAPITOLO 3. LE DERIVATE
Il seguente diagramma relativo alla circonferenza unitaria, ci aiuta a valutare
la situazione:
Consideriamo le aree dei triangoli OCP, OEQ e del settore di circonferenza
OEP. SI ha che
area (OCP ) ≤ area (OEP ) ≤ area (OEQ) .
Calcoliamo il valore di queste aree, si ha
base × altezza
cos x sin x
=
2
2
x
x
=
area (OEP ) = Area circonf erenza × F razione d0 arco = π ×
2π
2
tan x
base × altezza
=
area (OEQ) =
2
2
area (OCP ) =
ne segue che si ha
cos x sin x
x
tan x
≤ ≤
2
2
2
2
Poiché x > 0, moltiplicando per
si ha
sin x
x
1
cos x ≤
≤
sin x
cos x
Quando x → 0+ le quantità a sinistra e a destra tendono entrambe al valore
1, quindi anche quella nel mezzo deve fare lo stesso.
¥
Nota 83 L’idea di limite è abbastanza sofisticata. Lo sviluppo di una definizione
rigorosa e allo stesso tempo semplice da usare è stato storicamente un passo fondamentale per dare all’Analisi un fondamento rigoroso.
L’idea moderna di limite viene fatta discendere dal lavoro del matematico francese
Agostin Louis Cauchy, intorno al 1820, oltre 150 anni dopo lo sviluppo dato da
Newton e Leibnitz.
3.4. LIMITI E CONTINUITÀ.
153
Nota. Una funzione può non ammettere derivata in un punto del proprio
dominio. Un classico esempio di ciò è la funzione f (x) = |x| che non ammette
derivata nel punto x = 0. Il prossimo esempio mostra esattamente il perché di
questa affermazione già espressa graficamente.
Esempio 84 Sia f (x) = |x| . Mostrare, usando i limiti che f 0 (0) non esiste.
Soluzione. Per definizione
f 0 (0) = lim
x→0
f (x) − f (0)
|x|
= lim
x→0
x
x
se il limite esiste.
|x|
.
Per vedere che il limite non esiste consideriamo la funzione h (x) =
x
Ricordando che
½
x se x ≥ 0
|x| =
−x se x < 0
si ha che
h (x) =
½
1 se x > 0
,
−1 se x < 0
ma che h (0) non è definita. Il grafico della funzione è il seguente:
0
-1
x
1
Grafico di h (x) = |x| /x
Il limx→0 |x| /x non esiste; non c’è un unico valore al quale h (x) tende
quando x → 0. Il problema è quando x → 0 da sinistra (cioè per valori negativi
di x), h (x) → −1, ma quando da destra (cioè per valori positivi di x), h (x) → 1.
Poiché il limite non esiste non può neanche esistere, di conseguenza, f 0 (0) . ¥
3.4.2
Definizione di Limite - Informale e Preciso.
Sia L un numero finito. L’espressione
lim f (x) = L
x→a
(3.1)
significa informalmente che la funzione f (x) tende al valore L quando x
tende al valore a.
L’equazione (3.1) contiene due tipi di ingredienti:
154
CAPITOLO 3. LE DERIVATE
• i numeri reali a ed L;
• una funzione f definite per tutti gli x intorno ad x = a ma non necessariamente in x = a.
Definizione 85 (Informale) Se f (x) tende ad un singolo numero L quando
x tende ad a, allora limx→a f (x) = L.
Definizione 86 (Formale) Supponiamo che per ogni numero positivo ε (epsilon), esista un numero positivo δ (delta) tale che
|f (x) − L| < ε se 0 < |x − a| < δ .
Allora
lim f (x) = L
x→a
Osserviamo i seguenti dati:
Stima del Limite. Se limx→a f (x) = L, allora si ha che f (x) ≈ L quando
x ≈ a. Questo significa che possiamo valutare i limiti numericamente (valutando
il valore di f (x) per valori di x vicino ad a) e graficamente (tracciando il grafico
di f (x) per x vicino ad a).
f (a) ? Non è un Problema. E’ un fatto importante che limx→a f (x) = L
possa esistere anche se f (a) non è definita. Infatti, f (a) non è definita in molte
situazioni che per noi sono interessanti, quali per esempio
√
x−2
;
lim
x→4 x − 4
x2 − 9
;
x→3 x − 3
lim
lim
x→0
cos x − 1
.
x
Nessuna di queste funzioni è “definita per x = a”. In questo senso, il
problema di trovare il limite è quello di trovare un opportuno valore per f (a),
ammesso che esista.
Non Ci Sono Garanzie. Anche se f (a) esiste, non ci sono garanzie che
esista il limx→a f (x) e neanche (quando esiste) che esso sia uguale a f (a) .
L’operazione di limite non si occupa (non vede) del valore della funzione f nel
punto a . Che f (a) esista o meno la definizione di limite si riferisce solo a quei
valori di x per i quali è |x − a| > 0, cioè x 6= a.
Dal Greco all’Italiano. Riportiamo a parole ciò che la definizione formale
di limite afferma:
Possiamo affermare che f (x) differisce da L meno di ogni numero prescelto ε
richiedendo che x disti da a per meno di δ.
Comprendere bene l’idea di limite, come ripetuto, non è banale, ma il grafico
seguente può dare un idea di come ε e δ sono correlati.
3.4. LIMITI E CONTINUITÀ.
155
Graficamente la definizione formale significa che: Per ogni ε > 0 si può
scegliere una finestra centrata nel punto (a, L) di lunghezza 2δ e di altezza 2ε
dalla quale il grafico di f non esce né dalla sommità che dal fondo, eccetto
eventualmente che per x = a.
La scelta della lunghezza δ dipende dalla scelta dell’altezza ε.
Saremo spesso informali. In un corso elementare come questo, l’approccio informale al limite è quasi sempre adeguato. In corsi più avanzati, una
comprensione rigorosa del concetto di limite è essenziale. In tale situazione un
attento uso degli ε e δ è necessario. Noi siamo più interessati al concetto di
limite che al suo uso che alle dimostrazioni formali. Discuteremo quindi alcune proprietà teoriche dei limiti, ma principalmente come aiuto al loro calcolo
concreto.
Limiti Destri e Sinistri.
Abbiamo introdotto la definizione di limite e ne abbiamo visto l’applicazione
più importante: lo studio del limite di una funzione in un punto. Dobbiamo
anche studiare alcune varianti del concetto di limite che sono quelle di limite
sinistro, limite destro e i limiti che coinvolgono il concetto di ∞.
Ci limiteremo a dare definizioni “informali” di questi concetti.
Definizione 87 (Limite sinistro) limx→a− f (x) = L significa che f (x) → L
quando x → a da sinistra.
Definizione 88 (Limite destro) limx→a+ f (x) = L significa che f (x) → L
quando x → a da destra..
156
CAPITOLO 3. LE DERIVATE
Esempio 89 Nell’esempio (84) abbiamo visto che se h (x) = |x| /x , la funzione h (x) tende a −1 o a +1 a secondo che x tenda a 0 da sinistra o da destra..
Usando le definizioni sopra possiamo scrivere che
lim h (x) = −1
x→0−
e
lim h (x) = 1
x→0+
¥
Poiché questi due limiti sono diversi, abbiamo concluso che il limx→0 h (x)
non esisteva. Ne discende una conseguenza generale che stabiliamo di seguito.
Teorema 90 Il limx→a f (x) = L esiste se e solo se entrambi i limiti destro e
sinistro esistono e sono uguali tra di loro. In simboli
lim f (x) = L ⇐⇒
x→a−
3.4.3
lim f (x) = L = lim f (x) .
x→a−
x→a+
Continuità.
Affermare che una funzione f è continua su un intervallo I significa, parlando
intuitivamente, che “il grafico di f non presenta rotture per x ∈ I ”, o che
è lo stesso “che si può disegnare il grafico di f senza staccare la penna dal
foglio”. L’idea intuitiva, sebbene non sia una definizione, ci permette comunque
di lavorare su molte delle funzioni più semplici che incontriamo in questo corso.
Esempio 91 Ognuna delle funzioni che seguono è continua su tutto l’insieme
dei numeri reali (−∞, +∞) :
x2
; k (x) = |x|
x2 + 1
Il grafico di |x| ha uno spigolo in x = 0 ma questo non distrugge la continuità.
√
Esempio 92 Se consideriamo invece la funzione x si ha che questa è definita e continua nell’intervallo [0, +∞) . La funzione 1/x è definita e continua
nell’insieme (−∞, 0) ∪ (0, +∞) ma non è definita nel punto x = 0.
¥
f (x) = x2 ; g (x) = sin x ; h (x) =
Esempio 93 Consideriamo la funzione n (x) definita graficamente qui di seguito. Dire dove è continua n.
Soluzione. L’unica discontinuità si ha per x = −3. In particolare n è
continua in ogni intervallo che non contenga il punto x = −3.
¥
3.4. LIMITI E CONTINUITÀ.
157
Definizione di Continuità.
L’intuizione è sempre uno strumento fondamentale per lo studio della matematica, ma non è sufficiente. Per poter lavorare con tranquillità abbiamo bisogno
di una definizione precisa di continuità. L’idea di limite è quella che occorre,
per esprime in termini analitici il concetto geometrico intuitivo di “non rottura”
del grafico, in un punto.
Definizione 94 Sia f una funzione definita in un intervallo I contenente il
punto x = a. Se
lim f (x) = f (a)
x→a
allora f è continua in x = a. (Se a è l’estremo sinistro o destro dell’intervallo
considereremo solo il limite destro e sinistro rispettivamente).
Affermare che f è continua su I significa affermare che f è continua in tutti i
punti di I.
La definizione formale ci dice ancora quanto sia importante il ruolo giocato
dal concetto di limite.
Prestate molta attenzione ai fatti seguenti
Leggere Bene la Definizione. La definizione non afferma che f (a) è
uguale a limx→a f (x) . Essa afferma che per valutare se una funzione f è continua in x = a dobbiamo 1) calcolare limx→a f (x) e vedere se questo esiste o
meno; 2) calcolare f (a) ; 3) controllare se i risultati ottenuti in 1) ed in 2)
sono uguali tra loro. In questo caso si può affermare che la funzione è continua
in x = a.
In altri termini, la definizione ci dice che il comportamento di f per x = a “è
prevedibile”.
Continua, Dove? Una funzione f può essere continua se considerata
su un insieme, ma discontinua se considerata su di un altro insieme. L’affermazione f è continua può essere tecnicamente ambigua. Essa non dice dove f
è continua.
Per rendere non ambiguo il suo significato assumiamo che: A meno di una
esplicita limitazione, “continua” significa “continua su tutto il dominio di
definizione”.
Limiti Facili. Trovare i limiti per funzioni continue è molto facile. Infatti,
se f è continua in x = a , allora, la definizione di continuità ci dice che
x → a =⇒ f (x) → f (a) .
Esempio 95 Sia k (x) = x2 + 3x + 5. Trovare il limx→2 k (x) .
158
CAPITOLO 3. LE DERIVATE
Soluzione. Il problema appare facile. Né la formula né il grafico di k
suggeriscono sorprese strane nell’intorno del punto x = 2.
20
15
10
5
0
1
x
2
3
Grafico di k (x) = x2 + 3x + 5
La valutazione ovvia che limx→2 k (x) = 15 = k (2) è corretta poiché è continua
per x = 2.
¥
Discontinuità: Due Problemi Possibili.
Una funzione f è discontinua in x = a se, per qualche motivo, la condizione
posta dalla definizione non è soddisfatta. Questo è ciò che può succedere:
• Il limite limx→a f (x) non esiste; questo accade nell’Esempio (93) in x = 3
per la funzione n.
• Il limx→a esiste ma è diverso dal valore di f (a) .
Il prossimo esempio illustra questa patologia
Esempio 96 Consideriamo la funzione f così definita:
½
x se x 6= 0
f (x) =
1 se x = 0
Qual è il limx→0 f (x) ?
Soluzione. Il fatto che f (x) = 1 non è di nessuna importanza nel calcolo
del limite. Poiché è f (x) = x quando x 6= 0, si ha che
lim f (x) = lim x = 0 .
x→0
x→0
Si ha quindi che il valore del limite differisce dal valore della funzione nel
punto, per questa ragione, f è discontinua in x = 0. In certo senso, f ha un
valore “sbagliato” per x = 0.
¥
Qui di seguito sono presentati due problemi che riuniscono le idee di questo
paragrafo.
3.4. LIMITI E CONTINUITÀ.
159
Esempio 97 Sia
f (x) =
½
bx2 + 1 se x < −2
x
se x ≥ −2
Quali valori di b rendono la funzione continua?
sia
Soluzione. Perché la funzione sia continua nel punto x = −2 bisogna che
lim f (x) = f (−2) = −2
x→2−
Verifichiamo separatamente il limite destro e sinistro. Si ha:
f (x) → 4b + 1 per x → −2−
f (x) → −2
per x → −2+
Perché i due limiti siano uguali bisogna che sia 4b + 1 = −2, cioè b = −3/4. ¥
Esempio 98 Interpretare
eh − 1
x→0
h
lim
come derivata. Stimare il suo valore.
Soluzione. Se f (x) = ex , allora
eh − 1
f (h) − f (0)
= lim
.
x→0
x→0
h
h
lim
Allora, il limite dato è (per definizione) la derivata di f (x) = ex nel punto
x = 0.
¥
Verificate usando il metodo grafico che è f 0 (0) = 1.
160
3.4.4
CAPITOLO 3. LE DERIVATE
Esercizi.
1. Sia f (x) =
½
1 , se x è un intero
2 , se x non è un intero .
(a) Tracciare il grafico di f nell’intervallo [0, 5] ;
(b) Calcolare il limx→4 f (x) ;
(c) Calcolare il limx→5/2 f (x) ;
(d) Per quali valori di x il limite esiste? Perché?
2. Sia f la funzione il cui grafico è disegnato sotto. Usando il grafico calcolare
i limiti seguenti o dire perché il limite non esiste.
Grafico di f
(a) limx→0 f (x) ;
(b) limx→−3 f (x) ;
(c) limx→2− f (x) ;
(d) limx→2+ f (x) ;
(e) limx→2 f (x) ;
(f) limx→−2− f (x) ;
(g) limx→1+ f (x) ;
(h) limx→4+ f (x) ;
(i) limx→4− f (x) ;
(j) limx→3 f 0 (x) ;
(k) limx→1+ f 0 (x) ;
(l) limx→1− f 0 (x) ;
(m) limx→−3 f 0 (x) ;
(n) Su quali intervalli è continua f ?
3. Sia s (t) il coefficiente angolare della retta secante il grafico di f (x) =
x2 + x dal punto x = 3 al punto x = t.
(a) Trovare la formula per s (t) ;
3.4. LIMITI E CONTINUITÀ.
161
(b) Trovare limt→3 s (t) .
4. Supponiamo che la funzione f sia continua in x = 1 e che f (1) = −3.
Quanto vale limx→3 f (x)?
5. Supponiamo che f sia continua in x = 3 e che limx→3 f (x) = 13. Dire
quali delle seguenti affermazioni è vera o falsa. Giustificare la risposta.
(a) 3 è nel dominio di f ;
(b) f (3) = 13 ;
6.
7.
8.
9.
(c) limx→3− f (x) = 13.
½
sin x/x se x 6= 0
Sia f (x) =
Spiegare perché f
1
se x = 0.
½
sin x/ |x| se x 6= 0
Sia g (x) =
. Dire se g è
1
se x = 0.
Giustificare la risposta.
(
√ sin x
se x 6= 0
1−cos2 x
. Dire se h è
Sia h (x) =
1
se x = 0.
Giustificare la risposta.
½
ax + 1 se x < 2
. Dire per quali
Sia f (x) =
se x ≥ .2
x2
limx→2 f (x) .
è continua in 0.
continua in x = 0
continua in x = 0
valori di a esiste il
10. Supponiamo che f sia continua in x = 2 e che f sia definita da
½
ax2 + 3 se x < 2
f (x) =
3x − 5 se x ≥ .2
(a) Trovare il valore di a;
(b) Calcolare limx→3 f (x) ;
(c) Calcolare limx→0 f (x) ;
(d) Calcolare limx→2 f (x) ;
(e) Calcolare limx→1 f (x) .
 2
 x + a se x < −1
x + a2 se x = −1 .
11. Sia g (x) =

a − x se x > 1
(a) Trovare tutti i valori di a per i quali esiste il limx→−1 g (x) ;
(b) Trovare tutti i valori di a per i quali g è continua in x = −1.
½ 2
x − 2 se x < b
. Trovare tutti i valori di b per i quali
12. Sia h (x) =
x
se x ≥ .b
esiste il limx→b h (x) .
162
CAPITOLO 3. LE DERIVATE
13. Ognuno dei limiti sotto elencati rappresenta f 0 (a) per qualche funzione f
e qualche valore a. Identificare f ed a ed usare il metodo dell’ingrandimento grafico per valutare il valore del limite.
tan x
sin x
; limx→π
;
x
x−π
cosh −1
2x − 1
; limx→0
;
(b) limh→0
h
x−1
sin 3h
cos x
; limx→π/2
;
(c) limh→0
h
x − π/2
√
3
x−3
ln (h + 1)
; limh→0
.
(d) limx→27
x − 27
h
(a) limx→0
14. Supponiamo che sia limx→a f (x) = L.
Spiegare perché si ha che limh→0 f (a + h) = L.
15. Supponiamo che sia limh→0
che limx→a
f (a + h) − f (a)
= L. Spiegare perché si ha
h
f (x) − f (a)
= L.
x−a
16. Sia f (x) = x2 . Spiegare con cura ognuno dei seguenti passi per il calcolo
di f 0 (1) .
x2 − 1
x−1
(b) = limx→1 (x + 1)
(a) f 0 (1) = limx→1
(c) = 2.
17. Sia f (x) = x2 . Spiegare con cura ognuno dei seguenti passi per il calcolo
di f 0 (3) .
(3 + h)2 − 9
h
2
6h + h
h
(a) f 0 (3) = limh→0
(b) = limh→0
(c) = 6.
18. Usare la definizione di derivata per calcolare f 0 (4) di ognuna delle seguenti
funzioni:
(a) f (x) = 3 ; f (x) = 2x + 1 ; f (x) = x2 − 3x
√
(b) f (x) = x ; f (x) = x−1 ; f (x) = 3x−2 .
19. Supponiamo che f (x + y) = f (x) + f (y) + 3xy per tutti i valori reali di
f (h)
x e di y. Supponiamo inoltre che limh→0
= 37.
h
(a) Spiegare perché f (0) = 0 ;
3.4. LIMITI E CONTINUITÀ.
163
(b) Trovare un’espressione simbolica di f 0 (x) .
20. Supponiamo che f 0 (2) = 3. Calcolare il valore del limh→0
f (2 − h) − f (2)
.
h
21. Per ognuno dei limiti seguenti, usare un software per disegnare il grafico
di f , in modo da trovare un valore di δ che garantisca che |f (x) − L| < ε
quando |x − a| < δ.
(a) limx→2 3x = 6 ;
(b) limx→0
x+1
= 0.5 ;
x+3
1 − cos 2x
limx→0
= 2.
x2
limx→1
1 − cos x
= 0;
x
22. Nei limiti seguenti usare il valore di δ preassegnato per dimostrare i limiti.
(a) limx→2 x = 2, δ = ε ;
0, δ = ε;
limx→4 x2 = 16, δ = ε/10 ;
limx→0 |x| =
x2 − 9
= 6, δ = ε.
x−3
(c) Usare la definizione formale di limite per mostrare che
(b) limx→1 6 = 2, δ = 0.2; limx→3
lim 0.999999x 6= 1.
x→1
23. Sia f (x) =
½
x2 + 1 se x ≤ 0
.
−x
se x > 0
(a) Usare la definizione formale di limite per mostrare che f non è
continua in x = 0 [Sugg. f (0) − f (x) > 1 per x > 0].
(b) Mostrare che per ogni δ > 0 esiste ε > 0 tale che |f (x) − 1| < ε
quando 0 < |x| < δ.
(c) Perché il risultato di (b) non dimostra la continuità di f in x = 0 ?
[Confronta (b) con la definizione formale di limite].
164
CAPITOLO 3. LE DERIVATE
3.4.5
Limiti che Coinvolgono l’Infinito.
Nel paragrafo precedente abbiamo dato la definizione di limite, lo abbiamo applicato a diverse situazioni ed abbiamo infine introdotto il concetto di continuità. In questo paragrafo continuiamo lo studio dei limiti, introducendo un’altra
variante all’idea di limite, coinvolgendo il concetto di infinito. Cercheremo anche di dare un’interpretazione geometrica di questa estensione in termini di
asintoti.
Limiti all’Infinito, Limiti Infiniti e Asintoti.
Limiti all’infinito e limiti infiniti (non sono la stessa cosa), descrivono il comportamento di una funzione quando l’ingresso o l’uscita crescono o decrescono
senza limitazione. Definizioni di tipo informale ed esempi illustreranno l’idea.
Definizione 99 (Limiti all’Infinito)
limx→+∞ f (x) = L quando x → +∞, (quando x, cioè, cresce senza limitazioni).
Analogamente:
limx→−∞ f (x) = L significa che f (x) → L quando x → −∞, (quando x, cioè,
decresce senza limitazioni).
limx→∞ f (x) = L significa che f (x) → L quando |x| → +∞, (quando |x| , cioè,
cresce senza limitazioni).
Definizione 100 (Limite Infinito)
limx→a f (x) = +∞ significa che f (x) → +∞ quando x → a.
Analogamente:
limx→a f (x) = −∞ significa che f (x) → −∞ quando x → a.
limx→a f (x) = ∞ significa che |f (x)| → +∞ quando x → a.
Vediamo adesso alcuni esempi di applicazione delle definizioni date.
Esempio 101 Discutere il significato di ognuno dei seguenti limiti.
limx→∞
limx→0−
1
= 0;
x
1
= −∞ ;
x
limx→0
1
= +∞
x2
limx→∞ sin x non esiste.
Soluzione. Il limx→+∞ sin x non esiste perché la funzione seno continua
ad oscillare periodicamente tra i valori −1 ed 1 senza che si possa mai affermare che i valori della funzione tendano verso qualche valore definito. Per
quanto riguarda gli altri tre limiti, il disegno dei loro grafici può aiutarne
3.4. LIMITI E CONTINUITÀ.
165
l’interpretazione.
-2
20
20
10
10
0
x 2
-2
0
-10
-10
-20
-20
x 2
Grafico di y = 1/x2
Grafico di y = 1/x
Notare con attenzione il significato grafico di ognuno dei limiti all’infinito
e del limite infinito. Ognuno di loro corrisponde ad un asintoto orizzontale o
verticale.
¥
Asintoti e Limiti. La connessione tra asintoti, limiti all’infinito e limiti
infiniti può essere sintetizzata come segue:
Asintoti Orizzontali; Limiti all’Infinito. La retta orizzontale y = L è
un asintoto al grafico della funzione f se e solo se f tende ad L quando x → ±∞,
cioè se
lim f (x) = L
x→+∞
o
lim f (x) = L
x→−∞
Asintoti Verticali; Limiti Infiniti. La retta verticale x = a è un asintoto
orizzontale per il grafico della funzione f se (e solo se) f diverge quando x → a,
cioè se
lim f (x) = ±∞
x→a−
o
lim f (x) = ±∞
x→a+
Limiti ed Asintoti per Funzioni Razionali
L’informazione dell’esistenza o meno di asintoti per una funzione è importante per capire l’andamento complessivo del grafico.. Gli asintoti orizzontali
riflettono il comportamento della funzioni per valori grandi di |x| , mentre gli
asintoti verticali riflettono anomalie e punti di non definitezza al finito. Per
funzioni razionali (cioè rapporto di polinomi) il problema si presenta semplice.
Un Polinomio Può Avere Asintoti? I polinomi non hanno asintoti
verticali, visto che sono definiti su tutto R. Un asintoto orizzontale si ha, infatti, per un valore finito di x nell’intorno del quale la funzione tende ad essere
illimitata. Poiché la forma di un polinomio è la seguente
p (x) = a0 + a1 x + a2 x2 + · · · + an xn
166
CAPITOLO 3. LE DERIVATE
essi non possono crescere illimitatamente eccetto che per x → ±∞.
Solo un polinomio costante può avere un asintoto orizzontale. Se, per esempio p (x) = 4, allora il grafico di p è esso stesso orizzontale e quindi asintoto di
se stesso. Inoltre, i polinomi che non siano costanti hanno la seguente proprietà:
Affermazione: Se p (x) è un polinomio non costante, allora
limx→±∞ | p (x)| = +∞
Non dimostreremo questa affermazione, ma cercheremo di illustrarla.
Esempio 102 Sia p (x) = 2x3 − 53x2 − 123x. Come si comporta p quando
x → ±∞.?
Soluzione. E’ chiaro che quando x → +∞, 2x3 → +∞, −53x2 → −∞,
−123x → −∞, ma che cosa fa la somma dei tre termini? Per vedere il comportamento complessivo, conviene mettere in evidenza il termine di potenza
superiore, si ha
µ
¶
53 123
lim 2x − 53x − 123x =
− 2
lim x 2 −
x→+∞
x→+∞
x
x
µ
¶
53 123
3
=
lim x · lim 2 −
− 2
x→+∞
x→+∞
x
x
= +∞ · 2 = +∞ .
3
2
3
In modo del tutto simile
µ
¶
53 123
lim 2x − 53x − 123x =
− 2
lim x 2 −
x→−∞
x→−∞
x
x
µ
¶
53 123
3
lim x · lim 2 −
− 2
x→−∞
x→−∞
x
x
= −∞ · 2 = −∞ .
3
2
3
(in ognuno dei calcoli fatti abbiamo usato il fatto che il limite del prodotto è il
Vedremo
più prodotto dei limiti, quando questi esistono).I
avanti
questa
Algebra con il Simbolo di Infinito. Nell’esempio precedente abbiamo
proprietà.
usato due affermazioni che non abbiamo ancora discusso: 2 × +∞ = +∞ e
2 × −∞ = −∞. Qual’è il loro senso, che cosa significano? Ricordiamo che ∞ è
un simbolo, non un numero, quindi dobbiamo capire meglio che cosa significa
moltiplicare un simbolo per un numero. Nei due casi particolari, la risposta
appare intuitivamente chiara. Nella tavola seguente mettiamo insieme alcune
regole per l’uso del simbolo di infinito.
3.4. LIMITI E CONTINUITÀ.
Espressione
1/∞ = 0
167
Significato
OK, ma se con questo vogliamo intendere che limx→∞
perché non dirlo esplicitamente?
3·∞=∞
1
= 0,
x
OK come notazione abbreviata. Significa che se una quantità
cresce illimitatamente, il suo triplo si comporta nello stesso modo.
+∞ + ∞ = +∞
OK. Se due quantità crescono illimitatamente,
così fa la loro somma.
1/0 = +∞
ERRATO. La divisione per 0 non è definita;
inoltre 1/x → +∞ se x → 0+ , ma 1/x → −∞ se x → 0− .
+∞ − ∞ = 0
ERRATO. Per esempio, se x → +∞, x2 → +∞,
x → +∞, ma x2 − x → +∞.
∞/∞ = 1
ERRATO. Per esempio, se x → +∞,
x2 → +∞, x → +∞, ma x2 /x → +∞.
Asintoti Orizzontali di Funzioni Razionali: Controllare la Potenza
di Ordine Maggiore. Trovare gli asintoti orizzontali delle funzioni razionali
significa controllare i limiti all’infinito. Una semplice regola algebrica può essere
applicata:
Per trovare il limite all’infinito di una funzione razionale, mettere in evidenza la potenza più alta di x al numeratore ed al denominatore.
Vediamo come funziona:
Esempio 103 Consideriamo le tre funzioni razionali
r (x) =
2x3 − x
2x3 − x
2x3 − x
; s (x) = 3
; t (x) = 4
.
2
x −1
x −1
x −1
trovare gli asintoti orizzontali, se esistono.
Soluzione. Invece di usare i grafici (ma provate comunque a vederli usando
un qualche strumento) usiamo la strategia proposta sopra. Si ha:
¡
¢
x3 2 − 1/x2
2 − 1/x2
2x3 − x
=
x
;
r (x) = 2
= 2
x −1
x (1 − 1/x2 )
1 − 1/x2
¡
¢
x3 2 − 1/x2
2 − 1/x2
2x3 − x
=
;
s (x) = 3
= 3
x −1
x (1 − 1/x3 )
1 − 1/x3
¡
¢
x3 2 − 1/x2
1 2 − 1/x2
2x3 − x
=
;
t (x) = 4
= 4
x −1
x (1 − 1/x4 )
x 1 − 1/x4
168
CAPITOLO 3. LE DERIVATE
vediamo adesso che cosa accade quando x → +∞. E’ chiaro che si ha
r (x) → +∞ ; s (x) → 2 ; t (x) → 0 .
ne segue che s e t hanno asintoto orizzontale a y = 2 e y = 0 rispettivamente,
mentre r non ne ha.
¥
Asintoti Verticali di Funzioni Razionali: Controllare le Radici. Se
una funzione razionale ha asintoti verticali, questi vanno cercati tra le radici
del denominatore.
Esempio 104 Siano r, s, t come sopra. Trovare gli asintoti verticali.
Soluzione. Una funzione razionale ha asintoti verticali nei punti che annullano il denominatore, ma non il numeratore. (Se entrambi sono zero nello steso
punto , provvedere alla semplificazione). Per trovare gli asintoti fattorizziamo
il denominatore. Si ha
r (x) =
s (x) =
t (x) =
2x3 − x
2x3 − x
;
=
2
x −1
(x − 1) (x + 1)
2x3 − x
2x3 − x
;
=
x3 − 1
(x − 1) (x2 + x + 1)
2x3 − x
2x3 − x
;
=
x4 − 1
(x − 1) (x + 1) (x2 + 1)
la fattorizzazione del denominatore mostra che per ognuna delle tre funzioni
i punti x = ±1 sono valori singolari che annullano il denominatore, ma non il
numeratore. Ne segue che r e t hanno asintoti verticali nei punti x = 1 e x = −1
, mentre s ha asintoto verticale per x = 1. Per verificare il comportamento
delle funzioni nell’intorno degli asintoti bisogna valutare i limiti destri e sinistri
separatamente, perché il risultato potrebbe essere diverso.
Sappiamo che in ogni caso il risultato è infinito, il problema è: con quale
segno? Si tratta allora di capire il segno della funzione a sinistra ed a destra
dell’asintoto per sapere se il risultato del limite è +∞ o −∞.
Consideriamo r (x) . A sinistra di x = −1 si ha che:
2x3 − x < 0 , x + 1 < 0 , e x − 1 < 0 .
Quindi r (x) < 0, quindi limx→−1− r (x) = −∞. Un controllo simile sul segno di
r per valori di x maggiori di x = −1 mostra che r (x) → +∞ quando x → −1+ .
Si lascia per esercizio, la valutazione del segno delle funzioni s e t nell’intorno
degli asintoti verticali.
3.4. LIMITI E CONTINUITÀ.
169
Per finire, ecco i grafici delle tre funzioni:
5
-4
-2
0
5
2x
4
-4
-5
-2
0
5
2x
4
-4
-5
Grafico di r
Grafico di s
-2
0
2x
4
-5
Grafico di t
Asintoti per Altre Funzioni Algebriche. Così come le funzioni razionali,
altre funzioni algebriche possono ammettere asintoti, esattamente con lo stesso
di tipo di connessione con i limiti all’infinito ed i limiti infiniti. I calcoli per
la ricerca di questi limiti possono essere meno banali di quelli che sono stati
necessari per le funzioni razionali.
√
Esempio 105 Consideriamo la funzione f (x) = x2 + x − x, per x > 0.
Mostrare che f ammette asintoto orizzontale.
Soluzione. Il comportamento di f (x quando x → +∞) quando x → +∞
non è ovvio dalla formula, abbiamo bisogno di usare un po’ di manipolazione
algebrica per capire il comportamento della funzione.
√
Cominciamo con un trucco, moltiplichiamo e dividiamo per x2 + x + x, si ha
³√
´ ³√
´
´
³p
x2 + x − x
x2 + x + x
√
lim
x2 + x − x =
lim
x→+∞
x→+∞
x2 + x + x
x
=
lim √
x→+∞ x2 + x + x
x
³p
´
=
lim
x→+∞
x
1 + 1/x + 1
=
3.4.6
1
1
= .
lim p
x→+∞
2
1 + 1/x + 1
¥
Algebra dei Limiti.
Quando si calcolano i limiti, si danno spesso per scontati alcuni limiti semplici
o fondamentali e si cerca di ridurre i limiti più complicati a combinazioni di
quelli più semplici. Il prossimo esempio illustra il processo.
Esempio 106 Calcolare il limx→+∞
x2 + 3
.
2x2 − 5
170
CAPITOLO 3. LE DERIVATE
Soluzione. Cerchiamo sempre di usare la manipolazione algebrica per
ridurre il tutto. Si ha
x2 + 3
lim
x→+∞ 2x2 − 5
¡
¢
x2 1 + 3/x2
=
lim
x→+∞ x2 (2 − 5/x2 )
1 + 3/x2
=
lim
x→+∞ 2 − 5/x2
limx→+∞ 1 + limx→+∞ 3/x2
limx→+∞ 2 − limx→+∞ 5/x2
1
1+0
= .
=
2−0
2
¥
Nei calcoli precedenti, abbiamo usato diversi passaggi, apparentemente plausibili: limx→+∞ 3/x2 = limx→+∞ 5/x2 = 0, il limite del quoziente uguale al
quoziente dei limiti, ed infine che il limite della somma è la somma dei limiti.
Il seguente teorema giustifica i passaggi fatti sopra e ci dice come comportarci rispetto alle singole operazioni algebriche. FARE ATTENZIONE a come il
teorema è enunciato.
Teorema 107 (Algebra dei Limiti) Supponiamo che sia
lim f (x) = L
x→+a
e
lim g (x) = M ,
x→+a
dove L ed M sono numeri finiti. Sia k una costante. Si ha:
(i)
limx→+a k f (x) = k L
(ii)
limx→+a [f (x) + g (x)] = L + M
(iii)
limx→+a f (x) · g (x) = L · M
(iv) limx→+a
L
f (x)
=
g (x)
M
(se M 6= 0)
Osservazioni sul Teorema.
Perché valgono. Sebbene intuitive, le dimostrazioni rigorose delle regole
descritte dal Teorema hanno bisogno di un uso delle regole ε − δ. In questo
corso salteremo le dimostrazioni, ma una dimostrazione tipica di questo tipo è
descritta nell’Appendice I.
Limiti che Coinvolgono l’Infinito. Tutte le regole che abbiamo enunciato valgono anche per i limiti all’infinito, (cioè per x → ±∞) Esse valgono
anche per i limiti infiniti (cioè quando L = ±∞) tenendo conto delle cautele
legate alle regole dell’algebra degli infiniti.
Limiti “Noti”. Usando le regole algebriche per i limiti, possiamo risolvere
i limiti dati sempre che si conoscano i risultati di limiti più semplici. Per
3.4. LIMITI E CONTINUITÀ.
171
cominciare, considereremo noti i seguenti limiti:
Limiti Noti
limx→0 |x| = 0
limx→a x = a
per ogni reale a
limx→∞ xn = ∞
per ogni n > 0
limx→±∞
per ogni n > 0
1
=0
xn
Algebra delle Funzioni Continue
Se f e g sono funzioni continue, è ragionevole pensare che la somma, il prodotto,
il quoziente di funzioni continue, sia continuo. In realtà è così perché la continuità è definita attraverso il concetto di limite e quindi valgono le proprietà del
concetto di limite. Il seguente teorema chiarisce quanto detto sopra:
Teorema 108 (Algebra delle Funzioni Continue). Supponiamo che f e g
siano funzioni continue in x = a. Allora, ognuna delle seguenti funzioni
f +g
f −g;
e
f ·g
è continua in x = a.
Se g (a) 6= 0, allora anche f/g è continua in x = a.
Dimostrazione. Ognuna delle proprietà descritte sopra segue direttamente
dalle proprietà dei limiti. La prima per esempio, si dimostra così:
lim (f + g) (x) = lim f (x) + lim g (x) = f (a) + g (a) = (f + g) (a) .
x→a
x→a
x→a
Il risultato ottenuto è ciò che occorre per mostrare che la funzione f + g è
continua in x = a.
Composizione, Limiti e Continuità I limiti coinvolgono spesso funzioni
che sono costruite per composizione. E’ quindi utile sapere come interagiscono
le operazioni di limite e di composizione. Cominciamo, come sempre, a vedere
alcuni esempi.
Esempio 109 Discutere e trovare ognuno dei seguenti limiti.
¶
¶
µ
µ
sin x
x+1
L1 = lim ln (cos x) ; L2 = lim ln
; L3 = lim exp
.
x→+∞
x→0
x→0
x
x+2
Soluzione. Il primo limite è facile:
Quando x → 0, cos x → cos 0 = 1 , quindi
ln (cos x) → ln (cos 0) = ln 1 = 0 .
172
CAPITOLO 3. LE DERIVATE
Com’è che le cose hanno funzionato senza problemi? Perché le due funzioni
coinvolte nel limite, cos x e ln x sono funzioni continue nel loro dominio, ed in
particolare nel punto scelto. Quando x → 0, cos x → cos 0 perché la funzione
coseno è continua in x = 0; quando cos x → 1, ln (cos x) → ln 1 perché la
funzione ln x è continua in x = 1.
Per trovare L2 , ragioniamo in modo simile. Ricordiamo dapprima che
quando x → 0, (sin x) /x → 1, quindi
µ
¶
sin x
sin x
→ 1, quindi ln
→ ln 1 = 0.
Quando x → 0,
x
x
La continuità ci aiuta ancora, poiché la funzione ln x è continua in x = 1, si ha
che
¶
µ
sin x
sin x
→ 1 =⇒ ln
→ ln 1 .
x
x
Il limite L3 è un limite “all’infinito”, ma si applicano per lui le stesse regole
che valgono per L1 ed L2 :
¶
µ
x+1
x+1
x → +∞ =⇒
→ 1 =⇒ exp
→ exp (1) = e .
x+2
x+2
Ancora una volta, la chiave per risolvere il problema è la continuità. La seconda
implicazione vale perché la funzione esponenziale è continua in x = a.
¥
Limiti di Funzioni Continue: un Principio Generale. Alle tre funzioni dell’esempio precedente si applica lo stesso principio fondamentale che
stabiliamo adesso nella sua forma generale (la sua dimostrazione formale, che
omettiamo, fa ricorso alla definizione ε − δ di limite):
Teorema 110 (Limite della Composizione di Funzioni). Siano f e g
funzioni tali che limx→a g (x) = b e f è continua in x = b. Allora,
³
´
lim (f ◦ g) (x) = lim f (g (x)) = f lim g (x) = f (b) .
x→a
x→a
x→a
Composizione di Funzioni Continue. Ricordiamo che, per definizione,
una funzione f è continua in x = a se e solo se limx→a f (x) = f (a). Con questa
definizione ed il teorema precedente è facile dimostrare che la composizione di
funzioni continue è continua. Più precisamente:
Teorema 111 Supponiamo che g sia continua in x = a ed f sia continua in
g (a) . Allora f ◦ g è continua in x = a.
Dimostrazione. Se x → a, g (x) → g (a) poiché g è continua in a. Quando
g (x) → g (a) , f (g (x)) → f (g (a)) perché f è continua in g (a) . Mettendo tutto
insieme si ha:
x → a =⇒ (f ◦ g) (x) → (f ◦ g) (a) .
Questo è quanto dovevamo dimostrare.
3.4. LIMITI E CONTINUITÀ.
173
Limiti e Disuguaglianze: Il Principio della Compressione (o dei Carabinieri o del Sandwich). Le regole algebriche sui limiti non aiutano quando
si tratta di calcolare limiti del tipo
µ ¶
1
lim x · sin
x→0
x
e
sin x
.
x→∞ x
lim
Il prodotto dei limiti non si applica al primo caso perché il termine sin (1/x) non
ha limite quando x → 0 ed il secondo perché sin x non ha limite per x → ∞.
Proviamo a calcolarli direttamente.
L’idea è quella di trovare due disuguaglianza in modo da “comprimere”
la funzione che ci interessa tra due µfunzioni
più semplici. Nel primo caso,
¶
1
≤ 1, si ha che per ogni x è vero che
ricordando che per ogni x è −1 ≤ sin
x
µ ¶
1
≤ |x| .
− |x| ≤ x sin
x
Tracciamo il grafico, per convincersi che le disuguaglianze sono vere:
Limite per Compressione
Quando x → 0 i termini sinistro e destro µ
delle
¶ disuguaglianze tendono a
1
zero. Compresso tra − |x| e |x| il termine x sin
ha una sola possibilità:
x
x sin
µ ¶
1
→ 0 quando x → 0 .
x
Enunciamo adesso un Teorema generale. Il grafico precedente lo rende
ragionevole; noi omettiamo la dimostrazione formale.
174
CAPITOLO 3. LE DERIVATE
Teorema 112 (Il Principio di Compressione). Supponiamo che si abbia
f (x) ≤ g (x) ≤ h (x)
per tutti gli x in un intorno di x = a. Se limx→a f (x) = limx→a h (x) = L ,
allora si ha
lim g (x) = L .
x→a
Nota. Il Principio della Compressione è concettualmente facile da comprendere; la parte difficile, in pratica, è scegliere le funzioni f e h in modo
conveniente.
µ ¶
1
.
Esempio 113 Calcolare limx→+∞ x sin
x
Soluzione. Vediamo dapprima cosa ci dice il grafico della funzione per
valori di x grandi
1
.9998
.9996
.9994
.9992
0.999
.9988
.9986
.9984
20
40
x 60
80
100
Grafico di x sin (1/x) per grandi valori di x
L’intuizione ci dice che la funzione tende al valore 1. Cerchiamo adesso di
verificare algebricamente il risultato.
Quando x → +∞, 1/x → 0, quindi si ha che
lim
x→+∞
ma
sin (1/x)
= 1,
1/x
sin (1/x)
sin (1/x)
= x sin (1/x) , da cui segue che
1/x
1/x
lim x sin (1/x) = 1 .
x→+∞
¥
3.4. LIMITI E CONTINUITÀ.
3.4.7
175
Esercizi
1. Usare la calcolatrice (o il calcolare) per stimare i seguenti limiti.
3
5
x2 + 1
x2 + 1
; limx→−∞
;
(a) limx→+∞ 2 ; limx→+∞ √ ; limx→+∞
x
x
x
x
√
x
; limx→0+ x log10 x ; limx→0+ sin (sin x) ;
(b) limx→0+
x
2x
2x
x2
x2
(c) limx→+∞ 2 , limx→−∞ 2 ; limx→+∞ x ; limx→−∞ x .
x
x
2
2
2. Usare i grafici per valutare se i seguenti limiti esistono. Stimare il valore
di quelli che esistono
2000x
3x − 3
3x − 3
;
lim
;
lim
x→−∞ x
x→+∞ x
100x2 + sin x
2 −2
2 −2
2
1 − cos (3x)
1 − cos x
.
; limx→0
x2
x
(a) limx→+∞
(b) limx→0
3. Supponiamo che limx→1 f (x) = 4 e limx→1 g (x) = −3. Usare queste
informazioni per calcolare i seguenti limiti
(a) limx→1 (f (x) + g (x)) ;
(b) limx→1 (f (x) − g (x)) ;
f (x) + 2
.
(c) limx→1
f (x) g (x)
√
4. Sia f (x) = 3 x. spiegare perché limx→0 f 0 (x) = ∞.
5. Supponiamo che f (x) sia una funzione periodica non costante. Spiegare
perché limx→±∞ f (x) non esiste.
6. Disegnare un possibile grafico di una funzione che possiede tutte le proprietà elencate.
(a)
i.
ii.
iii.
iv.
v.
vi.
f ha come dominio (−7, +∞) ;
f ha rango (−∞, 3) ;
f (−1) = 0 ; f (0) = 0 ; f (5) = 0;
limx→−7+ = −∞ ;
limx→2 f (x) = −3 ;
limx→+∞ f (x) = 2 .
7. Disegnare un possibile grafico di una funzione che possiede tutte le proprietà elencate.
(a)
i. f ha come dominio R;
ii. f ha immagine (−3, +∞) ;
iii. limt→2 f (t) = −2;
176
CAPITOLO 3. LE DERIVATE
iv. limt→+∞ f (t) = −3;
v. limt→−∞ f (t) = 3.
8. Sia P = (0, 1) e Q un punto mobile sull’asse delle x. Sia r la retta passante
per P e Q.
(a) Trovare come varia il coefficiente angolare m di r al variare di Q;
(b) Trovare il limite quando il punto Q → ±∞ ;
(c) Supponiamo che Q tenda verso l’origine, si può affermare che esiste
un limite per m ? Giustificare la risposta.
9. Sia O = (0, 0) e Q un punto mobile sulla retta y = 2x + 3.Sia r la retta
passante per O e Q.
(a) Trovare come varia il coefficiente angolare m di r al variare di Q;
(b) Trovare il limite quando la coordinata x del punto Q → ±∞.
10. Mostrare che esiste un solo valore di k ≥ 1 per il quale limx→0
esiste finito. Trovare il valore di k e calcolare il limite.
sin (2 sin x)
xk
11. Siano p (x) = (x + 1) (2 − x) e q (x) = x15 − 7x14 + 46. Calcolare ognuno
dei seguenti limiti
(a) limx→−∞ p (x) ;
(b) limx→−∞ q (x) ;
limx→+∞ p (x) ;
limx→+∞ q (x) .
12. Supponiamo che r (x) sia un polinomio di grado n tale che limx→−∞ r (x) =
limx→+∞ r (x) = −∞. Si può dire se n è pari o dispari? Spiegare il perché.
13. Sia h una funzione che ha un asintoto verticale in x = 3 e tale che
limx→−∞ h (x) = +∞, mentre limx→+∞ h (x) = −1.
(a) Dire se h possiede un asintoto orizzontale e qual è.
(b) Può h essere una funzione razionale? Spiegare la risposta.
14. Ogni funzione razionale r (x) si comporta all’infinito come axn , con a ∈ R
e n intero, nel senso che
r (x)
= 1.
x→±∞ axn
lim
Per esempio r (x) =
x
si comporta come −x−1 , infatti si ha
1 − x2
x
x2
lim 1 −−1
x→±∞ −x
=
=
−x2
= lim
x→±∞ 1 − x2
x→±∞
lim
lim
x→±∞
1
1
1− 2
x
=1
−x2
µ
¶
1
2
−x 1 − 2
x
3.4. LIMITI E CONTINUITÀ.
177
Trovare i valori appropriati di a e di n per le funzioni razionali seguenti:
4x2 + 3x
;
3x4 + 2x2 − 6
x4 − 4x3 + 5x2 − 6x + 7
;
(b) q (x) =
3x4 − 6x2 + 8
2x5 − 3x4 + 4x3 − 5x2 + 6x − 7
(c) r (x) =
.
3x2 − 4x + 5
(a) p (x) =
15. Calcolare i seguenti limiti
√
x2 + 1 − x ;
√
(b) limx→+∞ x2 + x − x ;
(a) limx→+∞
√
x2 + 1 − x;
√
limx→−∞ x2 + x − x.
limx→−∞
16. Dare esempi di polinomi p (x) e q (x) con limx→+∞ p (x) = limx→+∞ q (x) =
+∞, tali che:
p (x)
= +∞ ;
q (x)
p (x)
= 2;
limx→+∞
q (x)
p (x)
= 0;
limx→+∞
q (x)
p (x)
= 1;
limx→+∞
q (x)
limx→+∞ (p (x) − q (x)) = 3.
(a) limx→+∞
(b)
(c)
(d)
(e)
17. Sia p (x) = axn + q (x), dove q (x) è un polinomio di grado m < n.
q (x)
?
xn
q (x)
(b) Quanto vale limx→−∞ n ?
x
(c) Se a > 0 e n è pari quanto vale il limx→+∞ p (x) ?
(a) Quanto vale limx→+∞
(d) Se a > 0 e n è pari quanto vale il limx→−∞ p (x) ?
(e) Come rispondereste a (c) e (d) se n è dispari ?
18. Spiegare perché limx→+∞ cos x non esiste.
19. calcolare i seguenti limiti, se esistono:
(a) limx→+∞
(b) limx→+∞
sin x
;
x
x3
.
2 + cos x
178
CAPITOLO 3. LE DERIVATE
20. Supponiamo che limx→a f (x) e limx→a g (x) non esistano. Trovare due
funzioni f e g tali che i seguenti limiti esistono, oppure spiegare perché
non è possibile.
(a) limx→a (f (x) + g (x)) ;
(b) limx→a (f (x) · g (x)) .
21. Sia f una funzione definita su R. Quali delle seguenti affermazioni è
sicuramente vera, potrebbe essere vera, è sicuramente falsa?
(a) limx→a f (x) = f (a) ;
f (x)
= 2, allora f (0) = 0 ;
(b) Se limx→0
x
f (x)
= 1, allora limx→0 f (x) = 0 ;
(c) Se limx→0
x
(d) Se limx→1− f (x) = 1 e limx→1+ f (x) = 3, allora e limx→1 f (x) = 2;
(e) Se limx→2 f (x) = 3 allora 3 è un elemento del rango di f ;
f (x) − f (0)
= 3, allora f 0 (0) = 3.
(f) Se limx→0
x