Teorema. Le bisettrici di due angoli esterni di un triangolo e dell

09/01/2016
Teorema. Le bisettrici di due angoli esterni
di un triangolo e dell’angolo interno non
adiacente passano per uno stesso punto
Def.: In un
triangolo, il
punto di
incontro delle
bisettrici di due
angoli esterni e
dell’angolo
interno non
adiacente si
chiama
excentro.
1
09/01/2016
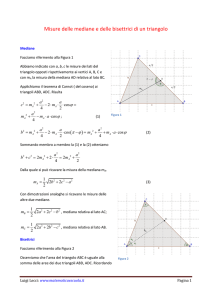
Teorema.
Le tre mediane di un
triangolo passano per uno
stesso punto, che divide le
mediane in due parti, di
cui quella avente per
estremo un vertice è
doppia dell’altra.
Dim.: Disegniamo le mediane AN e BM.
Siano D e E i punti medi di OA e OB
DE//AB, DE metà di AB; MN//AB DE//AB, DE≡MN
DENM è un parallelogramma le sue diagonali si tagliano a
metà: OM≡OE, ON≡OD
Le mediane AN e BM si intersecano in un punto che le divide in
due parti, di cui quella con estremo un vertice doppia dell’altra
Analogamente per le mediane CL e BM
Il segmento BM è tagliato in due segmenti, l’uno doppio
dell’altro
L’unico punto che soddisfa tale proprietà è O
Le tre mediane passano per uno stesso punto
2