BISETTRICI E INCENTRO
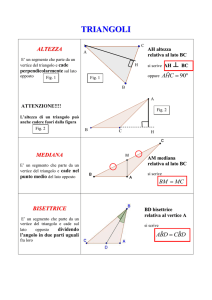
Consideriamo un qualunque triangolo e tracciamo un segmento AD che partendo dal vertice A raggiunga il
lato opposto dividendo a metà l’angolo in A
Il segmento AD si chiama bisettrice dell’angolo A.
Possiamo quindi dire che si chiama bisettrice di un triangolo relativa ad un vertice quel segmento che
unisce il vertice con il lato opposto dividendo a metà l’angolo.
Poiché un triangolo ha 3 vertici e tre angoli , le bisettrici di un triangolo saranno sempre 3.
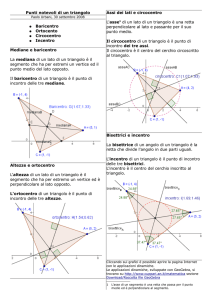
In qualsiasi triangolo le tre bisettrici si incontrano in un unico punto detto INCENTRO.
L’incentro è sempre interno al triangolo ed ha sempre la stessa distanza da ciascuno dei lati.
MEDIANE E BARICENTRO
Consideriamo un qualunque triangolo e tracciamo un segmento AE che partendo dal vertice A raggiunga il
punto medio del lato opposto.
Il segmento AE si chiama mediana relativa al lato BC.
Possiamo dunque affermare che si chiama mediana di un triangolo relativa ad un lato quel segmento che
unisce il punto medio del lato con il vertice opposto.
Poiché un triangolo ha 3 lati , le mediane di un triangolo saranno sempre 3.
In qualsiasi triangolo le tre mediane si incontrano in un unico punto detto BARICENTRO.
Il baricentro è sempre interno al triangolo.
Un’altra proprietà del baricentro è data dal fatto che esso divide ogni mediana in due parti di cui una è il
doppio dell’altra. Nel triangolo sotto il baricentro O fa sì che:
AO = 2 OD
CO = 2 OF
BO = 2 OE
Calcolo dell’area e del perimetro del triangolo