Elettronica - oscillatori
OSCILLATORI SINUSOIDALI
1 — Generalità
Gli oscillatori sono circuiti che assorbono potenza continua e generano tensioni variabili periodicamente con ampiezze e
frequenze costanti. Queste tensioni possono essere sinusoidali con alto grado di purezza d'onda, oppure possono essere quadre,
triangolari o di altra forma con un gran numero di armoniche.
Si hanno così, rispettivamente, oscillatori sinusoidali, multivibratori, oscillatori a dente di sega, e così via. In questo capitolo
ci occuperemo di oscillatori sinusoidali che trovano particolare applicazione sia nei trasmettitori che nei ricevitori come generatori di
tensione a radio frequenza. Per la produzione di tensioni sinusoidali si utilizzano in prevalenza circuiti risonanti mantenuti in stato di
eccitazione da transistori o tubi elettronici.
I circuiti risonanti sono sedi di oscillazioni smorzate. Se si vogliono ottenere oscillazioni persistenti occorre rifornire il circuito,
oscillazione per oscillazione, dell'energia che inevitabilmente viene dispersa per effetto Joule e di quella che, eventualmente, viene
prelevata.
La possibilità che un sistema elettrico possa oscillare si è già intravisto nello studio della reazione. In quell'occasione abbiamo
osservato che quando il segnale di reazione è in fase con quello d'ingresso, e si verifica
A
1 (1)
l'amplificazione reazionata diventa infinita, per cui abbiamo un segnale di uscita diverso da zero con segnale d'ingresso nullo. Ciò
significa che la tensione di uscita da luogo ad una tensione di reazione all'ingresso dell'amplificatore tale, da generare la stessa
tensione di uscita senza segnale esterno. Infatti dallo schema a blocchi di fig.1 si ricava
A
E i E r
E u
Ei
e quindi la (1).
Pertanto affinchè un sistema possa oscillare, occorre che l'amplificazione prodotta dall'elemento amplificatore (A) sia uguale
all'attenuazione
1
prodotta dall'elemento di reazione, e che lo sfasamento introdotto dall'elemento amplificatore sia opposto a
quello introdotto dall'elemento di reazione. Occorre però osservare che la (1) è la condizione per mantenere un'oscillazione già
esistente m uscita. Un oscillatore, invece, al momento dell'innesco, non essendo eccitato da nessun segnale esterno, non fornisce che
una debolissima oscillazione nata nel circuito risonante per effetto di un inevitabile transitorio iniziale.
Quindi, affinché tale oscillazione aumenti di ampiezza, occorre che il guadagno A
dell'anello aperto di fig.1, sia maggiore
di uno, cioè
A
1 (2)
Infatti con questa condizione l'amplificazione A è maggiore dell'attenuazione
1
per cui il segnale di reazione, se riportato
con fase opportuna, da luogo ad un segnale di uscita maggiore di quello da cui era derivato. Evidentemente l'aumento non può essere
infinito perché intervengono inevitabilmente fenomeni di saturazione negli elementi attivi che tendono a diminuire l'amplificazione
fino a soddisfare la relazione (1). La (1) pertanto, costituisce la condizione di equilibrio dinamico di mantenimento delle oscillazioni,
mentre la (2) costituisce la condizione d'innesco o di esaltazione delle oscillazioni.
In fig.2 sono riportate sia la caratteristica di uscita-entrata del blocco amplificatore
E u A
Ei
che è sensibilmente lineare nel primo tratto e non lineare nel tratto successivo, sia la caratteristica entrata-uscita del blocco di
reazione
1
Eu
Ei
che è lineare avendo supposto che il blocco di reazione sia costituito da elementi indipendenti dalla frequenza e dalla tensione (=
cost.).
Dalla figura si osserva che nel punto P si raggiunge la condizione di equilibrio dinamico A = 1/ e che ciò si può ottenere
solo se nel tratto iniziale si verifica A > 1 /
.
Pag. 1
Elettronica - oscillatori
Si osserva inoltre che quando A
è molto maggiore di uno il punto di funzionamento P interessa il tratto non lineare della
caratteristica EU = A Ei , oscillatori non lineari, mentre quando A
è leggermente maggiore di uno il punto di
funzionamento si trova nel tratto iniziale sensibilmente lineare, oscillatori lineari.
In quest'ultimo caso però l'ampiezza delle oscillazioni è piuttosto limitata, ed inoltre piccole variazioni nei parametri degli
elementi attivi possono bloccare le oscillazioni. Spesso, quando si desidera far funzionare un oscillatore in maniera lineare, si ricorre
ad altri accorgimenti tra cui quello di introdurre nella rete di reazione opportuni elementi non lineari.
2 — Oscillatori di Meissner
Gli oscillatori di Meissner sono costituiti da un circuito risonante alimentato da un transistore. Il circuito di reazione è
costituito da un accoppiamento indiretto per mutua induzione. In fig. 3 è riportato un tipo di oscillatore di Meissner a transistore. Il
suo funzionamento si può spiegare in maniera intuitiva come segue.
All'atto dell'innesco, per il transitorio iniziale, nel circuito risonante nasce un'oscillazione. Una parte di essa, per mutua
induzione, viene trasmessa alla base che è polarizzata in senso diretto mediante il partitore R1 e R2 per cui viene amplificata e sfasata
di 180°.
Se le due bobine L1 e L 2 sono avvolte in modo tale da introdurre uno sfasamento di 180° tra tensione di collettore e tensione di
base, il segnale ritorna sull'elemento di comando in fase. Pertanto se l'accoppiamento è ben regolato e l'amplificazione del transistore
è sufficiente, cioè se si verifica la condizione (2), l'oscillazione iniziale risulta rinforzata. Via via che aumenta l'ampiezza di queste
oscillazioni aumenta pure l'ampiezza di quella di base che tendono a caricare il condensatore C2 in modo tale da polarizzare in senso
inverso la base. Il valore di questa polarizzazione finisce quindi per oltrepassare quello del potenziale di interdizione Vb = 0 e di
conseguenza il transistore viene a lavorare in classe C. Possiamo allora concludere che l'oscillatore funziona in classe C (regime non
lineare) e la polarizzazione automatica di base R 2 C2 regola la tensione di collettore in maniera che il circuito venga rifornito
esattamente dell'energia di cui abbisogna impedendo quindi che le oscillazioni si smorzino o si amplifichino.
La frequenza di lavoro dell’ oscillatore non è esattamente uguale a quella del circuito risonante f0 data da:
Pag. 2
Elettronica - oscillatori
1
(3)
f 0
2
L
C
ma dipende anche dagli elementi circuitali.
Tale dipendenza è comunque di piccola entità, per cui agli effetti pratici si può considerare come frequenza di lavoro quella data
dalla (3).
Ci sono molti altri schemi di oscillatori di Meissner a seconda di come è inserito il circuito risonante rispetto all'elemento
amplificatore e di come è alimentato. Così, per esempio, in fig. 4 è riportato l'oscillatore di Meissner con il circuito risonante in base,
il cui funzionamento è del tutto simile al precedente.
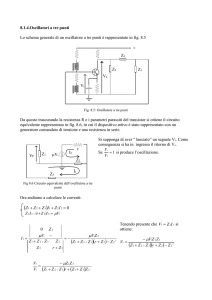
3 — Oscillatori a tre punti
Gli oscillatori a tre punti rappresentano una categoria di oscillatori in cui l'accoppiamento tra circuito di uscita e circuito
d'ingresso è diretto, fig,5.
Si sono omessi per semplicità i circuiti di alimentazione. polarizzazione e stabilizzazione termica.
Risolvendo analiticamente i circuiti di fìg.5 si trova che la condizione necessaria, (ma non sufficiente) perché si verifichino in
essi delle oscillazioni, è che le impedenze tra base ed emettitore Z b e tra collettore ed emettitore Z c siano dello stesso tipo, induttiva
o capacitiva, mentre quella tra collettore e base Z a sia di tipo diverso e cioè rispettivamente capacitiva o induttiva. La condizione
diventa sufficiente quando tali impedenze assumono valori opportuni.
Si hanno così due tipi di oscillatori: oscillatori tipo Hartley, fig. 6 a ed oscillatore tipo Colpitts, fig.6 b. E' facile verificare che
in entrambi i casi è verificata la condizione generale d'innesco.
Nell'oscillatore tipo Hartley l'accoppiamento tra circuito di collettore e quello di base è realizzato mediante partitore induttivo
(accoppiamento ad autotrasformatore), mentre in quello tipo Colpitts è realizzato mediante partitore capacitivo. Da osservare
l'alimentazione in parallelo per entrambi i circuiti. Nel circuito di fig, 6 b, manca il condensatore di accoppiamento Ca in quanto la
sua funzione è assolta dal condensatore C".
Occorre inoltre notare che la resistenza R2 del gruppo di polarizzazione automatica di base non è in parallelo a C2 ma è
collegata direttamente tra la base e l'emettitore e ciò perché altrimenti la corrente media di base non potrebbe circolare a causa del
condensatore C’.
Pag. 3
Elettronica - oscillatori
Per quanto riguarda il funzionamento si può osservare che l'oscillazione iniziale, che nasce ai capi del circuito risonante, si
ripartisce tra collettore ed emettitore e tra base ed emettitore. Quest'ultima viene amplificata e rinforza quella tra collettore ed
emettitore, fino a raggiungere la condizione di equilibrio dinamico.
La frequenza di lavoro è data approssimativamente da quella del circuito risonante e cioè
1
f0
(4)
2
Leq
C
per l'oscillatore tipo Hartiey con Leq= L 1 + L 2 + 2M e
1
f0
(5)
2
L
C eq
C'
C ''
C ' C ''
per l'oscillatore tipo Colpitts con C eq
4 — Stabilità di frequenza degli oscillatori
Come abbiamo già osservato, la frequenza degli oscillatori che coincide praticamente con quella di risonanza del circuito
risonante LC, in effetti dipende anche dagli altri elementi circuitali. Essa, pertanto subisce piccole fluttuazioni quando si verificano
variazioni di parametri caratteristici degli elementi attivi, degli elementi circuitali, della tensione di alimentazione, ecc.
Infatti, poiché tali variazioni portano a parità di frequenza a variazioni di fase che smorzerebbero le oscillazioni, l'oscillatore
slitta in frequenza in modo tale da realizzare uno sfasamento complessivo dell'anello A nullo e mantenersi cosi in oscillazione anche
se con una frequenza diversa. Si definisce pertanto, stabilità di frequenza il rapporto tra la variazione di fase e la variazione relativa
di frequenza:
d
d
f 0
(6)
Sf
df
df
f0
dove f0 è la frequenza media di oscillazione.
Evidentemente tanto più grande è Sf tanto più stabile in frequenza è l'oscillatore. Infatti ciò significa che a parità di variazioni di
fase si hanno piccole variazioni di frequenza. A1 limite quando Sf diventa infinito. l'oscillatore è completamente stabile in frequenza.
Molti accorgimenti di carattere meccanico ed elettrico vengono presi per aumentare la stabilità degli oscillatori.
In particolare si scelgono induttori e condensatori con bassissimo coefficiente di temperatura o con coefficienti di temperatura
opposti in modo che le variazioni di uno compensino le variazioni dell'altro.
Si usano circuiti risonanti con alto Q perché più grande è il coefficiente di risonanza maggiori sono le variazioni di fase
introdotte dal circuito risonante per piccole variazioni di frequenza.
Affinché il Q non sia diminuito per effetto di un carico, l'oscillatore non deve mai fornire potenza. Quando occorre erogare
potenza è necessario ricorrere prima ad uno oscillatore pilota, il quale, a sua volta, aziona apposito amplificatore.
Con questi ed altri accorgimenti si ottengono instabilità dell'ordine di 0.01 % ovvero 10 4 . Ciò significa che un oscillatore,
operante sulla frequenza di 1000 KHz, ha una frequenza di oscillazione variabile da 999,9 KHz a 1000,1 KHz. Quando si richiedono
instabilità inferiori bisogna ricorrere agli oscillatori controllati a quarzo.
Pag. 4
Elettronica - oscillatori
5 — Piezoelettricità — Quarzo piezoelettrico
Per comprendere la funzione del quarzo negli oscillatori, è opportuno richiamare brevemente il fenomeno fisico della piezoelettricità e
la costituzione del quarzo. La piezoelettricità è la proprietà che presentano alcuni cristalli isolanti di polarizzarsi elettricamente
quando sono soggetti a deformazioni elastiche per effetto di qualsiasi azione meccanica. Il fenomeno si chiama effetto diretto.
L'azione meccanica può esercitarsi per compressione, per trazione, per flessione, per torsione, per scorrimento ecc.
Le cariche elettriche eteronime che si manifestano sulle facce opposte del cristallo, sono cariche libere la cui somma algebrica è nulla.
La suddetta proprietà è reversibile e cioè polarizzando elettricamente il cristallo esso si deforma. Questo fenomeno si chiama
effetto inverso.
Il fenomeno piezoelettrico si riscontra in quasi tutti i cristalli. Quelli presi in maggior considerazione sono però il quarzo, la
tormalina ed il sale di La Rochelle.
In quest'ultimo cristallo l'effetto piezoelettrico è tortissimo e precisamente quasi 500 volte più di quello riscontrato negli altri
cristalli.
Esso però presenta l'inconveniente che l'intensità di polarizzazione è funzione molto complessa delle azioni meccaniche.
In pratica, tenuto conto delle ottime qualità meccaniche presentate, e della relativa facilità con cui è possibile trovare grossi
cristalli, negli oscillatori si impiega solo il quarzo.
Il quarzo piezoelettrico si presenta come grossi cristalli aventi all'incirca la forma di un prisma esagonale terminante a piramidi,
fig. 7. Esso presenta:
a. Un asse ottico Z di simmetria ternaria.
b. Tre assi elettrici X a 120° l'uno dall'altro che, nel caso teorico di cristallo a sezione perfettamente esagonale, risultano normali agli
spigoli e passanti per essi.
c. Tre assi meccanici Y che nella stessa ipotesi di cui alla lettera precedente risultano normali alle facce.
Se da questo massello di quarzo si taglia una serie di parallelepipedi, o una serie di piastrine, che comunemente si chiamano
cristalli, o quarzi, le proprietà piezoelettriche che essi presentano dipendono dalla giacitura delle facce rispetto agli assi del massello
di provenienza, e cioè dalla giacitura dei tagli.
Fra i tagli più significativi ricordiamo qui:
a. II taglio X, o di Curie, nel quale le piastrine sono tagliate parallelamente ll'asse ottico Z, e ad un'asse meccanico Y. Le loro
Pag. 5
Elettronica - oscillatori
superfici principali sono normali all'asse X, fig.8.
b. II taglio Y a 30°, nel quale le piastrine sono tagliate parallelamente all'asse ottico Z, e ad un asse elettrico X. Le loro superfici
principali sono evidentemente normali all'asse Y, fig,9.
c. Il taglio R, ovvero AT a 35°, nel quale le piastrine sono tagliate parallelamente all'asse elettrico X ed inclinate di 35° rispetto
all'asse ottico Z , fig10.
Consideriamo per esempio un cristallo di taglio X, e comprimiamolo in direzione dell'asse elettrico, fig.11 a.
Il cristallo si deformerà assottigliandosi in direzione dell'asse elettrico X e dilatandosi in direzione dell'asse meccanico Y, mentre
nessuna deformazione subirà in direzione dell'asse ottico Z.
Contemporanemente le due facce normali a X si polarizzeranno elettricamente. Eguale polarizzazione subiranno
le facce normali a X se il cristallo è sottoposto ad una forza di trazione F in direzione dell'asse Y, fig,11 b. Se sollecitiamo
invece le facce normali ad X a trazione, fig.12 a, ovvero le facce normali ad Y a compressione fig, V.12 b, il cristallo si
deforma in senso contrario di come si era deformato prima, ed anche la polarizzazione che si manifesta nelle facce normali
all'asse elettrico X, risulta di segno contrario.
Reciprocamente, se fra le facce normali all'asse elettrico X, applichiamo una d.d.p., il cristallo subirà una
deformazione analoga a quella accennata. Se si applica una tensione alternata le deformazioni si alternano ed acquistano il
carattere di vibrazioni.
Pag. 6
Elettronica - oscillatori
E' evidente che ogni cristallo tende a vibrare secondo una propria frequenza dipendente dalla forma e dimensioni della lamina e dalla
maniera in cui essa è fissata e sollecitata.
Nel caso di un quarzo libero, di taglio X, la frequenza propria di oscillazione è data dalla formula:
2870
f
d
ove f è espresso in KHz. e d rappresenta lo spessore della lamina in mm. Se la frequenza della tensione elettrica di polarizzazione
risulta uguale a quella di vibrazione propria del cristallo, questi entra in risonanza. 1 cristalli di quarzo di normale uso portano su
ogni faccia uno strato di argento che funziona da elettrodo, e sono sospesi fra due reofori.
Il tutto è contenuto in apposito sostegno custodia di metallo o di resina sintetica, munito di due spinotti, o piedini, per
l'inserimento nel circuito.
I cristalli di quarzo si costruiscono per frequenze variabili da qualche decina di KHz a qualche MHz.
Naturalmente ogni cristallo opera ad una sola frequenza. Per lavorare su frequenze diverse bisogna disporre di altrettanti
quarzi.
6 — Oscillatori a quarzo
Se una piastrina di quarzo viene alimentata da un generatore di tensione, fig.13a, per quanto abbiamo osservato
precedentemente, essa entra in oscillazione generando ai suoi capi una tensione.
Pag. 7
Elettronica - oscillatori
Nel circuito circolerà quindi una corrente la cui ampiezza sarà funzione della frequenza. E' facile verificare che quando il
quarzo entra in risonanza, questa corrente diventa massima. Si ha così una risonanza di corrente per cui il comportamento del quarzo
può essere considerato equivalente a quello di un circuito elettrico risonante ser ie, fig13b, in cui L R C sono gli elementi elettrici
corrispondenti rispettivamente alla massa, all'attrito meccanico interno, all’elasticità del quarzo. Si è posto in parallelo al ramo
risonante serie una capacità Co per tener conto dell'effettiva capacità elettrica costituita dai due elettrodi tra i quali è posto il quarzo.
L'effetto di tale capacità è quello di far risuonare il circuito di fig.13 b su un'altra frequenza fp che è superiore a quella di
risonanza serie fs, risonanza parallela o di tensione. Infatti per f>fs il ramo risonante si comporta induttivamente per cui, quando la
frequenza del generatore è tale che le reattanze dei due rami sono uguali, il circuito entra in risonanza parallelo. Dal circuito di fig.13
b si ricava sia la frequenza di risonanza serie sia la frequenza di risonanza parallelo
fs
1
2
L
C
f
P
(7)
1
1 C
2
1
L
C CO
(8)
confrontando la (8) con la (7) si trova che
fP
C
f S 1
(9)
CO
Dato che C è molto più piccolo di Co la frequenza di risonanza parallelo fp è di poco superiore a quella di risonanza serie fs.
In fig.14 è riportato l'andamento dell'impedenza del quarzo al variare della frequenza. Si osserva come nell'intorno delle due
frequenze di risonanza la curva sia estremamente acuta banda passante molto stretta. Ciò significa che il coefficiente di risonanza
del quarzo è elevatissimo. Esso dipende molto dal taglio delle piastrine e può assumere valori da alcune migliaia ad alcune centinaia
di migliaia di unità.
Valori così elevati del coefficiente di risonanza del quarzo permettono, se esso è usato negli oscillatori, di raggiungere un'alta
stabilità di frequenza delle oscillazioni. Il quarzo come elemento stabilizzatore può essere inserito negli oscillatori in vari modi per cui
si hanno moltissimi oscillatori a quarzo. In fig.15 è riportato lo schema a transistori dell'oscillatore di Pierce. Esso è un oscillatore a
tre punti che sfrutta la capacità base-emettitore Cbe .
Affinché sia verificata la condizione necessaria per le oscillazioni occorre che il quarzo si comporti induttivamente e il circuito
risonante di collettore capacitivamente.
La frequenza di lavoro deve essere pertanto compresa tra la frequenza di risonanza serie e quella di risonanza parallelo e
superiore alla frequenza di risonanza propria del circuito di collettore.
In questa condizione il circuito di fig.15 a si riduce al tipo di Colpitts.
Pag. 8
Elettronica - oscillatori
Pag. 9