oscillatori a tre punti

8.1.4.Oscillatori a tre punti
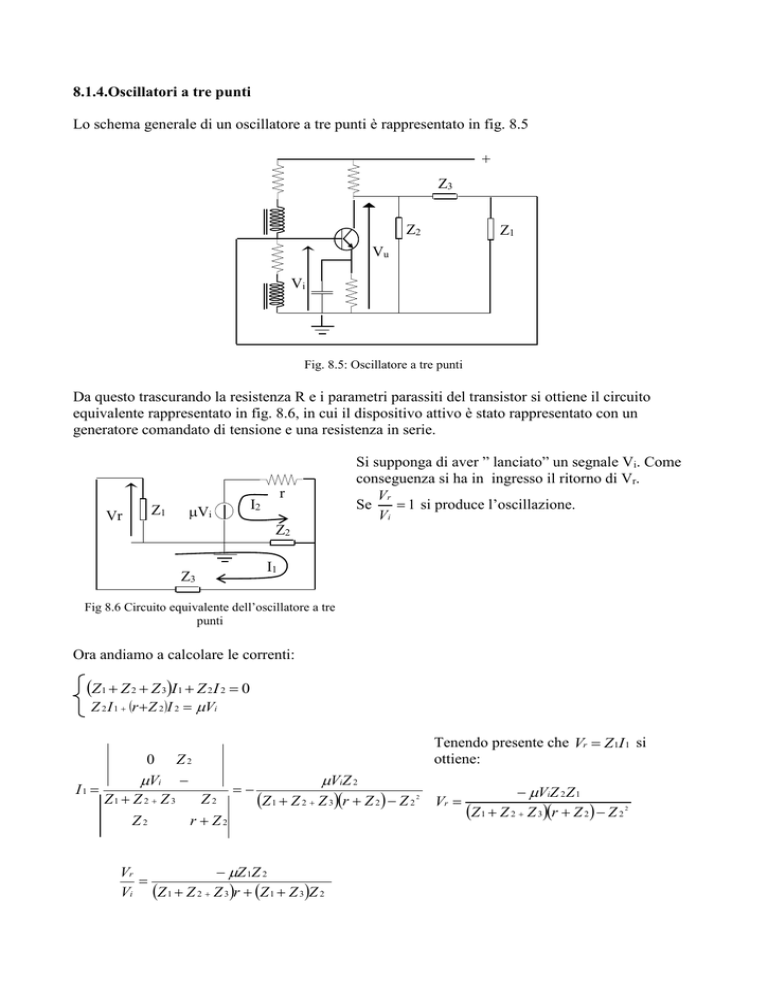
Lo schema generale di un oscillatore a tre punti è rappresentato in fig. 8.5
+
Z3
Z2
Z1
Vu
Vi
Fig. 8.5: Oscillatore a tre punti
Da questo trascurando la resistenza R e i parametri parassiti del transistor si ottiene il circuito
equivalente rappresentato in fig. 8.6, in cui il dispositivo attivo è stato rappresentato con un
generatore comandato di tensione e una resistenza in serie.
Vr
Z1
Vi
r
I2
Si supponga di aver ” lanciato” un segnale Vi. Come
conseguenza si ha in ingresso il ritorno di Vr.
Vr
 1 si produce l’oscillazione.
Se
Vi
Z2
Z3
I1
Fig 8.6 Circuito equivalente dell’oscillatore a tre
punti
Ora andiamo a calcolare le correnti:
Z1  Z 2  Z 3I 1  Z 2 I 2  0
Z 2 I 1  r  Z 2 I 2  Vi
Tenendo presente che Vr  Z1I 1 si
ottiene:
0 Z2
Vi 
ViZ 2
I1 

 ViZ 2 Z 1
Z1  Z 2  Z 3
Z2
Z 1  Z 2  Z 3r  Z 2   Z 2 2 Vr 
Z 1  Z 2  Z 3r  Z 2   Z 2 2
Z2
r  Z2
Vr
 Z 1Z 2

Vi Z 1  Z 2  Z 3r  Z 1  Z 3Z 2
Imponiamo la condizione di realizzare la rete di reazione con reattanze pure:
Vr
 jX 1 jX 2
X 1 X 2


Vi  X 1  X 2  X 3 jr  jX 2 j  X 1  X 3  X 1  X 2  X 3 jr  X 2 X 1  X 3
L’espressione precedente è reale se esiste una frequenza per cui X 1  X 2  X 3  0
Vr
X 1 X 2
 X 1
In questa situazione si impone


1
Vi  X 2 X 1  X 3
 X 1  X 3
X 1  X 2  X 3  0 fornisce la frequenza di oscillazione. Generalmente le reattanze vengono scelte in
base alla seguente tabella di possibili segni (soluzione non unica):
X1
+
-
X2
+
-
X3
+
E la condizione
 X 1
 1 diventa
 X 1  X 3
-X1> X1+ X3
-(+1)X1> X3
-(+1)X1> -( X1+ X2)
X1  X2
Dalla tabella dei segni discendono i due tipi di oscillatori, noti come Colpitts (fig. 8.6) e Hartley
(fig.8.7):
+
+
Z3
Z2
Z2
Z1
Z3
Vu
Vu
Z1
Vi
Vi
Fig 8.6 oscillatorie Colpitts
Fig 8.7 oscillatore Hartley
Osserviamo che un amplificatore selettivo costituito da un BJT con un gruppo LC sul collettore e un
altro gruppo LC in ingresso, a causa della capacità parassita collettore base si presenta molto simile
all’oscillatore Hartley e può diventare instabile.
8.1.5. Oscillatori a quarzo
I quarzi sono utilizzati per ottenere reti di reazione con variazione di fase ripida, quindi utilizzando i
quarzi le reti sono molto stabili. Sulle facce del cristallo del quarzo sono depositati due elettrodi. La
tensione sugli elettrodi induce una deformazione ed una vibrazione meccanica. L’effetto opposto è
la generazione di una tensione elettrica mediante uno stress meccanico. Il circuito risonante
equivalente al quarzo ha un Q altissimo e quindi una curva di fase estremamente ripida. La
frequenza dipende dalla risonanza meccanica, quindi dalla lavorazione che nel caso del quarzo può
essere molto precisa.
R
L
C’
C
Fig.8.8. Simbolo elettrico del quarzo e suo circuito equivalente
In fig. 8.8 è rappresentato il circuito equivalente del quarzo. Il ramo di sinistra traduce le proprietà
meccaniche, mentre la capacità C’ deriva dalle placchette. Il grafico in fig.8.9 dà la reattanza del
circuito. Si vede come siano presenti una risonanza serie e una parallelo. La risonanza serie precede
quella parallelo, ma poiché C’>>C ( circa 100 volte più grande) le due risonanze sono molto
vicine. Si ottiene quindi la variazione estremamente brusca della fase della catena di reazione, che,
come si è visto, è condizione per la precisione nel valore della frequenza di oscillazione.
induttivo
reattanza X
zero
+
risonanza parallelo
f
risonanza serie
capacitivo
Fig.8.9 Oscillatore a quarzo e reattanza della rete di reazione.
Dimostriamo che, se C’>>C , la risonanza è molto prossima alla risonanza parallelo
L’impedenza del circuito di fig.8.8 è data da :
1
Z

1
1
sC
 sC '
 sC '
2
1
s LC  s RC  1
sL 
R
sC
s 2 LC  SRC  1
 3
s LCC ' s 2 RCC ' s(C  C ' )

s 2 LC  SRC  1

sC  sC ' s 2 LC  sRC  1


se R è piccolo l’equazione diventa:

s 2 LC  SRC  1
s 2 LC  1
s 2 LC  1


s 3 LCC ' s 2 RCC ' sC  C ' s 3 LCC ' sC  C ' ss 2 LCC 'C  C '
che per s=j diventa:
1   2 LC
. Si tratta di una reattanza pura, rappresentata nel grafico
j C  C ' 2 LCC '
di fig.8.9.
Si individuano quindi la risonanza parallelo  p 
C  C'
e la risonanza serie  s 
LCC'
1
LC
.
Si vede anche che  p   s .
Infatti
s 
C  C'
C  C'
1
>
. Inoltre, se C’>>C,  p 
è circa uguale (e di poco maggiore) a
LCC '
LCC'
LC
1
.
LC