Prova scritta di Affidabilità dei sistemi e controllo statistico di qualità
18 Febbraio 2016
1. La probabilità di errore nella trasmissione di una cifra binaria attraverso un certo canale di
comunicazione è 10^(-3) .
a) Calcolare la probabilità di totalizzare piu’ di 3 errori trasmettendo un blocco di 1000 bit.
b) Calcolare una approssimazione di tale probabilità usando il teorema del limite centrale.
c) La seguente tabella si riferisce a un campione casuale di 20 ripetizioni della trasmissione di un
blocco di 1000 bit e restituisce il numero di errori verificatosi in ogni trasmissione. Verificare se
il modello probabilistico usato al punto a) si adatta a descrivere il campione casuale mediante
un test di ipotesi:
0 0 3 3 2 1 1 2 0 2 0 1 2 0 0 0 1 0 0 0
d) Immaginando di voler controllare che il processo di trasmissione dei bits è sotto controllo
statistico, costruire una carta di controllo, calcolando direttamente i limiti di controllo.
Soluzione: a) Il numero di errori nella trasmissione di 1000 bit, segue una distribuzione
binomiale di parametro p=10^(-3) e la probabilità da calcolare è ܲሺܺ > 3ሻ = 1 − ܲሺܺ ≤ 3ሻ. In
R, è:
> 1-pbinom(3,1000,10^(-3))
[1] 0.01892683
b) Approssimando la v.a. binomiale con una gaussiana di media np=1 e varianza np(1-p)
> 10^(-3)*1000
[1] 1
> 10^(-3)*1000*(1-10^(-3))
[1] 0.999
> media=10^(-3)*1000
> var=10^(-3)*1000*(1-10^(-3))
si ha ܲሺܺ > 3ሻ = 0.227
> 1-pnorm(3,media,sqrt(var))
[1] 0.02269615
c) Per verificare se il campione casuale segue una distribuzione binomiale di parametri n=1000 e
p=10^(-3), usiamo un test di Kolmogorov-Smirnov:
> ks.test(dati,"pbinom",1000,10^(-3))
One-sample Kolmogorov-Smirnov test
data: dati
D = 0.3677, p-value = 0.008961
alternative hypothesis: two-sided
Il p-value<0.05 pertanto il test rigetta l’ipotesi di distribuzione binomiale.
d) Per costruire la carta di controllo, è necessario il pacchetto qcc. Si ha
> obj<-qcc(dati,1000,type="np")
da cui risulta che il processo è in controllo statistico. I limiti sono: per la linea centrale
> mean(dati)
[1] 0.9
per la linea superiore e inferiore
> media+3*sqrt(media*(1-10^(-3)))
[1] 3.744627
> media-3*sqrt(media*(1-10^(-3)))
[1] -1.944627
In particolare per la linea inferiore essendo negativa, viene usato il valore 0.
2. All’interno di una popolazione, il 15% delle coppie non ha figli, il 20% ne ha uno, il 35% ne ha due e
il 30% ne ha tre. Inoltre, ogni bambino, indipendentemente da tutti gli altri può essere maschio o
femmina con pari probabilità. Si selezioni una famiglia a caso e si denoti con X e Y il numero di
femmine e di maschi prescelti tra i figli in tale famiglia. Costruire la tabella delle probabilità
congiunte.
Soluzione: La probabilità di avere 0 figli è 0.15, che corrisponde a P(X=0,Y=0). La probabilità di
avere 1 figlio, ossia 0.20, va equamente ripartita tra M e F, ossia P(X=0,Y=1)=P(X=1,Y=0)=0.20×0.5.
La probabilità di avere 2 figli, ossia 0.35, contempla il caso (M,M) ossia P(X=0,Y=2), il caso (F,F) ossia
P(X=2,Y=0) e il caso (M,F) e (F,M), ossia P(X=1,Y=1). Poiché (M,M) ha probabilità di occorrenza
0.5^2 così come (F,F), mentre l’evento ‘un figlio maschio e una figlia femmina’ ha probabilità di
occorrenza 2×0.5^2, si ha P(X=0,Y=2)=0.5^2, P(X=1,Y=1)=2×0.5^2, P(X=2,Y=0)=0.5^2. Con lo stesso
ragionamento si completa il caso 3 figli. Le probabilità di avere più di 3 figli sono nulle. La tabella
finale risulta essere
X\Y
0
1
2
3
0
1
2
3
0.15
0.20×0.5
0.35×0.5^2
0.30×0.5^3
0.20×0.5
2×0.35×0.5^2 3×0.30×0.5^2
0
0.35×0.5^2 3×0.30×0.5^2
0
0
0.30×0.5^3
0
0
0
3. I seguenti campioni casuali si riferiscono ai tempi di vita di lampadine prodotte da una azienda in
due periodi distinti dell’anno. Effettuare un confronto statistico tra le due popolazioni.
Primo campione: 0.10 0.83 1.91 0.50 0.59 0.23 0.08 0.03 1.05 0.23 0.29 0.17 0.08
0.40 0.35 0.39 0.48 0.23 0.53 0.46
Secondo campione: 0.21 0.31 0.01 0.44 0.43 0.37 0.26 0.19 0.13 0.04 0.01 0.37 0.02
1.08 0.64 0.44 0.14 0.46 0.28 0.44
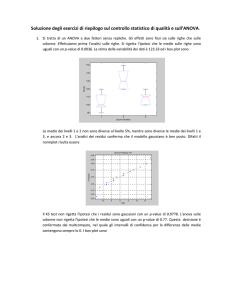
Soluzione: Effettuando un box-plot
si vede che i due campioni appaiono molto simili, fatta eccezione per la presenza di un outlier nel
primo campione , pari a 1.91. Entrambi i campioni non sono gaussiani se gli outliers vengono tenuti
in considerazione:
> shapiro.test(primo)
Shapiro-Wilk normality test
data: primo
W = 0.76737, p-value = 0.000293
> shapiro.test(secondo)
Shapiro-Wilk normality test
data: secondo
W = 0.88172, p-value = 0.019
Guardando alle statistiche
> summary(primo)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0300 0.2150 0.3700 0.4465 0.5075 1.9100
> summary(secondo)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0100 0.1375 0.2950 0.3135 0.4400 1.0800
Il primo campione ha media e mediana maggiori del secondo campione. La variabilità del primo è
maggiore di quella del secondo, ma ciò è dovuto alla presenza di outliers. Tale differenza si riflette
anche nell’ asimmetria e curtosi.
> sd(primo)
[1] 0.4293971
> sd(secondo)
[1] 0.2536528
> skewness(primo)
[1] 1.986535
> skewness(secondo)
[1] 1.16441
> kurtosis(primo)
[1] 4.112372
> kurtosis(secondo)
[1] 1.714969
Con un test di Kolmogorov –Smirnov, stabiliamo che i due campioni provengono dalla medesima
popolazione.
> ks.test(primo,secondo)
Two-sample Kolmogorov-Smirnov test
data: primo and secondo
D = 0.25, p-value = 0.5596
alternative hypothesis: two-sided
Il coefficiente di correlazione è basso
> cor(primo,secondo)
[1] -0.1702661
Per confrontare le medie, usiamo un test non-parametrico .
> wilcox.test(primo,secondo,paired=FALSE)
Wilcoxon rank sum test with continuity correction
data: primo and secondo
W = 239.5, p-value = 0.2912
alternative hypothesis: true location shift is not equal to 0
Le medie sono confrontabili. Gli istogrammi mostrano andamenti con code destre (nel primo è
stato eliminato 1.91).
La legge di Weibull si adatta a entrambe le popolazioni.
> library('MASS')
> fitdistr(primo,'weibull')
shape
scale
1.17500008 0.47407623
(0.19480977) (0.09541632)
> fitdistr(secondo,'weibull')
shape
scale
1.12151982 0.32522610
(0.20774189) (0.06772958)
> fitdistr(c(primo,secondo),'weibull')
shape
scale
1.11785119 0.39567234
(0.13613957) (0.05881855)
> ks.test(c(primo,secondo),'pweibull',1.11785119, 0.39567234)
One-sample Kolmogorov-Smirnov test
data: c(primo, secondo)
D = 0.099964, p-value = 0.819
alternative hypothesis: two-sided
4. Un ricercatore ha organizzato un esperimento fattoriale dove ha valutato l’effetto di 3 tipi di
lavorazione del terreno (lavorazione minima = LM, lavorazione superficiale = SUP, aratura profonda
= PROF) e di due tipi di diserbo chimico (totale=TOT e parziale=PARZ). I dati sono stati raccolti in un
disegno sperimentale fattoriale a blocchi randommizzati.
Effettuare una analisi ANOVA completa.
E’ possibile effettuare una ANOVA a 3 vie, considerando il fattore Blocco. Tuttavia in questo caso
ogni combinazione avrebbe una sola replica, e si perderebbe la significatività statistica. Pertanto è
opportuno effettuare una ANOVA a 2 vie.
> library('HH')
> datianova<-read.table('dati.txt',header=TRUE)
> attach(datianova)
Le medie per combinazioni risultano essere:
> mean(datianova[1:4])
[1] 8.98275
> mean(datianova[5:8])
[1] 5.995
> mean(datianova[9:12])
[1] 9.14125
> mean(datianova[13:16])
[1] 8.47525
> mean(datianova[17:20])
[1] 10.62875
> mean(datianova[21:24])
[1] 9.20675
ossia
Lav\Dis
Min
Sup
Prof
Tot
8.98275
9.14125
10.62875
Parz
5.995
8.47525
9.20675
Dal grafico delle interazioni, risulta che i due fattori interagiscono.
I dati hanno andamento gaussiano:
> shapiro.test(datianova)
Shapiro-Wilk normality test
data: datianova
W = 0.94063, p-value = 0.1684
Per il barlett-test, i gruppi hanno medesima varianza.
> bartlett.test(split(datianova,list(lavorazione,diserbo)))
Bartlett test of homogeneity of variances
data: split(datianova, list(lavorazione, diserbo))
Bartlett's K-squared = 7.5993, df = 5, p-value = 0.1797
Per l’ANOVA si ha
> results<-aov(datianova~lavorazione*diserbo)
> summary(results)
Df Sum Sq Mean Sq F value Pr(>F)
lavorazione
2 23.66 11.828 6.712 0.00664 **
diserbo
1 3.32 3.320 1.884 0.18672
lavorazione:diserbo 2 19.46 9.732 5.523 0.01348 *
Residuals
18 31.72 1.762
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
Dall’analisi risulta che c’è interazione tra lavorazione e diserbo. Pertanto non è possibile validare il
modello. Dal box-plot, le medie risultano significativamente diverse per il fattore lavorazione e per
il fattore blocco.
> boxplot(datianova~lavorazione,col=c('red','blue','pink'),main='Box-plot lavorazione')
> boxplot(datianova~diserbo,col=c('red','blue'),main='Box-plot Diserbo')
Effettuiamo una analisi dei residui. Per il fattore lavorazione
> mediaproflav=mean(datianova[17:24])
> mediaproflav
[1] 9.91775
> mediasuplav=mean(datianova[9:16])
> mediasuplav
[1] 8.80825
> mediaminlav=mean(datianova[1:8])
> mediaminlav
[1] 7.488875
I residui sono gaussiani
> shapiro.test(datianova-mediel)
Shapiro-Wilk normality test
data: datianova - mediel
W = 0.96854, p-value = 0.6312
Analogamente per il fattore diserbo
> mediatotdiserbo=mean(c(datianova[1:4],datianova[9:12],datianova[21:24]))
> mediatotdiserbo
[1] 9.11025
> mediatotdiserbo=mean(c(datianova[5:8],datianova[13:20]))
> mediatotdiserbo
[1] 8.366333
> shapiro.test(datianova-medied)
Shapiro-Wilk normality test
data: datianova - medied
W = 0.9668, p-value = 0.5889