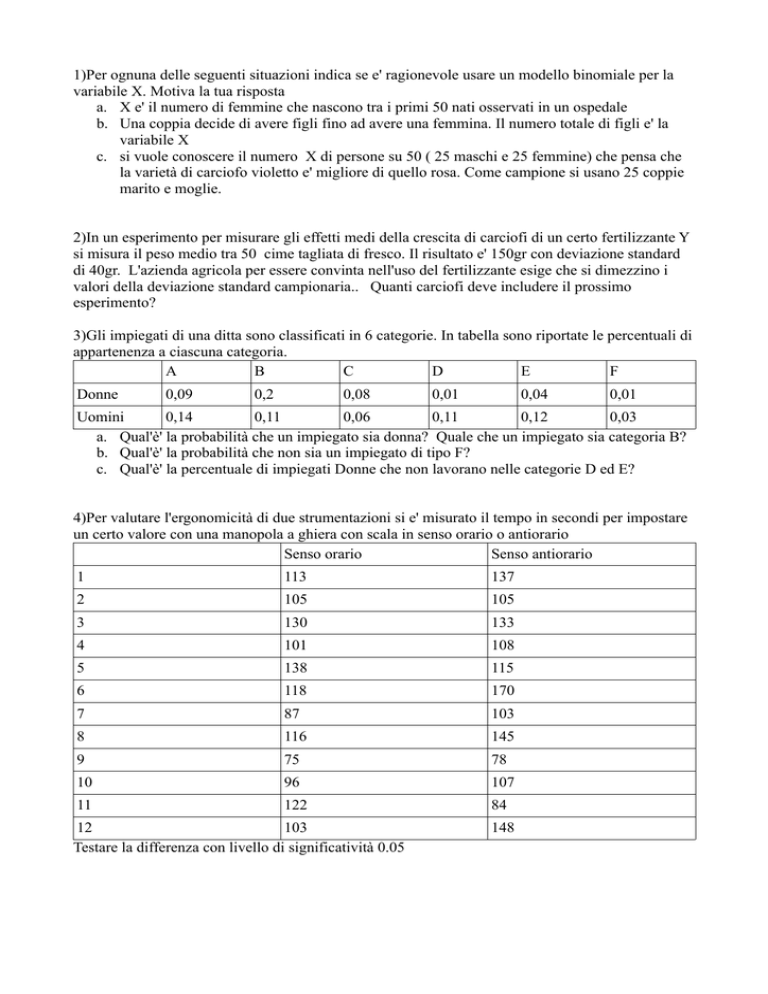
1)Per ognuna delle seguenti situazioni indica se e' ragionevole usare un modello binomiale per la
variabile X. Motiva la tua risposta
a. X e' il numero di femmine che nascono tra i primi 50 nati osservati in un ospedale
b. Una coppia decide di avere figli fino ad avere una femmina. Il numero totale di figli e' la
variabile X
c. si vuole conoscere il numero X di persone su 50 ( 25 maschi e 25 femmine) che pensa che
la varietà di carciofo violetto e' migliore di quello rosa. Come campione si usano 25 coppie
marito e moglie.
2)In un esperimento per misurare gli effetti medi della crescita di carciofi di un certo fertilizzante Y
si misura il peso medio tra 50 cime tagliata di fresco. Il risultato e' 150gr con deviazione standard
di 40gr. L'azienda agricola per essere convinta nell'uso del fertilizzante esige che si dimezzino i
valori della deviazione standard campionaria.. Quanti carciofi deve includere il prossimo
esperimento?
3)Gli impiegati di una ditta sono classificati in 6 categorie. In tabella sono riportate le percentuali di
appartenenza a ciascuna categoria.
A
B
C
D
E
F
Donne
0,09
0,2
0,08
0,01
0,04
0,01
Uomini
0,14
0,11
0,06
0,11
0,12
0,03
a. Qual'è' la probabilità che un impiegato sia donna? Quale che un impiegato sia categoria B?
b. Qual'è' la probabilità che non sia un impiegato di tipo F?
c. Qual'è' la percentuale di impiegati Donne che non lavorano nelle categorie D ed E?
4)Per valutare l'ergonomicità di due strumentazioni si e' misurato il tempo in secondi per impostare
un certo valore con una manopola a ghiera con scala in senso orario o antiorario
Senso orario
Senso antiorario
1
113
137
2
105
105
3
130
133
4
101
108
5
138
115
6
118
170
7
87
103
8
116
145
9
75
78
10
96
107
11
122
84
12
103
Testare la differenza con livello di significatività 0.05
148
5) Per studiare gli effetti dell'insetticida Malathion su un patogeno dell'avena , Oulema melanopus
(Coleottero Crisomelide) sono stati trattati due serie di piccoli appezzamenti uno con le cure
standard e uno con 0.1 kg per ettaro dell'insetticida. Si e' proceduto inseguito a contare le larve
presenti su un fusto per ogni appezzamento. Testare la differenza con livello 0.01
Controllo=2,4,3,4,2,3,3,5,3,2,6,3,4
Trattamento=0,1,1,2,1,2,1,1,2,1,1,1
6) In un esperimento di monitoraggio ambientale ogni ora vengono raccolte in media 2 larve di
Anax imperator (libellula azzurra) per ogni ora e per più di mille campioni di acqua. Per una data
ora:
a. la probabilità di trovarne una o meno
b. la probabilità di trovarne più di una
7)In un ospedale a lunga degenza con durata media di degenza 60 giorni e deviazione standard 15,
assumendo una distribuzione normale, qual'e' la probabilità che una degenza duri :
a. più di 50 giorni
b. tra 30 e 60 giorni
c. meno di 20 giorni
d. più di 90 giorni
8)In una data area metropolitana la probabilità di la media di vincita mensile di gratta e vinci e' 1.
Qual'è la probabilità in un dato mese di avere :
a. nessuna vincita
b. più di una
9)
Risultati di un questionario relativa alla pratica dell'aborto in una data citta'
Zone della città
Favorevole (F)
Contrario (C)
Indeciso (I)
Totale
A
100
20
5
125
B
115
5
5
125
D
50
60
15
125
E
35
50
40
125
135
65
500
Totale
300
Calcola le seguenti probabilità:
P A∩ B
P A∪ B
P C∣D
P B∣I
PF
Risposte:
1)
a. Segue il modello binomiale. C'e' un numero fisso (n=50) di esperimenti di Bernoulli, dunque
con due soli risultati possibili, con la stessa probabilità p di successo.
b. Il numero di esperimenti di Bernoulli non e' fisso dunque il modello binomiale non e'
applicabile
c. Le probabilità p all'interno delle 25 coppie non sono indipendenti tra loro. Infatti le abitudini
alimentari in una coppia sono sicuramente in qualche maniera correlate e dunque non
rappresentano un campione indipendente di 50 individui.
2)Sulla base del Teorema del Limite Centrale la varianza sulla stima della media e' uguale alla
varianza della popolazione diviso la dimensione del campione. Per dimezzare la deviazione
standard che e' la radice quadrata della varianza bisogna quadruplicare la dimensione del campione
e dunque campionare 200 carciofi.
3)
d. Qual'è' la probabilità che un impiegato sia donna? Quale che un impiegato sia categoria B?
La somma della riga donna (0.43), somma colonna B (0.31)
e. Qual'è' la probabilità che non sia un impiegato di tipo F? 1- la somma colonna F
f. Qual'è' la percentuale di impiegati Donne che non lavorano nelle categorie D ed E? 1 – la
somma delle colonne D e E
4)
H0= non c'e differenza fra le due strumentazione come tempo di esecuzione
H1= c'e' differenza nel tempo di esecuzione usando le due strumentazioni.
Livello di significatività del 0.05
Essendo i 12 operatori gli stessi nei due esperimenti ( le unita statistiche sono uguali) devo
utilizzare un t test appaiato.
svolgimento
>A=c(113, 105, 130, 101, 138, 118, 87, 116, 75, 96, 122, 103)
>B=c(137, 105, 133, 108, 115, 170, 103, 145, 78, 107, 84, 148)
>t.test(A,B, pair=TRUE)
Paired t-test
data: A and B
t = -1.458, df = 11, p-value = 0.1728
alternative hypothesis: true difference in means is not equal to 0
conclusione: non si può rifiutare l'ipotesi nulla
5)Test di differenza tra le media con unita statistiche separate e unilaterale. Infatti il risultato atteso
e' che l'insetticida diminuisca il numero degli insetti.
H0=nessuna differenza tra i due gruppi di coltivazioni
H1= il controllo ha più insetti del trattamento
alpha=livello di significatività del 0.01
>Controllo=c(2,4,3,4,2,3,3,5,3,2,6,3,4)
>Trattamento=c(0,1,1,2,1,2,1,1,2,1,1,1)
> t.test(Controllo, Trattamento, alternative='greater',var.equal=TRUE)
Two Sample t-test
data: Controllo and Trattamento
t = 5.834, df = 23, p-value = 3.024e-06
alternative hypothesis: true difference in means is greater than 0
Conclusione : p-value< alpha dunque rifiuto l'ipotesi nulla
6) non si può applicare un modello poissoniano perche il numero di prove non e' fisso ( più di
mille). Si può applicare l'approssimazione poisioniana perche il numero di prove e' alto e la
probabilità di successo di ogni singola prova e' bassa. La domanda ci fornisce direttamente lambda
come media di successi al netto del numero variabile di prove e del scarso successo lambda=2=n*p.
a. 1-ppois(2,2)
[1] 0.3233236
b. > 1-pnorm(50,mean=60,15)
[1] 0.7475075
7)Usando la probabilità cumulativa per una distribuzione normale con media 60 e deviazione
standard 15 si può facilmente stabilire che:
a. 1-pnorm(50,mean=60,15)
[1] 0.7475075
b. > pnorm(60,mean=60,15)-pnorm(30,mean=60,15)
[1] 0.4772499
c. > pnorm(20,mean=60,15)
[1] 0.003830381
d. > 1-pnorm(90,mean=60,15)
[1] 0.02275013
8) Come in esercizio 6 , l'impossibilita di definire un numero di esperimenti fisso, a fronte di un
gran numero di esperimenti tutti con successo molto basso ci permette di usare un modello di
poisson.
a. > ppois(0,1)
[1] 0.3678794
b. > 1-ppois(1,1)
[1] 0.2642411
c. > 1-ppois(3,1)
[1] 0.01898816