Matematica Discreta
Lezione del giorno 1 marzo 2012
Abbiamo definito numero primo un numero intero p>1 che non ha fra i numeri naturali dei divisori
diversi da 1 e p stesso. Un numero intero >1 che non è primo sarà detto numero composto.
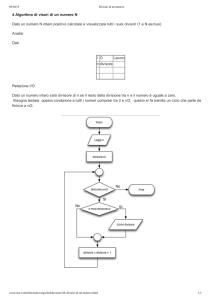
Dato un numero naturale n>1, come verificare se n è un numero primo ?
Possiamo procedere con il seguente algoritmo: elenchiamo i numeri naturali da 2 ad (n-1):
2,3,……,(n-1)
e per ognuno di essi verifichiamo se è un divisore di n (basta dividere n per tale numero e verificare
se il resto è 0). Se in tutte queste divisioni otteniamo sempre resto diverso da 0, concludiamo che
nessuno dei numeri 2,3,….,(n-1) è un divisore di n, dunque n ha solo 1,n come divisori e cioè n è
un numero primo; se invece in almeno una di queste divisioni il resto è 0, allora abbiamo trovato
un divisore di n diverso da 1 e da n, dunque concludiamo che n è un numero composto.
Esempio: il numero n=7 è un numero primo ?
Dividiamo 7 successivamente per 2,3,4,5,6 ottenendo i resti 1,1,3,2,1 che sono tutti diversi da 0, e
concludiamo che 7 ha solo 1,7 come divisori e cioè 7 è un numero primo.
Il numero n=9 è un numero primo ?
Dividiamo 9 successivamente per 2,3,4,5,6,7,8 e ci accorgiamo che dividendo 9 per 3 si ottiene
resto 0, dunque 3 è un divisore di 9 diverso da 1 e 9, ossia 9 è un numero composto.
Tale algoritmo si può rendere più efficiente con la seguente:
Osservazione: se n>1 è un numero composto, fra i numeri 2,3,…..,n-1 il divisore più piccolo di n è
sicuramente non maggiore di n .
Dimostrazione: fra i numeri 2,3,…..,n-1 sia d il divisore più piccolo di n e supponiamo per assurdo
che sia d> n ; essendo d divisore di n, esiste un intero c (sempre fra 2,3,….,n-1) tale che n=cd, e
poiché d è il divisore più piccolo di n, si ha cd, quindi c> n ; ma allora n=cd> n n =n, cioè
n>n, contraddizione.
In base all’Osservazione, basta cercare un eventuale divisore di n fra i numeri 2,3,…..,n-1 che sono
n : se tale divisore esiste, n è composto, altrimenti è primo.
Esempio: il numero n=101 è un numero primo ?
Se adoperassimo l’algoritmo iniziale, dovremmo cercare un eventuale divisore di n fra i numeri
2,3,….,100 (che sono 99), quindi effettuare 99 divisioni.; ma sfruttando l’Osservazione, ci possiamo
limitare ai soli numeri 101 cioè ai numeri 2,3,4,5,6,7,8,9,10 (solo 9 divisioni): poiché tutte le
divisioni di 101 per tali numeri danno resto diverso da 0, concludiamo che n=101 è un numero
primo.
Un criterio di primalità è il seguente: se il numero intero n>1 non ha fra i suoi divisori nessun
numero primo n , allora n è certamente primo.
Dimostrazione: se per assurdo n fosse composto, come visto nell’Osservazione precedente n
avrebbe, fra i numeri 2,3,,,,,,n-1, un divisore d n ; essendo d un intero >1, per il Teorema di
Fattorizzazione Unica d sarebbe prodotto di numeri primi (tutti divisori di d, e tutti n ) ; tutti
questi numeri sarebbero a maggior ragione divisori di n, contraddizione perché per ipotesi n non ha
fra i suoi divisori nessun numero primo n .
In base a tale criterio di primalità, per verificare se un numero intero n>1 è primo potremmo
procedere nel modo seguente: dividere n per tutti i numeri primi n e se tutte le divisioni
avessero resto diverso da 0 potremmo concludere che n è primo.
Esempio: per il numero n=101 esaminato sopra basterebbe dividere 101 per 2,3,5,7 (sono i numeri
primi 101 ) e poiché tutte queste divisioni danno resto diverso da 0 potremmo concludere che
101 è primo (utilizzando solo 4 divisioni invece delle 9 divisioni considerate sopra).
Però per applicare tale criterio di primalità dovremmo avere un elenco completo di tutti i numeri
primi n .
Un tale elenco si può ottenere con il crivello di Eratostene: si scrivono i numeri >1 e n e si
cancellano dapprima i multipli di 2 (4,6,8,10,….); poi si cancellano i numeri multipli del successivo
numero rimasto in elenco (che è 3); così si procede cancellando sempre i numeri multipli del
successivo numero rimasto in elenco. Alla fine nell’elenco restano solo i numeri primi n .
Distribuzione dei numeri primi.
I numeri primi sono distribuiti in modo irregolare nella successione dei numeri naturali: vi sono
zone in cui si “addensano” ed altre in cui sono più “diradati”.
Per esempio, fissato un numero naturale k grande a piacere, è possibile trovare un intervallo di k
numeri naturali consecutivi nel quale non vi sono numeri primi: basta infatti porre n=(k+1)!
(fattoriale di (k+1)) e considerare i k numeri naturali consecutivi seguenti:
n+2, n+3, n+4,…….., n+(k+1)
Nessuno di tali numeri è un numero primo: infatti n=(k+1)! è il prodotto di 1,2,3,…..,k+1, dunque è
divisibile per 2,3,…..,k+1 e allora n+2 è divisibile per 2 (quindi n+2 non è primo), n+3 è divisibile
per 3 (quindi n+3 non è primo) e così via fino a n+(k+1) è divisibile per (k+1) (quindi n+(k+1) non
è primo).
Vi sono coppie di numeri primi molto “vicini” perchè hanno differenza 2 (per esempio 3,5 oppure
5,7 o anche 11,13): sono dette coppie di primi gemelli.
Non è ancora noto se esistono infinite coppie di primi gemelli.
Numeri primi interessanti sono:
2
n
- i numeri primi di Fermat, della forma Fn= 2 1 con n=0,1,2,……
Non tutti i numeri di questa forma sono primi:
F0=3 è primo, e sono primi anche F1=5, F2=17, F3=257, F4=65537, ma F5=4294967297 non è primi
(ha come divisore 641).
Fino ad oggi non sono stati trovati altri numeri primi di questa forma tranne F0,F1,F2,F3,F4 .
- i numeri primi di Mersenne, della forma Mn=2n-1 dove l’esponente n si suppone primo.
Non tutti i numeri di questa forma sono primi:
M2=3 è primo, e sono primi anche M3=7, M5=31, M7=127, ma M11=2047 non è primo (ha come
divisore 23).
Fino ad oggi sono stati trovati 47 numeri primi di questa forma e il più grande di questi ha quasi 13
milioni di cifre in base 10 (vedere il sito http://www.mersenne.org) .
Problema della fattorizzazione in primi.
Dal punto di vista algoritmico nasce il problema seguente:
dato un numero naturale qualunque a, come calcolare i fattori primi della fattorizzazione di a ?.
Un possibile algoritmo è il seguente:
- prima verificare se n è primo (con uno dei metodi esposti sopra, per esempio) perché se n è primo
la sua fattorizzazione è n=n (unico fattore primo n stesso)
- se n non è primo, elencare i primi che sono n , e trovare fra di essi il più piccolo primo
divisore di n (chiamiamolo p, in modo che anche n/p sia un numero naturale e che n=p(n/p))
- osservare che il numero naturale n/p non ha divisori primi <p (se s è divisore primo di n/p allora
n/p=st con t numero naturale, da cui n=pst, dunque s è divisore primo di n, perciò s non è <p perché
p è il più piccolo divisore primo di n)
- elencare i primi che sono p e sono n/p ; se nessuno di questi primi è divisore di n/p,
concludere che n/p è primo, dunque n= p(n/p) è la fattorizzazione di n in prodotto di primi; se
invece uno di questi primi (chiamiamolo q) è divisore di n/p, scrivere n/p=q(n/pq), da cui si ottiene
n= pq (n/pq), e si può proseguire l’algoritmo su n/pq……….
Questo algoritmo (come altri proposti dagli studiosi) non è però molto efficiente. Allo stato attuale
delle ricerche la complessità di calcolo del problema della fattorizzazione è molto più alta rispetto a
quella del problema di verificare se un numero naturale a è primo o no (problema di cui ci siamo
occupati prima): per esempio, anche usando gli algoritmi di fattorizzazione più veloci attualmente
conosciuti, la fattorizzazione in prodotto di primi di un numero naturale con 600 cifre decimali
richiederebbe attualmente 1017 anni (mediamente) di calcolo di un computer che possa eseguire 1
miliardo di istruzioni al secondo.
Cardinalità degli insiemi infiniti.
Se A è un insieme finito (cioè che contiene un numero finito di elementi), abbiamo definito la
cardinalità di A: essa coincide con il numero di elementi di A.
Se volessimo definire il concetto di cardinalità anche per un insieme infinito A, una soluzione
(poco soddisfacente dal punto di vista matematico) potrebbe essere quella di dire semplicemente
che “la cardinalità di un insieme infinito è uguale a infinito”: ciò porterebbe a non distinguere fra i
vari “tipi” di cardinalità infinita.
Cantor propose invece di costruire una teoria per gli insiemi infiniti che fosse coerente con i risultati
validi nel caso degli insiemi finiti.
Ricordiamo un teorema già dimostrato: se A,B sono insiemi finiti e se esiste una funzione biunivoca
f: A B, allora A e B hanno la stessa cardinalità.
L’esistenza o la non esistenza di una funzione biunivoca f: A B, con A,B insiemi infiniti,
potrebbe allora essere presa come definizione dell’eguaglianza o differenza della cardinalità.
Definizione: Se A,B sono insiemi infiniti, diremo che A è equipotente a B (o anche che A,B
hanno la stessa cardinalità) se esiste una funzione biunivoca f: A B (scriveremo in tal caso
AB).
Se esiste una funzione biunivoca f: A B, allora esiste anche la funzione inversa f-1: B A (che è
anch’essa biunivoca), dunque è indifferente dire che A è equipotente a B oppure che B è
equipotente a A.
Il modello più semplice di insieme infinito è l’insieme N dei numeri naturali: diremo che un insieme
infinito A ha la cardinalità del numerabile se A è equipotente ad N, cioè se esiste una funzione
biunivoca f: N A.
Cerchiamo esempi di insiemi numerici infiniti che abbiano la cardinalità del numerabile.
Dimostriamo che: l’insieme Z dei numeri interi relativi ha la cardinalità del numerabile.
Esiste infatti una funzione biunivoca f: N Z, che si può descrivere graficamente (anche se in
modo incompleto) nel modo seguente:
1
2
3
4
5
6
.
.
.
f
0
1
-1
2
-2
3
-3
.
.
.
N
Z
e che formalmente è definita ponendo f(x)=x/2 se x pari, ed f(x)=(1-x)/2 se x è dispari.
Dimostriamo che f è biunivoca.
Iniettività di f: per assurdo siano x,yN, con xy, e tali che f(x)=f(y). Distinguiamo i 3 casi
possibili e in ognuno troviamo una contraddizione:
- x,y entrambi pari: si ha f(x)=x/2=f(y)=y/2, da cui x=y (contraddizione)
- x,y entrambi dispari: si ha f(x)=(1-x)/2=f(y)=(1-y)/2, da cui x=y (contraddizione)
- x,y uno pari (per es. x) ed uno dispari (per es. y): si ha f(x)=x/2=f(y)=(1-y)/2, da cui x=1-y
(contraddizione perché x>0, 1-y≤0).
Surgettività di f: per ogni yZ cerchiamo un xN tale che f(x)=y; se y>0, l’equazione f(x)=x/2=y
ha la soluzione x=2yN; se invece y≤0, l’equazione f(x)=(1-x)/2=y ha la soluzione x=1-2yN
(perché 2y≤0, dunque x=1-2y>0).
Poiché abbiamo costruito una funzione biunivoca f: N Z, possiamo appunto concludere che
l’insieme Z dei numeri interi relativi ha la cardinalità del numerabile.