La rappresentazione dei numeri
interi: i numeri fixed point
Numeri fixed point
z
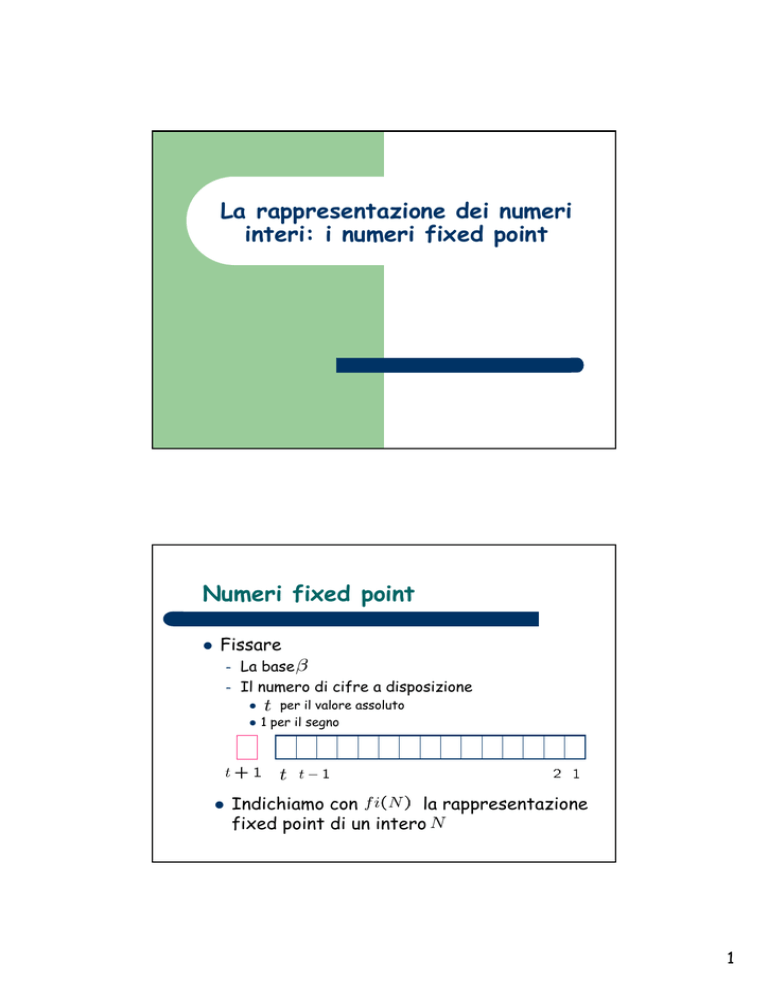
Fissare
–
–
La base
Il numero di cifre a disposizione
z
z
z
per il valore assoluto
1 per il segno
Indichiamo con
la rappresentazione
fixed point di un intero
1
Rappresentazione fixed point di un
intero positivo N
z
A seconda del numero
di cifre della
rappresentazione di N in base
si ha
Esempio: rappresentazione fixed
point di 1235 in base 2 con 16 cifre
2
Se t < p allora fi(N) è il resto della
divisione di N per
z
Esempio
Il più grande intero positivo
rappresentabile esattamente
z
Sono rappresentabili esattamente solo gli
interi positivi compresi nell’intervallo
3
Si richiama la formula
Che si ricava da
Rappresentazione degli interi
negativi
z
z
z
Lavoriamo in base 2.
Complemento a 2 in t+1 cifre
Una regola pratica per ottenere il
complemento a 2 è la seguente:
z Prendere
z Scambiare 1 con 0 e 0 con 1
z Aggiungere 1.
4
Esempio: rappresentazione fixed point
di –1235 in base 2 con 16 cifre
toggle
aggiungi 1
Il primo bit è sempre uguale a 1!
5
Il più piccolo intero negativo
rappresentabile su t+1 cifre in base 2
Infatti si ha
Per valori negativi più piccoli si incorre nell’underflow
intero
L’insieme degli interi
rappresentabili esattamente in
fixed point, base 2, t+1 cifre
z
z
È costituito dagli interi contenuti
nell’intervallo
In generale, se la base è
6
Esempi
Insieme dei numeri fixed point,
base 2, 4 cifre
7
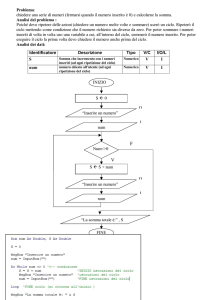
Esercizi
Aritmetica fixed point: somma
8
Aritmetica fixed point: sottrazione
Programma per calcolare il numero
di cifre e il massimo intero
#include <stdio.h>
#include <math.h>
main()
{
int num;
double it,pr;
num=1;
while(num>=0) ++ num;
-- num;
pr=num;
it=log10(pr+1)/log10(2);
printf("max int rappresentabile=\%d cifre=\%lf",num,it+1);
num=-1;
while(num<0)--num;
++num;
printf("min intero rappresentabile=\%d ",num);
}
9
Artimetica fixed point: prodotto
z
z
Siccome il prodotto di due numeri a t+1 cifre
può essere a 2(t+1) cifre, si può incorrere
nell’ overflow intero.
Si esegue con addizioni e scorrimenti a
destra.
Aritmetica fixed point: quoziente
z
Sottrazioni e scorrimenti a sinistra.
10
L’aritmetica fixed point è esatta
purchè si rimanga nell’intervallo di
rappresentazione, cioè a meno di
overflow
11