Istituto Comprensivo “Don Milani”
Via Cambray Digny, 3 – 50136 Firenze
tel.055690743– fax 055690139
e-mail: [email protected] [email protected] [email protected]
Sito web: www.icdonmilani.gov.it
Scuole Primarie “B. da Rovezzano”, “G. E. Nuccio” e “G. Pilati”
Scuole dell’Infanzia “B. da Rovezzano”, “G. E. Nuccio
Scuola Secondaria 1° “Don Milani”
Programma svolto
Docente
Anno scolastico
Barzanti
2014-2015
Materia
Classe
Matematica
II C
MATEMATICA
MISURE, DATI E PREVISIONI:
Presentazione in PowerPoint preparata dall’insegnante
La statistica
Le fasi di un’indagine statistica
Tabelle e grafici statistici: ideogrammi, areogrammi, istogrammi, come costruirli e leggerli
Valori medi e campo di variazione
Moda e mediana
Svolgimento di un’indagine statistica in classe
ARITMETICA
Libro di testo: Rossi G., Con la matematica Aritmetica 2_Edizione Digit, Editore A. Mondadori Scuola
La frazione come numero
Frazioni equivalenti
Semplificazione di una frazione e riduzione ai minimi termini
Le operazioni con le frazioni (addizione, sottrazione, moltiplicazione, divisione e
elevamento a potenza)
Proprietà delle potenze con le frazioni
Espressioni con frazioni
Problemi con le frazioni (diretti, inversi, con la somma e la differenza di due grandezze sapendo che
una è una frazione data dell’altra)
I numeri razionali assoluti (Q)
Frazioni decimali, ordinarie e numeri decimali;
Le operazioni con i numeri decimali finiti
Numeri decimali periodici semplici
Numeri decimali periodici misti
Frazioni generatrici di numeri decimali
Operazioni ed espressioni con i numeri decimali periodici
Confronto tra frazioni e numeri decimali
Valori approssimati dei numeri decimali
I numeri irrazionali assoluti (I)
L’estrazione di radice (come operazione inversa dell’elevamento a potenza)
Quadrati perfetti, radice quadrata e proprietà
Radice quadrata con la fattorizzazione
Approssimazione per difetto
Radice quadrata di un numero decimale e di una frazione
Uso ragionato delle tavole numeriche
Uso della calcolatrice
Radice quadrata di una espressione
Troncamento ed arrotondamento
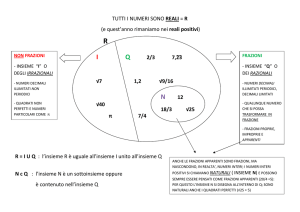
I numeri reali assoluti (R)
Rapporti e proporzioni
Rapporto tra due numeri, diretto ed inverso
Rapporto tra grandezze: omogenee e non omogenee; commensurabili e incommensurabili;
derivate
Le proporzioni e le cinque proprietà
Calcolo del termine incognito
Proporzioni continue
Applicazioni delle proprietà
GEOMETRIA
Libro di testo: Rossi G., Con la matematica Geometria 2_Edizione Digit, Editore A. Mondadori Scuola
I quadrilateri: caratteristiche generali
I trapezi, i parallelogrammi, i rettangoli, i rombi e i quadrati: caratteristiche e classificazione
Attività alla scoperta delle caratteristiche con l’utilizzo di modellini in legno articolabili
Rappresentazione della relazione tra i quadrilateri tramite i diagrammi di Eulero-Venn
Figure equiestese (congruenza, isoperimetria, equivalenza, equiscomponibilità) e misura dell’area
delle superfici
Il calcolo dell’area dei triangoli. Formule dirette ed inverse
La misura dell’area dei quadrilateri: rettangolo, quadrato, parallelogrammo, rombo, quadrilatero
con diagonali perpendicolari, trapezio. Formule dirette ed inverse
Attività laboratoriale con il metodo del ritaglio della carta per la “dimostrazione” delle
formule del calcolo dell’area dei poligoni studiati
Il Teorema di Pitagora
Enunciato diretto e inverso
Dimostrazioni
Attività laboratoriale tratta in parte da MAT@abel “Alla scoperta del Teorema di Pitagora”
Le terne pitagoriche
Attività tratta dalle Chiavi della Città “Evviva la Matematica” che comprende la visita al
Museo della Matematica “Il giardino di Archimede” (Firenze) con un percorso nella sala del
“Teorema di Pitagora” e lo svolgimento dell’attività “La matematica in una bolla di sapone”.
Applicazioni del Teorema di Pitagora al rettangolo, al parallelogramma, al quadrato, al triangolo
isoscele, al triangolo equilatero, al rombo, al trapezio rettangolo, al trapezio isoscele e al triangolo
rettangolo con angoli acuti di 45° e di 30° e 60°
Il piano cartesiano, l’individuazione dei punti e le figure geometriche piane. Calcolo della lunghezza
dei lati di tali figure paralleli agli assi e non (applicazione teorema di Pitagora)
Circonferenza e cerchio
Elementi della circonferenza e del cerchio
Proprietà degli archi e delle corde
Posizione di una retta rispetto alla circonferenza
Posizioni reciproche di due circonferenze
Angoli al centro e alla circonferenza e loro proprietà