9.
Elasticità e onde
Caratteristica di elasticità di un corpo
Facendo riferimento per esempio a una sbarra lunga l, con sezione trasversale A, sollecitata
da una forza F (trazione o compressione) diretta lungo l (e quindi normale ad A), si
definiscono i seguenti parametri:
-
sollecitazione di pressione o trazione = F / A (N/m2)
-
modulo di elasticità longitudinale E del materiale (N/m2)
-
deformazione = l /l (<0 se in compressione e >0 se in trazione)
La legge che descrive la caratteristica lineare o elastica della sollecitazione longitudinale è
= E
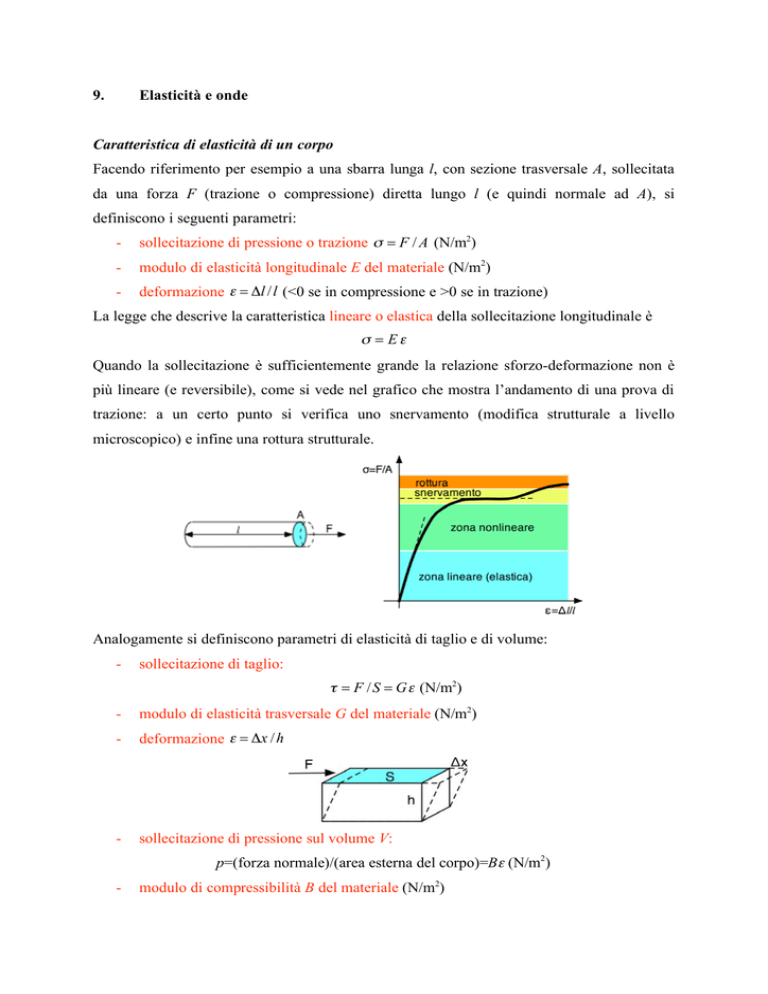
Quando la sollecitazione è sufficientemente grande la relazione sforzo-deformazione non è
più lineare (e reversibile), come si vede nel grafico che mostra l’andamento di una prova di
trazione: a un certo punto si verifica uno snervamento (modifica strutturale a livello
microscopico) e infine una rottura strutturale.
Analogamente si definiscono parametri di elasticità di taglio e di volume:
-
sollecitazione di taglio:
= F /S = G (N/m2)
-
modulo di elasticità trasversale G del materiale (N/m2)
-
deformazione = x /h
-
sollecitazione di pressione sul volume V:
p=(forza normale)/(area esterna del corpo)=B (N/m2)
-
modulo di compressibilità B del materiale (N/m2)
-
deformazione = V /V
Esempio: Calcolare la forza necessaria ad allungare di 1 mm un’asta di acciaio lunga 1 m con
sezione A=1 cm2. (E=2•1011 N/m2)
F = A E l /l = (10-4 m2 2•1011 N/m2 10-3 m)/(1 m)=2•104 N
ossia una forza equivalente al peso di una massa da 2000 kg!
Esempio: Un cubetto d’acciaio di lato a=2 cm lanciato a v0=1 m/s urta elasticamente un’asta
di acciaio di sezione 2x2 cm e lunga 20 cm. Stimare la durata dell’urto e la forza sviluppata
nell’urto, durante il contatto fisico fra cubetto e asta (incastrata ad una parete all’estremità
opposta). (densità acciaio =8000 kg/m3)
I corpi che si deformano elasticamente sono rappresentabili idealmente come una massa
attaccata ad una molla di costante elastica k=AE/l:
F = A E l /l = k x
essendo la deformazione x=l. Notiamo che per due corpi dello stesso materiale e con la
stessa sezione A come in questo esempio, quello più corto è quello più rigido, deformandosi
di una quantità l minore (la forza F si esercita con uguale intensità sui due corpi, per il
principio di azione e reazione). In termini energetici, quasi tutta l’energia elastica di
deformazione viene immagazzinata nell’asta, infatti
1
F2
U = k x2 =
2
2k
essendo il coefficiente k=AE/l dell’asta molto inferiore a quello del cubetto.
Per la conservazione dell’energia, il massimo di deformazione dell’asta si ha verifica quando
tutta l’energia cinetica iniziale è stata convertita in potenziale:
1
1
m v 02 = k x 2
2
2
x=
m
v0
k
essendo k=AE/l=4•108 N/m, m=a30.064 kg. La forza massima che si sviluppa nell’urto è
F = k x = m k v 0 5000 N
La durata dell’urto può essere ragionevolmente stimata come mezzo periodo di oscillazione
della “molla” dell’asta mentre si trova a contatto con il cubetto:
t =
m
=
40 μs
0
k
Durante l’urto, il cubetto di poche decine di grammi produce una forza equivalente ad un
peso di 500 kg (!), in un intervallo di tempo di 40 μs in cui un aereo supersonico si sposta di
2 o 3 cm (!). Questo basta a qualificare “impulsive” le forze intense che si sviluppano negli
urti.
Onde
In tutti i fenomeni ondulatori esiste una sorgente che fornisce energia che si propaga sotto
forma di perturbazione dello stato di un mezzo. Per esempio, un sasso (sorgente) lanciato in
un laghetto converte parte della sua energia meccanica in perturbazione dello stato di quiete
della superficie dell’acqua, originando increspature (onde) che si propagano come cerchi
concentrici rispetto al luogo d’impatto. Un tappo galleggiante, inizialmente a riposo sulla
superficie del laghetto, quando viene investito dall’onda si sposta in su e in giù, acquisendo
energia meccanica che è stata trasportata fin lì dall’onda. Le onde trasportano generalmente
energia, quantità di moto e momento angolare insieme alla variazione di stato del mezzo in
cui si propagano. In generale, invece, non trasportano materia: nell’esempio precedente, se il
sasso è abbastanza piccolo non produce uno spostamento d’acqua verso la riva del lago, ma il
suo effetto è solo quello di modulare la superficie dell’acqua (il tappo si limita ad oscillare in
su e in giù, non viene spinto a riva).
Esempio: onde elastiche
Consideriamo una sbarra di sezione A, allineata ad un righello esterno fermo che identifica la
posizione di tacche marcate sulla sbarra stessa (triangoli blu). Al righello è associato il
sistema di riferimento fisso x. Quando la sbarra è colpita ad un’estremità (per esempio), si
origina un effetto di compressione (sorgente) che si propaga lungo la sbarra stessa sotto
forma di onda, trasmettendo una forza (o quantità di moto) all’altra estremità. La trasmissione
di questo impulso di compressione fa sì che si abbia una deformazione locale nella sbarra che
si propaga, variando la posizione delle tacche marcate rispetto ai corrispondenti segni sul
righello esterno, che si spostano con le linee tratteggiate.
Chiamiamo (x,t) lo spostamento della tacca rispetto alla coordinata x di riferimento,
nell’istante t. Lo stato di deformazione istantaneo della sbarra è definito dalla conoscenza
completa di (x,t) lungo tutta la sbarra. Possiamo usare la legge di Newton applicata ad un
pezzo di sbarra di massa dm, inizialmente a riposo fra le coordinate x e x+dx:
(dm) a = F(x,t) + F(x + dx,t)
Le forze applicate a dm sono di trazione, in quanto convenzionalmente tutti gli incrementi
infinitesimi sono >0, quindi dm si suppone allungata. L’accelerazione di dm va calcolata
come derivata seconda dello spostamento (x,t) di dm. Dipendendo sia dalla posizione di
riposo della tacca sulla sbarra (x) che dall’istante (t) in cui si scatta la foto dello stato di
deformazione, la derivata che si usa è quella di (x,t) rispetto al tempo t, facendo riferimento
ad una posizione x fissa (per questo si chiama derivata parziale):
( A dx)
2 (x,t) [ F(x + dx,t) F(x,t)]
F(x,t)
=
dx =
dx
2
t
dx
x
La forza F è collegata allo stato di deformazione del pezzetto dm mediante la solita
relazione
F = A E = A E
[ (x + dx,t) (x,t)] = A E dx
x
Infine, sostituendo nella legge di Newton precedente:
2 (x,t)
2 (x,t)
=
E
t 2
x 2
che rappresenta l’equazione delle onde (in questo caso onde elastiche longitudinali,
acustiche), e spesso viene presentata nella forma
2 (x,t) 1 2 (x,t)
2
=0
v
x 2
t 2
v=
E
Si noti che v ha le dimensioni di una velocità: è la velocità di propagazione delle onde nella
sbarra. Per l’acciaio è v5 km/s, da confrontare con i 300 m/s del suono in aria!
L’equazione delle onde rappresenta la propagazione di una perturbazione di stato: se la sbarra
è a riposo allora (x,t) =0, cioè le tacche sulla sbarra sono ferme rispetto alle posizioni
corrispondenti sul righello esterno, ma se per esempio si imprime uno stato di deformazione
iniziale (x,0) = u(x) al tempo t=0, questo si propaga lungo la sbarra successivamente, senza
alcun bisogno di intervenire dall’esterno.
Possiamo infatti verificare che entrambe le funzioni “traslate progressivamente lungo l’asse
x” u(x-vt) e u(x+vt) sono soluzioni dell’equazione delle onde, rappresentando rispettivamente
una perturbazione (suono) che si propaga verso destra e verso sinistra:
u(x ± v t) du(s) 2 u(x ± v t) d 2 u(s)
,
=
=
ds
x
ds2
x 2
2
u(x ± v t)
du(s) 2 u(x ± v t)
2 d u(s)
,
= ±v
=
v
ds
t
ds2
t 2
Sostituendo nell’equazione delle onde si vede che essa è soddisfatta, per tutte le funzioni u(s).
Grandezze “propagate” o “trasportate” dall’onda
Nel caso considerato è semplice verificare che le seguenti grandezze fisiche legate alla
perturbazione dello stato di quiete della sbarra sono soluzioni dell’equazione delle onde e
perciò si propagano indistorte lungo la sbarra con velocità v oltre allo spostamento (x,t) :
-
stato di deformazione (x,t) = (x,t) x
-
tensione interna F(x,t) = A E (x,t) x e sforzo F/A
-
quantità di moto per unità di volume, dp /(A dx) = (x,t) t
-
energia meccanica, associata allo stato di deformazione (analogo a quella potenziale
elastica) e cinetica (trasporto di quantità di moto)
Onde armoniche
Sono descritte da semplici funzioni armoniche, seno o coseno, con argomento di due tipi:
(x,t) = 0 sin(k x t) = 0 sin[ k (x v t)]
0 è l’ampiezza dell’onda
la pulsazione angolare
v la solita velocità di propagazione
k = /v è il cosiddetto vettore d’onda
La seconda forma è più simile all’analisi fin qui condotta, e rende più intuitiva la visione
dell’onda che trasla. La prima evidenzia invece il carattere oscillatorio dell’onda armonica:
fissata una posizione x*, lo spostamento dall’equilibrio (x*,t) oscilla con pulsazione
= 2 = 2 /T (ricordando il legame fra pulsazione, periodo e frequenza). Fissato un
istante t*, la fotografia della perturbazione (x,t*) lungo la sbarra è una sinusoide con
periodo spaziale = 2 /k (lunghezza d’onda o distanza fra due picchi adiacenti).
Per le onde armoniche è immediato calcolare la potenza media per unità di area trasportata
dall’onda (detta intensità I):
P
P
T = 2 /
T = 2 /
I=
= F(x,t)v(x,t) = A E
= A E
P
1 t +T
( 0 k) ( 0 )cos2 (k x t) dt
T t
T = 2 /
A
x t
=
1
1
E 02 k = 02 2 v
2
2
Una caratteristica comune a tutti i tipi di onde è il fatto che l’intensità è proporzionale al
quadrato dell’ampiezza del “campo di perturbazione”, alla velocità di propagazione e cresce
con la frequenza.












