La retta nel piano cartesiano

LA RETTA NEL PIANO CARTESIANO
Ogni retta del piano cartesiano è identificata da un’equazione, che si può presentare in diverse forme, tutte
equivalenti tra loro. In particolare, l’equazione di una retta si cerca sempre di rappresentarla in una delle due forme
normali, dette rispettivamente forma esplicita e forma implicita.
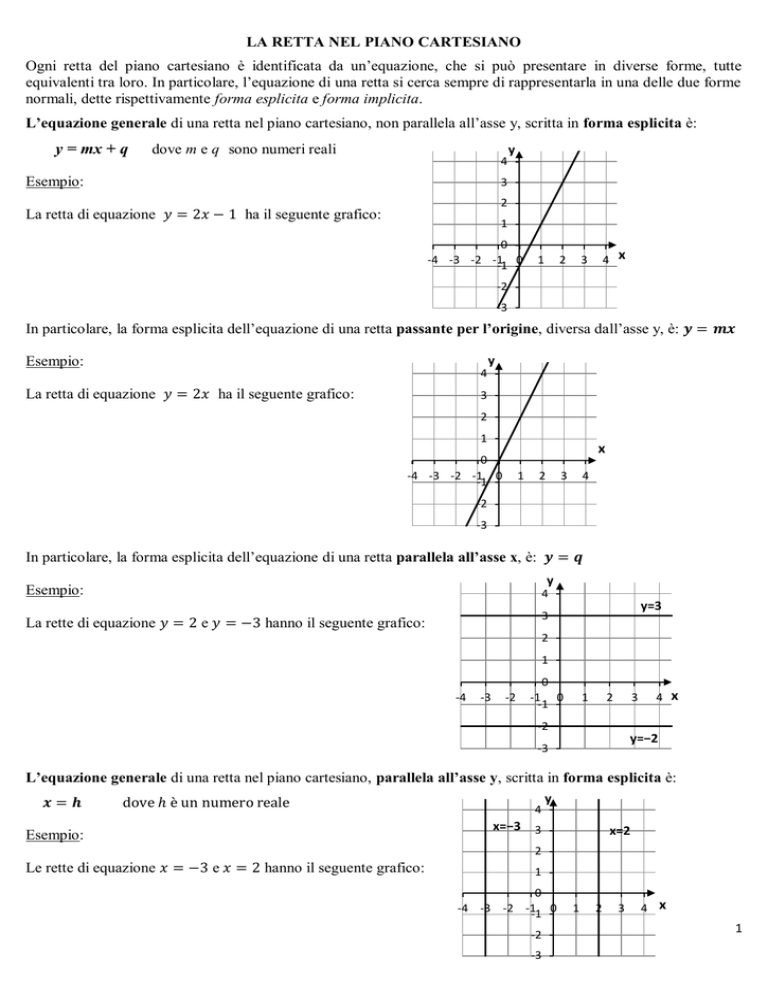
L’equazione generale di una retta nel piano cartesiano, non parallela all’asse y, scritta in forma esplicita è:
y = mx + q
dove m e q sono numeri reali
4
Esempio:
y
3
La retta di equazione
2
ha il seguente grafico:
1
0
-4 -3 -2 -1-1 0
1
2
4 x
3
-2
-3
In particolare, la forma esplicita dell’equazione di una retta passante per l’origine, diversa dall’asse y, è:
y
Esempio:
4
La retta di equazione
ha il seguente grafico:
3
2
1
x
0
-4 -3 -2 -1 0
-1
1
2
3
4
-2
-3
In particolare, la forma esplicita dell’equazione di una retta parallela all’asse x, è:
y
Esempio:
La rette di equazione
4
e
y=3
3
hanno il seguente grafico:
2
1
-4
-3
-2
0
-1 0
-1
1
2
3
-2
4 x
y=−2
-3
L’equazione generale di una retta nel piano cartesiano, parallela all’asse y, scritta in forma esplicita è:
4
y
x=−3 3
Esempio:
x=2
2
Le rette di equazione
e
hanno il seguente grafico:
1
0
-4 -3 -2 -1-1 0
-2
-3
1
2
3
4 x
1
Il significato dei coefficienti m e q
Nell’equazione della retta y = mx + q, il coefficiente m si chiama coefficiente angolare e il coefficiente q termine
noto. Per esempio, nell’equazione:
y = 2x + 3
Il coefficiente
angolare è 2
Il termine
noto è 3
Il termine noto q è l’ordinata del punto d’intersezione della retta di equazione y = mx + q con l’asse y.
y
4
3
2
1
il
termine
noto è 1
(0; 1)
0
-4
-3
-2
-1 0
-1
1
2
3
4
-2
Il coefficiente angolare m dà invece informazioni sulla “inclinazione” della retta rispetto all’asse x: per questo
motivo m viene anche chiamato pendenza della retta.
Se m > 0
La retta y = mx + q forma con l’asse x un angolo
acuto
m>0
percorrendo la retta da
sinistra verso destra si
sale
Se m < 0
La retta y = mx + q forma con l’asse x un angolo
ottuso
m<0
percorrendo la retta da
sinistra verso destra si
scende
angolo
ottuso
angolo
acuto
Se m > 0
al crescere di m le rette y = mx + q formano con
l’asse x angoli acuti di ampiezza via via maggiore;
in altre parole: al crescere di m si ottengono rette
sempre più “ripide”
Se m < 0
al crescere di m le rette y = mx + q formano con
l’asse x angoli ottusi di ampiezza via via maggiore;
in altre parole: al crescere di m si ottengono rette
sempre meno “ripide”
m=2
m = -2
m=1
m = -1
m = 1/2
m = -1/2
2
L’equazione generale di una retta nel piano cartesiano scritta in forma implicita è:
ax + by + c = 0
dove a, b e c sono numeri reali con a e b non entrambi nulli.
Osservazione: la forma implicita ax + by + c = 0 permette di rappresentare tutte le rette del piano, mentre la forma
esplicita y = mx + q non permette di rappresentare tutte le rette del piano cartesiano, in quanto non comprende le
rette parallele all’asse y.
Se l’equazione di una retta è assegnata nella forma ax + by + c = 0 si dice che l’equazione è data in forma
implicita; se invece l’equazione di una retta è assegnata nella forma y = mx + q si dice che l’equazione è data in
forma esplicita.
Per passare dalla forma implicita alla forma esplicita basta risolvere l’equazione implicita rispetto a y.
Esempio: L’equazione 2x + 3y + 2 = 0 è l’equazione di una retta, data i forma implicita. Risolviamo questa
equazione rispetto a y:
2
2
2 x  3 y  2  0  3 y  2 x  2  y   x 
3
3
Abbiamo così ottenuto l’equazione della retta in forma esplicita.
Rette parallele
Due rette non parallele all’asse y, di equazioni y = mx + q e y = m’x + q’, sono parallele se e solo se hanno lo
stesso coefficiente angolare.
La condizione di parallelismo è quindi: m’ = m
Rette perpendicolari
Due rette non parallele agli assi, di equazioni y = mx + q e y = m’x + q’, sono perpendicolari se e solo se i loro
coefficienti angolari hanno prodotto – 1.
La condizione di perpendicolarità è quindi:
1
m  m   1 oppure m'  
m
3
Come determinare l’equazione di una retta
Sappiamo dalla geometria euclidea che una retta resta univocamente individuata quando se ne conoscono un punto
e la direzione, oppure due punti. Trasferendoci nell’ambito della geometria analitica, scaturiscono i seguenti
problemi:
a. determinare l’equazione di una retta passante per due punti assegnati;
b. determinare l’equazione di una retta passante per un punto P(x0,y0) e di coefficiente angolare m assegnato (il
coefficiente angolare individua la direzione della retta).
RETTA PASSANTE PER DUE PUNTI
Si dimostra che, per determinare l’equazione di una retta passante per due punti A(xA, yA) e B(xB, yB) assegnati, con
xA  xB , si può utilizzare la seguente formula:
y  yA 
yB  y A
x  x A 
xB  x A
Si dimostra inoltre, che il coefficiente angolare m della retta passante per A(xA, yA) e B(xB, yB), con xA  xB, è:
m
yB  y A
,
xB  x A
Esempio: Determina l’equazione della retta passante per A(– 2, 4) e B(1, – 1).
y  yA
1 4
5
m AB  B


x B  x A 1   2
3
y4
5
x  (2)
3
ossia
y
5
2
x
3
3
RETTA PASSANTE PER UN PUNTO E PARALLELA A UNA RETTA DATA
Esempio: Determiniamo l’equazione della retta passante per P( – 1; 3 ) e parallela alla retta r, di equazione
x  2y  1  0.
1
1
1
L’equazione della retta r in forma esplicita è: y  x  , quindi il suo coefficiente angolare è m 
2
2
2
In base a quanto scritto prima, è possibile usare la seguente formula
, per cui l’equazione
della retta passante per P( – 1; 3 ) e parallela alla retta r sarà:
1
1
7
y  3  x   1 da cui y  x 
2
2
2
RETTA PASSANTE PER UN PUNTO E PERPENDICOLARE A UNA RETTA DATA
Esempio: Determiniamo l’equazione della retta passante per P( 3; 0 ) e perpendicolare alla retta r, di equazione
y  2x .
Il coefficiente angolare della retta r è 2; pertanto una retta perpendicolare a r deve avere coefficiente angolare
1
1
1
m'     . La retta cercata è allora quella passante per P(3;0) e di coefficiente angolare 
m
2
2
In base alla formula su scritta: y  0  
1
 x  3
2
da cui
y 
1
3
x
2
2
4
5