Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Dimostrazioni
Risoluzione 1)
Ipotesi
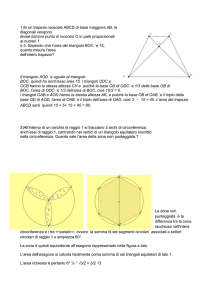
Le circonferenze Γ e Γ' (e Γ'') sono tangenti
P appartiene alla retta tangente comune t
PA, PB (e PB*) sono tangenti
Tesi
PA = PB (= PB*)
Dimostrazione
Non ha importanza se le due circonferenze
sono tangenti esternamente o internamente.
La dimostrazione segue dalla proprietà
transitiva.
Dal teorema delle tangenti ad una
circonferenza condotte da un punto esterno si
ricava che
PA = PT e PB = PT (PB* = PT).
Quindi PA = PB (= PB*)
Risoluzione 2)
Ipotesi
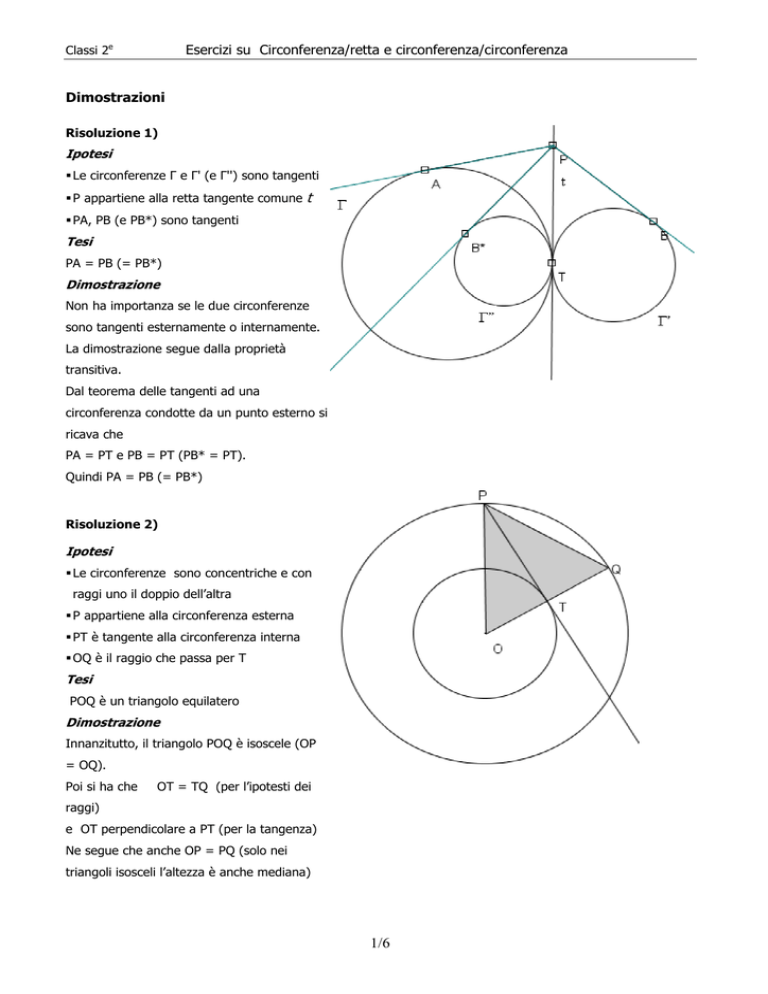
Le circonferenze sono concentriche e con
raggi uno il doppio dell’altra
P appartiene alla circonferenza esterna
PT è tangente alla circonferenza interna
OQ è il raggio che passa per T
Tesi
POQ è un triangolo equilatero
Dimostrazione
Innanzitutto, il triangolo POQ è isoscele (OP
= OQ).
Poi si ha che
OT = TQ (per l’ipotesti dei
raggi)
e OT perpendicolare a PT (per la tangenza)
Ne segue che anche OP = PQ (solo nei
triangoli isosceli l’altezza è anche mediana)
1/6
Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Risoluzione 3)
Ipotesi
Le circonferenze sono concentriche e la
retta AB le interseca.
Tesi
AC = DB
Dimostrazione
Tracciare dal centro la perpendicolare alle
corde.
Per il teorema fondamentale delle corde,
H è punto medio sia di AC che di CD.
La tesi segue per differenza di segmenti
congruenti.
Risoluzione 4)
Ipotesi
le circonferenze sono tangenti
r passa per il punto di tangenza T
r interseca le circonferenze in A e B.
Tesi
AO // BO'
Dimostrazione
La congiungente i due centri passa per T.
I triangoli AOT e BO'T sono isosceli,
hanno gli angoli ‹ATO = ‹BTO' perché
opposti al vertice.
Di conseguenza sono congruenti gli
angoli ‹OAT = ‹TBO' e per il teorema
delle retta parallele AO è parallelo a BO'
(angoli alterni interni congruenti).
Notare che la tesi è vera anche nel caso
che le due circonferenze sono tangenti
internamente (seconda figura).
In questo caso, invece che due angoli
opposti al vertice congruenti) i due
triangoli isosceli hanno un angolo in
comune.
2/6
Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Risoluzione 5)
Ipotesi
le circonferenze sono secanti in A
le circonferenze sono congruenti
O, A e B sono allineati
Tesi
‹BO'C = 3 ‹BOC.
Dimostrazione
Tracciamo il raggio AO’.
Detto
α l’angolo ‹AOO',
la tesi si
ricava trovando, in funzione di
α,
tutti gli angoli dei triangoli AOO' e
AO'B (i quali sono isosceli!).
Risoluzione 6)
Ipotesi
le circonferenze sono secanti nei
punti A e B
AC e AD sono diametri.
Tesi
i punti C, B e D sono allineati.
Dimostrazione
Tracciamo il segmento AB.
Il triangoli ABC è inscritto nella
semirconferenza di diametro AC e
quindi è rettangolo in B.
Analogamente per il triangolo ABD.
L'angolo ‹CBD risulta quindi piatto e i
punti C, B e D risultano dunque
allineati.
3/6
Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Risoluzione 7)
Ipotesi
le circonferenze sono tangenti
le rette r ed s passano per il punto di tangenza T
r interseca le circonferenze in A e B
O1
s interseca le circonferenze in C e D
Tesi
AC // BD
Dimostrazione
Si veda la seconda figura
Congiungendo i centri delle circonferenze con il
punto di tangenza e con gli estremi delle corde si
ottengono sei triangoli isosceli.
Gli angoli di ciascuno dei tre triangoli nella prima
circonferenza sono congruenti agli angoli di
ciascuno dei tre triangoli della seconda
circonferenza.
Per dimostrare ciò, due coppie di triangoli si utilizza
il teorema degli angoli opposti al vertice.
Per dimostrare che ‹CAO1 = ‹O2BD si utilizza il fatto
che ‹AO1C = ‹DO2B per differenza e che gli angoli
alla base dei triangoli isosceli CAO1 e O2BD sono
quindi congruenti, sempre per differenza.
Sommando gli angoli congruenti in A e B, si ricava
che le rette AC e DB formano angoli alterni interni
congruenti se tagliati da r e perciò AC e BD sono
rette parallele.
4/6
Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Risoluzione 8)
Ipotesi
le circonferenze sono tangenti
esternamente nel punto M
MD e ME sono due corde perpendicolari
dalla stessa parte di OO'.
Tesi
DE // OO'
Dimostrazione
Detto
di
α
α l’angolo ‹DMO trovare in funzione
gli angoli dei due triangoli isosceli
DOM e EO’M (tenere presente l’ipotesi che
DME è un angolo retto).
Si ricava che gli angoli ‹DOM e ‹EO’M sono
supplementari e che di conseguenza i raggi
DO e EO' sono paralleli.
Poiché è anche DO = EO' in quanto raggi di
circonferenze congruenti, si ha quindi che il
quadrilatero DOO'E è un parallelogramma
(una coppia di lati opposti congruenti e
paralleli).
Perciò si ha la tesi DE // OO'
Risoluzione 9)
Ipotesi
le circonferenze sono tangenti
esternamente nel punto M
i raggi DO e EO’ sono paralleli e nello
stesso semipiano rispetto OO’.
Tesi
DME è retto
Dimostrazione
Detto
α l’angolo ‹DOM trovare in funzione di α
gli angoli dei due triangoli isosceli DOM e EO’M (tenere
presente l’ipotesi che i raggi sono paralleli e che quindi ‹DOM e ‹EO’M sono supplementari in quanto coniugati
interni.
Dal calcolo si ricava che DME è retto.
5/6
Classi 2e
Esercizi su Circonferenza/retta e circonferenza/circonferenza
Risoluzione 10)
Ipotesi
le circonferenze sono tangenti internamente nel
punto T
la circonferenza interna passa per il centro di quella
esterna.
TB è una semiretta per T
A è l’intersezione di TB con la circonferenza interna
Tesi
A è punto medio di TB
Dimostrazione
Vedere la seconda figura.
Tracciare il diametro TS e le corde OA e SB. Poiché i
triangoli OTA e STB sono inscritti nelle
semicirconferenze, allora sono rettangoli gli angoli
OAT e SBE.
Ne segue che OA e SB sono parallele.
Poiché OT = OS (raggi) per il Teorema di Talete ne
segue che AT = AB.
6/6