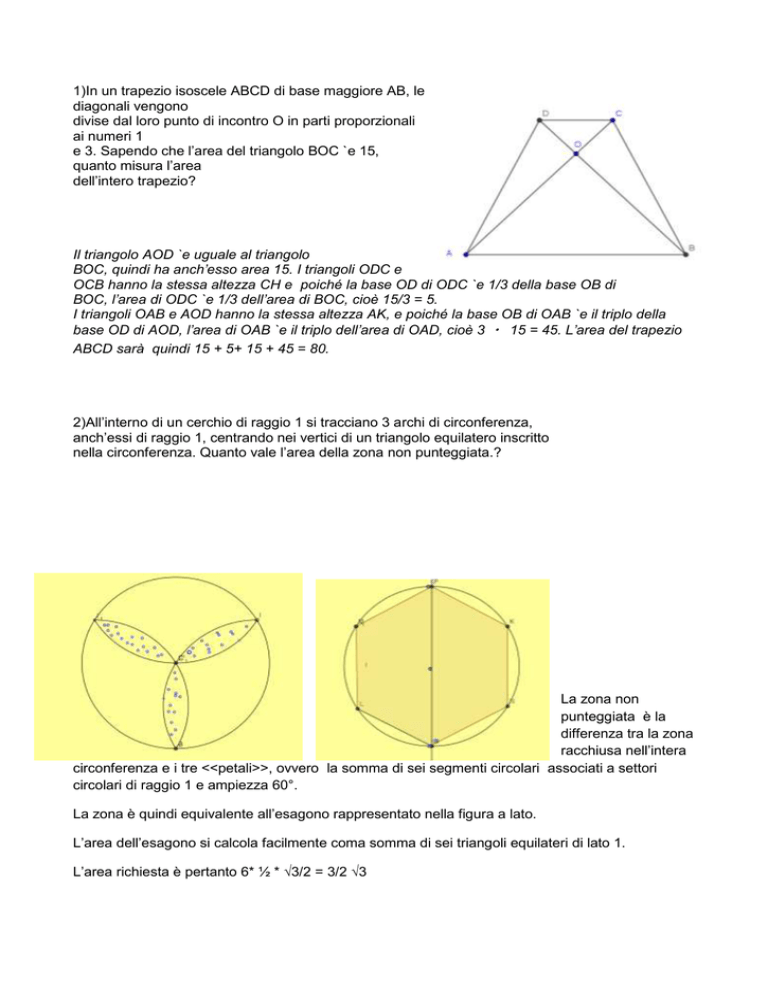
1)In un trapezio isoscele ABCD di base maggiore AB, le
diagonali vengono
divise dal loro punto di incontro O in parti proporzionali
ai numeri 1
e 3. Sapendo che l’area del triangolo BOC `e 15,
quanto misura l’area
dell’intero trapezio?
Il triangolo AOD `e uguale al triangolo
BOC, quindi ha anch’esso area 15. I triangoli ODC e
OCB hanno la stessa altezza CH e poiché la base OD di ODC `e 1/3 della base OB di
BOC, l’area di ODC `e 1/3 dell’area di BOC, cioè 15/3 = 5.
I triangoli OAB e AOD hanno la stessa altezza AK, e poiché la base OB di OAB `e il triplo della
base OD di AOD, l’area di OAB `e il triplo dell’area di OAD, cioè 3 ・ 15 = 45. L’area del trapezio
ABCD sarà quindi 15 + 5+ 15 + 45 = 80.
2)All’interno di un cerchio di raggio 1 si tracciano 3 archi di circonferenza,
anch’essi di raggio 1, centrando nei vertici di un triangolo equilatero inscritto
nella circonferenza. Quanto vale l’area della zona non punteggiata.?
La zona non
punteggiata è la
differenza tra la zona
racchiusa nell’intera
circonferenza e i tre <<petali>>, ovvero la somma di sei segmenti circolari associati a settori
circolari di raggio 1 e ampiezza 60°.
La zona è quindi equivalente all’esagono rappresentato nella figura a lato.
L’area dell’esagono si calcola facilmente coma somma di sei triangoli equilateri di lato 1.
L’area richiesta è pertanto 6* ½ * √3/2 = 3/2 √3
3)Sia AB una corda di una circonferenza e P un punto interno ad
AB tale che AP = 2PB. Sia
DE la corda passante per P e perpendicolare ad AB. Dimostrare
che il punto medio Q di AP `e
l’ortocentro di ADE.
Sia H il punto in cui la retta EQ interseca AD; si deve dimostrare
che l’angolo AbH E `e retto. Tracciamo il segmento BE. Il triangolo
BQE è n isoscele perché l’altezza EP `e anche mediana; infatti P,
piede dell’altezza EP, è punto medio di BQ in quanto PQ
=1/2AP=PB.
EP è pertanto anche bisettrice dell’angolo B EQ, ossia i due angoli P EQ,
P EB sono congruenti. Poi, sono congruenti gli angoli D EB, D AB
perché angoli alla circonferenza che insistono sullo stesso arco; segue che
sono congruenti gli angoli P EQ, D AP. I triangoli AHQ, EPQ hanno
dunque gli angoli in A e in E congruenti; ancora sono congruenti i rispettivi angoli con vertice in Q,
perché opposti al vertice. I triangoli AHQ, EPQ sono pertanto simili e, in particolare, sono
congruenti gli angoli con vertici in P e in H. Poiché l’angolo E PQ `e retto per costruzione,
è retto anche l’angolo AH E, come si voleva dimostrare.
4) In un giorno di sole una sfera è posata su un terreno orizzontale. In un certo istante
l’ombra della sfera raggiunge la distanza di 10 metri dal punto in cui la sfera tocca il terreno. Nello
stesso istante un’asta di lunghezza 1 metro posta verticalmente al terreno getta un’o mbra lunga 2
metri. Qual è il raggio della sfera in metri?
La risposta `e (C). La lunghezza dell’ombra dell’asta ` il doppio della sua altezza quindi AB = ½
BD = 5m. Per il teorema di Pitagora AD = 5√5 m
I triangoli ABD e AEC sono simili per cui
AC : AD = CE: BD.
Posto r = CE si ha:
(5 − r) : 5√5 = r : 10 da cui r = 10√5 − 20.
5)Due triangoli equilateri hanno il baricentro in comune e l’uno si ottiene dall’altro
con una rotazione di 30 gradi. L’area della loro intersezione rappresenta una percentuale dell’area
di uno dei triangoli che è
(A) compresa tra il 50% e il 60%,
(B) compresa tra il 60% e il 70%, (C) compresa tra il 70% e l’80%,
(D) compresa tra l’80% e il 90%,
(E) compresa tra il
90% e il 100%.
La risposta è (C).
I due triangoli in questione sono inscritti in una stessa circonferenza. Indichiamo con r il
raggio e con O il centro di tale circonferenza.
L’area di ciascun triangolo equilatero è uguale
Ovvero, essendo l= r√3
L’area della loro intersezione è pari all’area del triangolo ABC meno l’area di tre
triangoli, tra loro congruenti, ovvero meno tre volte l’area di BLK.
In quest’ultimo si può facilmente osservare che l’angolo in K è retto : infatti, nella rotazione
di 30° intorno ad O, il lato BC , inclinato di 60° sul lato BA, diventerà perpendicolare a
quest’ultimo.
L’area di BLK è data da 1/2BK ·KL dove BK = BH − HK= r/2√3- r/2
e KL =BK√3
Area BLK =
2,
BH = p3
AABC =
2 r,
��������������
��������������
��������������
��������������
��������������
��������������
��������������
��������������
��������������
��������������
��������������
��������������
Di conseguenza l’area dell’intersezione è il rapporto
è
Pertanto l’area dell’intersezione `e il 100(1−(2−√3))%, ovvero il 100(√3−1)%, dell’area di
ABC












