LEZIONE 1
del 10 ottobre 2011
CAPITOLO 1: Numeri naturali
I numeri naturali
N
e numeri interi
Z
sono 0, 1, 2, 3, 4, 5, …
Questi hanno un ordine. Di ogni numero naturale, escluso lo 0, esistono il
precedente ed il successivo.
Si possono rappresentare su una semiretta orientata. Si dice che
è un
insieme discreto perché tra due numeri naturali esistono infiniti altri
numeri non naturali; i numeri naturali sono cioè isolati gli uni dagli altri.
Delle 4 operazioni che conosciamo solo l’addizione e la moltiplicazione
sono operazioni interne ad
: cioè presi due numeri naturali qualunque, il
risultato è ancora un numero naturale. Mentre non sempre esiste in
il
risultato della sottrazione o del quoziente tra due numeri naturali (es:
).
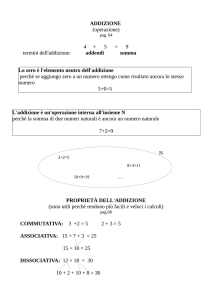
Il numero zero si chiama elemento neutro dell’addizione: sommato a
qualunque intero da l’intero stesso. Attenzione: 0 diviso qualunque numero
da 0, mentre non è possibile la divisione per 0 (es:
non ha
significato).
Il
numero
uno
si
chiama
elemento
neutro
della
moltiplicazione:
moltiplicando un qualunque numero per 1 si ottiene come risultato il
numero stesso.
Un numero naturale è multiplo di un altro se la divisione del primo per il
secondo da come resto 0.
Un numero naturale diverso da 0 è divisore di un altro numero naturale se
la divisione da come resto 0.
Criteri di divisibilità
Un numero è
divisibile per
2
3
5
Quando
L’ultima cifra è pari
oppure zero
La somma delle
cifre è un multiplo
di 3 (cioè 3, 6, 9)
L’ultima cifra è 5
oppure zero
Esempio di
numero divisibile
5679254
Esempio di numero
non divisibile
60018841
74391
7+4+3+9+1=24
2+4=6
279640
310065
32723
3+2+7+2+3=17
1+7=8
9111008
I numeri primi sono quelli che, diversi da 0 ed 1, hanno come divisori
soltanto 1 e se stessi e sono:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ……
Proprietà commutativa : in un’operazione, se si cambia l’ordine degli
addendi, il risultato non cambia
ADDIZIONE:
MOLTIPLICAZIONE:
Proprietà associativa : il risultato di un’operazione non cambia se
s’associano diversamente gli elementi lasciando invariato il loro ordine
ADDIZIONE:
MOLTIPLICAZIONE:
Proprietà distributiva della MOLTIPLICAZIONE rispetto all’addizione:
Proprietà distributiva della DIVISIONE rispetto all’addizione:
Proprietà invariantiva della SOTTRAZIONE: se, in una sottrazione,
aggiungi o togli lo stesso numero sia al minuendo che al sottraendo, la
differenza non cambia:
Proprietà invariantiva della DIVISIONE: se, in una divisione, si moltiplica
o si divide per uno stesso numero, diverso da zero, sia il dividendo che il
divisore, il quoziente non cambia:
Proprietà delle potenze:
Massimo Comun Divisore: di due o più numeri naturali, diversi da zero, è
il più grande fra i divisori comuni (si considera il prodotto dei fattori
comuni, ognuno preso una sola volta, con l’esponente più piccolo)
minimo comune multiplo: di due o più numeri naturali, diversi da zero, è il
più piccolo fra i multipli comuni, diversi da zero (si considera il prodotto
di tutti i fattori primi comuni e non comuni, ognuno preso una sola volta,
con l’esponente più grande.
I numeri interi
sono : … , -4, -3, -2, -1, 0, +1, +2, +3, +4, …
Anche questi numeri hanno un ordine. Di ogni numero intero, esistono il
precedente ed il successivo.
Si possono rappresentare su una semiretta orientata.
Come i naturali, anche gli interi sono un insieme discreto.
Delle
4
operazioni
che
conosciamo,
oltre
all’addizione
moltiplicazione, anche la sottrazione è un’operazione interna a
e
.
alla
Il valore assoluto di un numero è il numero considerato senza il segno che
lo precede:
Esercizi svolti alla lavagna
Pag. 35 n°39
Completa la seguente tabella applicando i criteri di divisibilità:
È divisibile per 2
45
60
171
506
1625
2304
4950
5400
3 5 7 11 13 17 19
X X
X X X
X
X
X
X
X
X
X X
X X X
X
X X X
Quindi:
Pag. 43 n°183
Applica, quando è possibile, le proprietà delle potenze e indica la proprietà applicata:
•
•
•
Pag. 43 n°186
Applica, quando è possibile, le proprietà delle potenze e indica la proprietà applicata:
•
•
•
Esercizi per casa
Assegnati gli esercizi a pag 36 dal n°40 al n°53
Pag. 39 dal 94 al 125
Pag. 42 dal 168 al 179
Pag. 43 dal 183 al 201
Pag.45 dal 221 al 243
Pag. 46 dal 244 al 275
Pag. 50 dal 307 al 321
Pag. 51 dal 332 al 344