Programma di Fisica
Trigonometria essenziale
(Per la scuola superiore)
Autore: Enrico Campanelli
Prima stesura: Giugno 2013
Ultima revisione: Giugno 2013
Per segnalare errori o per osservazioni e suggerimenti di qualsiasi tipo,
potete contattarmi al seguente indirizzo email:
[email protected]
Il titolare dei diritti d’autore di quest’opera è lo studio didattico Studio Bells nella
persona di Enrico Campanelli (www.studiobells.it).
Quest’opera è rilasciata secondo i termini della licenza:
Creative Commons 3.0 Italia
Attribuzione - Non Commerciale - Condividi Allo Stesso Modo
(http://creativecommons.org/licenses/by-nc-sa/3.0/it/)
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
Indice
Premessa
iii
1 Una nuova unità di misura per gli angoli: il radiante
1
2 Tre nuove quantità matematiche
2
2.1
Seno di un angolo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.2
Coseno di un angolo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.3
Tangente di un angolo . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.4
Alcune osservazioni sui valori di seno, coseno e tangente . . . . . . . . . . .
5
2.5
Seno, coseno e tangente come funzioni matematiche . . . . . . . . . . . . .
5
2.6
Angoli negativi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.7
Angoli maggiori di 360◦ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.8
Come si calcolano i valori di seno, coseno e tangente? . . . . . . . . . . . .
9
3 Applicazione ai triangoli rettangoli
10
4 Alcuni esercizi
12
ii
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
Premessa
Questa dispensa è rivolta agli studenti del primo anno di scuola superiore, in particolare
del liceo scientifico, che affrontano per la prima volta lo studio della Fisica. In essa si
introducono in modo semplice ma rigoroso gli elementi basilari di goniometria, ossia
il radiante e le nozioni di seno, coseno e tangente, proposte sia nel senso di funzioni
matematiche, sia nel senso più geometrico di rapporto tra segmenti. Il punto di vista
geometrico è utile per la risoluzione dei triangoli rettangoli e per la scomposizione dei
vettori, argomenti questi, che lo studente incontrerà durante lo svolgimento dei primi
esercizi di cinematica e di dinamica. Poiché lo studio organico della goniometria si fa in
genere negli anni successivi, ma le nozioni di base risultano utili fin dal primo anno, spesso
lo studente proveniente dalla scuola media si trova ‘disarmato’ di fronte ad alcuni problemi
di Fisica, soprattutto se l’insegnante non introduce adeguatamente questi argomenti.
Questa dispensa dovrebbe aiutare lo studente proprio in questa prima fase. Il linguaggio
usato ed i riferimenti nozionistici sono stati scelti in modo da essere adeguati ad uno
studente appena uscito dalla scuola media.
iii
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
(a)
(b)
Figura 1: Misurare gli angoli in radianti.(a) Angolo di ampiezza pari ad un radiante. (b) Elementi
geometrici per il calcolo della misura di un angolo in radianti.
1
Una nuova unità di misura per gli angoli: il radiante
Nella scuola media si è imparato a misurare gli angoli in gradi. Il grado è definito
come la 360-esima parte dell’angolo giro. In questo modo, l’intero angolo giro misura 360◦ ,
l’angolo retto misura 90◦ , l’angolo piatto misura 180◦ e così via. Un’altra unità di misura
per gli angoli è il radiante, e si indica con rad. Il radiante è definito come quell’angolo
che, su una circonferenza centrata nel vertice dell’angolo, individua un arco di lunghezza
ø
pari al raggio. Con riferimento alla figura 1a, nella quale un radiante è rappresentato
dall’area ombreggiata, si ha
AB = OA
(1)
Usando questa nuova unità, la misura di un generico angolo α è data dal rapporto tra la
ø
lunghezza dell’arco di circonferenza individuato dall’angolo, ed il raggio della circonferenza
stessa (vedi figura 1b)
AB
(2)
OA
Vediamo ora quanto misurano in radianti gli angoli più comuni. L’angolo giro, ad esempio,
α=
individua un arco lungo quanto l’intera circonferenza e quindi
angolo giro =
2πOA
= 2π
OA
L’angolo piatto, invece, individua un arco lungo come mezza circonferenza, quindi
angolo retto =
1
2πOA
2
OA
=π
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
L’angolo retto individua un arco pari ad un quarto di circonferenza, per cui
angolo retto =
2πOA
4
OA
=
π
2
Possiamo anche determinare la corrispondenza tra gradi e radianti. Poiché in un angolo
giro di 360◦ , ci sono 2π radianti, per sapere a quanti gradi corrisponde un radiante basta
calcolare
360◦
1 rad =
≈ 57, 3◦ ≈ 57◦ 180
2π
2
(3)
Tre nuove quantità matematiche
Parleremo ora di tre nuove quantità matematiche che hanno a che fare con gli angoli e
sono molto usate nello studio della Fisica. Per descrivere queste nuove quantità è molto
utile rappresentare gli angoli sulla circonferenza trigonometrica, detta anche circonferenza
goniometrica, cioè su una circonferenza con il centro nell’origine di un sistema di assi
Ö
cartesiani, come abbiamo illustrato nella figura 2. In genere la circonferenza trigonometrica
si prende con il raggio pari ad 1, ma per ora conviene considerarla di raggio qualsiasi.
Ö
Ad esempio, nella figura 2, abbiamo rappresentato gli angoli AOP (che chiameremo
per brevità α) e B OP (che chiameremo per brevità β) entrambi con il vertice nell’origine
degli assi ed il primo lato coincidente con il segmento OP . Rappresentando gli angoli
Ö
Ö
in questo modo, si ha che ad ogni angolo possiamo associare il punto sulla circonferenza
trigonometrica coincidente con l’estremità del secondo lato. Ad esempio, all’angolo AOP
resta associato il punto A, all’angolo B OP resta associato il punto B e così via.
2.1
Seno di un angolo
La prima nuova quantità di cui parleremo si chiama seno ed è sempre riferita ad un
angolo. Per indicare, ad esempio, il seno di un dato angolo γ, scriveremo
sin γ
e si leggerà seno di gamma.
Il seno di un qualsiasi angolo γ è definito come il seguente rapporto
2
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
Figura 2: La circonferenza trigonometrica..
sin γ =
coordinata y del punto della circonferenza trigonometrica associato all’angolo γ
raggio della circonferenza trigonometrica
(4)
Ad esempio, per gli angoli α e β di figura 2 avremo che
sin α =
2.2
Ay
;
OP
sin β =
By
OP
(5)
Coseno di un angolo
L’altra quantità importante si chiama coseno ed è anch’essa sempre riferita ad un
angolo. Per indicare, ad esempio, il coseno di un dato angolo γ, scriveremo
cos γ
e si leggerà coseno di gamma.
Il coseno di un qualsiasi angolo γ è definito come il seguente rapporto
3
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
cos γ =
coordinata x del punto della circonferenza trigonometrica associato all’angolo γ
raggio della circonferenza trigonometrica
(6)
Ad esempio, per gli angoli α e β di figura 2, avremo che
Ax
;
OP
cos α =
2.3
cos β =
Bx
OP
(7)
Tangente di un angolo
La terza quantità importante si chiama tangente ed è anch’essa sempre riferita ad un
angolo. Per indicare, ad esempio, la tangente di un dato angolo γ, scriveremo
tan γ
e si leggerà tangente di gamma.
La tangente di un qualsiasi angolo γ è definita come il seguente rapporto
tan γ =
coordinata y del punto della circonferenza trigonometrica associato all’angolo γ
coordinata x del punto della circonferenza trigonometrica associato all’angolo
(8)
Per i nostri soliti angoli α e β di figura 2, avremo quindi che
tan α =
Ay
;
Ax
tan β =
By
Bx
(9)
Ora osserviamo che la tangente di un angolo corrisponde al rapporto tra il seno ed il
coseno di quell’angolo e cioè
tan γ =
sin γ
cos γ
(10)
Per vedere che il rapporto tra il seno ed il coseno di un angolo è proprio uguale alla
tangente di quell’angolo, prendiamo per esempio l’angolo α e consideriamo la prima delle
equazioni (5) e la prima delle equazioni (7). Si trova subito che
4
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
sin α
=
cos α
Ay
OP
Ax
OP
=
Ay
Ay OP
·
=
Ax
OP Ax
(11)
che coincide proprio con il valore di tan α dato nell’equazione (9).
2.4
Alcune osservazioni sui valori di seno, coseno e tangente
Dalle definizioni di seno, coseno e tangente, è facile dedurre che:
• i valori del seno, del coseno e della tangente di un angolo possono essere sia positivi
che negativi. Ciò si vede facilmente considerando che, riferendosi alla figura 2, il
segno delle coordinate dei punti A e B può essere sia positivo che negativo. Ad
esempio sin α è positivo perché Ay è positiva, mentre cos β è negativo perché Bx è
negativa;
• i valori del seno e del coseno di un angolo sono sempre compresi tra −1 e +1. Questo
dipende dal fatto che, ad esempio, il modulo delle coordinate del punto A non può
mai essere superiore al valore del raggio della circonferenza, e quindi il loro rapporto
è sempre minore o uguale ad 1;
• i valori della tangente, a differenza di quelli del seno e del coseno, non sono limitati
tra −1 e +1 ma possono essere qualsiasi;
• per gli angoli di 0◦ e di 90◦ , i valori del seno e del coseno si ricavano facilmente
osservando la figura 2:
– se fosse α = 0◦ , si avrebbe Ay = 0 e quindi sin 0◦ = 0; inoltre si avrebbe
Ax = OP e quindi cos 0◦ = 1
– se fosse α = 90◦ , si avrebbe invece Ay = OP e quindi sin 90◦ = 1; inoltre si
avrebbe Ax = 0 e quindi cos 90◦ = 0
2.5
Seno, coseno e tangente come funzioni matematiche
Durante la scuola media, probabilmente si è già incontrato il concetto di funzione
matematica. Detto molto semplicemente, una funzione matematica è una ‘formula’ tramite
5
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
la quale ad ogni valore di una variabile, se ne associa uno di un’altra variabile. Ad esempio,
una funzione matematica è la formula
y = 3x2
(12)
tramite la quale ad ogni valore della variabile x si associa il valore della variabile y ottenuto
sostituendo al posto della x il suo valore numerico. Ad esempio, al valore x = 2 si associa
il valore y = 3 · 22 = 12, al valore x = 5 si associa il valore y = 3 · 52 = 75 e così via. Un
semplice tipo di funzione matematica che si è certamente visto in terza media è l’equazione
di una retta, come ad esempio
y = 2x + 1
(13)
Tramite questa funzione, data la coordinata x di un punto P che si trova sulla retta, si può
calcolare il corrispondente valore della coordinata y del punto P . La retta rappresentata
dalla funzione y = 2x + 1 si chiama grafico della funzione, ed è composta da tutti i punti
del piano cartesiano la cui coordinata y si ricava dalla coordinata x tramite la formula
espressa dalla funzione.
Anche il seno, il coseno e la tangente di un angolo possono essere visti come funzioni.
Se scriviamo ad esempio
y = sin x
(14)
diciamo che essa è la funzione che ad ogni valore dell’angolo x, associa il valore y dato dal
seno dell’angolo x. Analogamente, si possono considerare le altre due funzioni
y = cos x
y = tan x
(15)
Queste funzioni si chiamano funzioni goniometriche o anche funzioni trigonometriche.
Nella figura 3 sono riportati i grafici delle tre funzioni goniometriche che, ovviamente,
non sono delle linee rette ma sono linee curve. I grafici delle funzioni seno e coseno, in
particolare, hanno una forma che ricorda le onde del mare e, come già osservato, si vede
che i valori di queste due funzioni oscillano sempre tra −1 ed 1.
6
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
(a) Grafico della funzione y = sin x.
(b) Grafico della funzione y = cos x.
(c) Grafico della funzione y = tan x.
Figura 3: Grafici delle principali funzioni goniometriche.
2.6
Angoli negativi
Si sarà notato che i grafici in figura 3 sono disegnati anche per valori negativi dell’angolo
x: ma che significato ha un angolo negativo? Per capirlo, ritorniamo ancora sulla figura 2
della circonferenza trigonometrica. Come si vede, su di essa abbiamo rappresentato gli
angoli α e β orientati in verso antiorario, ma è possibile anche orientare gli angoli in verso
orario. Per i segni, vale la seguente regola: gli angoli orientati in verso antiorario vengono
considerati positivi, mentre quelli orientati in verso orario vengono considerati negativi.
Ad esempio, nella figura 4a, abbiamo disegnato un angolo positivo α = 60◦ ed un angolo
negativo β = −45◦ . Per determinare il valore delle funzioni goniometriche per gli angoli
negativi, si procede normalmente usando le stesse definizioni viste prima, e cioè dobbiamo
considerare le coordinate del punto della circonferenza associato all’angolo ed usare le
formule (4) e (6).
Osserviamo, infine, che può accadere che un angolo positivo ed uno negativo abbiano
lo stesso punto associato; in questo caso, le coordinate del punto associato sono le stesse
7
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
(a) Angoli negativi.
(b) Angoli diversi con stesso punto associato.
Figura 4: Angoli positivi e negativi.
per entrambi gli angoli e quindi per essi le funzioni goniometriche assumeranno gli stessi
valori. Ad esempio, è facile vedere dalla figura 4b che un angolo positivo α = 315◦ ed un
angolo negativo β = −45◦ hanno lo stesso punto associato C.
2.7
Angoli maggiori di 360◦
Si sarà anche notato che i grafici sono disegnati anche per valori dell’angolo x che
superano il valore 2π e cioè 360◦ : ma che significato ha un angolo maggiore di 360◦ ? Per
capirlo, guardiamo ancora la figura 2 della circonferenza trigonometrica. Se immaginiamo
di disegnare un angolo che diventa sempre più grande, dopo aver superato il valore
di 360◦ si vede che il punto associato all’angolo ricomincia a percorrere un nuovo giro
sulla circonferenza trigonometrica, ritornando sulle stesse posizioni del giro precedente.
Ad esempio, se disegnamo un angolo di 390◦ , si vede che il punto associato all’angolo
andrà ad occupare la stessa posizione del punto associato ad un angolo di 30◦ (infatti
390◦ = 360◦ + 30◦ ), ed un angolo di 450◦ è equivalente ad un angolo di 90◦ (infatti
450◦ = 360◦ + 90◦ ). In generale, ogni volta che il valore di x supera un multiplo di 360◦ , i
valori delle funzioni goniometriche si ripetono uguali. Questa proprietà si esprime dicendo
che le funzioni goniometriche sono funzioni periodiche di periodo pari a 360◦ .
8
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
Tabella 1: Valori delle funzioni seno e coseno per alcuni angoli notevoli.
2.8
α (◦ )
α (rad)
sin α
0◦
0
0
30◦
π
6
45◦
π
4
60◦
π
3
90◦
π
2
1
2
√
2
2
√
3
2
1
√
cos α
1
√
3
2
√
2
2
1
2
0
120◦
2
π
3
135◦
3
π
4
3
2
√
2
2
150◦
5
π
6
1
2
2
2
√
− 23
180◦
π
0
−1
− 12
√
−
Come si calcolano i valori di seno, coseno e tangente?
A questo punto ci si chiederà come si fa in pratica a calcolare il seno di un angolo e
cioè quali calcoli bisogna fare sul valore di un angolo per ricavarne il seno. La risposta
è semplice: non è possibile calcolare il seno o il coseno di un angolo tramite addizioni,
sottrazioni, moltiplicazioni o divisioni da eseguire sul valore dell’angolo, e quindi tali valori
vanno calcolati direttamente a partire dalla circonferenza trigonometrica e misurando con
il righello i valori delle coordinate del punto associato ad un angolo e la lunghezza del
raggio. Per fortuna, tutto questo lavoro è già stato fatto da qualcuno ed i risultati sono
stati inseriti nelle tavole numeriche e nelle memorie delle calcolatrici.
Nella tabella 1 sono riportati i valori delle funzioni seno e coseno per alcuni importanti
valori dell’angolo (nella tabella gli angoli sono espressi sia in gradi che in radianti).
Ricordiamo che i valori della funzione tangente possono essere ricavati semplicemente
facendo il rapporto tra i valori del seno e del coseno. Ad esempio, per un angolo di 30◦
(ossia di
π
6
rad), si ha
tan
sin π6
π
=
=
6
cos π6
1
√2
3
2
9
=
1 2
1
·√ =√
2
3
3
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
Se usiamo la calcolatrice, poiché gli angoli si possono misurare sia in gradi che in
radianti, bisogna prima impostarla nella modalità giusta, e cioè nel ‘modo gradi’ se
inseriamo il valore dell’angolo in gradi, oppure nel ‘modo radianti’ se usiamo i radianti.
Tale impostazione si fa tramite il tasto ‘MODE’ presente sulla calcoltrice (i dettagli su
come si fa dipendono dal modello di calcolatrice) e la modalità in cui si trova la calcolatrice
è indicata dalla scritta ‘DEG’ (per il ‘modo gradi’) o ‘RAD’ (per il ‘modo radianti’) che
compare nella parte bassa o alta del display.
Se ad esempio vogliamo calcolare sin 30◦ , dobbiamo prima impostare la calcoltrice nel
‘modo gradi’, poi scrivere 30 e poi premere il tasto SIN (oppure, a seconda del modello di
calcolatrice, prima premere il tasto SIN e poi scrivere 30) ed otterremo il risultato
sin 30◦ = 0, 5
Se invece vogliamo fare lo stesso calcolo usando i radianti, osserviamo innanzi tutto che
30◦ corrispondono a
π
6
radianti e cioè a circa 0, 5236 radianti. Impostiamo poi la calcoltrice
nel ‘modo radianti’, eseguiamo il calcolo inserendo il valore in radianti ed otteniamo
sin 0, 5236 = 0, 5
Come si vede, il valore che si ottiene per il seno è ovviamente sempre lo stesso, indipendentemente dall’unità di misura usata. I tasti da usare per le altre due funzioni goniometriche
sono COS per il coseno e TAN per la tangente.
3
Applicazione ai triangoli rettangoli
Una applicazione molto utile delle funzioni goniometriche è quella ai triangoli rettangoli.
Riferiamoci ancora alla figura 2 e consideriamo il triangolo rettangolo OAx A, che ha per
ipotenusa il segmento OA e per cateti i segmenti OAx e Ax A (ricordiamo che Ax è la
coordinata x del punto A ma qui abbiamo usato il simbolo Ax per indicare anche la
proiezione del punto A sull’asse x). Se invertiamo le prime equazioni delle (5) e delle (7),
si trova subito che
Ay = OA sin α
Ax = OA cos α
10
(16)
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
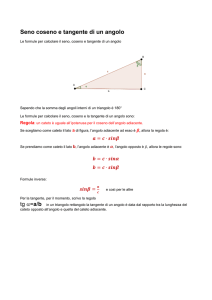
Figura 5: Relazioni tra le funzioni seno e coseno e gli elementi di un triangolo rettangolo.
Guardando la figura 2, si vede che il valore di Ay corrisponde alla lunghezza del cateto Ax A
e cioè del cateto opposto all’angolo α, mentre il valore di Ax corrisponde alla lunghezza
del cateto OAx e cioè del cateto adiacente all’angolo α. Possiamo quindi ricavare queste
due importantissime regole, valide per i triangoli rettangoli:
• il cateto opposto ad un angolo acuto è uguale al prodotto dell’ipotenusa per il seno
dell’angolo
• il cateto adiacente ad un angolo acuto è uguale al prodotto dell’ipotenusa per il coseno
dell’angolo
Per aiutare la memoria a ricordare queste due importantissime relazioni, e cioè per
ricordarci che per il cateto opposto ci vuole il seno e per il cateto adiacente ci vuole il
coseno, possiamo sostituire il termine adiacente con il termine accostato, poiché esso ci
ricorda la parola coseno. Possiamo quindi scrivere:
cateto opposto = ipotenusa · sin α,
(17)
cateto acCOStato = ipotenusa · cos α
(18)
La figura 5 può aiutare ulteriormente a imprimere nella mente queste relazioni. In
essa abbiamo indicato con a l’ipotenusa e abbiamo mostrato entrambi gli angoli acuti.
Notiamo come un cateto possa essere calcolato usando la funzione seno oppure la funzione
coseno a seconda che si usi un angolo acuto oppure l’altro.
11
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
C
L
LV
α
A
B
LO
Figura 6: La salita e gli spostamenti orizzontale e verticale possono essere rappresentati tramite i
lati di un triangolo rettangolo.
4
Alcuni esercizi
Mostreremo ora alcune importanti applicazioni delle formule viste qui sopra.
Esercizio
Una salita ha una pendenza di α = 30◦ rispetto all’orizzontale ed è lunga L = 10 m.
Calcolare di quanto si sposta in orizzontale ed in verticale un’auto che percorre l’intera
salita.
Soluzione
In figura 6 è rappresentata schematicamente la salita. Si vede subito che il problema si
descrive bene tramite un triangolo rettangolo la cui ipotenusa è la salita ed i cui cateti
sono gli spostamenti richiesti dal problema. Lo spostamento orizzontale LO corrisponde al
segmento AB, che è il cateto ‘accostato’ all’angolo α, e quindi si trova subito (usando i
valori della tabella 1)
√
√
√
3
3
LO = L cos α = L
= 10
= 5 3 = 8, 66 m
2
2
Lo spostamento verticale LV corrisponde invece al segmento BC che, essendo il cateto
‘opposto’ all’angolo α, richiede la funzione seno
1
1
LV = L sin α = L = 10 = 5 m
2
2
12
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
~
R
F~2
α
F~1
~ possono essere rappresentate tramite i lati di
Figura 7: Le forze F~1 ed F~2 e la loro risultante R
un triangolo rettangolo.
Esercizio
La forza F~1 (orizzontale) di intensità F1 = 15 N e la forza F~2 (verticale) hanno per
~ che forma un angolo α = 60◦ rispetto all’orizzontale. Calcolare
risultante la forza R
~ e di F~2 .
l’intensità di R
Soluzione
~ ottenuta con il
In figura 7 sono rappresentate le forze F~1 ed F~2 e la loro risultante R
metodo punta-coda. Si vede subito che il problema si descrive bene tramite un triangolo
~ ed i cui cateti sono F~1 ed F~2 . Poiché F~1 è il cateto ‘accostato’
rettangolo la cui ipotenusa è R
all’angolo α, si ha che
F1 = R cos α
Da questa equazione, possiamo ora ricavare facilmente R (dividiamo entrambi i membri
per cos α)
R=
F1
F1
15
=
= 1 = 15 · 2 = 30 N
◦
cos α
cos 60
2
Ora che conosciamo R, possiamo ricavare F2 osservando che essa è il cateto opposto
all’angolo α e quindi
√
F2 = R sin α = R sin 60◦ = 30
13
√
3
= 15 3 = 25, 98 N
2