Curiosità matematiche nella vita quotidiana I legami tra natura e

Curiosità matematiche nella vita quotidiana
I legami tra natura e matematica
Una delle sfide più entusiasmanti di tutte le età è quella di
trovare un quadrifoglio, ritenuto un grande portafortuna: questa
ricerca però, in realtà è sempre fonte di delusione. È ragionevole
pensare che da qualche parte vi sia un quadrifoglio, quindi perché
la natura è così avara di quadrifogli? Osservando i fiori si nota
che la maggior parte di essi è composta da cinque petali, numero
che ritorna anche nella disposizione dei semi: è possibile
osservarlo tagliando una mela al suo “equatore”, notando che i
semi sono sistemati all‛interno di una bella stella a cinque punte.
Nel mondo vegetale prevalgono quindi i numeri dispari, mentre in
quello animale i pari (le zampe sono sempre pari). Un‛indagine più
accurata rivela che anche altri numeri sono piuttosto ricorrenti
tra le piante: esaminando un ananas o una pigna si nota che hanno
file spiraliformi che si susseguono dalla cima alla base, l‛una in
senso opposto all‛altra. Di solito queste file in un ananas sono 8 e
13, mentre in una pigna 13 e 21 o 21 e 34. Anche nei girasoli si
possono individuare spire di semi che vanno dal centro all‛esterno
in senso orario e antiorario, il loro numero è solitamente di 34 e
55 o 55 e 89. I numeri 8, 13, 21, 34 e 55 sono i più comuni: non è
un caso, esiste un legame profondo tra natura e matematica,
natura e i numeri di Fibonacci.
Fibonacci era un matematico del XII secolo che scoprì questa
sequenza di numeri, che comincia con due 1 e ogni numero
successivo è la somma dei due che lo precedono:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55… e via di seguito.
Fibonacci giunse a questa sequenza cercando una legge che
descrivesse la crescita di una popolazione di conigli, in seguito si
è scoperto che è una successione che ha profondi legami con la
natura osservando i numeri di petali e di foglie: esse sono quasi
sempre due, tre o cinque: ecco perché è più facile trovare un
trifoglio che un quadrifoglio. I numeri di Fibonacci sono
strettamente legati al rapporto aureo, un altro numero frequente
in natura.
Il rapporto aureo (φ) equivale a
, cioè a circa 1,618.
Questo rapporto si trova in un
rettangolo molto particolare ma
anche nei pentagoni e nelle stelle
a cinque punte, quindi nelle mele.
Se prendiamo come esempio la
stella che troviamo tagliando una
mela al suo equatore, scopriamo
che la distanza tra la prima e la
terza punta è pari a φ volte la distanza tra due punte adiacenti.
Il rapporto tra due numeri di Fibonacci consecutivi è molto
vicino a phi: 3/2= 1,5; 5/3=1,6; 89/55=1,618! Quindi i numeri di
Fibonacci e φ sono strettamente legati tra loro.
Tornando alle piante, si può notare che dagli steli germogliano
foglie singole, che spuntano con angolazioni diverse e disposte a
spirale. L‛angolo che separa una foglia è di 137-139 gradi. Qual è
il significato di questo angolo? Per scoprirlo bisogna risalire alla
fase iniziale di crescita della pianta: i germogli spuntano sullo
stelo uno alla volta e ciascuno si posiziona il più lontano possibile
dal precedente. Questo comportamento è dovuto alla necessità di
ogni germoglio di conquistare la maggior quantità possibile di
spazio e luce. Accade quindi che un angolo strettamente collegato
a φ sia particolarmente adatto a mantenere i germogli alla
massima distanza l‛uno dall‛altro: dividendo 365 gradi, per φ
otteniamo 222,5 gradi che, in senso orario, equivalgono a 137,5
gradi in senso antiorario, il numero così ricorrente tra le piante.
Nel caso del sesto germoglio accade qualcosa di diverso, come è
possibile vedere in questa figura. Visti dall‛alto, tutti i germogli
appaiono a circa 50 gradi di distanza, mentre il sesto è solo a
32,5 gradi dal primo, quindi è destinato ad avere meno spazio e
meno luce. Ecco perché la maggior parte delle piante ha solo
cinque foglie.
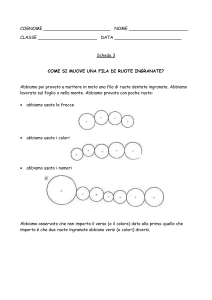
Le ruote e perché gli animali non le hanno
Il cerchio è molto importante in natura, esiste però un ambito in
cui è assente. Una delle più importanti applicazioni del cerchio è
costituita dalla ruota. Perché le ruote sono rotonde? Innanzitutto
lo sono perché una delle proprietà del cerchio è quella di avere un
diametro costante che permette di assicurare al
carico un‛andatura regolare. I cerchi, comunque,
non sono le uniche figure con diametro costante:
se prendiamo un triangolo equilatero e tracciamo
da ciascun vertice un arco che intersechi gli altri
due, otteniamo una figura con diametro
costante. Tuttavia non sarebbe efficace come ruota, in quanto le
ruote necessitano di assi: il cerchio infatti possiede una qualità in
più, cioè un centro equidistante da tutti i punti della
circonferenza. Quindi la ruota ha un asse centrale sempre nella
stessa posizione, mentre nell‛ipotetica ruota triangolare l‛asse si
sposterebbe continuamente su e giù. La ruota consente un
risparmio di energia, trasporto senza attrito: le ruote non
strisciano mai sul terreno perché di volta in volta la parte di
ruota che tocca il suolo è immobile. Ma se le ruote sono così
efficienti, perché gli animali ne sono sprovvisti? I canguri non
attraversano il deserto australiano su due ruote, ma saltellando
sui loro arti inferiori. La spiegazione chiama in causa la presenza
degli assi: se gli animali avessero ruote con assi e quindi anche
relativi legamenti e vasi sanguigni, dopo un paio di rotazioni si
creerebbe un orrendo groviglio. La capacità di rotolare sarebbe
tanto utile nel caso delle ruote quanto pericolosa nel caso delle
uova. Esse hanno solitamente una sezione circolare, un uovo
quadrato causerebbe problemi nel deporlo ma un uovo sferico
rotolerebbe lontano dalla madre con facilità. Facendo rotolare un
uovo di gallina, invece, torna indietro come un boomerang.
I legami tra natura e matematica
Una delle sfide più entusiasmanti di tutte le età è quella di trovare un quadrifoglio, ritenuto un
grande portafortuna: questa ricerca però, in realtà è sempre fonte di delusione. È ragionevole
pensare che da qualche parte vi sia un quadrifoglio, quindi perché la natura è così avara di
quadrifogli? Osservando i fiori si nota che la maggior parte di essi è composta da cinque petali,
numero che ritorna anche nella disposizione dei semi: è possibile osservarlo tagliando una mela al
suo “equatore”, notando che i semi sono sistemati all‛interno di una bella stella a cinque punte. Nel
mondo vegetale prevalgono quindi i numeri dispari, mentre in quello animale i pari (le zampe sono
sempre pari). Un‛indagine più accurata rivela che anche altri numeri sono piuttosto ricorrenti tra le
piante: esaminando un ananas o una pigna si nota che hanno file spiraliformi che si susseguono dalla
cima alla base, l‛una in senso opposto all‛altra. Di solito queste file in un ananas sono 8 e 13, mentre
in una pigna 13 e 21 o 21 e 34. Anche nei girasoli si possono individuare spire di semi che vanno dal
centro all‛esterno in senso orario e antiorario, il loro numero è solitamente di 34 e 55 o 55 e 89. I
numeri 8, 13, 21, 34 e 55 sono i più comuni: non è un caso, esiste un legame profondo tra natura e
matematica, natura e i numeri di Fibonacci.
Fibonacci era un matematico del XII secolo che scoprì questa sequenza di numeri, che comincia con
due 1 e ogni numero successivo è la somma dei due che lo precedono:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55… e via di seguito.
Fibonacci giunse a questa sequenza cercando una legge che descrivesse la crescita di una
popolazione di conigli, in seguito si è scoperto che è una successione che ha profondi legami con la
natura osservando i numeri di petali e di foglie: esse sono quasi sempre due, tre o cinque: ecco
perché è più facile trovare un trifoglio che un quadrifoglio. I numeri di Fibonacci sono
strettamente legati al rapporto aureo, un altro numero frequente in natura.
Il rapporto aureo (φ) equivale a
, cioè a circa 1,618. Questo rapporto si trova in un
rettangolo molto particolare ma anche nei pentagoni e nelle stelle a
cinque punte, quindi nelle mele. Se prendiamo come esempio la
stella che troviamo tagliando una mela al suo equatore, scopriamo
che la distanza tra la prima e la terza punta è pari a φ volte la
distanza tra due punte adiacenti. Il rapporto tra due numeri di
Fibonacci consecutivi è molto vicino a phi: 3/2= 1,5; 5/3=1,6;
89/55=1,618! Quindi i numeri di Fibonacci e φ sono strettamente
legati tra loro.
Tornando alle piante, si può notare che dagli steli germogliano foglie singole, che spuntano con
angolazioni diverse e disposte a spirale. L‛angolo che separa una foglia è di 137-139 gradi. Qual è il
significato di questo angolo? Per scoprirlo bisogna risalire alla fase iniziale di crescita della pianta:
i germogli spuntano sullo stelo uno alla volta e ciascuno si posiziona il più lontano possibile dal
precedente. Questo comportamento è dovuto alla necessità di ogni germoglio di conquistare la
maggior quantità possibile di spazio e luce. Accade quindi che un angolo strettamente collegato a φ
sia particolarmente adatto a mantenere i germogli alla massima distanza l‛uno dall‛altro: dividendo
365 gradi, per φ otteniamo 222,5 gradi che, in senso orario, equivalgono a 137,5 gradi in senso
antiorario, il numero così ricorrente tra le piante. Nel caso del sesto germoglio accade qualcosa di
diverso, come è possibile vedere in questa figura. Visti dall‛alto, tutti i germogli appaiono a circa 50
gradi di distanza, mentre il sesto è solo a 32,5 gradi dal primo, quindi è destinato ad avere meno
spazio e meno luce. Ecco perché la maggior parte delle piante ha solo cinque foglie.
Le ruote e perché gli animali non le hanno
Il cerchio è molto importante in natura, esiste però un ambito in cui è assente. Una delle più
importanti applicazioni del cerchio è costituita dalla ruota. Perché le ruote sono rotonde?
Innanzitutto lo sono perché una delle proprietà del cerchio è quella di avere un diametro costante
che permette di assicurare al carico un‛andatura regolare. I cerchi, comunque, non
sono le uniche figure con diametro costante: se prendiamo un triangolo equilatero e
tracciamo da ciascun vertice un arco che intersechi gli altri due, otteniamo una
figura con diametro costante. Tuttavia non sarebbe efficace come ruota, in
quanto le ruote necessitano di assi: il cerchio infatti possiede una qualità in più,
cioè un centro equidistante da tutti i punti della circonferenza. Quindi la ruota ha
un asse centrale sempre nella stessa posizione, mentre nell‛ipotetica ruota triangolare l‛asse si
sposterebbe continuamente su e giù. La ruota consente un risparmio di energia, trasporto senza
attrito: le ruote non strisciano mai sul terreno perché di volta in volta la parte di ruota che tocca il
suolo è immobile. Ma se le ruote sono così efficienti, perché gli animali ne sono sprovvisti? I
canguri non attraversano il deserto australiano su due ruote, ma saltellando sui loro arti inferiori.
La spiegazione chiama in causa la presenza degli assi: se gli animali avessero ruote con assi e quindi
anche relativi legamenti e vasi sanguigni, dopo un paio di rotazioni si creerebbe un orrendo
groviglio. La capacità di rotolare sarebbe tanto utile nel caso delle ruote quanto pericolosa nel caso
delle uova. Esse hanno solitamente una sezione circolare, un uovo quadrato causerebbe problemi nel
deporlo ma un uovo sferico rotolerebbe lontano dalla madre con facilità. Facendo rotolare un uovo
di gallina, invece, torna indietro come un boomerang.
Il problema dei ponti di Königsberg
Sulle coste del Mar Baltico, tra Lituania e Polonia, sorge
l'anonima città russa di
Kaliningrad, Königsberg ai
tempi della dominazione
prussiana; essa sorge sulle
rive del fiume Pregel e
presenta due estese isole
connesse tra di loro e con le
due aree principali della città
da sette ponti, come è
possibile vedere nell'immagine
a sinistra. Un passatempo
molto diffuso tra gli abitanti della città nel XVII secolo era cercare di
determinare un percorso che, passando per ogni ponte e una sola volta,
consentisse di tornare al punto di partenza. La soluzione la trovò Eulero, uno dei più grandi
matematici di tutti i tempi, contribuendo allo sviluppo di due branche della matematica: la topologia
e la teoria dei grafi. All'apparenza è una prova molto banale, ma in realtà è piuttosto complessa.
Quando Eulero venne a conoscenza del problema, nessuno aveva risolto il rompicapo, e decise di
dimostrare che il problema non ammetteva nessuna soluzione. Per analizzare il quesito convertì la
mappa dei ponti in un diagramma a rete.
Dal punto di vista matematico lo schema è equivalente alla mappa della città: i punti contrassegnati
dalle lettere indicano le due sponde del fiume (A e D) e le due isole (B e C); le linee indicano i ponti
che collegano questi quattro punti. Eulero classificò ciascun punto o nodo come «pari» o «dispari»,
pari in presenza di un numero pari di linee che hanno origine da quel punto, dispari se il numero di
linee è dispari. Dopo aver analizzato altre reti oltre a quella di Königsberg, Eulero dimostrò che è
possibile formare un circuito percorrendo una sola volta ciascun ponte, soltanto in presenza di due
nodi dispari oppure di soli nodi pari. In tutti gli altri casi è impossibile concludere il circuito senza
tornare sui propri passi. Eulero giunse anche a un'altra conclusione: in presenza di due nodi dispari,
il circuito deve necessariamente partire da uno di essi e concludersi sull'altro. Ecco dunque che
essendo i quattro nodi di Königsberg tutti dispari, non è possibile trovare un percorso che soddisfi
i requisiti posti inizialmente. Nel tardo XIX secolo venne costruito l'ottavo ponte e la città venne
dunque eulerizzata. Dove doveva essere costruito l'ottavo ponte? È semplice dimostrarlo grazie al
teorema di Eulero. Altri curiosi problemi da risolvere relativi alla città di Königsberg e i suoi ponti
si trovano qui.
La matematica e le coincidenze
Nella nostra vita accadono coincidenze eccezionali che ci impressionano e che vale la pena di
raccontare, ma dietro ad esse non c'è nulla di paranormale: possono spesso essere spiegate
matematicamente.
Un esempio è quello dei compleanni in comune. Spesso i bambini di una classe elementare rimangono
stupiti e impressionati se due di loro compiono gli anni lo stesso giorno; facendo un'analisi
matematica si può scoprire che dietro a questo fatto non c'è nulla di insolito: bastano infatti 23
alunni in una classe perché la probabilità che due di questi siano nati lo stesso giorno superi il 50%.
Per capire come questo possa accadere, è necessario premettere che, per calcolare la probabilità
che due eventi A e B avvengano contemporaneamente, bisogna moltiplicare la probabilità di A per
quella di B. Per esempio, lanciando in aria una moneta, la probabilità che esca due volte "testa" è
1/2 × 1/2 = 1/4, cioè 1 su 4. Come nel caso del lancio della moneta, anche il compleanno di un
bambino è indipendente da quello di un altro (gemelli esclusi, ovviamente). È quindi possibile
calcolare la probabilità di un compleanno in comune moltiplicando la probabilità relativa a ogni
bambino, come per la moneta. Invece di calcolare la probabilità di coincidenza di date è meglio, per
comodità, calcolare la probabilità che tutti i bambini siano nati in giorni diversi. Ipotizziamo che la
classe sia composta da due alunni e che il compleanno di uno di loro sia il 16 giugno. La probabilità
che il compleanno dell'altro bambino cada in un giorno diverso è di 364/365. Se si aggiunge un altro
alunno e i primi due compiono gli anni in giorni diversi, la probabilità che il terzo li compia in un
giorno differente dagli altri due scende a 363/365 e così via, per arrivare a 343/365 per il
ventitreesimo bambino. Quindi calcoliamo qual è la probabilità complessiva che ognuno dei 23
bambini presenti sia nato in un giorno diverso dagli altri: dobbiamo moltiplicare tutte le probabilità
relative a ciascun bambino, come abbiamo fatto per la moneta:
Da questo calcolo si ricava che la probabilità che nessuna coppia di bambini in una classe composta
da 23 alunni abbia il compleanno in comune è pari al 49%, circa la metà. Quindi il rimanente 51%
corrisponde alla probabilità che almeno due bambini abbiano il compleanno in comune. Quindi, se
prendiamo in considerazione una coppia precisa di due bambini, la possibilità che abbiano il
compleanno in comune è 1 su 365, mentre se consideriamo due bambini qualsiasi la probabilità
aumenta a 1 su 2.
Matematica e statue
Il problema di un turista che si ferma ad ammirare una statua di notevoli dimensioni è trovare la
distanza ottimale dalla quale osservare la statua. La colonna di Nelson a Trafalgar Square, a
Londra, costituisce un ottimo esempio. L'ammiraglio Nelson si trova in posizione rialzata; la statua
è alta 5 metri più i 49 del piedistallo. Se ci avviciniamo alla base della colonna e alziamo lo sguardo
riusciamo a vedere l'ammiraglio per intero, ma apparirà piuttosto schiacciato poichè l'angolo di
visuale è molto piccolo. Quindi conviene indietreggiare per riuscire a vedere sempre meglio la
statua grazie all'aumento dell'angolo di visuale. Esiste un punto ottimale in cui è possibile vedere la
statua con l'angolo più ampio possibile: il punto migliore è quello in cui i nostri occhi vengono a
trovarsi sulla retta tangente alla circonferenza passante per il cappello e i piedi di Nelson, come
illustrato nella figura. In questo caso la distanza ottimale è di circa 50 metri.
Sotto la pioggia è meglio correre o camminare?
Ognuno di noi che si sia trovato a camminare sotto la pioggia si è chiesto almeno una volta se
affrettare il passo gli avesse permesso di bagnarsi un po‛ di meno.
Quando ci muoviamo sotto la pioggia veniamo bagnati dalla pioggia che cade verticalmente (sulla
testa) e da una certa quantità di pioggia che ci investe orizzontalmente. Il ragionamento si può
generalizzare anche nel caso in cui piove “a vento”.
Le caratteristiche del soggetto che cammina sotto la pioggia sono state semplificate in quelle di un
parallelepido: ciò ci permette di separare al componente verticale e orizzontale della pioggia. La
componente verticale (PY) della pioggia è inversamente proporzionale alla velocità (v) con cui ci
muoviamo: meno si sta sotto la pioggia meno ci si bagna. La componente orizzontale (PX) della
pioggia è costante indipendentemente dalla velocità perché la maggiore quantità è bilanciata dal
minor tempo di esposizione quando corriamo. In formule:
PY (v) = Z / v (dove Z è una quantità media di riferimento)
PX (v) = C (costante)
P (v) = PY (v) + PX (v) = ( Z / v ) + C
L‛unico valore che modifica la quantità totale di pioggia, essendo Z e C costanti, è appunto la
velocità di spostamento.
Quindi la soluzione è: ci si bagna di più camminando. Se inizia a piovere e non avete l‛ombrello
mettetevi a correre!
Matematica e sfortuna
Nella vita di tutti i giorni accadono in continuazione fatti che ci fanno pensare di essere i soliti
sfortunati: pioggia durante le vacanze, tartine che cadono dal lato imburrato... la spiegazione della
sfortuna è sia matematica che psicologica. Si dice che "le disgrazie non arrivano mai sole", in realtà
questo detto dipende dalla durata e dalla gravità dell'episodio. Innanzitutto bisogna definire cos'è
una disgrazia: è un evento negativo, con una gravità variabile. Perdere il treno è meno grave
dell'allagamento della casa. Più a lungo un episodio negativo resta in mente, maggiore è la
probabilità di affrontare altre disgrazie: ad esempio, se si allaga la nostra casa e un mese dopo
subiamo un incidente in macchina tendiamo proprio a pensare di essere sfortunati; invece se
perdiamo il treno due volte nell'arco di un mese non ce ne rendiamo conto, eppure sono sempre due
eventi negativi in un mese. Nel caso dei due incidenti gravi non siamo riusciti a dimenticare il primo
e quindi la nostra mente collega i due fatti come fossero un'unica sequenza, c'è la tendenza a
cercare gli episodi che confermano la nostra fortuna e tutti gli altri positivi vengono ignorati: mai
nessuno dirà: «Mi è successa una sola disgrazia, il proverbio è falso».
Sfortuna e cartine
Spesso, consultando un atlante, scopriamo che il paese che dobbiamo raggiungere è proprio sul
bordo della pagina e siamo costretti a voltare pagina in continuazione per trovare la strada giusta
da percorrere. Eppure in una cartina i margini sono piccoli rispetto alla parte centrale del foglio.
Oppure no? In realtà la possibilità di scegliere una meta vicino al bordo è molto più elevata di
quanto si possa pensare:
Quindi i problemi sorgono quando la destinazione si trova nell'area ombreggiata, costituita da un
margine di un solo centimetro, irrilevante. Ma non è così: l'area dell'ombreggiatura è di 56 cm², il
28% della pagina. Abbiamo quasi una probabilità su tre che la destinazione sia nella zona
incriminata. Se poi consideriamo un margine di due centimetri, la probabilità che la destinazione sia
su quel bordo è ben del 47%! Come sempre, si tende a dimenticare il numero di volte in cui la
strada era perfettamente al centro della cartina, mentre ricordiamo quante volte non lo è stato,
ecco perché arriviamo a ritenerci sfortunati.
Il «13» sfortunato
Il 13 è da sempre considerato un numero sfortunato sebbene non sia ben chiara l'origine di questa
superstizione. Gli architetti superstiziosi evitano il 13° piano e gli scrittori superstiziosi saltano il
13° capitolo. Il numero è associato a episodi negativi, il più conosciuto è sicuramente l'Ultima Cena.
Venerdì 13 è il giorno peggiore in cui qualsiasi evento possa accadere e sfortuna vuole che è molto
più probabile che il tredicesimo giorno del mese sia di venerdì piuttosto che qualsiasi altro girono.
Si tratta di una «fortunata» combinazione statistica derivante dal ciclo dei giorni nel calendario
gregoriano.
La matematica nei cavolfiori
Sembra incredibile, ma il cavolfiore ha il suo grosso contenuto di matematica. È la forma a renderlo
nobile, il cavolfiore ha infatti una propria organizzazione e struttura interna. Mentre un fiore
dispone i suoi "enti minimi" (i petali) attorno a un corpo centrale, il cavolfiore è molto più
complesso: non ha né corpo centrale, né enti minimi. Staccando uno dei "rami" principali si vede che
il nuovo pezzo, più piccolo dell'ortaggio intero, è organizzato in maniera identica: molti rami che si
diramano a loro volta. La proprietà per cui un intero assomiglia a una parte di se stesso si chiama
autosimilarità, e caratterizza oggetti detti frattali. Con un cavolfiore dopo sei-sette passaggi
diventa impossibile continuare a separarlo in pezzetti simili, ma immaginando di avere un cavolo
perfetto e mani precisissime, si potrebbe proseguire all'infinito. Accade analogamente con alcuni
oggetti matematici costruiti sfruttando l'autosimilarità, come il fiocco di Koch. La costruzione del
fiocco parte di un triangolo equilatero. Ogni lato viene diviso in tre segmenti uguali; quello centrale
diventa la base di un altro triangolo equilatero, si ottiene una stella a sei punte e così via
all'infinito. Il fiocco ha un'area pari a circa 8/5 del triangolo iniziale, ma un perimetro infinito.
La famiglia di fogli A
Nei paesi europei le dimensioni dei fogli di carta sono standardizzate secondo la convenzione
ISO216. Le misure di un fogli A4, 21×29,7 cm, sembrano insensate, ma non è così. Infatti il foglio
A4 ha una caratteristica molto elegante: piegando a metà il lato maggiore si ottengono due fogli
che hanno le stesse proporzioni di quello di partenza. Quindi un volantino stampato su un foglio A5
può essere ingrandito fino a riempire un A4 senza subire deformazioni. Quindi il rapporto tra le
dimensioni di un A4 è uguale a quello di un A5, sempre 1,41. Questa proprietà vale sempre
raddoppiando o dimezzando i fogli considerati: vale quindi anche per l'A3 e l'A6. Maggiore è il
numero dopo la A, più piccolo è il foglio, e si può procedere all'infinito, minore è il numero, più
grande è, per arrivare all'A0 che misura 84,1×118,9 cm. E il rapporto tra le dimensioni è sempre di
1,41, ma la principale caratteristica dell'A0 è che la sua area è di un metro quadrato. Quindi l'A0
deve avere l'area di un metro quadrato e, se diviso a metà, deve generare fogli con lo stesso
rapporto tra i lati. Possiamo quindi impostare il seguente sistema in cui a e b sono le misure dei lati
del foglio:
Le soluzioni, cioè le misure di a e b , che soddisfano le condizioni sono:
0.
Fonti
Probabilità, numeri e code di Rob Eastway, Jeremy Wyndham – 2003 Ed. Dedalo,
Bari
Insalate di matematica di Robert Ghattas – 2004 Sironi Editore, Milano
http://www.wikipedia.org
http://www.chiesi.net/home/ita/giochi.html
http://www.html.it per la calcolatrice