Teoria dell’informazione e della trasmissione
Esercizio: informazione mutua e capacità di canale
Si consideri un canale con ingresso binario x = ±1 e rumore additivo indipendente (da x) discreto
n = ±1 , uniforme ( PN (n = −1) = PN (n = +1)= 1 2 ).
Calcolare la capacità di canale e spiegare in modo “intuitivo” il valore ottenuto.
Soluzione
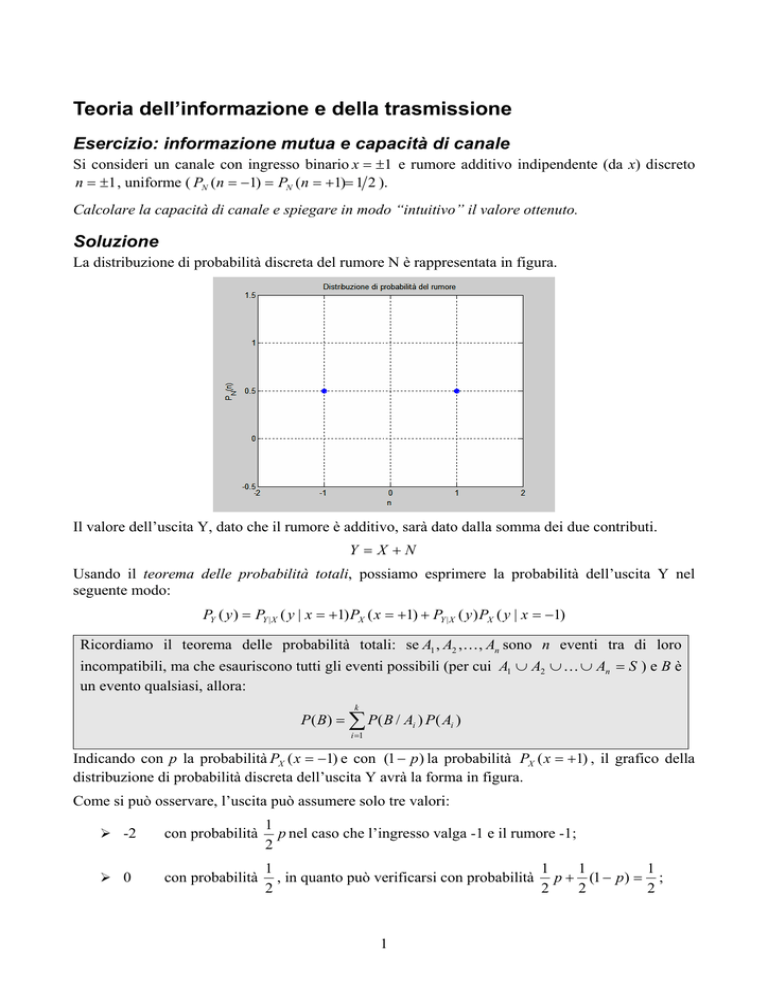
La distribuzione di probabilità discreta del rumore N è rappresentata in figura.
Il valore dell’uscita Y, dato che il rumore è additivo, sarà dato dalla somma dei due contributi.
Y =X +N
Usando il teorema delle probabilità totali, possiamo esprimere la probabilità dell’uscita Y nel
seguente modo:
PY ( y ) = PY | X ( y | x = +1) PX ( x = +1) + PY | X ( y ) PX ( y | x = −1)
Ricordiamo il teorema delle probabilità totali: se A1 , A2 , K, An sono n eventi tra di loro
incompatibili, ma che esauriscono tutti gli eventi possibili (per cui A1 ∪ A2 ∪ K ∪ An = S ) e B è
un evento qualsiasi, allora:
k
P ( B) = ∑ P( B / Ai ) P( Ai )
i =1
Indicando con p la probabilità PX ( x = −1) e con (1 − p) la probabilità PX ( x = +1) , il grafico della
distribuzione di probabilità discreta dell’uscita Y avrà la forma in figura.
Come si può osservare, l’uscita può assumere solo tre valori:
¾ -2
con probabilità
1
p nel caso che l’ingresso valga -1 e il rumore -1;
2
¾ 0
con probabilità
1
1
1
1
, in quanto può verificarsi con probabilità p + (1 − p) = ;
2
2
2
2
1
¾ +2
con probabilità
1
(1 − p) , nel caso che l’ingresso valga +1 e il rumore +1.
2
Il problema chiede di calcolare la capacità di canale (C): questa non è altro che la massima
informazione mutua, al variare della distribuzione di probabilità dell’ingresso X.
C = max I ( X , Y )
PX ( x )
L’informazione mutua può essere definita in due modi:
1. I ( X , Y ) = H ( X ) − H ( X | Y ) ;
2. I ( X , Y ) = H (Y ) − H (Y | X ).
Per l’esercizio, useremo la seconda definizione.
Ricordiamo la definizione di entropia e di entropia condizionata.
H (Y ) = ∑ PY ( y i ) log
Entropia:
i
Entropia condizionata:
1
PY ( y i )
H (Y | X ) = ∑ PX ( x j )∑ PY | X ( y i | x j ) log
j
i
1
PY | X ( y i | x j )
N.B.: I logaritmi sono in base 2.
Cominciamo a calcolare H (Y ) .
H (Y ) = PY ( y = −2) log
1
1
1
+ PY ( y = 0) log
+ PY ( y = +2) log
PY ( y = −2)
PY ( y = 0)
PY ( y = +2)
1
1
1 1
1
p log
+ + (1 − p ) log
1
1
2
2 2
(1 − p )
p
2
2
2
2
1
H (Y ) = p log + 1 + (1 − p ) log
2
1 − p
p
H (Y ) =
H (Y ) =
1
1
1
p log 2 + log + 1 + (1 − p ) log 2 + log
2
1 − p
p
2
H (Y ) =
1
1
1
p 1 + log + 1 + (1 − p )1 + log
p
1 − p
2
H (Y ) =
1
1
1
p + p log + 1 + (1 − p ) + (1 − p ) log
p
1 − p
2
H (Y ) =
1
1
1
p/ + p log + 2 − p/ + (1 − p ) log
p
1 − p
2
H (Y ) =
1
1
1
2 + p log + (1 − p ) log
p
1 − p
2
1
1
1
H (Y ) = 1 + p log + (1 − p ) log
p
1 − p
2
1
H (Y ) = 1 + H 2 [ p ]
2
Ora calcoliamo H (Y | X ) .
1
1
1
+
+ PY| X (0 | −1) log
+ PY| X (+2 | −1) log
H(Y | X ) = PX (−1) PY| X (−2 | −1) log
−
−
−
+
−
P
P
P
(
2
|
1
)
(
0
|
1
)
(
2
|
1
)
Y
|
X
Y
|
X
Y
|
X
1
1
1
+ PX (+1) PY| X (−2 | +1) log
+ PY| X (0 | +1) log
+ PY| X (+2 | +1) log
−
+
+
+
+
P
P
P
(
2
|
1
)
(
0
|
1
)
(
2
|
1
)
Y| X
Y| X
Y| X
1
1
1
1
1
1
1
1
H(Y | X ) = p log + log + 0 + (1− p) 0 + log + log
1
1 2
1
1 2
2
2
2
2
2
2
1
1
1
1
H(Y | X ) = p log2 + log2 + (1− p) log2 + log2
2
2
2
2
H(Y | X ) = p +1− p = 1
Il risultato ottenuto è molto interessante: H (Y | X ) non dipende dalla distribuzione di probabilità
dell’ingresso. Questo perché il rumore additivo è indipendente dall’ingresso.
L’espressione dell’informazione mutua, da massimizzare, è dunque:
I ( X ,Y ) = 1 +
1
1
H 2 [ p] − 1 = H 2 [ p]
2
2
In figura è rappresentato l’andamento di H 2 [ p ] in funzione di p. Come già sapevamo, H 2 [ p ] ha un
1
punto di massimo per p = che vale 1.
2
1
1
C = max I ( X , Y ) = 1 = bit uso di canale
2
2
PX ( x )
Abbiamo quindi scoperto che la massima informazione mutua, in questo caso, l’abbiamo quando i
due ingressi sono usati con la stessa probabilità.
La capacità di canale è quindi 1/2. La spiegazione intuitiva è che nel 50% dei casi saprò riconoscere
esattamente l’ingresso ( y = −2 e y = +2 ) e nel 50% no ( y = 0 ).
3
4