strumenti della matematica

STRUMENTI DELLA MATEMATICA
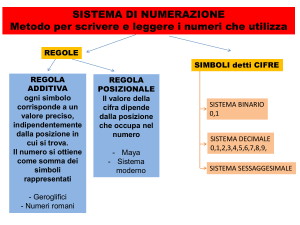
Tabelle a doppia entrata
Una tabella a doppia entrata è un riquadro con righe orizzontali e colonne verticali.
Il dato di una cella dipende dalla regola assegnata e dai dati in entrata della rispettiva
riga e colonna.
http://digilander.libero.it/enzomrd/images/propquadr.jpg
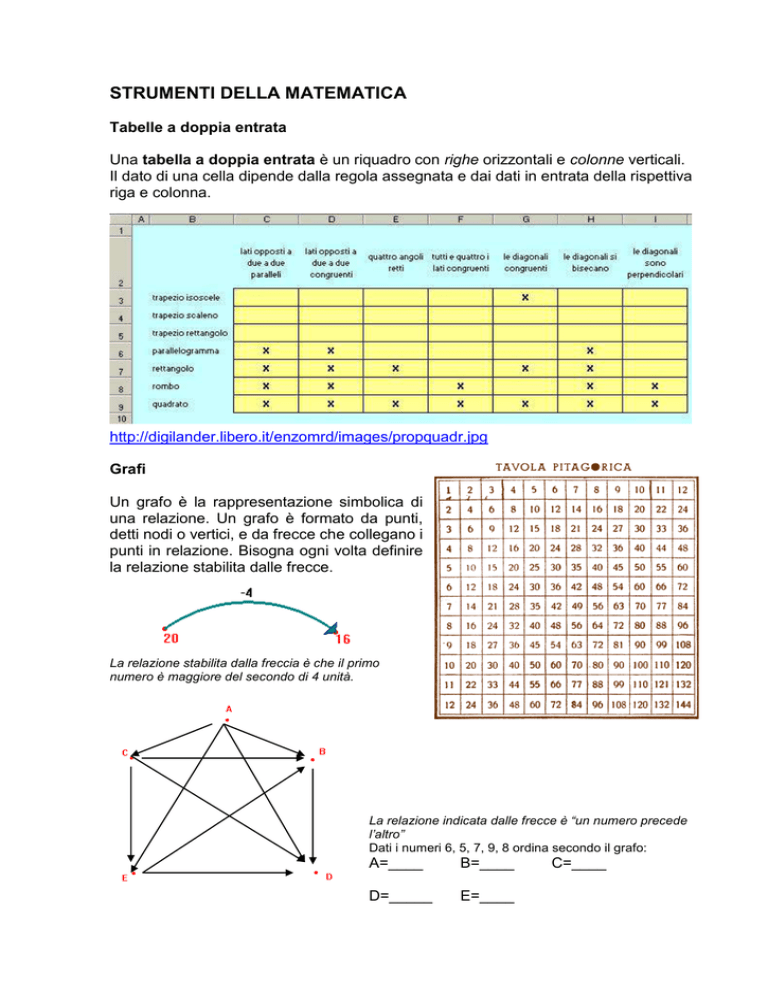
Grafi
Un grafo è la rappresentazione simbolica di
una relazione. Un grafo è formato da punti,
detti nodi o vertici, e da frecce che collegano i
punti in relazione. Bisogna ogni volta definire
la relazione stabilita dalle frecce.
La relazione stabilita dalla freccia è che il primo
numero è maggiore del secondo di 4 unità.
La relazione indicata dalle frecce è “un numero precede
l’altro”
Dati i numeri 6, 5, 7, 9, 8 ordina secondo il grafo:
A=____
B=____
D=_____
E=____
C=____
Lettere al posto dei numeri
La matematica usa come simboli i numeri, ma anche lettere.
Formule
L’uguaglianza A  b  h rappresenta la formula per determinare l’area di un
rettangolo.
A  bh
è vera per qualsiasi rettangolo (variando la base e l’altezza varia anche l’area):



b indica qualunque base del rettangolo
h indica qualunque altezza del rettangolo
b e h sono dette variabili
Equazione
L’uguaglianza A  6  9 si chiama equazione:
 La lettera A si chiama incognita;
 L’uguaglianza risulta vera per un solo valore di A, in questo caso A=54
L’equazione è una uguaglianza contenente almeno una variabile detta incognita che
risulta vera solo per determinati valori dell’incognita stessa.
2x=10 risulta vera solo x=5
5x – 2 = 13 risulta vera solo per x=3
Identità
E’ una uguaglianza contenente una o più variabili che risulta per qualsiasi valore
assegnato alle variabili.
a2-4= (a-2)(a+2) risulta vera per qualsiasi valore attribuito alla variabile
Funzione
E’ una uguaglianza contenente due variabili dette incognite in cui il valore di una
incognita dipende dal valore dell’altra.
xy=12 si legge “x per y uguale 12”
se x=3 allora y=4
se x=2 allora y=6
……..
x + y=10
se x=1 allora y=9
se x=3 allora y=7
……..
Sistema di numerazione decimale
I primi sistemi di numerazione furono di tipo additivo.
Il sistema posizionale decimale fu ideato, probabilmente, dagli indiani nel VI sec. d.C.
e trasmesso in Europa dagli arabi che, introdussero, l'uso della cifra zero.
Intorno al XIII sec. d.C. Leonardo Pisano (1170-1250),
detto Fibonacci. Introdusse in Italia il sistema
posizionale con i procedimenti per le operazioni.
L'introduzione del sistema decimale si può considerare
un’autentica rivoluzione confrontabile all'introduzione
del computer.
Evoluzione
dei
simboli
che
rappresentano le cifre dal 1000 al
1400
Sistema di numerazione decimale posizionale
 Decimale perché usa dieci simboli detti cifre e perché ogni 10 unità di un
ordine costituiscono una unità dell’ordine superiore.
 Posizionale perché la quantità di una cifra dipende dalla posizione che occupa
nel numero.
Cosa è il numero?
 Il numero è un insieme di simboli che indica una quantità
o I simboli che formano il numero sono dette cifre
o Ogni cifra ha due valori
 Un valore assoluto cioè la quantità caratteristica della cifra
 Un valore relativo cioè la quantità che dipende dalla sua
posizione nel numero
Quanti sono i numeri?
 I numeri sono infiniti
Quali sono i primi numeri utilizzati?
 I primi numeri utilizzati sono i numeri interi e per questo vengono detti numeri
naturali L’insieme dei numeri naturali è indicato con N
Le cifre 0, 2, 4, 6, 8 sono dette pari
Le cifre 1, 3, 5, 7, 9 sono dette dispari
Un numero è detto pari se la sua ultima cifra è pari
Un numero è detto dispari se la sua ultima cifra è dispari
Rappresentazione dei numeri naturali
1. Rappresentazione grafica mediante una semiretta suddivisa in una serie di
segmenti uguali
L’insieme dei numeri naturali è un insieme ordinato e infinito.
Esercizi
Risolvere le seguenti equazioni:
x + 2=10
x – 5=14
12 – x=7
5x=15
12 : x=4
x : 6=12
2x-6=x + 3
x=10 – 2
x=14 + 5=19
x=12 – 7=5
x=15 : 5=3
x=12 : 4=3
x= 6  12  72
2x – x=3 + 6
soluzione
x=9
Problemi con le equazioni:

Trova un numero sapendo che la sua metà, aumentata di 1, dà come risultato 7.
Semplificando si ha: “la sua metà aumentata di 1 dà 7 “ quindi (x : 2) + 1 = 7
(x : 2) + 1 = 7

Trova il numero che addizionato al suo doppio dà 54.
x + 2x =54

soluzione x : 2=7 – 1=6 cioè x= 2  6  12
soluzione
3x=54 cioè x=54:3=18
La somma di tre numeri pari consecutivi è 60. Trova i tre numeri.
x + (x+2) + (x+4) = 60
soluzione
x + x + 2 + x + 4 = 60
cioè 3x = 60 – 2 – 4=54
cioè x=54 : 3=18