sistemi di numerazione - Liceo Scientifico Nino Cortese Maddaloni

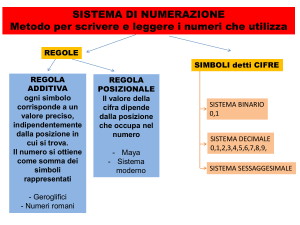
Un sistema di numerazione è l’insieme di regole e di simboli che
permettono la rappresentazione grafica dei numeri e la loro lettura.
I sistemi di numerazione del passato si basavano sul sistema
additivo, nel quale ad ogni simbolo era associato un valore
ben definito.
Gli antichi Egizi utilizzavano un sistema in cui un numero
era scritto accostando più simboli :
│
∩
1 10
9
100 1000
I Romani e i Greci usarono una numerazione simile a quella egizia,
con la possibilità di sottrarre due simboli se il maggiore era scritto a
destra del minore. Ad esempio: il numero romano XI corrisponde
al nostro 10+1=11, mentre il numero romano IX corrisponde al
nostro 10-1=9.
Per contare venivano usati gli abachi,
inizialmente tavolette di argilla sulle quali si
tracciavano solchi paralleli. nel solco più a destra
venivano allineati dei sassolini e quando il solco
era pieno, per esempio con 10 sassolini, si
toglievano tutti i sassolini e se ne metteva uno
solo nel solco posto alla sua sinistra e così via.
Gli abachi furono la prima calcolatrice dell’uomo
e per renderli più maneggevoli furono costruiti
con supporti in legno, su cui venivano fissati
alcuni bastoncini, lungo i quali scorrevano dei
dischetti forati che avevano lo stesso significato
dei sassolini. Senza l’abaco però non era possibile
distinguere numeri, quali 302, 320 o 32.
Si deve agli Indù l’assegnazione di un simbolo che indicava il vuoto e che
nelle altre traduzioni si trasformò in zero. Essi rappresentarono il vuoto con
un puntino, che nel tempo assunse la forma dell’attuale zero e divenne
una cifra. L’introduzione dello zero rese possibile l’abbandono dell’abaco.
Il sistema posizionale venne introdotto in Occidente nel Medioevo da
mercanti italiani che commerciavano con gli Arabi, i quali avevano
assimilato la cultura dai popoli indiani.
Fu grazie al matematico Fibonacci che (1170 – 1250) che il sistema di
numerazione posizionale fu divulgato in Occidente.
IL SISTEMA POSIZIONALE DECIMALE
Esso permette di rappresentare numeri, anche molto grandi, servendosi di pochi
simboli, il cui valore varia a seconda della posizione che occupano all’interno del
numero stesso.
I simboli utilizzati prendono il nome di cifre. Il loro numero costituisce la base del
sistema di numerazione.
Per esempio il sistema di numerazione che usiamo è detto decimale o in base
dieci, perché utilizza 10 cifre: 0 1 2 3 4 5 6 7 8 9 .
Probabilmente il motivo per cui si utilizza un sistema in base dieci sta proprio nel
fatto che il nostro supporto fisico di calcolo, la mano, ha appunto 10 dita.
Le prime 10 cifre costituiscono le unità del primo ordine del nostro sistema
decimale.
Al successivo di 9 vengono associate due cifre : 10, dove 0 rappresenta le unità e
1 la decina, o unità del secondo ordine.
Dieci decine formano un centinaio o unità del terzo ordine e così si possono
ottenere numeri sempre più grandi.
Perché è detto posizionale il nostro sistema decimale?
Se ad esempio considero il numero 222, la prima cifra a sinistra
indica 2 centinaia 2 𝑥 102 , la seconda indica 2 decine 2 𝑥 101 e
la terza 2 unità. La stessa cifra 2 assume valore diverso a seconda
della posizione che occupa il numero.
Per cui il numero 135 si potrà scrivere anche nella seguente forma
polinomiale :
𝟏𝟑𝟓 = 1𝑥102 + 3𝑥101 + 5𝑥100
= 1𝑥100 + 3𝑥10 + 5
SISTEMA BINARIO
Ai nostri giorni, nell’ambiente informatico, si ricorre alla numerazione in
base 2, che caratterizzata da due soli simboli : 0 e 1 associati a due stati
possibili dei componenti elettronici dei calcolatori.
Allo stato aperto si associa la cifra 0, allo stato chiuso si associa la cifra 1.
Per rappresentare un numero si utilizza, allora, un sistema posizionale in
base due, detto anche sistema binario.
Dalla traduzione inglese di « cifra binaria », binary digit, ognuna di
queste caselle è detta bit. Le otto caselle contengono 8 bit e
costituiscono una cella di memoria detta byte.
0
1
0
1
1
0
1
1
In informatica per indicare le dimensioni di un file si
utilizzano i multipli dei byte.
Un kilobyte 1 KB = 210 𝑏𝑦𝑡𝑒 = 1.024 𝑏𝑦𝑡𝑒
Un megabyte 1 MB = 1000 KB
Un gigabyte 1 GB = 1000 MB
PASSAGGIO DAL SISTEMA BINARIO AL DECIMALE
E VICEVERSA
Ma a che numero corrisponde nel nostro sistema decimale ?
𝟎𝟏𝟎𝟏𝟏𝟎𝟏𝟏𝟐 = 0𝑥27 + 1𝑥26 + 0𝑥25 + 1𝑥24 + 1𝑥23 + 0𝑥22 + 1𝑥21 + 1𝑥20
= 0 + 64 + 0 + 16 + 8
= 𝟗𝟏𝟏𝟎
+
0
+
2
+ 1
Ora osserviamo come si scrivono i primi numeri naturali nel sistema binario.
0 = 𝟎𝟐
1 = 𝟏𝟐
2 = 𝟏𝟎𝟐
3 = 𝟏𝟏𝟐
4 = 𝟏𝟎𝟎𝟐
5 = 𝟏𝟎𝟏𝟐
6 = 𝟏𝟏𝟎𝟐
7 = 𝟏𝟏𝟏𝟕
8 = 𝟏𝟎𝟎𝟎𝟐
9 = 𝟏𝟎𝟎𝟏𝟐
10 = 𝟏𝟎𝟏𝟎𝟐
e così via.
 Quali
caratteristiche ha un numero che termina con 0,
nel sistema binario ?
 Quali
caratteristiche ha invece un numero che
termina con 1 nel sistema binario ?
 Provate
ora voi a trasformare i numeri seguenti dal
sistema binario a decimale :
𝟏𝟏𝟎𝟎𝟏𝟎𝟐 𝒆 𝟏𝟎𝟎𝟏𝟏𝟐
𝟏𝟎𝟎𝟎𝟏𝟏𝟎𝟐 𝒆 𝟏𝟏𝟏𝟎𝟏𝟎𝟏𝟐
Ma come si trasforma un numero del sistema decimale a quello
binario?
Ad esempio 3410 = 1000102 , ma come è possibile ricavarlo?
Basta eseguire una semplice divisione per 2 !
34 2
0 17 2
1 8
2
Il risultato si ottiene considerando
0
4
2
0
2
2
0
1
2
1
0
tutti i resti dal basso verso l’alto.
 Adesso
provate voi a trasformare i seguenti numeri dal
sistema decimale al binario:
12510 𝑒 24010
36710
𝑒
58610