78
MECCANICA APPLICATA ALLE MACCHINE
Figura 4.2
Esempi di sistemi
di movimento
complessi:
a) riduttore
a più stadi,
b) robot
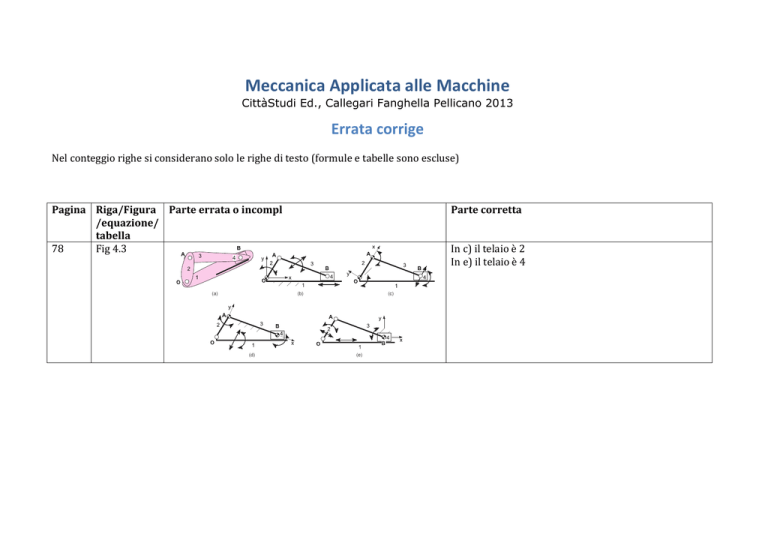
Meccanica Applicata alle Macchine CittàStudi Ed., Callegari Fanghella Pellicano 2013 Errata corrige Nel conteggio righe si considerano solo le righe di testo (formule e tabelle sono escluse) Figura 4.3
Esempi
di inversione
Pagina Riga/Figura Parte errata o incompl Parte corretta cinematica: catena
cinematica
con
3
(a)
(b)
/equazione/ coppie rotoidali
e una prismatica.
tabella 78 Fig 4.3 In c) il telaio è 2 In e) il telaio è 4 (b)
(a)
(d)
(c)
(e)
In Figura 4.3 sono mostrate varie inversioni cinematiche di una catena formata
da 4 corpi chiusi in una maglia da 3 coppie rotoidali (fra i corpi 1 e 2, 2 e 3, 3 e 4) e
una prismatica (fra il corpo 1 e il corpo 4). Nella Figura 4.3b, è assunto come telaio il
corpo 1 e da questo discendono alcune caratteristiche del movimento assoluto degli
altri corpi: il corpo 4, essendo vincolato al telaio da una coppia prismatica, potrà
solo traslare lungo una direzione fissa (orizzontale in figura) rispetto al riferimento
assoluto, il corpo 2, vincolato a telaio da una coppia rotoidale (punto O), potrà solo
ruotare attorno a questo punto, fisso, e, infine il corpo 3 vincolato ai corpi 2 e 4 tramite rotoidali, avrà un movimento piano di tipo generale (traslazioni in direzioni x e
y e rotazione). Questa configurazione è molto nota, essendo usata, ad esempio, nei
motori a combustione interna e in molte altre macchine, e sarà studiata in dettaglio
Capitolo 4_meccanica.indd 78
13/03/13 16:41
o) e modulo variabile. La geometria del meccanismo di sospensione posteriore
nibile in maniera del tutto analoga (Figura 4.7b), tenendo conto che i corpi 3 e
coppia prismatica che li connette (ammortizzatore) sono rappresentati da un
vettore a modulo e fase variabili (zBC).
81 dei meccanismi:
a) alzacristalli
automobilistico;
b) sospensione
posteriore
di bicicletta.
Fig. 4.7 Sul membro 4 il vettore è zBC 101
CINEMATICA DEI MECCANISMI PIANI
(a)
82 In Figura 4.24 vengono mostrati il quadrilatero e i suoi C.i.r. in una diversa posizione; in questo caso, la posizione di P24 interna (b)
al segmento P12P14 denota un rapporto w4/w2 di segno negativo. Data la posizione (interna a P12P13) di P23 il rapporto
w3righe /w2 è negativo
in questa
posizione.
8-­‐11 ancheNon è definito espicitamente il concetto di maglie Datibtre
corpi i, j eindipendenti k, e i loro rispettivi C.i.r. (Pij, Pjk e Pki), per il teorema di
dal asso Aronhold-Kennedy sempre allineati, vale la relazione, che definisce, in generale, il
rapporto di trasmissione fra due qualunque di essi:
81
13/03/13 16:41
tij = wj / wi = ± lPij_Pik / lPij_Pjk
(4.49)
con le condizioni sul segno prima discusse (segno positivo se Pij esterno al segmento
PjkPki).
Ad esempio, nel caso dei tre corpi di Figura 4.25, il portatreno 1, le due ruote 2
e 3, vincolate al portatreno da coppie rotoidali in P12 e P13 e fra di esse a un moto di
puro rotolamento nel punto di contatto P23 delle due circonferenze (r2 + r3 = l1), si ha:
1) i = 2, j = 3, k = 1 (rapporto di trasmissione fra le due ruote, considerato fermo il
portatreno):
t23 = w3 / w2 = – lP23_P12 / lP23_P13 = – r2 / r3
(4.50)
che costituisce il caso ben noto del rapporto di trasmissione fra due ruote; essendo
P23 interno agli altri 2 C.i.r, tale rapporto è negativo;
2) i = 2, j = 1, k = 3 (rapporto di trasmissione fra il portatreno 1 la ruota 2, considerata
ferma la ruota 3):
101 eq. 4.51 t21 = w1 / w2 = – lP21_P23 / lP12_P13 = r2 / l1
che è positivo, essendo P12 esterno agli altri 2 C.i.r.
(4.51)
Definizione di maglia indipendente: In un meccanismo, una maglia è un percorso chiuso formato da un'alternanza di corpi e coppie cinematiche. Un insieme di maglie che contiene tutti i corpi e le coppie del meccanismo, e che non può essere ridotto senza escludere almeno un corpo o una coppia è detto insieme di maglie indipendenti. La seguente formula di Eulero consente di determinare il numero di maglie indipendenti in un grafo: Numero_maglie_indipendenti=e-­‐v+1 in cui e= numero dei lati (edges) del grafo; v= numero dei vertici del grafo Per applicare questa formula a un meccanismo, basta considerare che i vertici del grafo corrispondono ai corpi del meccanismo, mentre le coppie (considerate con la loro molteplicità) ai suoi lati. τ 21 = ω 1 / ω 2 = lP 21_P 23 / lP12 _P13 = r2 / l1 Figura 4.25
Centri di istantanea
rotazione ruoteportatreno.
sono presenti
Figura 6.6
⎡ a ⎤bielle scariche, è opportuno identificarle per tenere conto della direzio2
xB forze scambiate: in questo modo il sistema di equazioni
(nota)⎢delle
che
dovrà
essere
Modellonormale
! 3 ×generale,
⎥ = a A + a rtB _ A + a rnB _ A =Nel
a A +caso
w
B
−
A
−
w
B
−
A
(4.63)
(
) l’accelerazione
) di A è composta dalla componente
3 (
semplificato
olto sarà
da 1 incognita (ed ovviamente 1 equazione) in meno, per cui
⎢⎣ caratterizzato
0 ⎥⎦
(accelerazione centripeta) dovuta al moto circolare di A, parallela a z2, e dalla comdella dinamica
ulta più semplice.
ponente tangenziale, ortogonale a z2, presente solo se l’accelerazione angolare della
verticale
incognite
axB e di3,azione
come ealreazione:
solito risolubili
percoppia,
il vettore
aB e
plicare
il principio
quando èsigraficamente
disconnette
una
nascono
manovella
non
nulla. Come
per le posizioni
e velocità, l’accelerazione
B dovrà
di undi
autoveicolo.
on
la
semplice
formula
=
a
/z
per
il
modulo
dell’accelerazione
angolare
2 membri che erano
2 forze
e contrarie,
cioè
con conto
lo stesso
modulo,
3terza rtB_A
3 uguali
103 in contatto
ressere
iga dal raggio tenendo
1
determinata
della
presenza di ambedue i corpi 3 e 4, e delle
1 o antiorario).
stessa
direzione e verso opposto (ovviamente
tali forze sono applicate l’una ad un
basso accelerazioni relative sia tangenziali sia normali (centripete) su ognuno di essi:
embro e l’altra al secondo membro): sempre per ridurre la complessità del successivo
106 eq 24nomi
.61 diversi a taliaforze=dia contatto,
oblema algebrico,
anziché dare
R=ed
+ artB_A +adaes.
a R+ , e (BFigura
– A) –4.29
w32 (B – A)
B_3
A
rtB_A ij A ji 3
Analisi
(4.61)
i imporre la relazione Rij = – Rji, è bene fin dall’inizio dare lo stesso nome alle 2 forze e
accelerazione
aB_4 = aC + artB_C + arNB_C = 4 (B –diC)
– w42 (B – C)
107 con i versi
fig 4opposti.
.29 egnarle nello schema
del biellarivere le equazioni
di equilibrio
di ciascuna
parte
sialostata
isolata e comporre
un sisteSi scelgano
come
coordinate
libere
spostamento
verticale
e, l’angolo
di di queste quattro
Essendo
per la
coppia rotoidale
B,zadel=baricentro
a = amanovella.
le incognite
B
B_4
B_3
a algebrico lineare
nei moduli
forze incognite.
beccheggio
q: delle
ipotizzando
piccole
oscillazioni,
di attacco
A e B si può essere risolto
equazioni
scalari
sono lei punti
quattro
variabilidelle
in aBsospensioni
, 3 e 4. Il problema
muovono
verticale
con
spostamenti
rispettivamente
di
z
=
z
+
aq
e
z
=
z
–
bq.
rificare che il sistema
sia sulla
ben posto
(ovvero
di
avere
tante
equazioni
quante
incognite)
A
B
graficamente tramite un poligono di vettori,
che rispetto
alL’enercaso delle velocità, è leggia cineticalee reazioni
quella potenziale
dell’auto
valgono
rispettivamente:
isolverlo per determinare
vincolari
e
le
altre
forze
esterne
eventualmente
germente più complesso a causa della presenza di nuovi vettori noti (le accelerazioni
ognite.
centripete, arNB_A =1– w322(B1– A)2e arNB_C = – w42(B – C), Figura 4.2�). Determinate dal
T (t ) = mz +tangenziali
J q
(6.30)
di accelerazione relativa,
artB_A = 3 (B – A), e
124 fig 5.9 poligono le componenti
2
2 G
raggio l1 a B_ 3 = a A + a rtB_A + a rnB_A = a A + ω! 3 × ( B − A ) − ω 32 ( B − A ) la freccia di artB_A va invertita Le parentesi sono sbagliate voglia ora effettuare l’analisi di accelerazione del meccanismo a ritorno rapido
esempio T23 (=-­‐T32) gura 4.19,, per il quale si assume, ad esempio, rotazione della2 manovella 2 a2 ve1
1
U(si
t ) ricava,
= mgz +direttamente,
ka ( z + aq ) +perkla
z − bq ) in
(6.31)
à costante, nota (qü2 = 2 = 0); da questo
(rotoidale
2 bessere svolta M E C C A N I C A A P P L I C A T A A L L E M A C C H I N E
i corpi 2 e 3, aB_2 = aB_3 = 170
– w22(B – O), che come in2 precedenza può
camente (Figura
4.30).P(t)
L’accelerazione
del puntosull’assale
B sul corpo
4 è determinata
La forza
che agisce direttamente
anteriore
va “proiettata” nelle direzioni
Capitolo 4_meccanica.indd
106
13/03/13 16:42
iderando,
come
per
le
velocità,
sia
il
moto
assoluto
del
corpo
il moto conoscere un solo valore del rendimento
delle coordinate libere, fornendo:
Si osserva che4è che
sufficiente
per stu vo fra i corpi 3 e 4, legato alla presenza di una diare
coppiail prismatica
fra
di
essi.
In
flusso di potenza diretto e retrogrado quando il rendimento è abbastan∂z
∂z
161 le due
eq. 6.32 vettoriali za
to modo si ottengono
relazioni
sottostanti:
coefficiente di attrito f, ovviamente
Qz (alto:
t ) = P sia
⋅ Ah(=fP) il rendimento funzione del(6.32)
Qz (t) = P ⋅ A = −P ∂
z
se f è piccolo
allora si può sviluppare in serie di McLaurin ottenendo ∂z
aB_4 = artB_A + arnB_A = 4 (B – A)h(0)
– w42=(B1:– A)
(4.64)
170 riga 5 non c’è apice su η r
∂h
aB_4 = aB_3 + arB4_3 + aBco4_3 = aB_3 + aB3_B4
h '(–f2w
) =3 h(0v)B4_B3
+
f +… 1 – e f con 0 < e << 1, da questa espressione si calcoli
∂f f =0
quali le incognite
sono
a
,
e
a
,
mentre
sono
note,
oltre a aB_3, tut1
1
B_4 6.16 4
172 fig. B4_B3
h
'( f ) =
= 1 – e f +… ; questo diil
rendimento
nel
flusso
retrogrado
accelerazioni dipendenti dalle velocità che sono la componente centripeta
1
h
(–
f
)
+
e
f
= Capitolo
– w42(B
– A) e l’accelerazione
di Coriolis aBco4_3 = – 2w3 vrB4_B3 che nasce a
6_meccanica.indd
161
13/03/13 16:44
mostra che se il rendimento è elevato si può assumere h h'.
a della presenza della velocità angolare del corpo 3 e della velocità relativa
i
6.4.3
mpio 5.1
F LU S S O D I P OT E N ZA N E L L E T R A S M I S S I O N I
onsideri il meccanismo schiaccia-lattine rappresentato in Figura 5.7b in cui
r= l
è già stato
notato,
nelle trasmissioni meccaniche il flusso di potenza si può a
; nell’ipotesi di poter trascurare gli attriti,Come
determinare
la forza
di compres2
13/03/13 16:42
volte invertire, per cui essa occasionalmente fluisce dall’utilizzatore
al motore: per
esercitata dal pistone in funzione della forza di comando
F
quando
q
=
30°.
studiare la dinamica della macchina, pertanto, occorre preventivamente accertarsi
Ni
dd 107
del verso del flusso di potenza e di conseguenza utilizzare il valore di rendimento
a di sviluppare l’analisi statica del meccanismo occorre
determinare
degli
appropriato
(direttoil hvalore
o retrogrado
hr).
d
i mostrati in Figura
5.10;
dal
teorema
dei
seni
si
ricava:
Laωdeterminazione
del flusso di potenza può essere a volte immediata, ad esempio
P =
P P = ηseP
173 eq. 6.68 (b) t1
r t2
t1
r t2
la macchina è a regime, ma in condizioni di moto vario le variazioni di energia cinetica
delle masse a monte e a valle della trasmissione possono portare a versi imprevisti di
2 = l → y = arcsen 2sen(
30flusso
°) = 45
° cui in questo caso
(5.2)è necessaria una analisi accurata. A tal fine, è possibile
tale
per
6.14
senq senFigura
y
Flusso di potenza
separare la macchina in 3 sottosistemi, come mostrato in Figura 6.14, e poi applicare
attraverso
a sistema:
ciascunoviene
di essi
l’equazione
di bilancio energetico. Si noti che in questo schema la
esto punto si traccia il diagramma di corpo libero del
indicata
con Rij la
le trasmissioni:
divide
in due
one vincolare che agisce sul corpo j per effetto deltrasmissione,
contatto con ilche
corpo
i; inoltre
taliil sistema, è supposta priva di inerzie per cui queste, se
l
(
)
relazione
una
legge lineare dello spostamento in funzione
eri ora uno spostamento xquesta
della massa
m verso il fornisce
basso, a tale
spostamenFigura 7.20 della forza
Figura 7.15, per effetto della deformazione strutturale il punto C si sposta verticalmenonde una variazione di lunghezza
dell’asta
BC e con
del molti
cavo gradi
AC. Sidiconsideri
la contropartita si perde in parte la fisica
Sistema
sistemi
complessi
libertà,
come
te
nel punto
C' (si ericordi
che il modello
è semplificato
e gli spostamenti
soF =orizzontali
AE
dimoto
coordinate
5, per effetto della deformazione
strutturale
ilnoti
punto
C la
si
sposta
verticalmenk
=
applicata;
si
ottiene
rigidezza
equivalente
.
Durante
il
vibratorio la
del
problema,
si
infatti
che
si
perdono
completamente
le
forze
elastiche,
il
cui
effetto
è
no trascurati, inoltre si trascura la variazione di b), ciò porta a determinare
per esempio
eq
lagrangiane
to C' (si ricordi che il modelloperò
è semplificato
e gli spostamenti
d2 2 L
incluso nell’energia
potenzialeorizzontali
elastica. sox 2x 1 senb ,
alternative.
la lunghezza
cavoa determinare
dopo l’applicazione
del carico: AC
ati, inoltre si trascura la variazione
dinotato
b), ciòdel
porta
per
esempio
1
Si è già
che
nellaalla
formulazione
il sistema
di–equazioni
presenta
unaelastica
matrice F = – k x, dall’equimassa
èrelazione
soggetta
forza
diattuale
inerzia
Fi =spostamenti
mẍ 1e alla
forza
el
eq
questa
può
essere
linearizzata
per
piccoli
x
e
può
essere
ge2
2
di massa
diagonale
le equazioni sono dunque accoppiate
ACe una1 di rigidezza
xC Anon-diagonale,
2x
zza
del cavo dopo
del
Fi + Fel = 0 211 l’applicazione
riga 1dinamico
6 carico:
M1=
E C0
Nottiene
I C1 senb
A A P, Pl’equazione
L I Cdel
A T cavo
A A LeL dell’asta
Edel
M Amoto:
C Cdopo
H I N la
E de226
librio
F
=
+
F
si
neralizzata
per
ottenere
le
lunghezze
approssimate
tramite
quest’ultima.
facileelxmostrare
che la geforma delle equazioni del moto non è unica
i Èpotenziale
azione può essere
linearizzata
per
piccoli
spostamenti
e può
essere
energie
cinetica
sono
date da:
V I B R A Z I O Nformazione,
I Le
Muno
E C stesso
CAN
I sistema
C H E e uno
227
mediante
sviluppo
in
serie
di Mcdalle
Laurin
in x arrestato
al primo ordine:
per
meccanico,
essa
dipende
coordinate
lagrangiane.
a per ottenere le lunghezze approssimate del cavo e dell’asta dopo la de! ℓ1 − xsenβ 215 riga 1
1 ʹ
ʹ
2e
è rappresentato
un
sistema
did’estremità
anziché
spostamento
operaʹ =7.7r
AInCFigura
ℓ 1Mc
+ Dℓ
" ℓ (1⎛− x senb
BC ʹ =⎛ordine:
ℓ coordinate
" ℓ 2 (⎞
1 − x sena
=7.20
ℓBarra
= ℓ +2 Dℓ ⎛alternativo,
longitudinale
con
massa
). Questa
e, mediante uno sviluppoEsempio
in serie
di
1Laurin
1 in x1 arrestato
⎞) primo
y! 1 + y! 2al
y! 22 – y! 12 ⎞ !! 2 AE
1
1
1
1
2
2
(7.4)
m
x, + ⎜U =convinti
=che
verticale
del
baricentro
gli
A (7.22)
e B;
di linearizzazione
quando
di ordine
⎟⎟ spostamenti
= è
melecita
JGè ⎜⎜ragionevolmente
+0 ki termini
ydei punti
Esempio 7.9rzione
Sistema
barra
diTtorsione
⎟kx1 yverticali
⎜ rotazione,
⎟⎟ +sisiscelgono
1
2 2
!
ℓ
−
xsen
α
riga 1ℓʹ21 .barra
Questa
opera− x senb )Sie consideri
BCleʹ =nuove
+ Dℓ 2 "diℓFigura
1 −⎜⎝legate
x7.10,
sena
ℓ 1 + Dℓ 1 " ℓ 1 (1215 =l’esempio
ℓcoordinate
(
)
la
ha
una
lunghezza
L
=
1
m
e
porta
una
massa
2
2
2
2
2
ℓ
+
ℓ
2
2
2
L
⎠
⎝
⎠
sono
alle
precedenti:
y
(t)
=
x
–
q
e
y
(t)
=
x
+
q;
da
cui
si
ha
⎝
⎠
1 ciò2è
superiore siano trascurabili; nel caso
x2<< 1,2. 2
specifico
1 vero quando
1
Un disco
rigido
montato
di una
barra
a sezione
circolare
piena
incastrata
earizzazione è lecita
quando
siL’energia
èèragionevolmente
convinti
inelle
termini
d’estremità
m potenziale
= 1all’estremo
kg, la barra
d’acciaio
–diy1ordine
ymolle
y1 è+costituita
yche
accumulata
è: e la sezione trasversale è tubo quadro
219 ruga 1
1 valida solo per ℓ1 = ℓ 2 2
2
nell’altra
estremità,
Figura
7.28.
Lexdimensioni
sono:
e . q = L = 2 m, D
. B = 4 cm, s = 1 cm, R = 20 cm.
siano trascurabili;
nel caso
ciòeèspessore
veroi termini
quando
x << 1,2
dispecifico
latoimmediatamente:
30
mm
1= mm.
si
sviluppino
necessari
per
le
equazioni
di
Lagrange:
+
2
notiè:lache
l’equazione
7.4 èeformalmente
identica alla 7.2, il sistema si comporta quindi
1
2
Calcolare
laSi
frequenza
propria
nelpropria.
caso di alluminio
acciaio.
potenziale accumulata
nelle
molle
Calcolare
frequenza
1
1 1
1
2
2
2
2
U
=
k
D
ℓ
+
k
D
ℓ
"
k
sen
b
+
k
sen
a x 2 = ⎤ keq x 2
(7.11)
219 EQ 7.23 1
1
⎡2 2 2 1 ⎤
⎡2
⎤
⎡
2
2
2
⎛
⎞
⎛ ∂T ⎞ ⎡ m
JG
JG
J
J
AE
d 7.20
Figura
m
m
d
∂T
Svolgimento
1
1
1
1
⎢
⎥
⎢
⎥
G
G
Figura 7.28
2
2come un2 oscillatore
2
2 armonico,
2
⎢
⎥
⎢m −
dove
ora
.
=
w
!
!
⎜
⎟
=
y
y
+
+
−
,
!!
=
+
y
+
U = k1 Dℓ 1 + k2 Dℓ 2 V" I B Rk1Asen
sen
(7.11)
Z I Ob N+ Ik2M
E CaC xA ⎜N=I C ⎟kHeqE⎢x
223
n
2
2⎥ 1
2
1
Sistema
⎜
⎟
2
⎢ 4la rigidezza
⎥
Vibrazioni
4
dtè⎝così
∂y!2
⎢4
dt ⎝ ∂ y! ⎠ ⎢ 4
il modello
equivalente
definito,
keq è una
2
2
2
1 ⎠completamente
La rigidezza
equivalente
è data
dalla
7.4
( ℓ=1 +AEℓ 2 )dove
( ℓ 1 + ℓ 2mL
) equivalente
ℓ1 + ℓ 2 ⎥⎦
ℓ1 + ℓ 2
⎣ keq
⎦
⎣
⎦
di coordinate1
⎣
⎣
torsionali.
costante dipendente da parametri fisici
e geometrici
del problema.
L
lagrangiane
⎤
⎡
⎤
equivalente è così completamente
definito, la
equivalente
keqche
è una
⎛ ∂T
⎞ 2 ⎡m
X è l’ampiezza
dirigidezza
oscillazione,
è la2fase,
dal
con la
J –6 2si possono
⎤
⎡
m ricavare
–6
–6 J 2
⎥ y! confronto
alternative.
(7.23) Figura
⎛ ∂T ⎞ ⎡ m
A =problema.
32 d 10
JG
JG
dipendente da parametri fisici e geometrici del
d7.15
m
⎜⎜ m
⎟⎟ =–⎢ 2,9− 10G m ⎥=y! 10,59
+ ⎢ +10 mG
,
2
(
223 226 )
⎤
⎥ !!
y2 ,
(
)
2
⎥
(
)
(
)⎦
⎤
⎢
⎥
⎢
⎥ !!
2
2
7.30, si ha infatti che x =dtX cos(w
t
+
)
=
X
cosw
t
cos
–
X
senw
t
sen
,
da
cui
si
ricava:
⎢4
⎥
!!
Gru
y1 +
+
y , ⎝ ∂y! 2 ⎠ n ⎢⎣ 4 ( ℓ 1 + ℓ 2 ) n⎥⎦
⎜d’estremità
⎟ =⎢4 −
ℓ 1 trave
+ nℓ 2 ) ⎦ a mensola con massa
2
2
(
⎣ una
Esempio
7.2r
Vibrazioni
flessionali
di
Figura
7.15
!
⎥
⎢
⎥ 2
dt
∂
y
4
⎝
⎠
per
sollevamento:
2
da cui si ottiene la rigidezza equivalente
ℓ
+
ℓ
ℓ
+
ℓ
(
)
(
)
1
2
1
2
⎦
⎣
⎦
Gru
deformazione cavo. ⎣
∂U
∂U
Le energie cinetica e potenziale
sono
(7.33)
= k1 –y6w
,2 date=da:
k2 y 2
11
per
sollevamento:
1
w
0,∂y
59 × 10 nella
× 10 Pa Emilia
m 2,1regione
N
∂U Emilia, Bon∂U
∂y
Un forte evento
keq =sismico
=21,239
×Romagna,
105
1
2
= k1 y1 ,
= k 2 y2
deformazione
cavo. con epicentro tra Finale
2
1
m
m
⎛
⎞
⎛
⎞
∂ y1
∂ y2
! 2 massima
y! 1 + yla
– y! 1
y!deflessione
1
1
1
2
2
L’ampiezza X rappresenta
della1 molla
k che2in generale
dengo e Sant’Agostino
(comuni
⎟⎟ , U =di kModena
T = m ⎜⎜
y + k y e Ferrara),
⎟⎟ + J ⎜⎜in provincia
(7.22)avvenuto nella notte del
G
1* 1
2
2
2
2 ⎠ del2moto:
avviene
t2 le ⎝equazioni
⎝ ℓ 1 + ℓ 2 ⎠x(t ) = X e2x(t ) = 0,
riga 4cui
nell’istante
(può anche essere 0) si ottengono
da
cuimaggio
sidaottiene
la2012,
frequenza
20
dipropria
notevole
magnitudo
(5.9 Richter),l’energia
causòtotale
diversi dannit e alcune
vittime,
*
*
*
1
esempio kX ;7.11a.
del
sistema
queste
condizioni
è pari all’energia
potenziale
della
mollaFigura
utitra
quali7in.7 un
operaio
schiacciato
daldicrollo
di un
silos,
La probabile causa
del N
silesviluppino
necessari
per
le equazioni
⎡i termini
5 N
2
1,239 × 10 5
⎛
⎛ ×
⎞,239
⎞ ⎤Lagrange:
1
10
1
⎢ ⎜ mdelle 7.33
J del
J in direzione
⎜m
⎟ ⎥
crollo
fulal’oscillazione
terreno
orizzontale
(terremoto ondulatorio),
la quale m = 56,02Hz lizzando
prima
si ⎟dimostra
immediatamente
essa è pari all’energia
m
fn =
65 Hzche
⎢ ⎜ + fn = 2p ⎟⎡ ⎜ − ⎡ =⎤ 2211
2 ⎟ ⎥⎡ ,⎤
⎤
4
4
⎛
⎞
kg
1
2
π
1kg
⎡
⎤
⎞)1 m2 1 ( ℓJ +xdel
ℓoscillazioni
Jk 2 1
⎧⎪2 y ⎫⎪ ⎧0 ⎫ il crollo dovuto quasi sicura⎢ ⎝*
d
( ℓ ⎛⎜*+∂T
ha
indotto delle
forti
0⎥ kx
y =⎫⎪e1 successivamente
⎠⎢ ⎝+= k ⎢⎜ !ℓ0 ⎥⎟)y! silos
⎠+x⎥⎢⎧⎪2m⎥""
iniziale:
;
si
dimo!
(t ) + U
)
=
kX
+
m
x
+
=
E
!
⎟
=
y
−
,
⎢
⎥
0
0
0
in
(7.24)
+
=
⎨
⎬
⎨
⎬
⎨
⎬
Si applichi una
coppiaEM=alT⎢disco,
la (t
coppia
giace
sul
piano
ortogonale
all’asse
della
barra,
⎜
⎟ ⎢
⎥ ⎞ ⎥⎢ 4⎥"" 10 2 ⎢ ⎥ ⎥
dt ⎝ ∂y! ⎠2 secondaria
⎞ 4⎛ ( ℓ2AB
⎪⎩0in
⎪⎭ acciaio,
n ⎠della
⎪⎭(Pa
⎪⎩ y ⎪⎭fune
+⎢⎣=
ℓ⎝ w
ℓ ⎣ (trattasi
+0ℓ ) k2⎦a
⎦ystruttura
mente
ad7un’instabilità
(il
tema della stabilitàℓ elastica è
⎢ i⎛seguenti
Si considerino
di⎦guscio
una
⎦ E⎟1 =⎥⎣⎪⎩10
GJp a⎟⎣= 45°,
Jdati:
J3) Em,
m
m
229 esempio .9 ⎜
⎜
⎢
⎥
quindi
che
l’energia
totale
resta
costante.
−
+
la rotazionestra
risultante
è
data
da
dove
è
il
modulo
di
taglio,
E
il
G
=
=
M
q
il
modulo
di
Young
equivalente
è
molto
minore
di
quello
dell’acciaio,
per
considerare
il fatto
θM =
M M
⎡
⎤
⎡
⎤
⎜4
scopi
testo
e⎟ implica
studi
4Pa (trattasi
+)n )⎟ di
⎢ ⎜10del
⎥ mtipo superiore).
rino i seguenti dati: a = 45°,oltre
ABche
= 3gli
m,sezione
E1 = 10
in
acciaio,
11
2
J
ℓ ⎛ +∂Tℓ ⎞)di ⎠⎢una
ℓJ 2
+(1ℓnominale),
m⎝ fune
d(resistente
GJ
(
⎥
⎢
⎥
la
reale
non
è
quella
E
=
2,1
10
Pa,
A
=
100
mm
,
⎝
⎠
2p
(7.23)
p
Esempio
7.8r
Trave
a
mensola
con
massa
di
estremità
!
!
2
1
⎣libera
=oscillatore
+⎦ con
+ periodo
, , ciò vuol diy inerzia
modulo
di Young,
n di
il coefficiente
di ⎜⎜Poisson,
Jp il− momento
d’area
T⎥ y=della
è periodica
di Young equivalente
è molto
quello
considerare
il fatto
2dell’acciaio,
Il minore
semplice
modello
di⎟⎟per
Figura
7.11b,
estremamente
semplificato, permette di descri⎥dipur
⎢ sepolare
dtquesto
ALa
=risposta
2500
mm
. di
⎝ ∂y! ⎠ 11⎢⎣−4ζω
ℓ + ℓ ) ⎦ 22 ⎣ 4 ( ℓ + ℓ ) ⎦ wn
27.48 (
t
−ζω t
233 non Si
eq GJ
one reale resistente
è quella
nominale),
E
=
2,1
10
Pa,
A
=
100
mm
,
!d’estremip tdiametro
2
1
consideri
l’esempio
di
Figura
7.11,
il
silos
ha
un’altezza
di
circa
L
=
25
m,
un
di La deformazione
x(t)
=
Xe
sin(
1−
ζ
ω
t
+
φ
)
+
X̂
cos(
ω
−
ψ
) rigidezza.
x(t) = Xe
cos( 1− ζ 2 ω nt + φ ) + X̂ cos(ω t − ψ ) vere
qualitativamente
il
comportamento
dinamico
sistema.
kloeq
=del
sezione trasversale
barra,
lunghezza
barra;
la
rigidezza
torsionale
è
.
n si
re che
ladella
vibrazione
questo
caso
è
un
fenomeno
che
ripete
nel
tempo
con
una
certa
N
N
N
come
si vede
oralinla
la
matrice
di
massa
è
non
diagonale,
mentre
è
la
matrice
di
%
"
$$$$
#$$$$% "$$#$$
mm2.
7
D = 2,5
m e uno1spessore
della
di
s==8,13
2= mm,
si4ipotizzi
di,xestremità
Si4ottiene:
= 12,31∂U
m,
35,07°,
k1∂U
, k2 =una
5,25massa
keq = 2,63pari
107 .
klamiera
y , un
y 10
x
frequenza;
la capire
frequenza
èb==definita
come
numero
volte
che 10
un
certo
fenomeno
sim in
È banale
che
scegliendo
altroil
sistema
didicoordinate
lagrangiane
si ottengono
xk
x
px
D di
tà
una
trave
incastrata,
sotto
l’azione
di
una
forza
trasversale
F
applicata
all’estremità
m
m
∂y del disco,
∂y dette
“otto
s = 8 Mg
Detto J = arm
, (D(comunemente
= R/2)
d’inerzia
polare
N il momento
N tonnellate”).
N l’equazione del moto è:
G
2
G
2
1
2
2
G1
2
1
2
1
1
G
2
2
2
2
2
G1
2
2
n
1
1
1
2
2
2
G
2
1
G1
1
1
G
2
2
1
1
2
oa
2
2
2
1
2
n
2
p
4
7 esempio una frequenza
nell’unità
per
pari a 1000Hz implica che il fepiene.10
= 12,31 m, b =233 35,07°, k1 ripete
=riga 8,13
, k2di
= tempo:
5,25
, keq = 2,63 107 .
32generale
1
5
10
dal mmatrici
⎛ 2ζω ωm ⎞
m
>
7.2.3
1
w
=
k
/
J
Jq + keqq =Svolgimento
0;nomeno
e
la
pulsazione
naturale
.
n al secondo,
eq
s , il periodo è perciò
basso dunque iln periodo
⎜ moto:
⎟ è
ψlevolte
=GRADI
arctan
2DI
da cui si
si ripete
ottengono
equazioni
del
SISTEMA
A1000
DUE
LIBERTÀ
2
1000
3
EI
⎜
⎟
ω ω n è: armonico
⎝ 1−
⎠keq = 3 il, per
consideri
l’equazione
7.5, la
rigidezza
equivalente
calcolarla
occorre
l’inverso
della
frequenza.
Nel
caso dell’oscillatore
periodo
di oscillazione
Si hannoDI
iSiseguenti
risultati:
A A DUE GRADI
LIBERTÀ
L
Si consideri
un
sistema
meccanico
composto
da
due masse
puntiformi collegate tra
⎡ ⎛
⎤
⎛ T sezione trasversale
⎞ della
⎞
1 4 mediante
241 determinare
eq 7.65 momento
di4 Jinerzia
trattandosi
di una
–1della trave,
loro
telaio
molle
(Figura
l’attenzione
al moto
verti
⎢ ⎜m
⎥ èrestringa
J7.16).
r(t)
Mφ frequenza
– 8⎟ φ
libera
èeTalil=da
misura
della
[s
Hz],
da non
confondere
con
⎜4 m
⎟ Si
Gdi
G
2
pdue
D.B L’unità
p
×
4
10
3m
eri un sistema meccanico
composto
masse
puntiformi
collegate
tra
+
−
−⎥ω
7 4sezione,
⎢
=
−
=
cost=sezione
circolare
cava
si
ha
I
=
pR
s
dove
R
è
il
raggio
della
con
i
dati
forniti
si
ha:
f
2 ⎟gravità,
210
J
=
=
=
,
×
m
2
51327
cale
e
si
ometta
la
forza
di
cioè
si
consideri
il
moto
del
sistema
attorno
alla
⎜
⎜
⎟
n
Capitolo 7_meccanica.indd
T
p 219 4
4 al moto
⎡ k
+ ℓ32
ℓ 2vertielaio mediante molle
(Figura
7.16).
Si⎢di
restringa
l’attenzione
32
( ℓr(t)
)Tramite
0 ⎤ ⎪⎧di
y 1periodo
y 1 ⎪⎫la definizione
⎪⎫ ⎧ 0 ⎫ si può
Κφ( ℓ 1–+1].
1 pulsazione
2) ⎠ φ
⎝equilibrio
⎝ [rad/s
⎠ ⎥ ⎪⎧ ""
l’unità
di misura
della
1
posizione
statico.
1
2
(
)
⎢
⎥
(7.24)
⎨ ⎬=⎨ ⎬
⎢
⎥⎨ ⎬ +
⎛ 2,5⎞sistema
metta laCapitolo
forza di7_meccanica.indd
gravità, cioè si consideri
del
attorno
alla
m⎛⎞
–3
40
⎞0,01227
y 2 1⎭⎪ ⎢⎣m2p
211⎢ ⎛ il moto
k 2 ⎥⎦ ⎩⎪ y 2 ⎭⎪ ⎩⎪ 0 ⎭⎪
⎥ ⎩⎪=""
I
=
p
2
×
10
m
=
⎜
⎟
J
J
m
m
T
=
ricavare la relazione
che implica wn = 2pfn.
⎟ ⎜⎠ e +pulsazione:
⎟ ⎥
di equilibrio statico.
G
G
⎢ ⎜ − tra frequenza
⎝ 22
f n wn
Alluminio
Acciaio
2 ⎟
⎜4
⎟ ⎜4
3
⎢
(è:ℓ 1 + ℓ 2 ) ⎠ ⎝ ( ℓ 1 + ℓ 2 ) ⎠ ⎥⎦
⎣ ⎝
la rigidezza
equivalente
10
2,1 × 1011 Pa
7,6 × 10
Pa 7.6r Conservazione
Esempio
= 8,07692 × 1010 Pa
G=
= 2,90076 × 1010 Pa dell’energia G =
11
4 2(1 + 0,3)
2(1 + 0,31)
2
1
×
10
,
Pa
0,01227
m
N
come si vede
ora
la
di massa
è non
diagonale,
mentre
matrice di rigidezza.
Dimostrare
che la
7.30
rispetta
il principio
conservazione
keqsoluzione
= matrice
3
= di
485376
,1 lo è la dell’energia.
3
3
Capitolo 7_meccanica.indd 215
(
oa
)
p
ψ = arctan 2 2ζω ω n ,1− (ω ω n ) !!
r(t)
r(t)
φ Kφ
2
T
=−
= cost=-ω 2
T 13/03/13 16:46
φ Mφ
13/03/13 16:46
13/03/13 16:46
mr̈ = Fe + Fd
per componenti 420
si può riscrivere:
254 259 (8.19)
MECCANICA APPLICATA ALLE MACCHINE
x + cx! + kx = mw 2 a cos wt
⎪⎧ m!!
⎨
⎪⎩ m!!
y + c8y!.1 + ky = mw 2 a sen wt
esempio (8.20)
p
g
2
=w
g
2sen
2
p cos
distanza tra i piani di equilibratura: l=0,5m vmax = w
, vmin
(11.64)
w(t) g
Si definisca ora la funzione complessa w(t) = x(t) + j y(t) con j = 2–1;
sen questa
funzione nella
sua rappresentazione
piano
complesso, coincide 2con b.
ϕ =nel
30°
ϕ A = 30° 262 esercizio 2vettoriale
Si sommi la prima delle 8.20 alla seconda moltiplicata per j:
366 esercizio 6 Ladomanda 7 di uscita della catena si può valutare come segue: per un avansostituire Si/No con maggiore/minore velocitàjwt
media
mẅ
= mw2 a(e2) (a) +1cw
(b) (8.21)
(a)
(b)
372 esempio 1.1 kwuscita uscita (5) 2p
*
*
g
=
=
ω
t
zamento
di
un
passo
angolare
(che
avviene
in
un
tempo
t
)
deve
seτ τ0
riga 8 La 8.21 è380 un’equazione
differenziale
complessa
che si può studiare con izmetodi
Il
giunto
di
Cardano
(Figura
11.68)
permette
di
trasferire
il
moto
tra
due
Il
assi
giunto
di
Cardano
(Figura
11.68)
ω permette
visti nel Capitolo
7.
Vista
la
presenza
dello
smorzamento
ci
si
può
ridurre
allo
studio
guire un avanzamento
380 riga 10 ω 3R
z2 della catena di un passo p, se si definisce V velocità nominale
z2 di trasferire il moto tra due assi
3R
non
paralleliovvero
incidenti
in soluzione
un punto,
aventi
un
a 90°.
paralleli
Il
incidenti in un punto,
un
teoricamente inferiore non
teoricamente inferiore a 90°. Il
τ 2 =particolare:
= −angolo
τ 2 =aventi
= angolo
del solo moto
a regime,
della
w pz
z3 chepsi=collega
z3 che si collega ai due alberi attra*
giunto è composto essenzialmente
daωuna
crociera
ai
due alberi
giunto
attra-èche
composto
essenzialmente
daωuna
2si
R può
2 R crociera
V
=
della catena
scrivere
Vt
;
si
ricava
facilmente
.
Ricordando
– f)
w(t) = wportogonali
(t) = |W| ej(wttra
(8.22)
2p
verso due coppie
verso due coppie rotoidali
ortogonali2πtra loro e giacenti ognuna sui piani ortogonali
420 riga 5rotoidali
2 p loro e giacenti ognuna sui piani ortogonali
che
si
può
ricavare
la
fluttuazione
di
velocità
(picco-picco)
γ =
g=
agli assi degli alberi.
agli assi degli alberi. normalizzata
dove:
2
z
alla velocità nominale
V:
2
1.68
Figura 11.68
⎛w⎞
424 Fig. 11.68b a
⎜ ⎟
Cardano:
Giunto di Cardano:
2
⎛
⎞
w
mw a
⎝ n⎠
inematici
schemi cinematici
W =
=
v − vmin (8.23)
p⎜ 1
g⎟
Dv e realizzazioni.
2
2
azioni.
2
2
2
2 max
(11.65)
=
=
−
cotan
⎜
⎟
⎡
⎤
( k − w m ) + ( cw ) ⎢1 − ⎛ w ⎞ ⎥ + ⎛ 2zV w ⎞ V
z ⎜ sen g
2⎟
⎜ ⎟
⎜
⎟
⎝
⎠
2
⎢⎣ ⎝ w n ⎠ ⎥⎦ ⎝ w n ⎠
riga 8 ⎡ Figura 11.58
⎤
Nel caso in
si ha z = 12, il che comporta g = 30° e una fluttuazione
w ⎥
⎢ 3,45%.
di velocità del
2z
⎛ cw ⎞
⎢
wn ⎥
f = arctan2 ⎜
(8.24)
⎟ = arctan2 ⎢
2⎥
2
Figura 11.59
⎝k −w m⎠
⎛w⎞ ⎥
⎢
Fluttuazione
1− ⎜ ⎟
⎢⎣ ⎝ w n ⎠ ⎥⎦
della velocità
in una catena
(a)
(b)
che la velocità di rotazione
rulli.assume implicitamente
Si noti che la a8.22
del vettore
(a)
b è pari a quella
dell’albero
sia in modulo che segno; questo tipo di moto è detto
Whirl”. Si può dimostrare che il “Backward Synchronous Whirl”,
“Synchronous
cioè q = – w è possibile solo se nella 8.17 si assumono diverse rigidezze lungo x e y.
eccanica.indd 259
dd 424
(b)
(c)
13/03/13 16:48
(d)
(c)
Le maglie delle
catene silenziose, Figura(e)11.60, sono ancora
formate da piastrine
collegate tra loro mediante dei perni. In questo tipo di catene però il contatto con
la ruota dentata non avviene più attraverso il cilindro di collegamento come nelle
catene a rulli, ma sono le maglie stesse a impegnare la ruota dentata. Le maglie sono
dunque conformate in maniera da realizzare un ingranamento senza urti con la ruota
dentata (Figura 11.61). Per evitare elevate pressioni di contatto ogni maglia ha un
Capitolo 11_meccanica.indd 424
13/03/13 17:13
certo numero di piastrine; le piastrine esterne in genere non sono sagomate, e perciò
(d)
(e)
13/03/13 17:13












