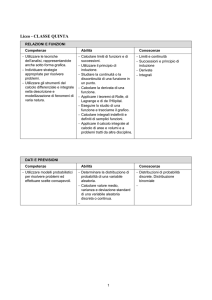
Dispense di Analisi 1 (2008-2009).nbp

Carlo Greco
Appunti di Analisi Matematica I
Carlo Greco
Appunti di Analisi Matematica I
2
Indice
1. Teoria degli insiemi ed elementi di logica ... 7
1. Nozioni introduttive sugli insiemi ... 7
2. Proposizioni e predicati ... 8
3. Quantificatori ... 9
4. Operazioni tra insiemi ... 10
5. Funzioni tra insiemi ... 12
6. Funzioni ingettive e surgettive ... 14
7. Funzioni composte e restrizioni ... 17
8. Insiemi finiti, infiniti e numerabili ... 19
9. Esercizi ... 22
2. Insiemi numerici ... 28
1. Insiemi numerici ... 28
2. Intervalli ... 31
3. Cenni sui numeri complessi ... 31
4. Esercizi ... 32
3. Funzioni e loro grafici ... 35
1. Il concetto di funzione ... 35
2. Altri esempi di funzioni ... 38
† Rette ... 38
† Potenza n-esima ... 38
† Parabole ... 39
† Radice n-esima ... 40
† Iperbole ... 41
† Funzioni definite "a pezzi". Funzione valore assoluto di x e funzione segno di x ... 41
† Traslazioni ... 43
3. Esercizi ... 44
4. Funzioni pari, dispari, periodiche ... 47
5. Operazioni con le funzioni ... 49
† Somma, prodotto e quoziente ... 49
† Relazione d'ordine ... 50
† Minoranti e maggioranti; funzioni limitate e illimitate ... 50
† Composizione di funzioni ... 51
† Codominio di una funzione; funzioni surgettive ed ingettive; funzioni inverse ... 52
6. Esercizi ... 56
7. Funzioni monotone ... 59
8. Successioni ... 61
9. Esercizi ... 63
4. Disequazioni razionali e irrazionali ... 65
1. Generalità sulle disequazioni ... 65
2. Disequazioni di primo e secondo grado ... 66
3. Esercizi ... 69
4. Disequazioni di grado superiore al secondo ... 70
† Caso generale: polinomi fattorizzati ... 70
† Caso generale: decomposizione in fattori ... 72
† Le biquadratiche ... 75
† Disequazioni del tipo xn < k, xn § k, xn > k, xn ¥ k. ... 76
5. Disequazioni razionali fratte ... 78
6. Sistemi di disequazioni ... 80
7. Disequazioni irrazionali ... 82
† Disequazioni del tipo
n
† Disequazioni del tipo
n
A@xD < B@xD oppure
A@xD > B@xD oppure
n
n
A@xD § B@xD ... 83
A@xD ¥ B@xD. ... 86
5. Funzioni elementari ... 90
1. La funzione esponenziale e la funzione logaritmo ... 90
† Funzione esponenziale ... 90
† Funzione logaritmo ... 92
2. Le funzioni trigonometriche e le loro inverse ... 94
† La misura in radianti di un angolo ... 94
† Le funzioni seno e coseno ... 95
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
3
† Le funzioni arcoseno e arcocoseno ... 98
† Le funzioni tangente e arcotangente ... 102
† Altre funzioni trigonometriche ... 104
† Periodicità delle funzioni trigonometriche ... 105
3. Esercizi ... 106
6. Disequazioni esponenziali, logaritmiche e trigonometriche ... 109
1. Disequazioni esponenziali ... 109
2. Disequazioni logaritmiche ... 111
3. Disequazioni trigonometriche ... 114
† Disequazioni trigonometriche elementari ... 114
† Disequazioni contenenti una sola funzione trigonometrica incognita ... 119
† Disequazioni di secondo grado in seno e coseno ... 120
† Disequazioni lineari in seno e coseno ... 121
4. Disequazioni con le funzioni trigonometriche inverse ... 123
5. Disequazioni col valore assoluto ... 124
6. Alcune disequazioni trascendenti ... 128
7. Disequazioni varie e calcolo del dominio di definizione di una funzione ... 130
7. Limiti di funzioni e successioni ... 136
1. Definizione di limite di una funzione ... 136
2. Esercizi ... 146
3. Funzioni che non ammettono limite ... 147
4. Limite a sinistra e a destra ... 148
5. Esercizi ... 150
6. La definizione generale di limite ... 151
7. Teoremi sui limiti ... 152
† Operazioni con i limiti ... 152
† Limiti di polinomi ... 155
† Limiti all'infinito di funzioni razionali ... 156
† Esercizi ... 157
† Funzioni continue ... 157
† La forma indeterminata b ê 0 ... 159
† Limiti delle funzioni razionali negli zeri del denominatore ... 160
† Esercizi ... 161
† Limiti di funzioni composte ... 162
† Limiti di alcune funzioni irrazionali ... 163
† Esercizi ... 164
8. Asintoti ... 164
9. Permanenza del segno, conservazione delle disuguaglianze e confronto ... 166
† Permanenza del segno e conservazione delle disuguaglianze ... 166
† Confronto ... 168
† Esercizi ... 169
10. Alcuni limiti notevoli ... 170
Sin@xD
† Il limite notevole limxØ0
= 1 e i limiti notevoli collegati ... 170
x
† Esercizi ... 172
† Prodotto di una funzione infinitesima per una limitata ... 173
† Somma di una funzione divergente e di una limitata ... 174
† Funzioni della forma f @xDg@xD e loro limiti ... 175
† Esercizi ... 177
11. Limiti di successioni ... 177
† Teoremi sui limiti delle successioni ... 178
1 n
† La successione II1 + Å M M e il numero di Nepero ... 179
n
n
limite notevole limxØ≤¶ I1 + Å1 M e i limiti notevoli collegati ... 182
12. Altri limiti notevoli ... 182
† Il
x
x
13. Esercizi ... 184
8. Funzioni continue ... 186
1. Funzioni continue e punti di discontinuità di una funzione ... 186
† Definizione di funzione continua e punti di discontinuità di una funzione ... 186
† Prolungamento per continuità di una funzione ... 189
† Esercizi ... 190
2. Minimo e massimo assoluto. Teorema di Weierstrass ... 191
3. Teorema degli zeri ... 194
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
4
4. Esercizi ... 198
9. Derivate ... 200
1. Definizione di derivata ... 200
2. Funzioni non derivabili; derivate a sinistra e a destra ... 203
3. Derivate di alcune funzioni; operazioni con le derivate ... 205
4. Esercizi ... 209
5. Derivate successive ... 209
6. Significato fisico della derivata ... 211
7. Tangenti e approssimazioni ... 212
8. Derivate delle funzioni elementari ... 214
† Derivata di xa ... 214
† Derivata di ax ... 214
† Derivata di Loga @xD e di Loga @ » x »D ... 215
† Derivate delle funzioni trigonometriche ... 215
† Derivate delle funzioni trigonometriche inverse ... 216
† Tabella delle derivate delle funzioni elementari ... 217
† Derivate di funzioni della forma f @xDg@xD ... 218
9. Esercizi ... 219
10. Calcolo dei limiti mediante la regola dell'Hôpital ... 219
11. Esercizi ... 222
10. Applicazioni delle derivate. Studio di grafici ... 224
1. Alcune applicazioni delle derivate ... 224
† Punti di minimo o massimo relativo ... 224
† Ricerca del minimo o del massimo assoluto ... 226
† Teoremi di Rolle, Lagrange; crescenza e decrescenza ... 227
2. Primi studi del grafico di una funzione ... 232
3. Concavità e convessità, flessi, studio dei punti angolosi e cuspidali ... 235
† Convessità, concavità e flessi ... 235
† Punti angolosi e cuspidali ... 238
† Esercizi ... 243
4. Studio di grafici ... 244
† Funzioni razionali e irrazionali ... 244
† Funzioni logaritmiche ed esponenziali ... 247
† Funzioni trigonometriche ... 251
† Funzioni varie ... 254
† Esercizi ... 257
11. Il problema dell'area. Integrali definiti ... 258
1. Cenni sulla misura secondo Peano-Jordan ... 258
2. Area del trapezoide e funzioni integrabili secondo Riemann ... 259
3. Esercizi ... 268
4. Proprietà dell'integrale ... 268
5. Esercizi ... 271
6. Primitive e teorema fondamentale ... 272
7. Esercizi ... 277
12. Integrali indefiniti ... 279
1. Integrali indefiniti immediati e integrazione per decomposizione ... 280
† Integrali indefiniti immediati ... 280
† Integrali indefiniti immediati generalizzati ... 281
† Integrazione per decomposizione ... 283
2. Esercizi ... 284
3. Integrazione per parti ... 285
4. Integrazione di alcune funzioni razionali fratte ... 288
† Integrali del tipo ‡
† Integrali del tipo ‡
† Integrali del tipo ‡
† Integrali del tipo ‡
Settembre 2008
1
a x2 +b x+c
q+p x
a x2 +b x+c
p x+q
a x2 +b x+c
q+p x
a x2 +b x+c
„ x, con D < 0 ... 289
„ x, con D < 0. ... 290
„ x, con D > 0. ... 291
„ x, con D = 0. ... 293
Carlo Greco
Appunti di Analisi Matematica I
† Integrali del tipo ‡
5
P@xD
a x2 +b x +c
„ x, con P@xD polinomio di grado maggiore o uguale a due ... 294
† Esercizi ... 295
5. Integrali particolari ... 295
6. Integrazione per sostituzione ... 298
7. Esercizi ... 301
8. Funzioni non integrabili elementarmente ... 301
13. Infinitesimi e Infiniti ... 303
1. Generalità sugli infinitesimi ... 303
2. Infinitesimi campione e ordine di infinitesimo ... 305
3. Generalità sugli infiniti ... 308
4. Infiniti campione e ordine di infinito ... 309
5. Esercizi ... 310
14. Integrali impropri ... 311
1. Funzioni limitate, intervallo @a, +¶@ ... 311
2. Funzioni limitate, intervalli D - ¶, aD, e D - ¶, +¶@ ... 317
3. Funzioni non limitate, intervalli D a, bD, @a, b@, o D a, b@ ... 319
4. Esercizi ... 322
15. La formula di Taylor ... 323
1. I polinomi di Taylor e la formula di Taylor col resto di Peano ... 323
2. Esercizi ... 327
3. Il test della derivata n-esima per i punti di minimo, massimo e flesso ... 328
4. La formula di Taylor con il resto di Lagrange ... 329
5. Esercizi ... 332
16. Indici ... 333
1. Indice analitico ... 333
2. Indice dei teoremi ... 336
3. Indice delle definizioni ... 337
4. Notazioni ... 338
Avvertenza sulle notazioni usate in questo testo
In questi appunti di Analisi Matematica le notazioni adoperate sono leggermente diverse da quelle standard; la ragione è
dovuta essenzialmente al programma con cui sono stati compilati. Ad esempio si usa la notazione f @xD per indicare le
funzioni, adoperando quindi le parentesi quadre, invece della notazione più usata che è f HxL. Anche i nomi delle funzioni
elementari sono leggermente diversi da quelli standard: il logaritmo in base ‰, ad esempio, viene indicato con Log@xD,
mentre di solito si indica con log x.
Particolare attenzione dovrà essere usata per le potenze delle funzioni elementari; ad esempio, per indicare il quadrato del
logaritmo di x usiamo il simbolo Log@xD2 invece della notazione consueta log2 x. Bisogna dunque prestare attenzione a non
confondere Log@xD2 con LogAx2 E, che, con le consuete notazioni si scriverebbe invece logIx2 M.
Al termine di queste dispense si trova un elenco in cui sono indicate tutte le principali differenze rispetto alle notazioni
consuete. E' opportuno consultare spesso questo elenco, in modo da non avere nessun dubbio sull'interpretazione dei
simboli.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
258
11 Il problema dell'area. Integrali definiti
In questo capitolo vedremo come definire la nozione di area di un sottoinsieme del piano, e studieremo come calcolarla,
introducendo il concetto di integrale definito e indefinito. Vedremo inoltre le applicazioni di tali concetti a problemi di
fisica e di meccanica.
1. Cenni sulla misura secondo Peano-Jordan
Supponiamo che A sia un sottoinsieme di 2 ; vogliamo associare a questo sottoinsieme un numero che ne esprima in modo
ragionevole l'estensione. Questo numero sarà chiamato area di A, oppure, in vista di future generalizzazioni al caso in cui
A sia un sottoinsieme di 3 , o, più in generale, di n , misura di A.
Se A è un rettangolo, un triangolo, o, più in generale, un poligono, cosa si debba intendere per area di A è noto dalla
geometria elementare. Nel caso in cui A sia invece un cerchio, si incontra una difficoltà essenziale, dovuta al fatto che un
cerchio, a differenza di un poligono, non è decomponibile in triangoli. Questa difficoltà può essere superata
"approssimando" dall'interno e dall'esterno il cerchio con figure geometriche di cui è nota l'area, ad esempio poligoni
regolari. Si trovano, in questo modo, due classi contigue di grandezze: quella delle aree dei poligoni inscritti, e quella delle
aree dei poligoni circoscritti al cerchio. Queste due classi contigue individuano un unico numero reale, che si assume, per
definizione, come area del cerchio.
In questo consiste, in sostanza, il metodo di esaustione, noto fin dall'antichità. Esso consente, nello stesso tempo, di
definire la nozione di area per un insieme non decomponibile in triangoli o in rettangoli, e di fornire un metodo pratico
per il calcolo approssimato di essa.
Una generalizzazione di questo metodo consente di definire l'area di figure piane molto più generali di un cerchio, ed è
basato sulla procedura di approssimare, sia dall'esterno che dall'interno l'insieme dato mediante "plurirettangoli", cioé
mediante unioni di un numero finito di rettangoli di 2 .
Diamo anzitutto le seguenti definizioni.
(Rettangolo)
Definizione 11.1.1
Si dice rettangolo di  2 il prodotto cartesiano di due intervalli limitati di  .
Per intervallo di  si intende un intervallo aperto, chiuso o semiaperto, eventualmente costituito anche da un solo punto.
L'area di un rettangolo R sarà indicata con » R », ed è, come al solito, il prodotto delle lunghezze dei lati.
Definizione 11.1.2
(Plurirettangolo)
Si dice plurirettangolo di  2 l'unione di un numero finito di rettangoli di  2 , a due a due internamente disgiunti.
L'insieme dei plurirettangoli di  2 si indica con 7 I 2 M.
Dunque un plurirettangolo è un insieme di 2 che può essere decomposto in un numero finito di rettangoli aventi a due a
due in comune, eventualmente, una parte del bordo (dunque senza che vi siano "sovrapposizioni" delle parti interne).
Definizione 11.1.3
(Area di un plurirettangolo)
Se P è un plurirettangolo di  2 , e se R1 , R2 , …, Rn è una sua decomposizione in un numero finito di rettangoli, per cui si
ha:
P = ‹ Rk ,
n
si dice area di P, e si indica con » P », la somma delle aree dei rettangoli R1 , R2 , …, Rn :
k= 1
» P » = ⁄ » Rk ».
n
k= 1
Osservazione. Se P è un plurirettangolo, in generale esistono infiniti modi di decomporre P nell'unione di un numero
finito di rettangoli. Se R1 , R2 , …, Rn , ed S1 , S2 , …, Sm sono due di queste decomposizioni, per cui:
P = Ê Rk = Ê Sk ,
n
m
k=1
k=1
si ha evidentemente che
Ê » Rk » = Ê » Sk »,
Settembre 2008
n
m
k=1
k=1
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
259
pertanto la definizione precedente di area di un plurirettangolo è lecita malgrado la non unicità della decomposizione.
Sia ora A un sottoinsieme limitato di 2 . Indichiamo con 7i HAL l'insieme di tutti i plurirettangoli di 2 contenuti in A
(l'indice i sta per interni), e con 7e HAL l'insieme di tutti i plurirettangoli di 2 che contengono A (l'indice e sta per esterni).
Definizione 11.1.4
(Insieme misurabile)
Sia A un sottoinsieme limitato di  2 ; se i due insiemi numerici costituiti dalle aree dei plurirettangoli interni ed esterni ad
A:
8 » P » » P œ 7i HAL< e 8 » P » » P œ 7e HAL<
sono contigui, l'insieme A si dice misurabile secondo Peano-Jordan, ed il loro elemento di separazione si dice misura
secondo Peano-Jordan (o semplicemente, nel caso bidimensionale, area) di A. In tal caso, la misura di A verrà indicata
con » A ».
La definizione appena data di area di un insieme appare del tutto naturale: anzitutto consente di recuperare la nozione di
area nota dalla geometria elementare, infatti i rettangoli, i triangoli, i poligoni ecc. ecc., sono tutti misurabili secondo
Peano-Jordan, e la loro misura coincide con quella già nota; analoga osservazione vale per l'area del cerchio.
La maggior parte degli insiemi che capita di considerare nelle applicazioni sono misurabili secondo Peano-Jordan; tuttavia
esistono anche insiemi che, invece, non lo sono.
Esempio 11.1.1
Sia A l'insieme dei punti del quadrato unitario a coordinate razionali:
A = 8Hx, yL œ @0, 1D µ @0, 1D » x œ , y œ <
Ebbene, l'insieme A non è misurabile, infatti gli unici plurirettangoli contenuti in A sono quelli costituiti da un numero
finito di punti, ed hanno area nulla, pertanto
8 » P » » P œ 7i HAL< = 80<.
D'altra parte, qualunque plurirettangolo contenente A deve contenere anche il quadrato @0, 1D µ @0, 1D che ha area 1,
pertanto l'insieme numerico 8 » P » » P œ 72 HAL< è costituito da numeri maggiori o uguali ad uno. Dunque tali insiemi
numerici non sono contigui.
2. Area del trapezoide e funzioni integrabili secondo Riemann
Nel paragrafo precedente abbiamo visto come è possibile definire la nozione di area per un sottoinsieme del piano; siamo
ora interessati a particolari sottoinsiemi del piano, chiamati trapezoidi.
Definizione 11.2.1
(Trapezoide)
Sia f : @a, bD Ø  una funzione positiva e limitata; si dice trapezoide di base @a, bD relativo alla funzione f , l'insieme:
T f = 8Hx, yL » x œ @a, bD, 0 § y § f @xD<.
Dunque il trapezoide T f non è altro che la parte di piano (limitata) compresa tra l'asse x e il grafico di f , come si vede in
figura:
Vediamo come è possibile (e se è possibile) individuare opportuni plurirettangoli contenuti in T f e contenenti T f atti ad
approssimare per difetto e per eccesso la sua area (ammesso che T f sia misurabile secondo Peano-Jordan).
Sia dunque f : @a, bD Ø  una funzione positiva e limitata. Suddividiamo poi l'intervallo @a, bD in n intervallini mediante i
punti x0 , x1 , ... xn , dove a = x0 < x1 < x2 < ... xn = b (questi punti non sono necessariamente equidistanziati). Indichiamo
con il simbolo c questa suddivisione dell'intervallo:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
260
c = 8x0 , x1 , ... xn <,
e indichiamo con S@a, bD l'insieme di tutte le possibili suddivisioni dell'intervallo @a, bD. Indichiamo ora con mi il minimo
assoluto della funzione f @xD in ciascuno degli intervallini @xi-1 , xi D della suddivisione fissata (ammesso che questo minimo
assoluto esista):
xœ@xi-1 ,xi D
mi =
min
f @xD.
Consideriamo ora i vari rettangolini @xi-1 , xi D µ @0, mi D; la loro unione è un plurirettangolo che indichiamo con P f @ cD:
Pf @ cD = Ê @xi-1 , xi D µ @0, miD.
n
i=1
Ciò che stiamo facendo è illustrato dal seguente grafico.
Ovviamente P f @ cD è un plurirettangolo "inscritto" in T f , la cui area approssima per difetto quella di T f . L'area del
plurirettangolo P f @ cD è:
sf @ cD = ‚ mi Hxi - xi-1 L.
n
i=1
La sommatoria precedente si chiama somma inferiore relativa alla suddivisione c.
Naturalmente l'approssimazione è tanto migliore quanto più fitta è la suddivisione c dell'intervallo @a, bD. Indichiamo con
A@ f D l'insieme numerico delle aree di tutti i plurirettangoli del tipo s f @ cD al variare di c nell'insieme delle suddivisioni
dell'intervallo @a, bD:
A@f D = 8sf @ cD » c œ S@a, bD<.
In modo analogo, posto:
xœ@xi-1 ,xi D
Mi = max
f @xD
(sempre ammesso che tale massimo assoluto esista in ciascuno degli intervallini @xi-1 , xi D), e posto:
Qf @ cD = Ê @xi-1 , xiD µ @0, MiD,
n
i=1
si ha un plurirettangolo "circoscritto" a T f :
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
261
la cui area è:
Sf @ cD = ‚ Mi Hxi - xi-1 L.
n
i=1
(La sommatoria precedente si chiama somma superiore relativa alla suddivisione c). Poniamo, di conseguenza,
B@f D = 8Sf @ cD » c œ S@a, bD<.
Dunque B@ f D è l'insieme delle aree di tutti i plurirettangoli circoscritti a T f . E' chiaro che i due insiemi numerici A@ f D e
B@ f D sono separati, nel senso che ogni plurirettangolo inscritto ha area minore o uguale ad ogni plurirettangolo
circoscritto. Se essi sono anche contigui, il trapezoide T f è misurabile secondo Peano-Jordan, e la sua misura (la sua area)
è, per definizione, l'elemento di separazione tra tali insiemi. In altri termini, è ora possibile dare la seguente definizione.
(Integrale secondo Riemann)
Definizione 11.2.2
Con le notazioni sopra introdotte, la funzione f : @a, bD Ø  si dice integrabile (secondo Riemann) se gli insiemi numerici
A@ f D e B@ f D sono contigui; in tal caso il loro elemento di separazione si chiama integrale (secondo Riemann) di f , e si
indica col simbolo:
b
Ÿa f @xD „ x
n
1
5.93319 < Ÿa f @xD„x < 15.7683
b
Esempio 11.2.1 ( f @xD = k )
Consideriamo il caso di una funzione costante, a costante valore k > 0, nell'intervallo @a, bD; in questo caso T f non è altro
che il rettangolo di base @a, bD e altezza k , cosicché la sua area è kHb - aL.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
262
11. Il problema dell'area. Integrali definiti
Vediamo di ritrovare questo risultato col metodo dei plurirettangoli inscritti e circoscritti. Suddividiamo l'intervallo in n
intervallini, e per ciascuno di essi consideriamo il minimo valore assunto dalla funzione; nel caso di una funzione costante,
si ha, ovviamente: mi = k , pertanto l'area del generico plurirettangolo inscritto è:
sf @ cD = ‚ mi Hxi - xi-1 L = ‚ k Hxi - xi-1 L = k ‚ Hxi - xi-1 L = k Hb - aL.
n
n
n
i=1
i=1
i=1
Dunque, ogni plurirettangolo inscritto ha sempre area uguale a kHb - aL; ciò è evidente dalla figura:
Dunque, l'insieme A@ f D delle aree dei plurirettangoli inscritti si riduce al solo elemento kHb - aL:
A@f D = 8k Hb - aL<.
In modo perfettamente analogo si verifica che anche l'insieme B@ f D è costituito dal solo numero kHb - aL:
B@f D = 8k Hb - aL<.
Dunque tali insiemi numerici sono ovviamente contigui, e il loro elemento di separazione non è altro che kHb - aL.
Adoperando la simbologia degli integrali, possiamo scrivere:
‡ k „ x = k Hb - aL.
b
Esempio 11.2.2 ( f @xD = x)
a
Consideriamo ora la funzione f @xD = x nell'intervallo @0, bD; in questo caso T f è un triangolo la cui area è
b2
2
.
Ritroveremo nuovamente questo risultato col metodo dei plurirettangoli inscritti e circoscritti. Suddividiamo l'intervallo in
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
263
11. Il problema dell'area. Integrali definiti
b
n
n intervallini, questa volta di uguale lunghezza Å ; si ha dunque:
b
xi = Å i, dove i = 0, 1, ..., n.
n
In ciascuno degli intervalli @xi-1 , xi D, il minimo di f è assunto nel primo estremo xi-1 , e vale proprio f @xi-1 D = xi-1 ; si ha
cioé mi = xi-1 :
Pertanto l'area del plurirettangolo inscritto è:
n
n
n
b2 n
b
b n b
sf @ cD = ‚ mi Hxi - xi-1 L = ‚ xi-1 Hxi - xi-1 L = ‚ xi-1 Å = Å ‚ Å Hi - 1L =
‚ Hi - 1L.
n
n i=1 n
n2 i=1
i=1
i=1
i=1
Ora, l'ultima sommatoria non è altro che la somma dei primi n - 1 interi naturali; poiché si ha, com'è noto:
1+2+3+∫+n-1=
abbiamo ottenuto, in definitiva:
sf @ cD =
I numeri s f @ cD = b2
n-1
2n
b2 n Hn - 1L
2
n
2
n Hn - 1L
= b2
2
,
Hn - 1L
2n
.
approssimano per difetto l'area del triangolo; passando al limite per n Ø +¶, si ottiene
b2
2
modo analogo, considerando le aree dei plurirettangoli circoscritti, e facendo tendere n Ø +¶, si ottiene ancora
Abbiamo dunque dimostrato che:
b
1 2
‡ x „x = Å b .
2
0
La formula ottenuta può essere facilmente generalizzata al caso di un integrale esteso all'intervallo @a, bD, infatti si ha:
‡ x „ x = area del triangolo di base @0, bD - area del triangolo di base @0, aD =
b
a
Esempio 11.2.3 ( f @xD = x2 )
b2
2
-
a2
2
.
Consideriamo infine la funzione f @xD = x2 nell'intervallo @0, bD; T f è ora la parte di piano al di sotto di una parabola:
Settembre 2008
. In
b2
.
2
Carlo Greco
Appunti di Analisi Matematica I
264
11. Il problema dell'area. Integrali definiti
La sua area non è nota dalla geometria elementare; vedremo tuttavia che, grazie al metodo dei plurirettangoli inscritti e
circoscritti, essa potrà essere calcolata.
b
n
Suddividiamo l'intervallo in n intervallini, di lunghezza uguale; prendiamo infatti xi = Å i, dove i = 0, 1, ..., n.
In ciascuno degli intervalli @xi-1 , xi D, il minimo di f è ancora assunto nel primo estremo xi-1 , e vale proprio f @xi-1 D = x2i-1 ;
si ha cioé mi = x2i-1 :
Pertanto l'area del plurirettangolo inscritto è:
n
n
n
b3 n
b
b n b2
2
sf @ cD = ‚ mi Hxi - xi-1 L = ‚ xi-1 2 Hxi - xi-1 L = ‚ xi-1 2 Å = Å ‚ Hi - 1L2 =
‚ Hi - 1L .
2
3
n
n
n
n
i=1
i=1
i=1
i=1
i=1
Ora, l'ultima sommatoria è la somma dei quadrati dei primi n - 1 interi naturali; poiché si ha:
1 + 22 + 32 + ∫ + Hn - 1L2 =
abbiamo ottenuto, in definitiva:
sf @ cD =
Passando al limite per n Ø +¶, si ottiene
b3 n Hn - 1L H2 n - 1L
3
n
6
n Hn - 1L H2 n - 1L
6
= b3
,
Hn - 1L H2 n - 1L
6 n2
.
b3
.
3
In modo analogo, considerando le aree dei plurirettangoli circoscritti, e facendo tendere n Ø +¶, si ottiene ancora
b3
3
.
Abbiamo dunque dimostrato che:
1 3
2
‡ x „x = Å b .
3
0
b
Ragionando come alla fine dell'esempio precedente, si ottiene immediatamente:
2
‡ x „ x = area del trapezoide di base @0, bD - area del trapezoide di base @0, aD =
b
a
b3
3
-
a3
3
.
Osserviamo ora che non tutte le funzioni sono integrabili; un famoso esempio di funzione non integrabile è fornito dalla
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
265
cosiddetta funzione di Dirichlet, che è definita nel modo seguente:
f @xD =
0 se x œ 
1 se x – 
Il grafico di questa funzione non è disegnabile in modo completo: esso consiste di infiniti punti densamente distribuiti sia
sull'asse x (quelli di ascissa razionale) sia sulla retta y = 1 (quelli di ascissa irrazionale).
y
1
x
La funzione di Dirichlet, sopra definita, non è integrabile; infatti, consideriamo l'intervallo @a, bD, e suddividiamolo
mediante i punti a = x0 , x1 , ..., xn = b, come al solito; in ciascuno degli intervalli @xi-1 , xi D cadono sia punti razionali
Esempio 11.2.4 (La funzione di Dirichlet)
che irrazionali, pertanto il minimo mi vale 0, e il massimo Mi vale 1; dunque:
sf @ cD = ‚ mi Hxi - xi-1 L = ‚ 0 Hxi - xi-1 L = 0,
n
n
i=1
i=1
Sf @ cD = ‚ Mi Hxi - xi-1 L = ‚ 1 Hxi - xi-1 L = ‚ Hxi - xi-1 L = b - a.
n
n
n
i=1
i=1
i=1
A@f D = 80<,
B@f D = 8b - a<.
Pertanto
Questi due insiemi numerici non sono contigui, quindi la funzione data non è integrabile.
La funzione dell'esempio precedente non è l'unica a non essere integrabile; si possono infatti immaginare molte altre
varianti dello stesso tipo; ad esempio, non è integrabile la funzione:
f @xD = :
x
se x œ 
2 x se x – 
il cui grafico è del tipo seguente:
y
x
Per fortuna, tuttavia, esistono vaste classi di funzioni integrabili, come ad esempio le funzioni continue e quelle monotone.
Teorema 11.2.1 (Integrabilità delle funzioni continue)
Una funzione continua in @a, bD è integrabile sullo stesso intervallo.
Teorema 11.2.2 (Integrabilità delle funzioni monotone)
Una funzione monotona in @a, bD è integrabile sullo stesso intervallo.
Esempio 11.2.5
Consideriamo la funzione f : @-1, 3D Ø  così definita:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
x-1
266
se - 1 § x < 1
f @xD = 2 - 2 x + x
2
x-2 +3
se 1 § x § 2
se 2 < x § 3
y
3
2
1
-2
-1 -1
-2
1
2
3
x
Essa è monotona (strettamente crescente) nell'intervallo considerato, pertanto è integrabile per il teorema sull'integrabilità
delle funzioni monotone.
Osservazione. La definizione di integrale come elemento di separazione tra gli insiemi A@ f D e B@ f D, non deve far passare
in secondo piano l'idea principale, che consiste, in sostanza, nel suddividere l'intervallo @a, bD in piccoli sottointervalli
@xi-1 , xi D in ciascuno dei quali la funzione f @xD (che si chiama funzione integranda) può essere considerata,
approssimativamente, costante e nel sommare le aree dei rettangolini ottenuti. In altri termini, l'idea principale consiste
"nell'affettare e sommare".
Osservazione. Quando abbiamo considerato la somma inferiore s f @ cD (risp. la somma superiore S f @ cD), abbiamo, in
sostanza, supposto che la funzione f @xD fosse costante, a costante valore mi (risp. Mi ) su ciascuno degli intervalli @xi-1 , xi D.
intervallino; ciò è comodo solo perché, in tal caso, i numeri s f @ cD e S f @ cD forniscono delle approssimazioni per difetto e
In realtà, non è importante che tale valore costante sia necessariamente il minimo mi o il massimo Mi di f su tale
per eccesso di Ÿa f @xD „ x.
b
Invece del minimo o del massimo, avremmo potuto scegliere il valore di f in qualsiasi punto ci dell'intervallino @xi-1 , xi D.
In tal caso l'area del rettangolino di base @xi-1 , xi D sarebbe stata f @ci D Hxi - xi-1 L, e la somma delle aree sarebbe stata:
sf @ cD = ‚ f @ci D Hxi - xi-1 L
n
Hsomma di CauchyL.
i=1
Tale numero s f @ cD fornisce ancora una approssimazione di Ÿa f @xD „ x, ma non è possibile sapere a priori se per difetto o
b
per eccesso.
In particolare, se, ad esempio, prendiamo ci = xi-1 , si ha la situazione illustrata in figura:
Come si vede, alcuni dei rettangolini sono contenuti nel trapezoide T f , altri no.
Nella successiva animazione è possibile fissare una certa suddivisione dell'intervallo @a, bD, e scegliere poi
successivamente i punti ci in quattro modi diversi:
1°) ciascun ci coincide col primo estremo dell'intervallo @xi-1 , xi D;
2°) ciascun ci coincide col secondo estremo dell'intervallo @xi-1 , xi D;
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
267
11. Il problema dell'area. Integrali definiti
3°) ciascun ci è preso uguale al punto medio dell'intervallo @xi-1 , xi D;
4°) ciascun ci è preso a caso nell'intervallo @xi-1 , xi D.
n
4
Nuova suddivisione
Nuovi ci
ci = xi-1 ci = xi
Scelta:
ci =
xi-1 +xi
2
xi-1 § ci §xi
Osservazione. Il simbolo Ÿa f @xD „ x di integrale riflette l'idea fondamentale di "affettare e sommare". Infatti, se @x, x + „ xD
b
è un generico intervallino della suddivisione, di lunghezza "infinitesima" „ x e se scegliamo di prendere il valore di f nel
primo estremo di tale intervallo, l'area del rettangolino corrispondente è f @xD „ x; il simbolo Ÿa (che non è altro che una S
stilizzata) esprime il fatto che si stanno sommando le "aree infinitesime" f @xD „ x.
b
Osservazione. Poiché Ÿa f @xD „ x rappresenta un numero (un'area) la variabile x che compare nel simbolo di integrale è una
b
variabile "apparente"; essa può essere sostituita da un qualsiasi altro simbolo senza che il valore dell'integrale cambi:
Ÿa f @xD „ x = Ÿa f @tD „ t = Ÿa f @qD „ q, ∫.
b
b
b
Abbiamo introdotto il concetto di integrale partendo dal problema dell'area; tuttavia, se la funzione f @xD ha qualche
significato fisico, anche Ÿa f @xD „ x può rappresentare una grandezza fisicamente significativa.
b
Esempio 11.2.6 (Spazio percorso)
Un punto materiale si muove su una retta con velocità proporzionale al tempo: v@tD = k t; il grafico della velocità in
funzione del tempo è quindi una retta:
v
a
b
t
Vogliamo calcolare lo spazio percorso tra l'istante iniziale t = a e l'istante finale t = b; se la velocità fosse costante,
basterebbe moltiplicarla per il tempo trascorso: spazio = velocità µ Hb - aL; poiché non è costante, suddividiamo l'intervallo
@a, bD in tanti intervallini (ad esempio di uguale lunghezza) in ciascuno dei quali la velocità si può supporre costante; nel
generico intervallino @ti-1 , ti D possiamo supporre che essa sia uguale a v@ti-1 D; di conseguenza, lo spazio percorso in tale
intervallo temporale, è circa v@ti-1 D Hti - ti-1 L; la somma di tali spazi è:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
268
11. Il problema dell'area. Integrali definiti
sv @ cD = ‚ v@ti-1 D Hti - ti-1 L;
n
i=1
passando al limite per n Ø +¶, si ottiene lo spazio totale come integrale della velocità nell'intervallo @a, bD:
spazio = ‡ v@tD „ t.
b
a
Terminiamo con un'ultima osservazione. Abbiamo introdotto il concetto di funzione integrabile nel caso di funzioni
f : @a, bD Ø  limitate e positive; in questo caso la somma inferiore e quella superiore hanno il chiaro significato di aree di
plurirettangoli inscritti o circoscritti al trapezoide T f ; se invece la funzione data è negativa in @a, bD, sia la somma inferiore
che quella superiore assumono valori negativi:
sf @ cD = ⁄ mi Hxi - xi-1 L § ⁄ Mi Hxi - xi-1 L = Sf @ cD § 0,
n
n
i=1
i=1
questo perché, per una funzione negativa, si ha mi § Mi § 0. E' allora naturale interpretare i numeri negativi s f @ cD ed S f @ cD
ancora come aree di trapezoidi, ma contate negativamente in quanto tali trapezoidi si trovano al di sotto dell'asse x.
Conseguentemente, anche l'elemento di separazione tra le somme inferiori e quelle superiori potrà essere interpretato
ancora come l'area di un trapezoide, ma cambiata di segno in quanto il trapezoide si trova al di sotto dell'asse x. In
definitiva, la definizione di funzione integrabile si estende immediatamente alle funzioni che non sono sempre positive in
@a, bD.
3. Esercizi
E' data la funzione f @xD = 1 - x2 , con x œ @-1, 1D; considerata la suddivisione
Esercizio 11.3.1
(plurirettangoli)
c = 8-1, -0.8, 0.2, 0.5, 1<
dell'intervallo @-1, 1D, calcolare le somme:
sf @ cD = ‚ f @xi-1 D Hxi - xi-1 L
4
i=1
sf @ cD = ‚ mi Hxi - xi-1 L
4
i=1
Esercizio 11.3.2
(def. di integrale)
Adoperando la definizione, calcolare i seguenti integrali:
‡ H2 x + 1L „ x;
3
1
2
‡ Ix + 1M „ x.
1
0
4. Proprietà dell'integrale
Il seguente teorema riassume le principali proprietà dell'integrale.
Teorema 11.4.1 (Proprietà dell'integrale)
Siano f , g : @a, bD Ø  due funzioni limitate integrabili. Allora:
1°) (linearità) Se c1 e c2 sono due costanti, la combinazione lineare c1 f @xD + c2 g@xD è integrabile, e si ha:
Ÿa Hc1 f @xD + c2 g@xDL „ x = c1 Ÿa f @xD „ x + c2 Ÿa g@xD „ x.
2°) (additività) Se x0 œ D a, b@, allora si ha:
b
b
b
Ÿa f @xD „ x = Ÿa 0 f @xD „ x + Ÿx f @xD „ x.
b
3°) (monotonia 1) Se f § g in @a, bD, allora si ha:
Settembre 2008
x
b
0
Carlo Greco
Appunti di Analisi Matematica I
269
11. Il problema dell'area. Integrali definiti
Ÿa f @xD „ x § Ÿa g@xD „ x.
4°) (monotonia 2) Se @a , b D Õ @a, bD, e se f ¥ 0, allora si ha:
b
b
Ÿa f @xD „ x § Ÿa f @xD „ x.
5°) (maggiorazione) La funzione » f @xD » è integrabile e si ha:
b
b
… Ÿa f @xD „ x … § Ÿa … f @xD … „ x.
b
b
Non dimostriamo il teorema precedente, ma ci limitiamo ad osservare che le proprietà 2°), 3°) e 4°) hanno un'immediata
interpretazione geometrica, come si vede dai seguenti grafici:
Ÿa f @xD„x + Ÿx0 f @xD„x
Ÿa f @xD„x § Ÿa f @xD„x
b
b
x0
y
b
y
a
x0
b
x
a
a
b
b
x
Esempio 11.4.1
Ÿ1 I Å2 x2 - 3 xM „ x. Si ha infatti:
Adoperando la proprietà di linearità dell'integrale, e gli integrali che già conosciamo, possiamo, ad esempio, calcolare
2 1
‡
2
1
2
23 13
22 12
29
1 2
1 2
Å x - 3 x „ x = Å ‡ x2 „ x - 3 ‡ x „ x = 4
-3
=
3
3
2
2
6
2
2 1
1
Dalla proprietà di linearità dell'integrale segue, in particolare, che:
‡ -f @xD „ x = -‡ f @xD „ x.
b
b
a
a
Poiché le funzioni f @xD e - f @xD sono simmetriche rispetto all'asse x, si ottiene da tale formula l'interpretazione geometrica
dell'integrale di una funzione f : @a, bD Ø  negativa in @a, bD: esso non è altro che l'area, cambiata di segno, della regione
di piano (al di sotto dell'asse x) compresa tra il grafico di f e l'asse delle x.
Esempio 11.4.2
Calcolare
‡
5
x
-5 1 + x4
„ x.
Non è necessario eseguire alcun calcolo: infatti, poichè la funzione integranda è dispari, l'area al si sopra dell'intervallo
@0, 5D è uguale a quella al di sopra dell'intervallo @-5, 0D:
y
0.4
0.2
-5
-0.2
-0.4
-0.6
5
x
Pertanto:
‡
5
x
-5 1 + x4
Esempio 11.4.3
Calcolare
Settembre 2008
„ x = 0.
Carlo Greco
Appunti di Analisi Matematica I
11. Il problema dell'area. Integrali definiti
‡
270
2p
Sin@xD „ x.
0
Anche in questo caso basta osservare il grafico:
y
p
x
2p
per concludere che
‡
2p
Sin@xD „ x = 0.
0
Un'altro teorema importante è il teorema della media.
Teorema 11.4.2 (Della media)
Sia f : @a, bD Ø  una funzione continua, e siano m ed M il minimo ed il massimo assoluto di f in @a, bD. Si ha allora:
Esiste inoltre c œ @a, bD tale che:
mHb - aL § Ÿa f @xD „ x § M Hb - aL.
b
Ÿa f @xD „ x = f @cD Hb - aL.
b
Anche questo teorema ha un'immediata interpretazione geometrica; infatti, osservando che m Hb - aL e M Hb - aL non è altro
che l'area dei due rettangoli nella figura seguente:
è evidente che l'area del trapezoide T f è compresa tra m Hb - aL e M Hb - aL. E' pure evidente che, scegliendo
opportunamente il punto c œ @a, bD, l'area del rettangolo tratteggiato in figura finirà per uguagliare l'area di T f .
y
M
f @cD
m
a c
c1
b
x
Ÿa f@xD„x < f@cDHb-aL
b
Dimostrazione del teorema della media. 1°) Poiché m ed M sono il minimo ed il massimo assoluto di f @xD, si ha
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
271
11. Il problema dell'area. Integrali definiti
m § f @xD § M in @a, bD; per la prima proprietà di monotonia dell'integrale, integrando i tre membri della diseguaglianza
essa si conserva:
‡ m „ x § ‡ f @xD „ x § ‡ M „ x.
b
b
a
b
a
Ricordando che Ÿa k „ x = kHb - aL, si ha la prima formula del teorema.
a
b
2°) Dalla formula già dimostrata si ha immediatamente:
m§
cioé, posto y0 =
b
1
Ÿ f @xD „ x,
b-a a
‡ f @xD „ x § M,
b
1
b-a
a
si ha y0 œ @m, M D. Ricordando che, per il teorema di Bolzano l'intervallo @m, M D non è
altro che il codominio di f @xD, cioé l'insieme dei suoi valori, si ha, appunto, che esiste c œ @a, bD tale che
f @cD =
‡ f @xD „ x,
b
1
b-a
a
da cui la seconda formula del teorema. à
Il numero
b
1
Ÿ f @xD „ x
b-a a
si dice valor medio della funzione f @xD nell'intervallo @a, bD.
Esempio 11.4.4 (Velocità media)
Un punto si muove lungo una retta con velocità v@tD = 10 t2 (lo spazio è misurato in Km e il tempo in ore). Calcolare lo
spazio percorso dopo 2h e 30m, e la sua velocità media.
Lo spazio percorso è dato dall'integrale:
spazio = ‡
5ê2
0
v@tD „ t = ‡
5ê2
0
10 t2 „ t = 10 ‡
5ê2
0
1 5
t2 „ t = 10 µ Å Å
3 2
3
=
625
12
La velocità media è data da:
5ê2
1
‡
0
5ê2
2 625 125
v@tD „ t = Å
=
= 20.83 = Km ê h.
6
5 12
5. Esercizi
Esercizio 11.5.1
(additività)
Spiegare perché
‡
2p
Cos@xD „ x = 0.
0
Esercizio 11.5.2
(stima)
Dimostrare che
‡ Sin@xD „ x < p ;
p
0
p
1
p
p
„x < Å ;
Å <‡
2
4
0 3 + Sin@xD
‡
0
Settembre 2008
1
5
3 + ‰x
„ x > 0.
= 52.08 = Km.
Carlo Greco
Appunti di Analisi Matematica I
Esercizio 11.5.3
272
11. Il problema dell'area. Integrali definiti
(media)
Dimostreremo in seguito che
‡
1
p
„x = Å .
2
+1
1
-1 x2
Determinare il valore (o i valori) di c œ @0, 1D in modo che si abbia:
‡
1
1
-1 x2
+1
„ x = 2 f @cD.
Interpretare poi geometricamente il risultato ottenuto.
Riprendiamo i risultati ottenuti nel secondo paragrafo integrando nell'intervallo @a, bD le tre funzioni f @xD = k , g@xD = x,
6. Primitive e teorema fondamentale
h@xD = x2 ; abbiamo ottenuto:
‡ k „ x = k Hb - aL.
b
a
‡ x „x =
b2
2
‡ x „x =
b3
b
-
2
a
b
a
3
a2
2
.
a3
-
3
.
Fissiamo l'attenzione, ad esempio, sul terzo integrale; consideriamo la funzione G@xD =
x3
3
, e osserviamo quanto segue:
2
‡ x „ x = G@bD - G@aD.
b
G '@xD = x3 ,
e
a
La funzione G@xD si chiama primitiva o antiderivata di x3 , e la formula precedente dice che il valore dell'integrale definito
Ÿa x2 „ x è dato dalla differenza tra i valori assunti dalla primitiva G@xD della funzione integranda x2 negli estremi
b
dell'intervallo di integrazione.
La stessa circostanza si presenta anche per il primo ed il secondo integrale. Infatti si ha:
‡ k „ x = G@bD - G@aD;
b
prendendo G@xD = k x :
G '@xD = k,
e
a
prendendo G@xD =
x2
2
‡ x „ x = G@bD - G@aD.
b
:
G '@xD = x,
e
a
Vedremo tra poco che queste formule valgono per "qualsiasi" funzione integranda f @xD, e forniscono il principale metodo
per il calcolo effettivo degli integrali definiti, che verrà quindi effettuato mediante la ricerca di una primitiva della funzione
integranda. Ad esempio, supponendo che quanto detto sopra valga anche per l'integrale:
‡
0
1
2x
x +1
2
„ x,
si potrà procedere nel modo seguente:
1°) si cerca una primitiva G@xD della funzione integranda; in questo caso prendiamo G@xD = LogAx2 + 1E, dato che:
G '@xD =
2°) scriviamo la formula fondamentale:
Settembre 2008
2x
x +1
2
.
Carlo Greco
Appunti di Analisi Matematica I
273
11. Il problema dell'area. Integrali definiti
‡
1
2x
x2 + 1
0
„ x = G@1D - G@0D = Log@2D.
Dunque:
‡
0
1
2x
x +1
2
„ x = Log@2D.
Approfondiamo ora le considerazioni precedenti, e iniziamo col dare la seguente definizione.
(Primitiva o antiderivata)
Definizione 11.6.1
Sia f : X Ø  una funzione definita in un intervallo X di  ; una funzione derivabile G : X Ø  si dice primitiva o
antiderivata di f se, per ogni x œ X si ha G'@xD = f @xD.
Esempio 11.6.1
La funzione G@xD = 3 x + 2 + Å1 è una primitiva della funzione f @xD = 3 x
1
x2
, infatti G '@xD = 3 -
1
x2
.
Esempio 11.6.2
La funzione G@xD = ArcTanAx2 E è una primitiva della funzione f @xD =
2x
x4 +1
, infatti G '@xD =
2x
x4 +1
.
Osserviamo ora che, se G@xD è una primitiva di f @xD, anche tutte le funzioni G@xD + c, dove c è una costante, sono primitive
di f , infatti D@G@xD + cD = G '@xD = f @xD. Ad esempio, le funzioni
x3
3
,
x3
3
+ 1,
x3
3
- 3.4, ... sono tutte primitive della stessa
funzione x2 . Viceversa, due primitive della stessa funzione differiscono per una costante; più precisamente, si ha il
seguente teorema.
Teorema 11.6.1 (Differenza di due primitive)
Sia X un intervallo di  , e siano F@xD e G@xD due primitive della stessa funzione f : X Ø  . Esiste allora una costante
c œ  , tale che F@xD = G@xD + c.
j'@xD =F '@xD - G '@xD = f @xD - f @xD = 0. Per il teorema sulle funzioni a derivata nulla, la funzione j@xD è costante
Dimostrazione.
Consideriamo
la
j@xD = F@xD - G@xD;
funzione
la
sua
derivata
è
nulla,
infatti
sull'intervallo X , dunque esiste c œ , tale che j@xD = c, cioé tale che F@xD - G@xD = c, da cui la tesi. à
Abbiamo considerato fino adesso integrali definiti su un intervallo @a, bD, quindi con a < b; è però opportuno, per un
motivo che vedremo tra poco, dare significato al simbolo Ÿa f @xD „ x anche nel caso in cui a ¥ b, in modo che si possano
b
considerare integrali definiti come i seguenti:
3
‡ x „ x, ‡ Sin@xD „ x, ecc. ecc.
2
0
p
5
Si pone, a questo scopo,
‡
x2
f @xD „ x =
-Ÿx 1 f @xD „ x
2
se x1 > x2
0
se x1 = x2
x
x1
Dunque si ha, ad esempio:
3
3
‡ x „ x = -‡ x „ x = 2
5
5
2
‡
4
4
x4
1 + x6
53
3
-
23
3
= -39,
„ x = 0,
ecc. ecc.. Molte delle proprietà dell'integrale definito enunciate precedentemente valgono anche nel caso in cui a ¥ b; ad
esempio la linearità, la proprietà additiva e il teorema della media, come si potrebbe verificare facilmente.
Con tale convenzione, possiamo dare la seguente fondamentale definizione.
Definizione 11.6.2
(Funzione integrale)
Sia X un intervallo di  sia a œ X , e sia f : X Ø  una funzione continua. La funzione F : X Ø  così definita:
x
F@xD = Ÿa f @tD „ t
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
274
11. Il problema dell'area. Integrali definiti
Dunque, se a < x, F@xD non è altro che l'area del trapezoide di base @a, xD relativo alla funzione f . Se invece a > x, F@xD è
si dice funzione integrale.
l'area del trapezoide di base @x, aD cambiata di segno. Si noti che, in ogni caso, F@aD = Ÿa f @tD „ t = 0.
a
Esempio 11.6.3
Sia f @xD =
x2
4
; la funzione F@xD = Ÿ1
x x2
4
„ t è una funzione integrale di f @xD. In questo caso, è facile calcolare esplicitamente
tale funzione; si ha infatti:
F@xD = ‡
1 3
1 x3 13
1 x
=
„ t = Å ‡ t2 „ t = Å
Ix - 1M.
4
3
12
4 3
4 1
x t2
1
Nella seguente figura si vede il grafico di f @xD =
x2
4
.
y
x
Il grafico della funzione F@xD =
1
12
Ix3 - 1M è invece il seguente:
y
2
1
-3
-2
a=1
-1
1
2
x
-1
Ad esempio, F@2D rappresenta l'area del trapezoide relativo alla funzione f , di base @1, 2D; in effetti, dalla figura precedente
si vede che tale area è all'incirca uguale a 59 mm2 , e, d'altra parte, F@2D =
1
12
I23 - 1M =
7
º 0.583.
Si ha poi, ovviamente, F@1D = 0, mentre F@-2D rappresenta l'area del trapezoide di base l'intervallo @-2, 1D, cambiata di
segno. Tale area è uguale (come si vede contando i quadratini) all'incirca a 76 mm2 . Il calcolo conferma questo conto,
infatti
F@-2D =
1
12
12
IH-2L3 - 1M = - Å = -0.75.
Esercizio 11.6.1
3
4
(Funzione integrale)
Nei seguenti grafici, osservare come varia l'area al variare di x; osservare, in particolare, quando è positiva, negativa,
quando cresce e quando decresce al crescere di x.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
x
-2
F@xD = Ÿa f @xD„x
f @xD
y
x
y
x
x a
x
x
x a
-2
F@xD = Ÿa f @xD„x
f @xD
y
a x
Settembre 2008
275
11. Il problema dell'area. Integrali definiti
x
y
x
a x
x
Carlo Greco
Appunti di Analisi Matematica I
276
x
-2
F@xD = Ÿa f @xD„x
f @xD
y
a
x
y
x
x
a
x
x
Nel seguente grafico, osservare come varia la funzione integrale F@xD al variare della funzione f @xD; in particolare,
Esercizio 11.6.2
osservare cosa accade alla funzione f @xD in corrispondenza dei minimi e dei massimi di F@xD.
x
Reset
F@xD = Ÿa f @xD„x
f @xD
y
x
y
x
a x
a x
x
Il seguente fondamentale teorema mostra la relazione che sussiste tra la funzione integrale F@xD, che abbiamo definito
precedentemente, e la funzione f @xD.
Teorema 11.6.2 (Funzione integrale)
Sia X un intervallo di  sia a œ X , e sia f : X Ø  una funzione continua. La funzione integrale
x
F@xD = Ÿa f @tD „ t
è una primitiva di f @xD, si ha cioé F '@xD = f @xD.
In un esempio precedente abbiamo calcolato esplicitamente la funzione integrale ), ottenendo F@xD =
effetti: F '@xD =
1
12
3 x2 =
x2
4
1
12
Ix3 - 1M. Si ha, in
. Il teorema sulla funzione integrale afferma che ciò è vero per qualsiasi funzione f @xD.
Dimostrazione del teorema sulla funzione integrale. Fissiamo un x0 œ X , e calcoliamo il rapporto incrementale:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
277
F@xD - F@x0 D
x - x0
0
Ÿa f @tD „ t - Ÿa f @tD „ t
x
=
x - x0
Ÿa f @tD „ t + Ÿx0 f @tD „ t
a
x
x
*
=
x - x0
Ÿx0 f @tD „ t
x
**
=
x - x0
(l'uguaglianza * è dovuta al fatto che, per definizione, Ÿx f @tD „ t = -Ÿa 0 f @tD „ t, mentre la ** deriva dalla proprietà
x
a
0
additiva dell'integrale). Osserviamo ora che, per il teorema della media, esiste c, appartenente all'intervallo di estremi x0 ed
x, tale che:
‡ f @tD „ t = f @cD Hx - x0 L.
x
x0
Dunque:
Ÿx0 f @tD „ t
x
=
x - x0
f @cD Hx - x0 L
x - x0
= f @cD.
Per x Ø x0 si ha c Ø x0 e quindi, data la continuità di f in x0 , si ha f @cD Ø f @x0 D. Pertanto:
F'@x0 D = lim
F@xD - F@x0 D
x - x0
xØx0
= lim f @cD = f @x0 D,
cØx0
e il teorema è dimostrato. à
Vale infine il seguente fondamentale teorema.
Teorema 11.6.3 (Fondamentale del calcolo integrale)
Sia f : X Ø  una funzione continua definita nell'intervallo X di  , e sia G@xD una sua primitiva; per ogni a, b œ X , si
ha:
b
Ÿa f @xD „ x = G@bD - G@aD.
Dimostrazione. Fissiamo a, b œ X , e consideriamo la funzione integrale F@xD = Ÿa f @tD „ t; essa è una primitiva di f ,
x
pertanto, per il teorema sulla differenza di due primitive, deve differire da G@xD per una costante: esiste quindi c œ  tale
che F@xD = G@xD + c, cioé:
‡ f @tD „ t = G@xD + c.
x
a
Ponendo x = a nella precedente espressione, si ha:
0 = ‡ f @tD „ t = G@xD + c,
a
a
da cui c = -G@aD. Dunque Ÿa f @tD „ t = G@xD - G@aD, e, in particolare, ponendo x = b, si ha la tesi del teorema. à
x
Il teorema precedente costituisce la chiave di volta per il calcolo degli integrali definiti, e pone il problema della ricerca
delle primitive di una data funzione.
Esempio 11.6.4
Calcolare il seguente integrale:
‡
pê2
Cos@xD „ x.
-pê2
La funzione Sin@xD è, ovviamente, una primitiva di Cos@xD, e anzi, tutte le primitive di Cos@xD sono del tipo Sin@xD + c, al
variare di c œ . Posto G@xD = Sin@xD, il teorema fondamentale assicura che:
p
p
p
p
Cos@xD „ x = GB Å F - GB- Å F = SinB Å F - SinB- Å F = 1 - H-1L = 2.
2
2
2
2
-pê2
‡
pê2
Terminiamo osservando che, per brevità, si usa scrivere G@bD - G@aD = @G@xDDba , e quindi, ad esempio, osservando che
4
una primitiva di x :
Settembre 2008
x5
5
è
Carlo Greco
Appunti di Analisi Matematica I
278
4
‡ x „x = B
2
-1
x5
5
F =
b
a
25
5
-
H-1L5
5
=
33
5
.
7. Esercizi
Esercizio 11.7.1
(Primitive)
Trovare una primitiva delle seguenti funzioni: 2 x,
1
x2
, Sin@xD, 2 +
1
x2 +1
.
Basandosi sul seguente grafico di f @xD, tracciare un grafico approssimativo di F@xD = Ÿ-1 f @tD „ t.
Esercizio 11.7.2
(Funzione integrale)
x
y
x
a = -1
Basandosi sul seguente grafico di f @xD, tracciare un grafico approssimativo di F@xD = Ÿ0 f @tD „ t.
Esercizio 11.7.3
(Funzione integrale)
x
y
a = -1
Settembre 2008
x
Carlo Greco
Appunti di Analisi Matematica I
279
12. Integrali indefiniti
12 Integrali indefiniti
Nel capitolo precedente abbiamo visto la definizione di integrale definito, e il teorema fondamentale del calcolo integrale,
che fornisce un metodo efficiente per il calcolo degli integrali definiti mediante la formula:
‡ f @xD „ x = G@bD - G@aD,
b
a
a patto di conoscere una "antiderivata" G@xD della funzione integranda f @xD. In questo capitolo vedremo come calcolare,
appunto, le primitive, ossia le antiderivate, di alcune semplici funzioni.
Se f @xD è una funzione definita e continua in un certo intervallo X , l'insieme delle sue primitive si denota col simbolo:
‡ f @xD „ x,
che si dice integrale indefinito di f @xD.
Ad esempio, se f @xD = x2 , una sua primitiva è
esse sono del tipo:
x3
3
x3
; poiché la altre primitive di f @xD = x2 differiscono per una costante da
x3
,
+ C , dove, appunto, C è un numero reale arbitrario. L'insieme di tutte le primitive di f @xD = x2 è
dunque la famiglia ad un parametro di funzioni
3
x3
3
3
+ C , al variare di C in . Il grafico di queste funzioni è il seguente.
y
x
Il tratto più spesso indica la funzione
x3
(che si ottiene dalla formula
x3
+ C prendendo C = 0), le altre curve si ottengono
dando a C altri valori. Per definizione, questo insieme di funzioni si indica con il simbolo Ÿ x2 „ x, cioé si pone:
3
2
‡ x „x =
x3
3
3
+ C.
Dunque, l'integrale indefinito di una certa funzione f @xD è l'insieme di tutte le primitive di quella funzione, e non bisogna
confonderlo con l'integrale definito, il cui significato geometrico è quello di un'area, cioé di un numero, e non certo di un
insieme di funzioni.
Calcolare un integrale indefinito è dunque sinonimo di trovare tutte le primitive di una data funzione, e tra poco
vedremo come calcolare gli integrali indefiniti più semplici.
Osserviamo infine che, per definizione, vale la formula:
‡ f '@xD „ x = f @xD + C,
cioé, ovviamente, l'integrale indefinito di una derivata è la funzione stessa, più una costante additiva.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
280
12. Integrali indefiniti
1. Integrali indefiniti immediati e integrazione per decomposizione
In questa sezione studieremo gli integrali definiti immediati, e una prima regola di integrazione indefinita che si chiama
integrazione per decomposizione.
ü Integrali indefiniti immediati
La tavola delle derivate delle funzioni elementari, letta in senso inverso, fornisce già una prima tavola di integrali
indefiniti, che chiameremo immediati. Infatti, sapendo, ad esempio, che
D[Sin[x]] = Cos[x],
conosciamo anche tutte le primitive della funzione Cos@xD, che sono: Sin@xD + C . In altri termini, abbiamo calcolato
l'integrale indefinito Ÿ Cos@xD „ x, e possiamo scrivere:
‡ Cos@xD „ x = Sin@xD + C.
In modo analogo si procede con le altre funzioni elementari, e si ha:
1L Ÿ xa „ x =
x1+a + C Hse a ∫ -1L
1
1+a
2L Ÿ Åx „ x = Log@ » x »D + C
1
3L Ÿ ‰x „ x = ‰x + C
4L Ÿ ax „ x =
ax
Log@aD
+C
5L Ÿ Sin@xD „ x = -Cos@xD + C
6L Ÿ Cos@xD „ x = Sin@xD + C
7L ‡
8L Ÿ
9L ‡
1
„ x = ArcSin@xD + C
1-x2
1
„ x = ArcTan@xD + C
1+x2
1
Cos@xD2
„ x = Tan@xD + C
Esempio 12.1.1
Calcolare l'integrale indefinito Ÿ x3 „ x;
Si deve utilizzare la prima formula, con a = 3:
1 4
3
‡ x „ x = Å x + C.
4
Esempio 12.1.2
Calcolare l'integrale indefinito Ÿ 1 „ x;
Anche in questo caso utilizziamo la prima formula con a = 0, dato che x0 = 1. Si ha:
1 1
‡ 1 „ x = Å x + C = x + C.
1
Si solito l'integrale Ÿ 1 „ x si scrive, più semplicemente: Ÿ „ x.
Esempio 12.1.3
Calcolare l'integrale indefinito Ÿ
Essendo
1
2
x = x1ê2 , possiamo utilizzare la prima formula con a = Å :
‡
Settembre 2008
x „ x;
x „x = ‡ x2 „x =
1
Å
1
1
1+ Å
1
1 + Å2
x
2
2
2
+ C = Å x3ê2 + C = Å x
3
3
x + C,
Carlo Greco
Appunti di Analisi Matematica I
281
12. Integrali indefiniti
cioé:
‡
2
x „x = Å x
3
x + C.
Esempio 12.1.4
Calcolare l'integrale indefinito ‡
Essendo
1
3
1
3
„ x;
x
= x-1ê3 , utilizziamo la prima formula con a = - Å :
1
3
x
‡
1
3
„x = ‡ x
1
1
-Å
3
„x =
x
1-
1
1- Å
1
Å3
x
3
3 Å2
3
+ C = Å x3 + C = Å
2
2
3
x2 + C,
cioé:
‡
1
3
3
„x = Å
2
x
3
x2 + C.
ü Integrali indefiniti immediati generalizzati
Dalla regola di derivazione delle funzioni composte abbiamo che, ad esempio:
D[Sin[j[x]]] = Cos[j[x]] j'[x],
e analogamente per le altre funzioni elementari. Si ottiene così:
1L D@j@xDa D = a j@xDa-1 j'@xD
2L D@Log@ » j@xD »DD =
1
j@xD
3L D@‰j@xD D = ‰j@xD j'@xD
j'@xD
4L D@aj@xD D = aj@xD Log@aD j£ @xD
5L D@Sin@j@xDDD = Cos@j@xDD j'@xD
6L D@Cos@j@xDDD = -Sin@j@xDD j'@xD
1
7L D@ArcSin@j@xDDD =
j'@xD
1-j@xD2
8L D@ArcTan@j@xDDD =
9L D@Tan@j@xDDD =
1
1+j@xD2
1
Cos@j@xDD2
j '@xD
j'@xD
Dalla precedente tabella, che possiamo chiamare delle derivate delle funzioni elementari generalizzate, si ottiene la
seguente tavola dei cosiddetti integrali indefiniti immediati generalizzati:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
282
12. Integrali indefiniti
1L Ÿ j@xDa j '@xD „ x =
2L Ÿ
1
j@xD
1
1+a
j@xD1+a + C Hse a ∫ -1L
j'@xD „ x = Log@ » j@xD »D + C
3L Ÿ ‰j@xD j'@xD „ x = ‰j@xD + C
4L Ÿ aj@xD j'@xD „ x =
aj@xD
Log@aD
+C
5L Ÿ Sin@j@xDD j'@xD „ x = -Cos@j@xDD + C
6L Ÿ Cos@j@xDD j'@xD „ x = Sin@j@xDD + C
7L ‡
8L ‡
9L ‡
1
j'@xD „ x = ArcSin@j@xDD + C
1-j@xD2
1
1+j@xD2
j'@xD „ x = ArcTan@j@xDD + C
1
Cos@j@xDD2
j'@xD „ x = Tan@j@xDD + C
I seguenti esempi illustrano l'uso degli integrali indifiniti immediati generalizzati.
Esempio 12.1.5
Vogliamo calcolare l'integrale indefinito:
2
‡ CosAx E 2 x „ x.
Se poniamo j@xD = x2 , possiamo utilizzare la 6) della tabella precedente, e ottenere immediatamente:
2
2
‡ CosAx E 2 x „ x = SinAx E + C.
Esempio 12.1.6
Calcolare:
Sin@xD
Cos@xD „ x.
‡ ‰
Questa volta utilizziamo la 3); si ha immediatamente:
Sin@xD
Cos@xD „ x = ‰Sin@xD + C.
‡ ‰
Esempio 12.1.7
Calcolare:
‡
3 x2
1 + x6
„ x.
Possiamo scrivere:
‡
3 x2
1 + x6
„x = ·
1
1 + Ix M
3 2
DAx3 E „ x;
utilizzando la 8) si ha immediatamente:
‡
Esempio 12.1.8
Calcolare:
Settembre 2008
3 x2
1 + x6
„x = ·
1
1 + Ix M
3 2
DAx3 E „ x = ArcTanAx3 E + C.
Carlo Greco
Appunti di Analisi Matematica I
283
12. Integrali indefiniti
2
‡ Sin@xD Cos@xD „ x.
Si ha:
2
2
‡ Sin@xD Cos@xD „ x = ‡ Sin@xD D@Sin@xDD „ x;
utilizzando la 1) con a = 2, si ha:
1
2
2
3
‡ Sin@xD Cos@xD „ x = ‡ Sin@xD D@Sin@xDD „ x = Å Sin@xD + C.
3
ü Integrazione per decomposizione
Dalla linearità della derivata si deduce immediatamente la seguente formula, che si dice di integrazione per
decomposizione:
‡ Hc1 f @xD + c2 g@xDL „ x = c1 ‡ f @xD „ x + c2 ‡ g@xD „ x.
In particolare, abbiamo le seguenti due formule:
‡ c f @xD „ x = c ‡ f @xD „ x,
‡ Hf @xD + g@xDL „ x = ‡ f @xD „ x + ‡ g@xD „ x.
Cioé: una costante (rispetto ad x) può essere "portata fuori" dall'integrale, e l'integrale di una somma è uguale alla somma
degli integrali.
La formula di integrazione per decomposizione consente di aumentare di molto la portata delle formule viste sopra per gli
integrali indefiniti immediati e generalizzati, come è illustrato nel seguente esempio.
Esempio 12.1.9
Vogliamo calcolare l'integrale indefinito:
2
‡ CosAx E x „ x.
Un integrale simile a questo, e precisamente l'integrale Ÿ CosAx2 E 2 x „ x è stato già calcolato in uno degli esempi
precedenti, servendoci della formula:
‡ Cos@j@xDD j '@xD „ x = Sin@j@xDD + C.
Infatti, nel caso dell'integrale Ÿ CosAx2 E 2 x „ x, il ruolo della funzione j@xD è svolto da x2 . Nel caso attuale, invece, manca,
nell'integrale, la costante 2! per ovviare a questo inconveniente, ricorriamo al trucco di moltiplicare e dividere per due
l'integrale, portando poi il fattore 2 sotto il segno di integrale:
1
1
1
1
2
2
2
2
2
‡ CosAx E x „ x = Å 2 ‡ CosAx E x „ x = Å ‡ CosAx E 2 x „ x = Å ISinAx E + CM = Å SinAx E + C.
2
2
2
2
C
2
C
2
Si noti che, nell'ultimo passaggio, non abbiamo scritto Å , dato che, essendo C una costante arbitraria, scrivere Å oppure
soltanto C è del tutto indifferente. In definitiva abbiamo ottenuto:
1
2
2
‡ CosAx E x „ x = Å SinAx E + C.
2
Esempio 12.1.10
Calcolare l'integrale indefinito:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
284
12. Integrali indefiniti
‡
Log@xD
x
x „ x.
+
Questa volta osserviamo anzitutto che:
‡
Log@xD
x
x „x = ‡
+
Log@xD
x
„x +‡
x „x
per la formula di decomposizione. Il primo dei due integrali è un integrale immediato generalizzato, infatti, ricordando che
1
x
D@Log@xDD = Å , possiamo scrivere:
‡
Log@xD
x
„ x = ‡ Log@xD D@Log@xDD „ x;
ricordando poi che:
a
‡ j@xD j'@xD „ x =
1
1+a
Hse a ∫ -1L
j@xD1+a + C
e quindi, in particolare:
1
2
‡ j@xD j'@xD „ x = Å j@xD + C,
2
si ha:
‡
Log@xD
x
1
„ x = ‡ Log@xD D@Log@xDD „ x = Å Log@xD2 + C,
2
e così il primo dei due integrali è calcolato. Il secondo è immediato, essendo:
‡
x „x = ‡ x2 „x =
1
Å
1
1+
1
1
Å2
x
1+ Å
2
2 Å3
2
+ C = Å x2 + C = Å x
3
3
x + C.
Pertanto l'integrale dato sarà uguale alla somma dei due risultati ottenuti, cioé:
‡
Log@xD
x
+
x „x = ‡
Log@xD
x
„x +‡
1
2
x „ x = Å Log@xD2 + C + Å x
2
3
1
2
x + C = Å Log@xD2 + Å x
2
3
x + C.
Si noti che, anche in questo caso, abbiamo scritto, nell'ultimo passaggio, C e non 2 C , sempre perché C è una costante del
tutto arbitraria.
2. Esercizi
Esercizio 12.2.1
Calcolare i seguenti integrali indefiniti immediati:
‡ 3 „ x; ‡ x „ x; ‡
3
x „ x; ‡ x
4
x „ x; ‡
„ x; ‡
1
5
x
1
x
„ x.
x
Esercizio 12.2.2
Calcolare i seguenti integrali indefiniti immediati generalizzati:
‡
·
Sin@xD Cos@xD „ x; ‡
Sin@xD „ x; ‡
-1
2
1 - Cos@xD
Settembre 2008
1
1+x 2
1
1
Å „ x;
1 + Log@xD x
2
1
x
„ x; ‡
1
1
Tan@xD Cos@xD2
„ x.
Carlo Greco
Appunti di Analisi Matematica I
285
12. Integrali indefiniti
Esercizio 12.2.3
Adoperando il metodo di decomposizione, calcolare i seguenti integrali indefiniti:
‡
1 + x3
·
1
x
„ x; ‡
5
1
1+
x
4
Cos@xD3 Sin@xD „ x;
„ x;
3
x
‡
1
2x+1
„ x.
Esercizio 12.2.4
Adoperando il metodo di decomposizione, calcolare i seguenti integrali indefiniti:
‡
x3 + 2
x-3
‡
„ x Hdividere il numeratore per il denominatoreL;
x+1
x2 + 1
‡
„ x; ‡
1
4 + x2
‰x
1 + ‰2 x
„ x;
‡
„ x; ‡
5 ‰x
1 + ‰x
1 - x4 + x
1 + x2
„ x;
„ x.
Esercizio 12.2.5
Calcolare i seguenti integrali indefiniti immediati.
Nuova tavola Reset
Esercizio 12.2.6
Calcolare i seguenti integrali indefiniti immediati generalizzati.
Nuova tavola Reset
Esercizio 12.2.7
Utilizzando gli integrali indefiniti immediati (anche generalizzati) e l'integrazione per decomposizione, calcolare i seguenti
integrali indefiniti.
Nuova funzione Soluzione Reset
3. Integrazione per parti
Consideriamo la formula di derivazione del prodotto:
D[f[x]g[x]] = f'[x]g[x] + f[x]g'[x];
da essa si deduce che:
f[x]g'[x] = D[f[x]g[x]] - f'[x]g[x].
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
286
12. Integrali indefiniti
Passando all'integrale indefinito, e ricordando che Ÿ D@ f @xD g@xDD „ x = f @xD g@xD + C , si ha la seguente formula, che viene
detta formula di integrazione per parti:
‡ f @xD g'@xD „ x = f @xD g@xD - ‡ f '@xD g@xD „ x.
La formula di integrazione per parti consente dunque di calcolare l'integrale indefinito di una funzione che si presenta
come prodotto di una funzione f @xD per una derivata g '@xD, purché si sappia calcolare l'integrale indefinito di f '@xD g@xD.
In molti casi questo secondo integrale è molto più semplice di quello dato, e quindi l'uso della formula risulta conveniente.
Il fattore f @xD prende il nome di fattore finito, mentre g '@xD si dice fattore differenziale. In pratica spesso conviene
assumere, come fattore differenziale, quello del quale si sa calcolare facilmente una primitiva, e, come fattore finito, quello
la cui derivata è più semplice, come si vede nel seguente esempio.
Esempio 12.3.1
Calcolare l'integrale:
‡ x Log@xD „ x.
La funzione da integrare, cioé x Log@xD, si presenta come il prodotto delle due funzioni x e Log@xD; non possiamo utilizzare
né gli integrali immediati, né quelli generalizzati. Volendo adoperare la formula di integrazione per parti, dobbiamo
anzitutto decidere quale dei due fattori dobbiamo prendere come fattore finito e quale come fattore differenziale, tenendo
presente che, del fattore differenziale dobbiamo essere capaci di calcolare una primitiva. Nel nostro caso, dobbiamo
prendere x come fattore differenziale, dato che, al momento, non siamo in grado di calcolare una primitiva di Log@xD.
Invece una primitiva di x è, ovviamente,
x2
2
. Scriviamo dunque:
‡ x Log@xD „ x = ‡ Log@xD x „ x =
‡ Log@xD DB
x2
2
F „ x = Log@xD
x2
2
- ‡ D@Log@xDD
x2
2
„ x.
L'ultimo integrale si calcola immediatamente:
‡ D@Log@xDD
1 x2
x
1
„x = ‡ Å
„ x = ‡ Å „ x = Å x2 + C,
2
x 2
2
4
x2
pertanto si ha:
‡ x Log@xD „ x = Log@xD
x2
1
- Å x2 + C.
2
4
Esempio 12.3.2
Calcolare l'integrale:
‡ x Cos@xD „ x.
In questo caso possiamo assumere sia x che Cos@xD come fattori differenziali, infatti conosciamo sia una primitiva di x (e
cioé
x2
)
2
che di Cos@xD (cioé Sin@xD). Assumiamo come fattore differenziale, ad esempio, Cos@xD. Si ha:
‡ x Cos@xD „ x = x Sin@xD - ‡ D@xD Sin@xD „ x =
= x Sin@xD - ‡ Sin@xD „ x = x Sin@xD + Cos@xD + C.
Dunque il risultato cercato è:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
287
‡ x Cos@xD „ x = x Sin@xD + Cos@xD + C.
Osserviamo che, se avessimo invece assunto x come fattore differenziale, avremmo dovuto effettuare i seguenti passaggi:
‡ x Cos@xD „ x =
‡ Cos@xD x „ x = Cos@xD
x2
2
- ‡ D@Cos@xDD
x2
2
„ x = Cos@xD
x2
2
- ‡ H-Sin@xDL
x2
2
„ x = Cos@xD
1
+ Å ‡ Sin@xD x2 „ x.
2
2
x2
Come si vede, l'ultimo integrale, cioé Ÿ Sin@xD x2 „ x, è più complicato di quello di partenza! Questo fatto ci obbliga a
scegliere invece Cos@xD come fattore differenziale, come abbiamo fatto sopra.
Esercizio 12.3.1
Utilizzando la formula di integrazione per parti, calcolare i seguenti integrali indefiniti:
x
‡ x Sin@xD „ x; ‡ x ‰ „ x.
Talvolta può essere opportuno applicare la formula di integrazione per parti assumendo 1 come fattore differenziale, come
si vede nel seguente esempio.
Esempio 12.3.3
Calcolare l'integrale:
‡ ArcSin@xD „ x.
Scriviamo:
‡ ArcSin@xD „ x =
‡ ArcSin@xD 1 „ x = ‡ ArcSin@xD D@xD „ x = ArcSin@xD x - ‡ D@ArcSin@xDD x „ x = ArcSin@xD x - ·
1
x „ x.
1-x
2
Ora, l'ultimo integrale è un integrale immediato generalizzato, infatti:
·
1
1 - x2
1
-Å ·
2
1
1 - x2
1
x „x = - Å ·
2
H-2 xL „ x =
1
1 - x2
1
1
1
1
1 1
-Å
1- Å
Å
DA1 - x2 E „ x = - Å ‡ I1 - x2 M 2 DA1 - x2 E „ x = - Å
I1 - x2 M 2 + C = -I1 - x2 M 2 + C.
2
2 1 - Å1
2
In definitiva:
‡ ArcSin@xD „ x = ArcSin@xD x +
1 - x2 + C.
Esercizio 12.3.2
Utilizzando la formula di integrazione per parti, calcolare i seguenti integrali indefiniti:
‡ ArcCos@xD „ x; ‡ ArcTan@xD „ x; ‡ Log@xD „ x.
Talvolta è necessario applicare più volte la formula di integrazione per parti, come nel seguente esempio.
Esempio 12.3.4
Calcolare il seguente integrale:
2 x
‡ x ‰ „ x.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
288
Ovviamente conviene assumere ‰x come fattore differenziale:
2 x
2
x
2 x
x
‡ x ‰ „ x = ‡ x D@‰ D „ x = x ‰ - ‡ 2 x ‰ „ x.
Come si vede, applicando una prima volta la formula di integrazione per parti, l'integrale dato si è semplificato (perché la
derivata di x2 è 2 x), ma l'ultimo integrale da calcolare, cioé Ÿ 2 x ‰x „ x, non è ancora immediato.
A quest'ultimo, tuttavia, è possibile applicare ancora la formula di integrazione per parti:
x
x
x
x
x
x
‡ 2 x ‰ „ x = 2 ‡ x ‰ „ x = 2 Kx ‰ - ‡ ‰ „ xO = 2 Hx ‰ - ‰ L + C,
pertanto:
2 x
2 x
x
x
x 2
‡ x ‰ „ x = x ‰ - 2 Hx ‰ - ‰ L + C = ‰ Ix - 2 x - 1M + C.
Esercizio 12.3.3
Calcolare i seguenti integrali indefiniti:
3
x
2
‡ I2 x + 1M ‰ „ x; ‡ x Sin@xD „ x;
2
3
‡ x Log@xD „ x; ‡ Log@xD „ x; ‡
x
Cos@xD2
„ x.
Esempio 12.3.5
Applicando più volte l'integrazione per parti, è possibile calcolare integrali del tipo Ÿ xn ‰x „ x ed altri simili, come si vede
nella tabella seguente.
n
Funzione:
1
Exp Log Sin Cos
x
x
‡ x ‰ „ x = Hx - 1L ‰
Esempio 12.3.6
Anche integrali di funzioni tipo ArcSin@xDn possono essere calcolati, in linea di principio, mediante successive integrazioni
per parti.
n
Funzione:
1
Log ArcSin ArcCos
‡ Log@xD „ x = -x + x Log@xD
4. Integrazione di alcune funzioni razionali fratte
In questa sezione vogliamo mostrare come si calcolano gli integrali del tipo:
‡
P@xD
a x2 + b x + c
„ x,
dove P@xD è un polinomio. Inizieremo a considerare, anzitutto, il caso in cui P@xD è una costante oppure un polinomio di
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
289
primo grado; se il grado di P@xD è maggiore o uguale a 2, si effettua la divisione dei polinomi, come vedremo in seguito.
Il metodo per il calcolo di tali integrali dipende dal segno del discriminante D del trinomio di secondo grado al
denominatore, pertanto dobbiamo distinguere diversi casi.
ü Integrali del tipo ‡
1
‚ x, con D < 0
a x2 +b x+c
Gli integrali indefiniti del tipo:
‡
1
ax +bx+c
2
„ x, con D < 0,
si riconducono facilmente all'integrale:
‡
1
„ x = ArcTan@xD + C,
x +1
2
o, meglio, all'integrale indefinito immediato generalizzato:
‡
1
j@xD2 + 1
j'@xD „ x = ArcTan@j@xDD + C.
Per fare ciò si adoperano semplici trasformazioni della funzione integranda, e, in qualche caso, si adopera il metodo del
completamento del quadrato, che consente di scrivere il denominatore come somma di due quadrati.
Esempio 12.4.1
Calcolare l'integrale:
‡
1
x +2
2
„ x.
In questo caso basta scrivere:
‡
1
„x = Å ·
2
x +2
1
2
1
„x = Å ·
2
+1
J
1
x2
2
1
x
2
N +1
2
2 ·
1
„x = Å
2
J
1
N +1
2
x
2
1
„x =
2
2
2
ArcTanB
x
F + C.
2
Esempio 12.4.2
Calcolare l'integrale:
‡
1
3x +4
2
„ x.
In questo caso l'integrale dato ha già, come denominatore, una somma di quadrati.
Per ricondurlo all'integrale ‡
1
j@xD2 +1
‡
1
=Å
4
2
3
·
K
1
3x +4
2
1
3
2
j'@xD „ x = ArcTan@j@xDD + C , possiamo scrivere:
3
2
xO + 1
2
„x = ·
3
4 I Å4
1
„x =
2
3
1
x2 + 1M
·
K
„x = ·
1
3
2
4 K
DB
2
xO + 1
1
3
2
3
2
2
„x =
xO + 1
1
xF „ x =
2
ArcTanB
3
3
2
xF + C.
Esempio 12.4.3
Calcolare l'integrale:
‡
1
x +2x+2
2
„ x.
Il trinomio x2 + 2 x + 2 ha discriminante negativo, quindi può essere scritto come somma di due quadrati. A tale scopo
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
290
basta completare x2 + 2 x aggiungendo e togliendo 1; si ha così:
‡
1
x2 + 2 x + 2
„x = ‡
x2 + 2 x + 1 - 1 + 2
Quest'ultimo è un integrale immediato generalizzato del tipo ‡
‡
1
x +2x+2
2
„x = ‡
1
„x = ‡
1
Hx + 1L2 + 1
Hx + 1L2 + 1
„ x.
j '@xD „ x, che è uguale a ArcTan@j@xDD + C . Dunque:
j@xD2 +1
1
1
„ x = ArcTan@x + 1D + C.
Esempio 12.4.4
Calcolare l'integrale:
‡
1
4x -4x+4
2
„ x.
Anche in questo caso D < 0; usando il metodo del completamento del quadrato, scriviamo:
‡
„x = ‡
1
4x -4x+4
2
1
4x -4x+1-1+4
2
A questo punto, sempre per ricondurci all'integrale ‡
‡
1
Å ·
3
1
H2 x-1L2
3
+1
1
„x = Å ·
3
K
4 x2 - 4 x + 4
3
O +1
2
1
„x = Å
3
1
H2 x - 1L2 + 3
„ x.
j'@xD „ x = ArcTan@j@xDD + C , scriviamo:
„x = ‡
1
1
2 x-1
1
j@xD2 +1
„x = ‡
3
2
1
H2 x - 1L2 + 3
·
K
„x =
1
2 x-1
3
O +1
2
2
1
„x =
3
2
ArcTanB
3
2x-1
F + C.
3
Esercizio 12.4.1
Calcolare i seguenti integrali:
‡
‡
ü Integrali del tipo ‡
q+ p x
a x2 +b x+c
1
2+x
2
1
7+4x+x
„ x; ‡
2
„ x; ‡
1
29 + 10 x + x
2
1
2 + 9 x2
„ x; ‡
„ x;
1
10 + 12 x + 4 x2
„ x.
‚ x, con D < 0.
Per il calcolo di integrali di questo tipo, si ricorre al trucco di far apparire, al numeratore, la derivata del denominatore, cioé
2 a x + b; l'integrale si decompone allora nella somma di un integrale immediato, che ha per risultato un logaritmo, e di un
integrale del tipo precedente.
Esempio 12.4.5
Calcolare l'integrale:
‡
2x-3
2 x2 + 1
„ x.
La derivata del denominatore è 4 x, quindi conviene scrivere:
‡
Il primo integrale è del tipo ‡
1
j@xD
4x
1
1
„x = Å ‡
„x - 3‡
„ x.
2
2 x2 + 1
2 x2 + 1
2 x2 + 1
2x-3
j'@xD „ x = Log@ » j@xD »D + C , e il secondo è del tipo precedente, e si riconduce
facilmente ad un arcotangente. In definitiva:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
‡
291
12. Integrali indefiniti
ArcTanB 2 xF
4x
1
1
1
+ C.
„x = Å ‡
„x - 3‡
„ x = Å LogA2 x2 + 1E - 3
2
2
2 x2 + 1
2 x2 + 1
2 x2 + 1
2
2x-3
Esempio 12.4.6
Calcolare l'integrale:
‡
4x+3
3x -4x+2
2
„ x.
La derivata del denominatore è 6 x - 4, quindi questa volta conviene scrivere:
‡
4x+3
„x =
3x -4x+2
2
Å4 H4 x + 3L
6 x + Å2
6 x - 4 + 4 + Å2
6x-4+ 2
4
4
4
4
„x = Å ·
„x = Å ·
„x = Å ·
„ x.
Å ·
6
6
6
6
3 x2 - 4 x + 2
3 x2 - 4 x + 2
3 x2 - 4 x + 2
3 x2 - 4 x + 2
6
9
9
17
A questo punto decomponiamo l'ultimo integrale nella somma di un integrale immediato e di uno del tipo precedente:
6x-4+ 2
6x-4
1
4
4
4 17
„x = Å ·
„x = Å ‡
„x + Å
„x =
‡
‡
6
6 3 x2 - 4 x + 2
6 2
3 x2 - 4 x + 2
3 x2 - 4 x + 2
3 x2 - 4 x + 2
17
4x+3
17
4
= Å LogA3 x2 - 4 x + 2E +
3
6
ArcTanB
-2+3 x
2
F
2
2
17
-2 + 3 x
+ C = Å LogA3 x2 - 4 x + 2E +
ArcTanB
F + C.
3
2
3 2
Esercizio 12.4.2
Calcolare i seguenti integrali:
‡
x+5
7+4x+x
2
‡
ü Integrali del tipo ‡
p x+q
a x2 +b x+c
„ x; ‡
x+1
29 + 10 x + x2
2-3x
2+9x
2
„ x; ‡
„ x; ‡
x
2 + x2
4x-3
10 + 12 x + 4 x2
„ x;
„ x.
‚ x, con D > 0.
In questo caso il denominatore può essere scritto come prodotto della costante a e di due fattori di primo grado:
a x2 + b x + c = a Hx - x1 L Hx - x2 L, dove x1 e x2 sono le due radici reali e distinte dell'equazione a x2 + b x + c = 0. La
frazione
p x+q
a x2 +b x+c
ammette allora una decomposizione in fratti semplici del tipo:
px+q
a x2 + b x + c
=
a Hx - x1 L
A
+
B
x - x2
,
dove le due costanti A e B possono essere calcolate col principio di identità dei polinomi. I due integrali ‡
‡
1
x-x2
„ x possono poi essere calcolati immediatamente, e danno luogo a due logaritmi.
Esempio 12.4.7
Calcolare l'integrale:
‡
3x+1
x2 - x - 6
„ x.
Le radici del denominatore sono x1 = -2 e x2 = 3. Cerchiamo una decomposizione del tipo:
Settembre 2008
1
x-x1
„x e
Carlo Greco
Appunti di Analisi Matematica I
292
12. Integrali indefiniti
3x+1
x2 - x - 6
=
A
x+2
+
B
x-3
a tale scopo, riduciamo il secondo membro allo stesso denominatore:
A
x+2
+
B
=
x-3
A Hx - 3L + B Hx + 2L
Hx + 2L Hx - 3L
Ora, affinché si abbia:
3x+1
x2 - x - 6
;
HA + BL x - 3 A + 2 B
=
x2 - x - 6
.
HA + BL x - 3 A + 2 B
=
x2 - x - 6
dev'essere, evidentemente:
:
A+B=3
-3 A + 2 B = 1
Questo sistema si risolve immediatamente, e si ottiene A = 1 e B = 2, vale a dire che si ha:
3x+1
x2 - x - 6
=
1
x+2
+
2
x-3
.
Ma allora:
‡
3x+1
x2 - x - 6
„x = ‡
1
x+2
+
„x = ‡
2
x-3
1
x+2
„x +‡
2
x-3
„ x = Log@ » x + 2 »D + 2 Log@ » x - 3 »D + C.
Esempio 12.4.8
Calcolare l'integrale:
‡
x
2x -3x-2
2
„ x.
1
2
Le radici del denominatore sono x1 = - Å e x2 = 2. Cerchiamo una decomposizione del tipo:
x
=
2 x2 - 3 x - 2
riduciamo il secondo membro allo stesso denominatore:
A
2 Ix + Å2 M
1
+
B
x-2
=
A
2x+1
+
B
x-2
2x -3x-2
1
B
x-2
;
H2 x + 1L Hx - 2L
Ora, affinché si abbia:
x
2 Ix + Å2 M
+
A Hx - 2L + B H2 x + 1L
=
2
A
=
=
HA + 2 BL x - 2 A + B
2 x2 - 3 x - 2
HA + 2 BL x - 2 A + B
2 x2 - 3 x - 2
dev'essere:
:
A+2B = 1
-2 A + B = 0
da cui: A = Å1 e B = Å2 , vale a dire che si ha:
5
5
x
2x -3x-2
2
Ma allora:
Settembre 2008
1
=
2
Å5
2 Ix + M
1
Å2
+
Å5
x-2
=
1
1
10 x +
1
Å2
2 1
.
+Å
5 x-2
.
Carlo Greco
Appunti di Analisi Matematica I
‡
·
1
1
1
Å2
10 x +
293
12. Integrali indefiniti
x
2x -3x-2
2
„x =
1
1
2
1
2 1
2
1
2
„x =
LogB x + Å F + Å Log@ » x - 2 »D + C.
+Å
„x =
„x + Å ‡
·
1
10
x-2
10
5 x-2
5
2
5
x + Å2
Esercizio 12.4.3
Calcolare i seguenti integrali:
‡
3-x
3 x2 + 2 x - 1
‡
ü Integrali del tipo ‡
q+ p x
a x2 +b x+c
3x
6-5x+x
2
„ x; ‡
1+x
x2 - 3 x
„ x; ‡
5x-2
‡
„ x;
‡
„ x;
x - 25
2
1
„ x;
x2 - x - 2
3-2x
x -x-2
2
„ x.
‚ x, con D = 0.
In questo caso l'equazione a x2 + b x + c = 0 ammette due radici reali coincidenti x1 = x2 ª x0 = -
pertanto il quadrato di un binomio: a x + b x + c = a Hx - x0 L , quindi:
2
b
2a
; il denominatore è
2
px+q
ax +bx+c
2
=
px+q
a Hx - x0 L2
.
Si cerca allora una decomposizione del tipo:
px+q
a x2 + b x + c
=
a Hx - x0 L
A
B
Hx - x0 L2
+
.
Esempio 12.4.9
Calcolare l'integrale:
‡
5x-2
Hx + 4L2
„ x.
Cerchiamo una decomposizione della forma:
5x-2
Hx + 4L2
Si ha:
A
x+4
+
B
Hx + 4L
2
=
=
A
x+4
+
B
Hx + 4L2
A Hx + 4L + B
Hx + 4L
=
2
.
Ax+4A+B
Hx + 4L2
,
pertanto dev'essere:
:
A=5
4 A + B = -2
da cui: A = 5, B = -22, cioé si ha:
5x-2
Hx + 4L2
=
5
x+4
-
22
Hx + 4L2
.
Pertanto:
‡
Settembre 2008
5x-2
Hx + 4L
2
„x = ‡
5
x+4
-
22
Hx + 4L
2
„x = ‡
5
x+4
„x -‡
22
Hx + 4L
2
„ x = 5 Log@ » x + 4 »D +
22
x+4
+ C.
Carlo Greco
Appunti di Analisi Matematica I
294
12. Integrali indefiniti
Esempio 12.4.10
Calcolare l'integrale:
‡
3x
„ x.
4 x - 12 x + 9
2
Il denominatore è, anche in questo caso, un quadrato perfetto: 4 x2 - 12 x + 9 = H2 x - 3L2 = 4 Ix - Å M . Cerchiamo allora
3 2
2
una decomposizione della forma:
3x
4 x - 12 x + 9
2
Si ha:
A
4 Ix - Å2 M
3
+
A
4 Ix - M
=
3
Å2
+
A Ix - Å2 M + 4 B
B
Ix - Å2 M
3 2
3
B
Ix - Å2 M
4 Ix - Å2 M
=
3 2
2
3
.
3
=
A x - Å2 A + 4 B
4 x2 - 12 x + 9
,
pertanto dev'essere:
:
A=3
3
- Å2
A+4B = 0
9
da cui: A = 3, B = Å , cioé si ha:
8
3x
4 x2 - 12 x + 9
=
9
3
4 Ix - Å2 M
3
+
Å8
Ix - Å2 M
3 2
.
Pertanto:
‡
3x
4 x2 - 12 x + 9
„x = ·
1
1
3
9
„x = Å ·
„x + Å ·
„x =
3
4
8
3 2
x - Å2
Ix - Å2 M
9
3
4 Ix - Å2 M
+
3
Å8
Ix - Å2 M
3 2
1
3
3
9 -1
3
3
9
+ C.
= Å LogB x - Å F + Å
+ C = Å LogB x - Å F - Å
4
2
8 x - Å3
4
2
4 2x-3
2
Esercizio 12.4.4
Calcolare i seguenti integrali:
‡
2-3x
9 + 12 x + 4 x2
‡
‡
ü Integrali del tipo ‡
P@xD
a x2 +b x +c
x+1
H2 + xL2
‡
„ x;
‡
„ x;
3
4 - 12 x + 9 x
2
-5 x
1 + 4 x + 4 x2
1-5x
16 + 8 x + x2
„ x;
‡
x
„ x;
„ x;
H1 - xL2
„ x.
‚ x, con P@xD polinomio di grado maggiore o uguale a due
In questo caso ci si riconduce ai casi precedenti semplicemente effettuando la divisione dei polinomi.
Esempio 12.4.11
Calcolare l'integrale:
‡
Settembre 2008
2 x3 - x + 1
2 x2 + 1
„ x.
Carlo Greco
Appunti di Analisi Matematica I
295
12. Integrali indefiniti
Eseguendo la divisione indicata, si ha immediatamente:
2 x3 - x + 1
2x +1
2
=x+
1-2x
2 x2 + 1
,
da cui:
‡
‡ x+
1-2x
2 x2 + 1
„x = ‡ x „x +‡
1-2x
2 x2 + 1
„x =
2 x3 - x + 1
2 x2 + 1
+‡
x2
2
„x =
1-2x
2 x2 + 1
„x =
x2
2
ArcTanB 2 xF
+
2
Esercizio 12.4.5
Calcolare i seguenti integrali:
‡
‡
‡
x4 - 3 x + 2
7 + 4 x + x2
x2 + x
29 + 10 x + x2
1 - x2
16 + 8 x + x2
„ x; ‡
„ x; ‡
„ x;
‡
x2 + 2 x
2 + 9 x2
„ x;
x3 - 1
5 + 6 x + 2 x2
x4 + 1
4 - 12 x + 9 x2
„ x;
„ x.
ü Esercizi
Esercizio 12.4.6
Calcolare i seguenti integrali indefiniti di funzioni razionali fratte.
Nuova tavola Reset
Esercizio 12.4.7
Calcolare i seguenti integrali indefiniti di funzioni razionali fratte.
Numeratore:
Tipo:
Pn = 1 Pn = 1 Pn ¥ 2
D > 0 D = 0 D < 0 Casuale
Nuova funzione Soluzione Reset
5. Integrali particolari
In questa sezione vogliamo calcolare alcuni integrali che possono presentarsi nelle applicazioni.
Esempio 12.5.1
Calcolare l'integrale:
Ÿ
1
Sin@xD
„ x.
In questo caso conviene applicare la formula: Sin@2 aD = 2 Sin@aD Cos@aD; nel nostro caso:
Settembre 2008
1
- Å LogA1 + 2 x2 E + C.
2
Carlo Greco
Appunti di Analisi Matematica I
296
12. Integrali indefiniti
Sin@xD = 2 SinA Å E CosA Å E,
x
x
2
2
quindi:
Ÿ
=·
„x = ‡
1
Sin@xD
2 SinB Å F CosB Å F
1
x
2
„ x =‡
1
1
1
Å
x
TanB Å F CosB Åx F2 2
2
x
2
Ÿ
1
2 TanB Å F CosB Å F
x
2
x 2
2
„x =
DATanA Å EE „ x = Log[|TanA Å E|]+C
TanB Å F
x
2
1
x
2
2
In definitiva:
„x = ·
x
2
„ x = Log[|TanA Å E|]+C.
x
1
Sin@xD
2
Più in generale, applicando esattamente lo stesso metodo dell'esempio precedente, si verifica che:
Ÿ
1
Sin@x+aD
„ x = Log[|TanA
x+a
2
E|]+C.
Esempio 12.5.2
Calcolare l'integrale:
Ÿ
1
Cos@xD
„ x.
In questo caso conviene osservare che Cos@xD = SinAx + Å E, e applicare la formula precedente. Dunque:
p
2
Ÿ
1
Cos@xD
„x =‡
SinBx+ Å F
1
p
2
„ x = Log[|TanB
F|]+C = Log[|TanA Å + Å E|]+C.
p
2
x+ Å
2
x
p
2
4
Esempio 12.5.3
Calcolare l'integrale:
Ÿ
Utilizziamo le formule di bisezione: Cos@aD2 =
Ÿ
1
1+Cos@xD
1+Cos@2 aD
„ x.
, pertanto 1 + Cos@aD = 2 CosA Å E , quindi:
a 2
2
2
„x =·
1
1+Cos@xD
1
2 CosB Å F
x 2
2
„ x = Ÿ DATanA Å EE „ x = TanA Å E+C.
x
2
x
2
Esempio 12.5.4
Calcolare l'integrale:
Ÿ
1
1+Sin@xD
„ x.
In questo caso conviene moltiplicare numeratore e denominatore per 1 - Sin@xD; si ottiene:
1
1+Sin@xD
=
1-Sin@xD
1-Sin@xD2
=
1-Sin@xD
Cos@xD2
=
1
Cos@xD2
-
1
Cos@xD2
Sin[x];
l'integrale dato diventa quindi la differenza di un integrale immediato ed uno immediato generalizzato:
Ÿ
1
1+Sin@xD
‡
„x =‡
1
Cos@xD2
1
„x +‡
1
Cos@xD2
= Tan[x] -
Settembre 2008
-
Cos@xD2
1
Cos@xD2
Sin@xD „ x =
D@Cos@xDD „ x =
1
Cos@xD
+C.
Carlo Greco
Appunti di Analisi Matematica I
297
12. Integrali indefiniti
Esempio 12.5.5
Calcolare gli integrali:
2
2
Ÿ Sin@xD „ x, Ÿ Cos@xD „ x.
Per calcolare questi integrali conviene usare la formule di bisezione:
Analogamente:
Ÿ Sin@xD2 „ x = Ÿ
1-Cos@2 xD
Ÿ Cos@xD2 „ x = Ÿ
1+Cos@2 xD
2
2
„ x = Ÿ Å „ x - Å Ÿ 2 Cos@2 xD „ x = Å x - Å Sen@2 xD + C .
2
4
2
4
1
1
1
1
„ x = Ÿ Å „ x + Å Ÿ 2 Cos@2 xD „ x = Å x + Å Sen@2 xD + C .
2
4
2
4
1
1
1
1
Le formule di bisezione possono essere usate per calcolare integrali del tipo
Ÿ Sin@xDn „ x, Ÿ Cos@xDn „ x,
con n pari.
Esempio 12.5.6
Calcolare l'integrale Ÿ Sin@xD4 „ x:
Ÿ Sin@xD4 „ x = Ÿ I
2
=
Per calcolare integrali del tipo
M „ x = Ÿ I Å Cos@2 xD2 - Å Cos@2 xD + Å M „ x
1-Cos@2 xD 2
3x
8
1
4
1
4
- Å Sin@2 xD +
1
2
1
32
1
4
Sin@4 xD + C.
Ÿ Sin@xDn „ x, Ÿ Cos@xDn „ x,
con n dispari, si può procedere come segue.
Esempio 12.5.7
Calcolare l'integrale Ÿ Sin@xD3 „ x.
Si ha:
Ÿ Sin@xD3 „ x = Ÿ Sin@xD2 Sin@xD „ x = Ÿ I1 - Cos@xD2 M Sin@xD „ x =
= Ÿ Sin@xD „ x + Ÿ Cos@xD2 H-Sin@xDL „ x =
1
= -Cos@xD + Å Cos@xD3 + C .
3
In definitiva, con i metodi illustrati, è possibile calcolare gli integrali del tipo Ÿ Sin@xDn „ x, Ÿ Cos@xDn „ x con n qualsiasi.
Funzione:
Sin Cos
n
‡ sinHxL „ x = -cosHxL
Vediamo ora come calcolare gli integrali del tipo Ÿ Sin@xD p Cos@xDq „ x; consideriamo anzitutto il caso in cui uno dei due
esponenti p, q, è dispari.
Esempio 12.5.8
Calcolare l'integrale:
Settembre 2008
Ÿ Sin@xD5 Cos@xD4 „ x.
Carlo Greco
Appunti di Analisi Matematica I
298
12. Integrali indefiniti
Possiamo scrivere:
5
4
4
4
2
4
Ÿ Sin@xD Cos@xD „ x = Ÿ Sin@xD Sin@xD Cos@xD „ x = =Ÿ I1 - Cos@xD M Sin@xD Cos@xD „ x =
2
=Ÿ I1 - Cos@xD2 M Cos@xD4 Sin@xD „ x =
2
= Ÿ ICos@xD8 - 2 Cos@xD6 + Cos@xD4 M Sin@xD „ x.
A questo punto siamo ricondotti a integrali del tipo Ÿ Cos@xDn Sin@xD „ x, che sono integrali indefiniti immediati
generalizzati, e si calcolano immediatamente. Dunque:
-Ÿ ICos@xD8 - 2 Cos@xD6 + Cos@xD4 M D@Cos@xDD „ x =
1
1
1
= - Å Cos@xD9 - 2 Å Cos@xD7 + Å Cos@xD5 + C.
9
7
5
Nel caso in cui entrambe gli esponenti p e q sono pari, ci si riconduce facilmente ad un integrale del tipo Ÿ Sin@xDn „ x o
Ÿ Cos@xDn „ x, che abbiamo visto prima.
Esempio 12.5.9
Calcolare l'integrale: Ÿ Sin@xD4 Cos@xD2 „ x;
Possiamo scrivere:
Ÿ Sin@xD4 Cos@xD2 „ x = Ÿ Sin@xD4 I1 - Sin@xD2 M „ x =
= Ÿ ISin@xD4 - Sin@xD6 M „ x =
=
3x
1
5 x 15
3
1
1
- Å Sin@2 xD +
Sin@4 xD Sin@2 xD +
Sin@4 xD Sin@6 xD + C =
8
32
16 64
64
192
4
=
x
16
-
1
64
Sin@2 xD -
1
64
Sin@4 xD +
1
192
Sin@6 xD
Possiamo così, in linea di principio, calcolare tutti gli integrali del tipo Ÿ Sin@xD p Cos@xDq „ x.
p
q
1
2
‡ cosHxL sinHxL „ x = - Å cos HxL
2
Supponiamo di voler calcolare l'integrale indefinito di una certa funzione f @xD:
6. Integrazione per sostituzione
‡ f @xD „ x.
Può essere conveniente, talvolta, considerare invece dell'integrale dato, il seguente integrale indefinito:
‡ f @j@tDD j'@tD „ t;
esso si ottiene da quello dato esprimendo la variabile indipendente x come funzione di un parametro t: x = j@tD, e
sostituendo all'espressione „ x, l'espressione j '@tD „ t.
Il nuovo integrale, nella variabile t, può essere, con una opportuna scelta della funzione j@tD, più facile da calcolare rispetto
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
299
12. Integrali indefiniti
a quello dato. In tal caso, il risultato sarà una funzione della variabile t, che chiamiamo G@tD:
‡ f @j@tDD j '@tD „ t = G@tD + C.
E' facile verificare che, indicata con F@xD una primitiva di f @xD, le due funzioni F@j@tDD e G@tD sono entrambe primitive
della stessa funzione, infatti, applicando la formula di derivazione delle funzioni composte, si ha:
(F[j[t]])' = F'[j[t]] j'[t] = f[j[t]] j'[t] = G'[t].
Da ciò consegue che le due funzioni F@j@tDD e G@tD differiscono per una costante nell'intervallo in cui varia t, cioé:
F[j[t]] = G[t] + C.
Supponiamo ora che sia possibile esprimere viceversa t in funzione di x, invertendo la funzione x = j@tD: t = y@xD; si ha
allora:
F[x] = G[y[x]] + C.
Quanto esposto sopra può essere riassunto nella formula:
‡ f @xD „ x = K‡ f @j@tDD j'@tD „ tO
t=y@xD
che si dice formula di integrazione per sostituzione.
Esempio 12.6.1
Calcolare l'integrale:
‡
1
1 + ‰x
„ x.
Poniamo x = Log@tD (quindi nel nostro caso j@tD = Log@tD), nonché „ x = j'@tD „ t; essendo ‰Log@tD = t, otteniamo così il
nuovo integrale:
‡
1
1
Å „t = ‡
„ t.
1+t t
t H1 + tL
1
Quest'ultimo integrale, nella variabile t, si calcola facilmente:
‡
t H1 + tL
1
„t = ‡
1
1
Å „ t = Log@ » t »D - Log@ » 1 + t »D + C.
t 1+t
Ora, essendo x = Log@tD, si ha t = ‰x , e, sostituendo nella primitiva Log@ » t »D - Log@ » 1 + t »D + C trovata, si ha:
Log@ » t »D - Log@ » 1 + t »D + C = Log@ » ‰x »D - Log@ » 1 + ‰x »D + C.
Eliminando i valori assoluti (cosa lecita in questo caso) e ricordando le proprietà dei logaritmi, si ha:
Log@ » ‰x »D - Log@ » 1 + ‰x »D + C = x - Log@1 + ‰x D + C.
Osservazione. Gli integrali indefiniti immediati generalizzati sono un tipo di integrali che si potrebbero calcolare per
sostituzione, se non ne conoscessimo già il risultato. Ad esempio, l'integrale:
‡
Log@xD
x
„x
è un integrale indefinito immediato generalizzato, infatti possiamo scrivere:
‡
Log@xD
x
Log@xD2
1
+ C.
„ x = ‡ Log@xD Å „ x = ‡ Log@xD D@Log@xDD „ x =
2
x
Possiamo però calcolarlo anche, in modo del tutto naturale, per sostituzione, ponendo x = ‰t ; infatti in tal caso si ha:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
300
12. Integrali indefiniti
‡
Log@xD
x
„x = ‡
LogA‰t E
‰t
‰t „ t = ‡ t „ t =
t2
2
+C=
Log@xD2
2
+ C.
Possiamo dire, in effetti che, con gli integrali indefiniti immediati generalizzati, abbiamo anticipato il metodo di
integrazione per sostituzione ad alcuni casi particolari.
Esempio 12.6.2
Calcolare l'integrale:
‡
Poniamo x = t2 , da cui, supponendo t ¥ 0, t =
‡
„x = ‡
1
1+
1+
„ x.
x
x:
1
x=t2
x
1
1+t
2 t „t = 2‡
t
1+t
„t = 2‡ 1 -
2 Ht - Log@ » 1 + t »DL + C = 2 I x - LogA1 +
1
1+t
„t =
x EM + C.
t= x
Esempio 12.6.3
Calcolare l'integrale:
‡
Conviene porre x =
3 - x2 „ x.
p
p
2
2
3 Sin@tD, da cui, supponendo - Å § t § Å :
‡
‡
x= 3 Sin@tD
=
3 Cos@tD „ t = 3 ‡
3 - 3 Sin@tD2
3‡
3 - x2 „ x
1 - Sin@tD2 Cos@tD „ t =
Cos@tD2 Cos@tD „ t = 3 ‡ Ã Cos@tD Ã Cos@tD „ t = 3 ‡ Cos@tD2 „ t.
L'ultimo integrale può essere calcolato, ad esempio, ricorrendo alla formula: Cos@tD2 = Å H1 + Cos@2 tDL:
1
2
3
3
1
3 ‡ Cos@tD2 „ t = Å ‡ H1 + Cos@2 tDL „ t = Å t + Å Sin@2 tD + C.
2
2
2
In definitiva:
‡
3 - x2 „ x
x= 3 Sin@tD
=
3
1
3
Å t + Å Sin@2 tD + C = Å Ht + Sin@ tD Cos@tDL + C
2
2
2
Infine, invertendo la relazione x =
che
3 - x2 =
p
x
2
2
3
3 Cos@xD, si ottiene:
‡
x
x
3
F+
3 - x „ x = Å ArcSinB
2
3
3
2
x
x
3
F+ Å
Å ArcSinB
3
2
3
Settembre 2008
p
3 Sin@tD (cosa possibile se - Å § t § Å ), si ha: t = ArcSinB
3 - x2
3
3 - x2 + C.
+C =
F, ed osservando anche
Carlo Greco
Appunti di Analisi Matematica I
301
12. Integrali indefiniti
Calcolare, col metodo di sostituzione, i seguenti integrali indefiniti:
SinA x E
·
‡
„ x;
x
x
‡ ArcTanA x E „ x.
„ x;
1+
x
7. Esercizi
Esercizio 12.7.1
Calcolare i seguenti integrali.
Ÿ
‡
Log@Sin@xDD
‡
Ÿ
p
p
2
2
Sin@xD + 1 „ x, con - Å < x < Å (porre Sin@xD = t);
1
Sin@xD Cos@xD
·
Cos@xD2
x6 +2 x2 -1
„ x;
3 x2 +1
3
x3 +x+1
x4 -1
‡
„ x; Ÿ Tan@xD2 „ x;
„ x (porre x2 = t);
Sin@2 xD
2+Sin@xD2
„ x; ‡
Ÿ0
„ x; ‡
Log@xD
x
1
x
„ x; ‡
pê4 Tan@xD3 +Tan@xD
Tan@xD2 +4
„ x;
1-Log@xD2
1
1+ x
„ x;
„ x.
Una funzione f @xD si dice integrabile elementarmente se le sue primitive sono esprimibili mediante una combinazione
8. Funzioni non integrabili elementarmente
(somma, prodotto, quoziente, composta) di un numero finito di funzioni elementari.
Le funzioni elementari che conosciamo sono molto poche: polinomi e funzioni razionali fratte, l'esponenziale e il
logaritmo, le funzioni trigonometriche e le loro inverse. E' evidente che esse non possono essere sufficienti ad esprimere le
primitive di tutte le funzioni che si possono incontrare nelle applicazioni.
Ad esempio, la funzione f @xD = ‰-x , di cui rappresentiamo il grafico nella figura seguente:
2
f @xD = ‰-x
y
2
0.8
0.6
0.4
0.2
-2
-1
1
2
x
è una tipica funzione il cui integrale
-x
‡ ‰ „x
2
non può essere calcolato elementarmente, cioé non ammette primitive esprimibili tramite le funzioni elementari che
conosciamo. Ciò non significa che tali primitive non esistano, infatti per il teorema sull'esistenza delle primitive per le
funzioni continue, sappiamo che la funzione:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
302
12. Integrali indefiniti
F@xD = ‡ ‰-x „ x
x
2
0
2
è senz'altro una primitiva di ‰-x , solo che non è una funzione elementare di nostra conoscenza, né è esprimibile tramite
funzioni a noi note.
Allo scopo di ampliare le nostre possibilità di calcolare gli integrali, sono state introdotte varie funzioni speciali, che vanno
ad arricchire lo "zoo" di funzioni note. Una di esse è la cosiddetta funzione degli errori di Gauss, che è definita (a meno di
una costante), proprio come la primitiva di ‰-x , e si indica con Erf @xD:
2
Erf @xD ª
2
p
-x
‡ ‰ „ x;
x
2
0
f @xD = Erf @xD
y
il suo grafico è il seguente:
0.5
-2
-1
1
2
x
-0.5
-1.0
Essa consente non solo di calcolare l'integrale Ÿ ‰-x „ x (in quanto, ovviamente: Ÿ ‰-x „ x =
2
2
p
2
Erf @xD + C , ma anche
molti altri integrali simili. Ad esempio, consideriamo l'integrale:
2 -x
‡ x ‰ „ x;
2
integrando per parti si ha:
x
x -x2
1 -x2
x -x2 1
2 -x2
-x2
-x2
‡ x ‰ „ x = -‡ Å I-2 x ‰ M „ x = - Å ‰ - ‡ Å ‰ „ x = - Å ‰ + Å ‡ ‰ „ x;
2
2
2
2
2
l'ultimo integrale non è calcolabile elementarmente, ma se ricorriamo alla funzione degli errori abbiamo:
p Erf @xD + C.
x -x2 1
x -x2 1
2 -x2
-x2
‡ x ‰ „x = - Å ‰ + Å ‡ ‰ „x = - Å ‰ + Å
2
2
2
4
2
In modo analogo è possibile calcolare molti altri integrali importanti che coinvolgono, in qualche modo, la funzione ‰-x .
La funzione degli errori è solo una delle molte funzioni speciali che sono state introdotte per il calcolo di integrali
importanti per la matematica e le sue applicazioni. Nella seguente tabella elenchiamo, a titolo esemplificativo, alcune di
esse.
Nome
funzione
SinIntegral@xD
FresnelS@xD
FresnelC@xD
Settembre 2008
Definizione
SinIntegral@xD = Ÿ0
x Sin@tD
t
FresnelS@xD
„t
x
p
= Ÿ0 SinA Å2 t2 E „ t
FresnelC@xD = Ÿ0 CosA Å2 t2 E „ t
x
p
Carlo Greco
Appunti di Analisi Matematica I
13. Infinitesimi e Infiniti
303
13 Infinitesimi e Infiniti
1. Generalità sugli infinitesimi
Diamo la seguente definizione.
(Funzione infinitesima)
Definizione 13.1.1
Sia X un intervallo, sia x0 œ X , e sia f : X \ 8x0 < Ø  , una funzione definita in X \ 8x0 <. Se risulta:
lim f @xD = 0
si dice che la funzione f @xD è infinitesima in x0 .
xØ x0
Dunque, una funzione infinitesima in x0 è semplicemente una funzione il cui limite, per x Ø x0 , è uguale a zero.
Naturalmente la funzione f @xD può essere o non essere definita anche nel punto x0 , come mostrano i seguenti esempi.
Esempio 13.1.1
Le seguenti funzioni sono continue e si annullano nel punto x0 , quindi sono infinitesime:
- la funzione Log@xD è infinitesima in x0 = 1;
- la funzione Sin@xD è infinitesima in x0 = k p per ogni k œ .
Esempio 13.1.2
Le seguenti funzioni non sono definite nel punto x0 , ma tendono comunque a zero per x Ø x0 , e quindi sono infinitesime:
-
- la funzione ‰
- la funzione
1
x2
1
Tan@xD
è infinitesima in x0 = 0;
p
è infinitesima in x0 = Å .
2
Esempio 13.1.3
La seguente funzione è definita nel punto x0 , non si annulla per x = x0 , ma tende a zero per x Ø x0 , e quindi è infinitesima:
f @xD =
-1íx2
‰
0
se x ∫ 0
se x = 0
La definizione precedente riguarda il caso in cui x0 è un numero reale. Nel caso in cui x0 = +¶ o x0 = -¶, la definizione
di funzione infinitesima si modifica leggermente come segue.
(Funzione infinitesima)
Definizione 13.1.2
Sia X un intervallo illimitato superiormente (risp. inferiormente) e sia f : X Ø  una funzione definita in X . Se risulta:
lim f @xD = 0 (risp. lim f @xD = 0),
si dice che la funzione f @xD è infinitesima per x Ø +¶ (risp. per x Ø -¶ ).
xØ+¶
xØ-¶
Il motivo principale per cui si introduce il concetto di funzione infinitesima, consiste nella possibilità di effettuare una
specie di confronto tra due funzioni entrambe infinitesime nello stesso punto x0 .
Per tale motivo è fondamentale la seguente definizione.
Definizione 13.1.3
(Confronto tra infinitesimi)
Siano f @xD e g@xD due funzioni infinitesime in x0 .
1°) Se risulta:
lim
f @xD
=0
si dice che la funzione f @xD è infinitesima per x Ø x0 , di ordine superiore rispetto a g@xD.
xØ x0 g@xD
2°) Se risulta:
lim À
f @xD
À = +¶ ,
si dice che la funzione f @xD è infinitesima per x Ø x0 , di ordine inferiore rispetto a g@xD.
xØ x0
3°) Se risulta:
g@xD
lim À
f @xD
À= b,
dove b è un numero reale diverso da zero, si dice che la funzione f @xD è infinitesima per x Ø x0 , dello stesso ordine di g@xD.
xØ x0
Settembre 2008
g@xD
Carlo Greco
Appunti di Analisi Matematica I
304
13. Infinitesimi e Infiniti
Diamo i seguenti esempi.
Esempio 13.1.4
Le funzioni Sin@xD ed x sono infinitesime dello stesso ordine per x Ø 0, infatti:
lim
Sin@xD
= 1,
x
xØ0
quindi siamo nel 3°) caso della definizione.
Esempio 13.1.5
Le funzioni Log@x + 1D ed x sono infinitesime dello stesso ordine per x Ø 0, infatti:
Log@x + 1D
lim
= 1,
x
xØ0
quindi siamo nel 3°) caso della definizione.
Esempio 13.1.6
La funzione 1 - Cos@xD è infinitesima di ordine superiore rispetto a Sin@xD per x Ø 0, infatti:
lim
1 - Cos@xD
Sin@xD
xØ0
= lim
1 - Cos@xD
x
x2
Sin@xD
xØ0
x = 0,
quindi siamo nel 1°) caso della definizione.
Esempio 13.1.7
La funzione Tan@xD2 è infinitesima di ordine inferiore rispetto a x3 per x Ø 0, infatti:
Tan@xD2
lim
x3
xØ0
Tan@xD2 1
Å
x
x2
= lim
xØ0
= +¶,
quindi siamo nel 2°) caso della definizione. Notiamo esplicitamente il ruolo del valore assoluto nella definizione
precedente: se non ci fosse stato, in questo caso avremmo avuto che il limite limxØ0
Tan@xD2
x3
non esiste, infatti, come si vede
immediatamente:
lim-
Tan@xD2
x3
xØ0
= -¶,
lim+
Tan@xD2
x3
xØ0
= +¶.
I precedenti esempi riguardavano il confronto tra funzioni infinitesime per x Ø x0 , dove x0 œ . Diamo ora alcuni esempi
in cui si confrontano funzioni infinitesime per x Ø +¶ o per x Ø -¶.
Esempio 13.1.8
Le funzioni 2 ArcTan@xD - p ed Å1 sono infinitesime dello stesso ordine per x Ø +¶, infatti:
x
lim
2 ArcTan@xD - p
1
xØ+¶
2
1+x2
H
= lim
xØ+¶
Åx
-
1
= - lim
xØ+¶
2
2 x2
1 + x2
= -2
x
quindi siamo nel 1°) caso della definizione.
Esempio 13.1.9
La funzione ‰x è infinitesima di ordine superiore rispetto a
lim
‰x
xØ-¶ 1
x2
x=-y
=
lim
yØ+¶
‰-y
1
1
x2
per x Ø -¶, infatti:
= lim
yØ+¶
y2
‰y
H
= lim
yØ+¶
2y
‰y
H
= lim
yØ+¶
y2
quindi siamo nel 2°) caso della definizione.
Esempio 13.1.10
La funzione
Settembre 2008
1
Log@xD
1
x
è infinitesima di ordine inferiore rispetto a Å per x Ø +¶, infatti:
2
‰y
=0
Carlo Greco
Appunti di Analisi Matematica I
305
13. Infinitesimi e Infiniti
lim
xØ+¶
1
Log@xD
1
Åx
= lim
H*L
x
xØ+¶
Log@xD
= lim
xØ+¶
x
Log@xD
H
= lim
1
xØ+¶ 1
Åx
= +¶
(nel passaggio indicato con (*) si può togliere il valore assoluto in quanto, in questo caso, per x > 1 la funzione
x
Log@xD
è
positiva). Siamo dunque nel 3°) caso della definizione.
Terminiamo questo paragrafo introducendo un'utile notazione. Se f @xD è una funzione infinitesima di ordine superiore
rispetto alla funzione g@xD per x Ø x0 , si scrive:
f @xD = o@g@xDD
per x Ø x0 ,
e si legge: f @xD è un "o piccolo" di g@xD per x Ø x0 . Dunque, se f @xD = o@g@xDD per x Ø x0 , ciò significa, semplicemente, che:
lim
xØx0
f @xD
g@xD
= 0,
in accordo con la definizione precedente.
Tra le varie funzioni infinitesime in un punto x0 œ , le più elementari sono quelle del tipo ga @xD = » x - x0 »a , dove
2. Infinitesimi campione e ordine di infinitesimo
a œ + ; notiamo esplicitamente che, grazie al valore assoluto, queste funzioni sono definite in tutto , per qualsiasi valore
di a > 0. Nel seguente grafico si vede l'andamento di queste funzioni per diversi valori di a.
||| a = 1
~a>1
~a<1
y
a=1.6
a=1.4
a=1.2
a=1.
a=0.8
a=0.6
a=0.4
a=0.2
x
x0
Come si vede, la funzione ga @xD ha un andamento "tipo" radice per 0 < a < 1, con un punto cuspidale in x0 ; per a = 1
coincide con la funzione » x - x0 », e infine, per a > 1, ga @xD ha un andamento "tipo" parabola.
Se invece consideriamo il caso in cui x0 = +¶, oppure x0 = -¶, osserviamo che le più elementari funzioni infinitesime
per x Ø ≤¶ sono le funzioni del tipo ga @xD =
1
,
» x »a
||| a = 1
~a<1
~a>1
y
3
2
1
1
Settembre 2008
2
3
4
5
x
dove a œ + , che hanno un andamento "tipo" iperbole.
Carlo Greco
Appunti di Analisi Matematica I
306
13. Infinitesimi e Infiniti
Tali funzioni ga @xD si dicono infinitesimi campione per x Ø x0 , ed ha senso confrontare altre funzioni infinitesime in x0
con tali infinitesimi campione. A tale scopo, si da la seguente definizione.
(Ordine di infinitesimo 1)
Definizione 13.2.1
Sia f @xD una funzione infinitesima in x0 , e sia a œ + ; la funzione f @xD si dice infinitesima di ordine superiore, (risp. di
ordine inferiore) ad a se essa risulta infinitesima di ordine superiore (risp. di ordine inferiore) alla funzione ga @xD.
La funzione f @xD si dice infinitesima di ordine a se essa risulta infinitesima dello stesso ordine di ga @xD.
Esempio 13.2.1
Le funzioni Sin@xD, Tan@xD, ArcSin@xD sono tutte infinitesime di ordine 1 per x Ø 0.
La funzione Log@xD è infinitesima di ordine 1 per x Ø 1.
La funzione
1
x +1
è infinitesima di ordine Å1 per x Ø +¶.
2
La funzione 1 - Cos@xD è infinitesima di ordine 2 per x Ø 0.
Vediamo ora, su degli esempi, come possiamo calcolare l'ordine di infinitesimo di una data funzione per x Ø x0 .
Calcolare l'ordine di infinitesimo della funzione f @xD = ArcCos@xD per x Ø 1.
Esempio 13.2.2
Intanto osserviamo che la funzione data è effettivamente infinitesima per x Ø 1, infatti
lim ArcCos@xD = ArcCos@1D = 0.
xØ1
Ora, l'infinitesimo campione nel punto x0 = 1, è ga @xD = » x - 1 »a ; dobbiamo dunque trovare un a > 0 tale che il limite:
lim
» x - 1 »a
ArcCos@xD
xØ1
esista finito e diverso da zero. A tale scopo, per semplificare i calcoli e liberarci del valore assoluto, osserviamo anzitutto
che tale limite coincide con:
ArcCos@xD
H1 - xLa
lim-
xØ1
,
dato che la funzione ArcCos@xD è definita nell'intervallo @-1, 1D.
Ora, si ha:
1
lim-
ArcCos@xD
xØ1
=
1
a
lim-
xØ1
H1 - xL
a
H
= limxØ1
1
H1 - xLa-1
1-x2
-a H1 - xL
1
1
=
1-x
=
a-1
a
1+x
1
1
a
a-1
1
1
H1 - xL
lim-
xØ1
1
H1 - xL
lim
xØ1-
1
1+x
a- Å
2
=
1-x
2
1
=
a
2
lim-
xØ1
H1 - xL
Ora, fissiamo l'attenzione sull'ultimo limite ottenuto, il cui valore dipende, evidentemente, da a.
Si ha immediatamente:
lim
xØ1-
Pertanto, il limite limxØ1-
H1-xLa
ArcCos@xD
H1 - xL
=
1
a- Å
+¶
0
2
se a > 1 ê 2
se 0 < a < 1 ê 2
è finito e diverso da zero se e solo se a = Å1 ; in tal caso, infatti, si ha:
2
lim
xØ1-
Settembre 2008
se a = 1 ê 2
1
1
ArcCos@xD
H1 - xL
1ê2
1
=
a
=
2
2;
1
1
a- Å
2
.
Carlo Greco
Appunti di Analisi Matematica I
307
13. Infinitesimi e Infiniti
negli altri casi, cioé per a > Å1 , oppure per 0 < a < Å1 , si ha +¶, oppure 0. Dunque, la funzione ArcCos@xD è infinitesima di
2
2
1
ordine Å per x Ø 1.
2
Calcolare l'ordine di infinitesimo della funzione f @xD = 2 ArcTanAx3 E - p per x Ø +¶.
Esempio 13.2.3
Osserviamo che anche in questo caso, la funzione data è effettivamente infinitesima per x Ø +¶, infatti:
p
lim I2 ArcTanAx3 E - pM = 2 Å - p = 0.
xØ+¶
2
Questa volta dobbiamo considerare l'infinitesimo campione per x Ø +¶, che è ga @xD = x-a (non è necessario il valore
assoluto dato che x Ø +¶); dobbiamo dunque trovare un a > 0 tale che il limite:
lim
2 ArcTanAx3 E - p
1
xa
xØ+¶
esista finito e diverso da zero. Si ha:
lim
2 ArcTanAx3 E - p
1
xa
xØ+¶
1
1+x6
H
= 2 lim
xØ+¶
3 x2
-a x-1-a
=-
6
a
lim
xØ+¶
x2
1
x-1-a 1 + x6
=-
6
a
lim
xa+3
xØ+¶
1 + x6
.
E' ovvio, a questo punto, che, affinché l'ultimo limite esista finito e diverso da zero, dev'essere: a + 3 = 6, cioé a = 3.
Dunque, la funzione data è infinitesima di ordine 3 per x Ø +¶.
Consideriamo ora la funzione f @xD = ‰x , che è infinitesima per x Ø -¶; è facile convincersi che essa è infinitesima di
ordine superiore ad a, per qualsiasi a > 0. Infatti, calcoliamo il limite:
lim
xØ-¶
‰x
1
»x»a
= lim
‰x
xØ-¶
y=-x
=
1
H-xLa
lim
yØ+¶
‰-y
1
ya
= lim
ya
yØ+¶
‰y
= lim
yØ+¶
y
‰yêa
a
a
H
= lim
yØ+¶
1
1
‰yêa Åa
= 0.
In tal caso si dice che la funzione f @xD = ‰x è infinitesima di ordine infinitamente grande per x Ø -¶; si da infatti la
seguente definizione.
(Ordine di infinitesimo 2)
Definizione 13.2.2
Sia f @xD una funzione infinitesima per x Ø x0 . Se per ogni a > 0 essa è infinitesima di ordine superiore ad a , si dice che
f @xD è infinitesima di ordine infinitamente grande per x Ø x0 ; analogamente, se per ogni a > 0 essa è infinitesima di
ordine inferiore ad a , si dice che f @xD è infinitesima di ordine infinitamente piccolo per x Ø x0 .
Esempio 13.2.4
La funzione f @xD =
1
Log@xD
è infinitesima per x Ø 0; facciamo vedere che essa è infinitesima di ordine infinitamente piccolo;
a tale scopo, fissiamo un a > 0, e consideriamo il limite:
lim
xØ0
1
Log@xD
a
x
= lim
xØ0
x-a
Log@xD
H
= lim
xØ0
è chiaro che, per qualsiasi valore di a > 0, si ha sempre limxØ0
1
xa
-a x-a-1
1
Åx
= -a lim
xØ0
1
xa
;
= +¶, pertanto per ogni a > 0, la funzione f @xD =
è infinitesima di ordine inferiore ad a, dunque, secondo la definizione precedente, f @xD =
infinitamente piccolo per x Ø 0.
Terminiamo questo paragrafo con un'ultima osservazione.
Settembre 2008
1
Log@xD
1
Log@xD
è infinitesima di ordine
Carlo Greco
Appunti di Analisi Matematica I
308
13. Infinitesimi e Infiniti
Osservazione. Se f @xD è una funzione infinitesima per x Ø x0 , ma non di ordine infinitamente grande o infinitamente
piccolo, non è affatto detto che esista un a > 0 tale che f @xD sia infinitesima esattamente di ordine a per x Ø x0 . Ad
esempio, consideriamo la funzione f @xD =
1
;
x Log@xD
essa è chiaramente infinitesima per x Ø +¶; vediamo se è possibile
calcolarne l'ordine; si ha:
1
x Log@xD
lim
1
xa
xØ+¶
xa-1
= lim
xØ+¶
Log@xD
;
ora, se 0 < a < 1, il numeratore tende a zero e il denominatore a +¶, quindi il limite vale zero; se a = 1 il numeratore è
costante a costante valore 1 e il denominatore tende a +¶, quindi il limite vale ancora zero; infine, se a > 1, il limite si
presenta nella forma indeterminata ¶ , pertanto si ha:
¶
1
x Log@xD
lim
xØ+¶
1
xa
= lim
xa-1
xØ+¶
Ha - 1L xa-2
H
= lim
Log@xD
1
Åx
xØ+¶
= Ha - 1L lim xa-1 = +¶.
xØ+¶
In definitiva:
=:
1
x Log@xD
lim
1
xa
xØ+¶
0
se 0 < a § 1
+¶
se a > 1
Non esiste quindi nessun valore di a > 0 per il quale il limite sia finito e diverso da zero; la funzione data è infinitesima di
ordine superiore ad ogni 0 < a § 1, ma inferiore ad ogni a > 1.
3. Generalità sugli infiniti
Iniziamo col dare la definizione di funzione infinita per x Ø x0 .
Definizione 13.3.1
(Funzioni infinite)
Sia X un intervallo, sia x0 œ X , e sia f : X \ 8x0 < Ø  , una funzione definita in X \ 8x0 <. Se risulta:
lim » f @xD » = +¶ ,
si dice che la funzione f @xD è infinita in x0 .
xØ x0
Definizione 13.3.2
(Funzioni infinite)
Sia X un intervallo illimitato superiormente (risp. inferiormente) e sia f : X Ø  una funzione definita in X . Se risulta:
lim » f @xD » = +¶ , (risp. lim » f @xD » = +¶ ),
si dice che la funzione f @xD è infinita per x Ø +¶ (risp. per x Ø -¶ ).
xØ+¶
xØ-¶
Esempio 13.3.1
Ad esempio, le funzioni:
1
1
Å ,
x
Sin@xD2
,
Log@xD,
sono infinite per x Ø 0, mentre le funzioni:
1
x -1
2
1
,
2
,
TanB
px
Log@xD
sono infinite per x Ø 1. Infine, le seguenti funzioni:
x4
x -1
2
,
Log@xD,
sono infinite per x Ø +¶ o per x Ø -¶ (o in entrambe i casi).
Si ha ancora la seguente definizione.
Settembre 2008
‰x ,
2
F,
Carlo Greco
Appunti di Analisi Matematica I
309
13. Infinitesimi e Infiniti
Definizione 13.3.3
(Confronto di infiniti)
Siano f @xD e g@xD due funzioni infinite in x0 .
f @xD
1°) Se risulta:
lim
= 0,
si dice che la funzione g@xD è infinita per x Ø x0 , di ordine superiore rispetto a f @xD.
xØ x0 g@xD
lim À
2°) Se risulta:
À = +¶ ,
f @xD
si dice che la funzione g@xD è infinita per x Ø x0 , di ordine inferiore rispetto a f @xD.
xØ x0
g@xD
lim À
3°) Se risulta:
À= b,
f @xD
dove b è un numero reale diverso da zero, si dice che la funzione f @xD è infinita per x Ø x0 , dello stesso ordine di g@xD.
xØ x0
g@xD
4. Infiniti campione e ordine di infinito
Anche nel caso degli infiniti, si introduce la nozione di infinito campione.
Se x0 œ , la funzione ga @xD =
1
,
…x-x0 »a
dove a è un qualsiasi numero reale maggiore di zero, si dice infinito campione in x0 ;
la funzione ga @xD = » x »a , sempre con a > 0, si dice infinito campione per x Ø ≤¶.
Grazie agli infiniti campione, è possibile introdurre la nozione di ordine di infinito.
(Ordine di infinito 1)
Definizione 13.4.1
Sia f @xD una funzione infinita in x0 , e sia a œ + ; la funzione f @xD si dice infinita di ordine superiore, (risp. di ordine
inferiore) ad a se essa risulta infinita di ordine superiore (risp. di ordine inferiore) alla funzione ga @xD.
La funzione f @xD si dice infinita di ordine a se essa risulta infinita dello stesso ordine di ga @xD.
Esempio 13.4.1
Un polinomio di grado n è un infinito di ordine n per x Ø ≤¶; una funzione razionale fratta
p@xD
q@xD
, dove p@xD e q@xD sono
polinomi di grado n ed m rispettivamente, con n > m, è un infinito di ordine n - m per x Ø ≤¶.
La funzione f @xD =
3
x -
1
2
x è un infinito di ordine Å per x Ø +¶.
La funzione Log@xD è un infinito di ordine minore di
Log@xD
lim
xØ+¶
1ê10
x
1
10
per x Ø +¶, infatti, come si verifica immediatamente, si ha:
1
Åx
H
= lim
xØ+¶
1
10
1
x
10
= 10 lim
-1
1
xØ+¶
1
x
= 0.
10
Diamo infine la seguente definizione.
(Ordine di infinito 2)
Definizione 13.4.2
Sia f @xD una funzione infinita per x Ø x0 . Se per ogni a > 0 essa è infinita di ordine superiore ad a , si dice che f @xD è
infinita di ordine infinitamente grande per x Ø x0 ; analogamente, se per ogni a > 0 essa è infinita di ordine inferiore ad
a , si dice che f @xD è infinita di ordine infinitamente piccolo per x Ø x0 .
Esempio 13.4.2
Ad esempio, le funzioni:
‰x , 10x -x , x ‰x ,
2
sono infinite di ordine infinitamente grande per x Ø +¶; le funzioni:
Log[x], Log[x + 2],
sono infinite di ordine infinitamente piccolo sempre per x Ø +¶.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
310
13. Infinitesimi e Infiniti
5. Esercizi
Esercizio 13.5.1
Calcolare l'ordine dei seguenti infinitesimi.
Log[1+x] per x Ø 0; Tan[ x ] per x Ø 0;
Jx- Å N
Cos@xD
p
2
p
per x Ø Å ;
2
Hx-pL
1+Cos@xD
per x Ø p;
ArcTan@xD - Å per x Ø ≤¶; LogBCosB x FF per x Ø 0;
3
p
2
x - ArcSin@xD per x Ø 0.
Esercizio 13.5.2
Calcolare l'ordine dei seguenti infiniti.
1
ArcCos@xD
Settembre 2008
per x Ø 1;
3
LogBE
x
+ 1F per x Ø +¶.
Carlo Greco
Appunti di Analisi Matematica I
311
14. Integrali impropri
14 Integrali impropri
Nel capitolo sugli integrali definiti abbiamo considerato una funzione f : @a, bD Ø , limitata, e abbiamo dato la
definizione di integrale definito di f @xD esteso all'intervallo @a, bD. Abbiamo anche visto che non tutte le funzioni sono
integrabili (anche se lo sono certamente le funzioni continue e quelle monotone), ma, se una certa funzione f : @a, bD Ø  è
integrabile, l'integrale definito
‡ f @xD „ x
b
a
è l'area (la misura secondo Peano-Jordan) del trapezoide T f , cioé della parte di piano compresa tra l'intervallo @a, bD ed il
grafico di f @xD. Naturalmente, nelle ipotesi assunte in quel capitolo, tale parte di piano è limitata.
Ci proponiamo ora di considerare alcune situazioni in cui T f non è più limitato, come illustrato nella seguente figura:
y
x
In questo caso l'insieme T f non è limitato né "orizzontalmente", perché la funzione f @xD non è definita su un intervallo
limitato, né "verticalmente", a causa della presenza di asintoti verticali.
Ha ancora senso parlare di "area" di T f ? Ci dobbiamo aspettare che essa sia sempre infinita, dato che T f è illimitato?
Ebbene, vedremo che potremo dare ancora un significato naturale alla nozione di area anche per insiemi illimitati, e che
l'area di un insieme di questo tipo non è necessariamente infinita.
E' opportuno osservare che il problema che ci stiamo ponendo non ha certo solo un interesse "geometrico", ma interviene
in molte applicazioni concrete della matematica; ad esempio, nella Teoria della Probabilità, si utilizza l'integrale:
1
p
‡
+¶
‰-x „ x = 1;
2
-¶
la funzione integranda rappresenta, a meno di qualche costante, la Distribuzione Normale di Gauss, rappresentata nella
seguente figura:
f @xD = ‰-x
y
2
x
Nei paragrafi seguenti inizieremo a considerare il caso in cui l'intervallo su cui è data la funzione è del tipo @a, +¶@, per
poi passare a funzioni definite su tutto , come quella della figura precedente, e poi a funzioni dotate di asintoti verticali.
1. Funzioni limitate, intervallo @a, +•@
Per chiarire meglio il problema in questo caso, consideriamo, ad esempio, la funzione f @xD =
rappresentato nella seguente figura:
Settembre 2008
1
x2 +1
, il cui grafico è
Carlo Greco
Appunti di Analisi Matematica I
f @xD =
312
14. Integrali impropri
1
x2 + 1
y
x
Vogliamo attribuire un significato all'integrale:
‡
+¶
f @xD „ x,
1
che chiameremo in seguito integrale improprio di f @xD esteso all'intervallo @1, +¶@. A tale scopo, fissiamo un punto
c œD 1, +¶@, e consideriamo l'integrale definito Ÿ1 f @xD „ x; nel caso della funzione f @xD =
c
1
x2 +1
sappiamo facilmente
calcolarne il valore, che è:
‡ f @xD „ x = ‡
c
1
1
c
p
„ x = ArcTan@cD - ArcTan@1D = ArcTan@cD - Å .
4
1 + x2
1
Tale integrale rappresenta, geometricamente, l'area della regione di piano compresa tra l'intervallo @1, cD sull'asse x, e il
grafico di f @xD:
f @xD =
1
1 + x2
y
1
x
c
Osserviamo ora che, passando al limite per c Ø +¶, si ha:
c
p p p p
lim ‡ f @xD „ x = lim ArcTan@cD - Å = Å - Å = Å ;
cØ+¶ 1
cØ+¶
4 2 4 4
è pertanto naturale definire l'integrale
‡
+¶
f @xD „ x,
1
come il limite, per c Ø +¶, di Ÿ1 f @xD „ x, limite che, in questo caso, vale Å . Il valore dell'integrale improprio Ÿ1
p
c
+¶
4
f @xD „ x
l'intervallo @1, +¶@, e il grafico di f @xD. Nel caso della funzione presa in esame, tale "area" vale, appunto, Å .
può essere interpretato, dal punto di vista geometrico, come "l'area" della regione di piano illimitata compresa tra
p
4
Osserviamo che non sempre le cose vanno come nell'esempio precedente: può capitare infatti che il limite
lim ‡ f @xD „ x
cØ+¶
c
a
sia infinito, o che non esista, nel qual caso l'integrale improprio Ÿa
+¶
f @xD „ x si dice divergente o indeterminato. Inoltre,
talvolta si può desiderare di conoscere se tale limite esiste finito oppure no, senza calcolare esplicitamente l'integrale
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
313
14. Integrali impropri
Ÿa f @xD „ x. Di tali questioni ci occuperemo tra poco.
c
Ricordiamo ora che, se f : X Ø  è una funzione definita in un insieme X , essa si dice limitata se esistono due costanti k1
e k2 tali che, per ogni x œ X , si abbia:
k1 § f @xD § k2 ;
ciò significa, geometricamente, che il grafico di f @xD è tutto compreso nella striscia orizzontale tra le due rette y = k1 e
y = k2 . Evidentemente la presenza di asintoti verticali, ad esempio, esclude che la funzione f @xD sia limitata.
Diamo la seguente definizione.
(Integrale improprio in [a, + •[)
Definizione 14.1.1
Sia f : @a, +¶ @ Ø  una funzione limitata, definita sull'intervallo illimitato @a, +¶ @, integrabile in ogni intervallo
@a, cD Õ @a, +¶ @. Si dice integrale improprio di f @xD esteso all'intervallo @a, +¶ @, il limite:
c
lim Ÿa f @xD „ x,
ed esso si indica col simbolo Ÿa
+¶
f @xD „ x:
cØ+¶
c
lim Ÿ f @xD „
cØ+¶ a
x = Ÿa
+¶
f @xD „ x.
Se tale limite esiste finito, la funzione f @xD si dice integrabile (impropriamente) in @a, +¶ @, e l'integrale improprio
Ÿa f @xD „ x si dice convergente; se invece esso è infinito o non esiste, l'integrale improprio Ÿa
divergente (positivamente o negativamente) o indeterminato.
Esempio 14.1.1
+¶
+¶
Dimostriamo che:
‡
+¶
1
x2
1
„ x = 1.
Infatti, consideriamo un punto c œD 1, +¶@; si ha:
‡
c
1
1
1
„x = 1 - Å ;
c
x2
passando al limite in entrambe i membri:
lim ‡
cØ+¶
c
1
1
„ x = lim 1 - Å = 1,
cØ+¶
c
x2
1
cioé, appunto:
‡
+¶
1
Dunque possiamo dire che l'integrale improprio Ÿ1
+¶ 1
x2
1
x2
„ x = 1.
„ x è convergente, e il suo valore è 1.
Esempio 14.1.2
Dimostriamo che:
‡
+¶
1
1
„ x = +¶.
x
Infatti, consideriamo un punto c œD 1, +¶@; si ha:
‡
c
1
1
„ x = -2 + 2
c;
x
passando al limite in entrambe i membri:
lim ‡
cØ+¶
1
cioé, appunto:
Settembre 2008
c
1
x
„ x = lim I-2 + 2
cØ+¶
c M = +¶,
f @xD „ x si dice, risp.,
Carlo Greco
Appunti di Analisi Matematica I
314
14. Integrali impropri
lim ‡
cØ+¶
c
1
1
In questo caso dunque l'integrale improprio Ÿ1
+¶ 1
„ x = +¶.
x
„ x è divergente.
x
Esempio 14.1.3
Dimostriamo che l'integrale improprio:
‡
+¶
Cos@xD „ x
0
è indeterminato. Infatti, consideriamo ancora un punto c œD 0, +¶@; si ha:
‡ Cos@xD „ x = Sin@cD;
c
0
poiché il limite:
lim ‡ Cos@xD „ x = lim Sin@cD
cØ+¶
cØ+¶
c
0
non esiste, si ha l'asserto.
Diamo ora il seguente esempio, particolarmente importante.
Esempio 14.1.4
Consideriamo la famiglia di funzioni fa @xD =
1
,
xa
con a > 0; ci chiediamo per quali valori di a tali funzioni risultano
integrabili nell'intervallo @1, +¶@. A tale scopo, fissiamo come al solito un punto c œD 1, +¶@, e calcoliamo l'integrale
definito Ÿ1
c 1
xa
„ x; si ha:
‡
1
c
1
xa
„x =
1
-a+1
Ic-a+1 - 1M
se a ∫ 1
se a = 1
Log@cD
Osserviamo ora che
lim c-a+1 =
cØ+¶
+¶
se - a + 1 > 0, cioé 0 < a < 1
0
se - a + 1 < 0, cioé 1 < a
pertanto:
lim ‡
cØ+¶
1
Dunque, l'integrale improprio Ÿ1
+¶ 1
xa
c
1
xa
„x =
+¶
se 0 < a § 1
1
a-1
se a > 1
„ x è convergente se e solo se a > 1; se invece 0 < a § 1, esso è divergente.
L'esempio precedente mostra che la convergenza dell'integrale Ÿa
+¶
f @xD tende a zero all'infinito. Preciseremo questo concetto in seguito.
Settembre 2008
f @xD „ x dipende dalla "velocità" con cui la funzione
Carlo Greco
Appunti di Analisi Matematica I
315
14. Integrali impropri
1
a
c
Ÿ1
+¶ 1
Ÿ1
x1.0
„x = + ¶
6 1
„x
x1.0
= 1.792
y
1
x1.0
x
1 c
Osserviamo ora che non sempre è possibile calcolare esplicitamente l'integrale Ÿa f @xD „ x; questo può accadere sia perché
c
la funzione f @xD può non avere primitive elementarmente calcolabili, oppure, semplicemente, perché il calcolo esplicito è
troppo complicato. Il seguente teorema ci consente talvolta di stabilire se un dato integrale improprio è convergente o no,
anche in tal caso.
Teorema 14.1.1 (Confronto per gli integrali impropri)
Siano f @xD e g@xD due funzioni limitate, definite sull'intervallo @a, +¶ @, e integrabili in ogni intervallo @a, cD Õ @a, +¶ @.
Supponiamo che, per ogni x œ @a, +¶ @, si abbia: 0 § f @xD § g@xD.
Allora, se la funzione g@xD è integrabile in @a, +¶ @, anche la funzione f @xD lo è, e si ha:
+¶
+¶
Ÿa f @xD „ x § Ÿa g@xD „ x.
Dimostrazione. Prendiamo c œD a, +¶@, e osserviamo anzitutto che, essendo 0 § f @xD, la funzione:
F@cD = ‡ f @xD „ x
c
a
è monotona cresente in @a, +¶@; infatti, se consideriamo c1 , c2 œ @a, +¶@, con c1 < c2 , si ha:
F@c2 D = ‡
a
c2
f @xD „ x = ‡
c1
a
f @xD „ x + ‡
c2
c1
cioé:
f @xD „ x ¥ ‡
c1
f @xD „ x = F@c1 D,
a
F@c1 D § F@c2 D.
Per il teorema sul limite delle funzioni monotone, il limite di F@cD per c Ø +¶, esiste certamente, quindi l'integrale
improprio:
‡
+¶
f @xD „ x
a
non può essere indeterminato, ma può essere solo convergente o divergente positivamente. Per completare la
dimostrazione del teorema, basta ora osservare che, per ogni c œD a, +¶@, essendo f @xD § g@xD nell'intervallo @a, cD, per la
prima proprietà di monotonia dell'integrale definito, si ha:
‡ f @xD „ x § ‡ g@xD „ x.
c
a
c
a
Passando al limite in entrambe i membri, e ricordando il teorema sulla conservazione delle disuguaglianze, si ha:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
‡
+¶
a
f @xD „ x § ‡
e quindi la funzione f @xD è integrabile in @a, +¶@. à
Ÿa
316
14. Integrali impropri
+¶
g@xD „ x,
a
f @xD „ x, ma fornisce solo una "stima superiore" del suo valore, attraverso la maggiorazione Ÿa
f @xD „ x § Ÿa
Osservazione. Osserviamo che il teorema precedente non fornisce un metodo per il calcolo dell'integrale improprio
+¶
+¶
+¶
g@xD „ x.
Osservazione. E' importante osservare che l' ipotesi 0 § f @xD § g@xD del teorema precedente può essere alquanto
indebolita; è infatti sufficiente che essa sia soddisfatta almento a partire da un certo x0 œ @a, +¶@ in poi, e non
necessariamente in tutto l'intervallo @a, +¶@.
Esempio 14.1.5
Dimostrare che l'integrale improprio:
‡
xE
+¶ 1 + CosA
1 + x2
0
„x
è convergente, e stimarne il valore.
La funzione integranda in questo caso non è facilmente integrabile; cerchiamo di maggiorarla con una più semplice; si ha,
ad esempio:
0§
1 + CosA x E
1 + x2
da cui, per il teorema precedente:
‡
xE
+¶ 1 + CosA
1 + x2
0
2
§
1 + x2
„x § ‡
+¶
0
,
2
1 + x2
„ x;
il secondo integrale improprio è facilmente calcolabile, e vale p, pertanto possiamo dire che anche l'integrale dato è
convergente, e si ha:
‡
0
+¶ 1 + CosA
xE
1 + x2
„ x § p.
Naturalmente non abbiamo ottenuto il "vero" valore dell'integrale dato, ma solo una maggiorazione per esso. Si potrebbe
dimostrare che, in effetti:
‡
0
+¶ 1 + CosA
xE
1 + x2
„ x = 2.1586 …
Dal teorema precedente scaturisce il seguente criterio di integrabilità.
Teorema 14.1.2 (Criterio dell'infinitesimo per integrali impropri)
Sia f : @a, +¶ @ Ø  una funzione limitata, positiva, e integrabile in ogni intervallo @a, cD Õ @a, +¶ @. Allora:
1°) se f @xD è infinitesima, per x Ø +¶ , di ordine maggiore o uguale ad a , con a > 1, è anche integrabile in @a, +¶ @;
2°) se f @xD è infinitesima, per x Ø +¶ , di ordine minore o uguale ad 1, l'integrale improprio è divergente positivamente.
Dimostrazione. Supponiamo che f @xD sia infinitesima di ordine maggiore o uguale ad un certo a œ , con a > 1; si ha
allora:
lim
xØ+¶
f @xD
1
xa
= b,
con b = 0 oppure con b œ , b > 0. In entrambe i casi, fissato un ¶ > 0, per definizione di limite esiste un certo
x œ @a, +¶@, che possiamo supporre anche maggiore di zero, tale che, per ogni x ¥ x , si abbia:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
317
14. Integrali impropri
f @xD
< b + ¶,
1
xa
da cui:
0 § f @xD <
per ogni x ¥ x,
b+¶
xa
.
Per il teorema del confronto degli integrali impropri, ricordando che la funzione
b+¶
xa
è integrabile se a > 1, si ha
immediatamente la prima affermazione del teorema.
Per dimostrare la seconda affermazione, supponiamo ora che f @xD sia infinitesima di ordine minore o uguale ad 1; si ha
allora:
f @xD
lim
1
xØ+¶
Åx
= b,
con b = +¶ oppure con b œ , b > 0. In entrambe i casi, fissato un numero k , con 0 < k < b, per definizione di limite esiste
un certo x œ @a, +¶@, con anche x > 0, tale che, per ogni x ¥ x , si abbia, questa volta:
f @xD
1
Åx
> k,
cioé:
k
Å < f @xD.
x
E' chiaro allora che la funzione f @xD non può essere integrabile in @a, +¶@, altrimenti, sempre per il teorema del confronto
per gli integrali impropri, tale dovrebbe essere anche la funzione Å1 , mentre invece sappiamo che essa non è
impropriamente integrabile.
+¶
Dunque Ÿa f @xD „ x
x
= +¶, e ciò completa la dimostrazione del teorema. à
Esempio 14.1.6
Adoperando il criterio dell'infinitesimo, dire quali dei seguenti integrali impropri è convergente.
‡
0
x3 + 3
+¶
5x +3x +1
5
2
„ x, ‡
+¶ Sin@xD + Cos@xD + 4 x
0
Il primo è convergente, dato che la funzione
Sin@xD+Cos@xD+4 x
x2 +1
1+x
2
x3 +3
5 x5 +3 x2 +1
„ x, ‡
2
+¶
1
Log@xD
„ x, ‡
+¶
‰-x „ x.
2
0
è infinitesima di ordine 2 all'infinito; invece la funzione
è infinitesima di ordine 1, infatti:
Sin@xD+Cos@xD+4 x
1+x2
1
Åx
=
x
1 + x2
HSin@xD + Cos@xDL +
4 x2
1 + x2
Ø 4,
pertanto il corrispondente integrale improprio è divergente positivamente. La funzione
1
Log@xD
è infinitesima di ordine
2
infinitamente piccolo, quindi l'integrale improprio diverge positivamente; invece la funzione ‰-x è infinitesima di ordine
infinitamente grande, quindi il corrispondente integrale improprio converge.
2. Funzioni limitate, intervalli D - •, aD, e D - •, +•@
Nel paragrafo precedente abbiamo considerato integrali impropri del tipo:
‡
+¶
f @xD „ x;
a
con considerazioni analoghe è possibile definire la nozione di integrale improprio per funzioni definite in intervalli del tipo
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
318
14. Integrali impropri
D - ¶, aD, e i teoremi visti precedentemente continuano ad essere validi anche in tale caso, con ovvie modifiche
nell'enunciato.
Esempio 14.2.1
Calcolare il seguente integrale improprio:
‡
0
x2 ‰x „ x.
-¶
In questo caso utilizziamo la definizione: fissiamo c œD - ¶, 0D, e calcoliamo l'integrale definito:
2 x
‡ x ‰ „ x.
0
c
Integrando per parti, si ha:
2 x
2 x
x
2 x
x
x
2 x
x
x
x 2
‡ x ‰ „ x = x ‰ - ‡ 2 x ‰ „ x = x ‰ - 2 Kx ‰ - ‡ ‰ „ xO = x ‰ - 2 Hx ‰ - ‰ L = ‰ Ix - 2 x + 2M,
pertanto:
2 x
c 2
‡ x ‰ „ x = 2 - ‰ Ic - 2 c + 2M.
0
c
Passando al limite per c Ø -¶, si ha:
‡
0
x2 ‰x „ x = 2.
-¶
Vediamo ora come possiamo definire un integrale improprio esteso a tutto : a tale scopo basterà prendere un punto
qualsiasi a œ , e definire l'integrale Ÿ-¶ f @xD „ x come la somma dei due integrali impropri Ÿ-¶ f @xD „ x + Ÿa
+¶
a
+¶
f @xD „ x,
purché non si abbia +¶ - ¶ o -¶ + ¶.
(Integrale improprio in )
Definizione 14.2.1
Sia f :  Ø  una funzione limitata, integrabile in ogni intervallo chiuso e limitato; se a œ  e se i due integrali impropri:
a
+¶
Ÿ-¶ f @xD „ x e Ÿa f @xD „ x
non sono uno divergente positivamente e l'altro negativamente, si dice integrale (improprio) di f @xD esteso ad  , e si
indica col simbolo Ÿ-¶ f @xD „ x, la somma di tali integrali, cioé si pone:
+¶
Ÿ-¶ f @xD „ x = Ÿ-¶ f @xD „ x + Ÿa f @xD „ x.
Se anche uno solo dei due integrali a secondo membro è indeterminato, si dice indeterminato anche l'integrale improprio
a primo membro. Negli altri casi esso si dirà convergente, o divergente (positivamente o negativamente) a seconda che
tale risulti il secondo membro.
+¶
+¶
a
Osservazione. La definizione appena data è lecita in quanto, come si potrebbe facilmente dimostrare, essa non dipende dal
punto a œ  scelto.
Esempio 14.2.2
Calcolare il seguente integrale improprio esteso ad :
‡
+¶
-¶
1
„ x.
x2 - 2 x + 2
Prendiamo un qualsiasi punto a œ , e calcoliamo, separatamente, i due integrali impropri:
‡
a
1
-¶ x2
-2x+2
„x
e
‡
a
+¶
1
x -2x+2
2
„ x.
A tale scopo, osserviamo che:
‡
pertanto:
Settembre 2008
1
x -2x+2
2
„x = ‡
1
1 + Hx - 1L2
„ x = ArcTan@x - 1D + C,
Carlo Greco
Appunti di Analisi Matematica I
p
„ x = lim HArcTan@a - 1D - ArcTan@c - 1DL = ArcTan@a - 1D + Å ,
cØ-¶
2
-¶ x2 - 2 x + 2
‡
‡
319
14. Integrali impropri
a
+¶
a
1
p
„ x = lim HArcTan@c - 1D - ArcTan@a - 1DL = Å - ArcTan@a - 1D.
cØ+¶
2
x2 - 2 x + 2
1
Dunque:
‡
+¶
-¶
Grafico:
f @xD =
p
p
„ x = KArcTan@a - 1D + Å O + K Å - ArcTan@a - 1DO = p.
2
2
x2 - 2 x + 2
1
1
x2 - 2 x + 2
y
x
3. Funzioni non limitate, intervalli D a, bD, @a, b@, o D a, b@
Diamo la seguente definizione.
(Integrale improprio in ]a, b])
Definizione 14.3.1
Sia f :D a, bD Ø  una funzione definita sull'intervallo limitato D a, bD, integrabile in ogni intervallo @c, bD Õ D a, bD. Si dice
integrale improprio di f @xD esteso all'intervallo @a, bD, il limite:
lim Ÿc f @xD „ x,
b
ed esso si indica ancora col simbolo Ÿa f @xD „ x:
b
cØa
lim Ÿc f @xD „ x = Ÿa f @xD „ x.
b
b
Se tale limite esiste finito, la funzione f @xD si dice integrabile (impropriamente) in @a, bD, e l'integrale improprio
cØa
Ÿa f @xD „ x si dice convergente; se invece esso è infinito o non esiste, l'integrale improprio Ÿa f @xD „ x si dice, risp.,
divergente (positivamente o negativamente) o indeterminato.
Esempio 14.3.1
b
b
Calcolare il seguente integrale improprio:
‡
1
0
La funzione integranda f @xD =
f @xD =
1
x
ha un asintoto per x Ø 0:
1
x
y
1
Settembre 2008
x
1
x
„ x.
Carlo Greco
Appunti di Analisi Matematica I
320
14. Integrali impropri
Utilizziamo la definizione: fissiamo c œD 0, 1D, e calcoliamo l'integrale definito:
‡
1
1
c
„ x,
x
che rappresenta l'area della regione di piano indicata in figura:
f @xD =
1
x
y
c
x
1
L'integrale sull'intervallo @c, 1D si calcola immediatamente:
‡
1
1
c
„x = 2 - 2
c
x
pertanto, passando al limite per c Ø 0, si ha:
lim ‡
cØ0
1
„ x = lim I2 - 2
1
c
c M = 2,
cØ0
x
cioé:
‡
1
0
1
„ x = 2.
x
In questo caso l'integrale improprio considerato è convergente.
Esempio 14.3.2
Generalizziamo ora quanto visto nell'esempio precedente al caso delle funzioni del tipo
1
,
xa
con 0 < a; esse, considerate in
un intervallo del tipo D 0, aD, hanno tutte un asintoto verticale per x Ø 0. Procedendo come nell'esempio precedente,
prendiamo c œD 0, aD; poiché:
‡
1
xa
„x =
‡
c
1
xa
x1-a
Log@xD
si ha:
a
1
1-a
„x =
1
1-a
se a ∫ 1
se a = 1
Ia1-a - c1-a M
Log@aD - Log@cD
se a ∫ 1
se a = 1
Ora, ricordiamo che:
lim c1-a =
cØ0
+¶
se 1 - a < 0, cioé se a > 1
0
se 1 - a > 0, cioé se a < 1
Si ha pertanto:
lim ‡
cØ0
c
a
1
xa
„x =
+¶
1
1-a
se a ¥ 1
a1-a
se 0 < a < 1
Dunque, l'integrale improprio considerato diverge se a ¥ 1 (quindi la funzione integranda è infinita di ordine maggiore o
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
321
14. Integrali impropri
uguale ad 1), converge invece se 0 < a < 1 (la funzione integranda è un infinito di ordine minore di 1).
0.5
a
c
Ÿ0
1 1
Ÿ0.5
1
x0.5
„x = 2.
1
x0.5
„x = 0.585786
y
1
x0.5
c
x
1
Anche per gli integrali impropri considerati in questo paragrafo vale un teorema del confronto e un criterio dell'infinito.
Teorema 14.3.1 (Criterio di confronto per gli integrali impropri)
Siano f @xD e g@xD due funzioni, definite sull'intervallo limitato D a, bD, e integrabili in ogni intervallo @c, bD Õ D a, bD.
Supponiamo che, per ogni x œ D a, bD, si abbia: 0 § f @xD § g@xD.
Allora, se la funzione g@xD è integrabile in @a, bD, anche la funzione f @xD lo è, e si ha:
Ÿa f @xD „ x § Ÿa g@xD „ x.
b
b
Osservazione. Anche per questo teorema è sufficiente che l'ipotesi 0 § f @xD § g@xD sia soddisfatta solo in un intervallo del
tipo D a, b0 @ (cioé solo in un intorno destro di a), invece che in tutto l'intervallo.
Teorema 14.3.2 (Criterio dell'infinito per gli integrali impropri)
Sia f :D a, bD Ø  una funzione limitata, positiva, e integrabile in ogni intervallo @c, bD Õ D a, bD. Allora:
1°) se f @xD è infinita, per x Ø a, di ordine minore o uguale ad a , con a < 1, è anche integrabile in @a, bD;
2°) se f @xD è infinita, per x Ø a, di ordine maggiore o uguale ad 1, l'integrale improprio è divergente positivamente.
Esempio 14.3.3
Applicando il criterio dell'infinito, stabilire quali dei seguenti integrali impropri è convergente.
‡
1
La funzione
1
Log@xD
10
1
Log@xD
‡
„ x;
1
10
x2 + 2
4
‡ H-Log@xDL „ x;
1
„ x;
x-1
0
è infinita di ordine 1 per x Ø 1, pertanto il corrispondente integrale improprio diverge positivamente.
Invece, la funzione
x2 +2
4
x-1
è infinita di ordine Å1 , e l'integrale converge. Infine, la funzione Log@xD è infinita di ordine
4
infinitamente piccolo per x Ø 0, quindi l'integrale improprio considerato converge (in quest'ultimo caso, in effetti, sarebbe
facile calcolarne anche il valore).
Osserviamo infine che, con considerazioni analoghe a quelle sviluppate nei casi precedenti, è facile definire la nozione di
integrale improprio anche nel caso di funzioni definite su intervalli semiaperti del tipo @a, b@, così come anche su intervalli
aperti del tipo D a, b@. In quest'ultimo caso, si considera un qualsiasi punto c œD a, b@, e si considerano i due integrali
impropri:
‡ f @xD „ x, e
c
a
‡ f @xD „ x.
b
c
Se essi non sono uno divergente positivamente e l'altro negativamente, si porrà, per definizione:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
322
14. Integrali impropri
‡ f @xD „ x = ‡ f @xD „ x + ‡ f @xD „ x.
b
c
a
b
a
c
4. Esercizi
Esercizio 14.4.1
Adoperando la definizione, calcolare seguenti integrali impropri.
Ÿ0
+¶
„ x; Ÿ-¶
+¶
1
1+x2
Ÿ0
1 1
Ÿ1
2
Ÿ0
+¶
1
2-x
+¶
„ x; Ÿ0
11
„ x; Ÿ0
2
„ x; Ÿ0
„ x; Ÿ0
+¶ 1
1+x
„ x; Ÿ0 Å „ x; Ÿ0
x
+¶
1
x Log@xD2
Ÿ1
x2
1
1+x2
1 1
9
4-x2
1+x2
„ x;
„ x;
x
„ x; Ÿ0
1
x ‰-
+¶ x
1+x
1
3
„ x;
Hx-1L2
„ x (porre
1 + x2 = t);
‰x -1
+¶ ‰x
+¶
1
„ x; Ÿ-¶ 2 x „ x; Ÿ-¶ 2
„ x;
‰2 x -‰-x
‰ +1
x -2 x+10
Esercizio 14.4.2
Adoperando il criterio di confronto, studiare la convergenza dei seguenti integrali impropri.
‰x
0
0
2
‰ „ x = +¶; Ÿ-1 „ x; Ÿ-¶ ‰x CosAx2 E „ x;
3
Ÿ0
+¶ x2
x
Ÿ1
Hx-1L2
3
1
„x
3-x
Esercizio 14.4.3
Adoperando il criterio dell'infinitesimo o dell'infinito, studiare la convergenza dei seguenti integrali impropri.
Ÿ1
+¶
x-1
„ x; Ÿ0
1
x3 +x+5
Hx-1L2
x
„ x; Ÿ0
+¶ 3
Ÿpê2 Sin@xD „ x; Ÿ0
p
Ÿ1
+¶ Sin@xD2
x2
1
1
„ x; Ÿ0
x3 +1
Ÿ0
+¶
Settembre 2008
„ x; Ÿ1
„ x; Ÿ0
1
pê4
1
3
1
ArcSin@xD
ArcTan@xD
1+x
„ x; Ÿ0
x
2
1
‰x -1
+¶ Cos@xD2
x ‰-
x + x
„ x.
1
Tan@xD
„ x;
„ x;
Log@xD
„ x; Ÿ0
1
1
x Log@xD
„ x;
Carlo Greco
Appunti di Analisi Matematica I
15. La formula di Taylor
323
15 La formula di Taylor
In questo capitolo vedremo come è possibile approssimare una funzione f @xD nelle vicinanze di un punto x0 mediante
polinomi, che vengono detti polinomi di Taylor, generalizzando così quanto si è già visto a proposito della retta tangente in
P0 = Hx0 , f @x0 DL.
1. I polinomi di Taylor e la formula di Taylor col resto di Peano
equazione p1 @xD = f '@x0 D Hx - x0 L + f @x0 D. Il grafico di tale retta, che passa per il punto P0 = Hx0 , f @x0 DL, è infatti quasi
Una funzione derivabile nel punto x0 può essere approssimata in un intorno di tale punto mediante la retta tangente di
identico a quello di f @xD in un piccolo intorno di x0 .
Ad esempio, la tangente al grafico di Log@xD nel punto x0 = 1 è y = x - 1, pertanto Log@xD º x - 1 se x º 1. Si ottiene così
[email protected] º 0.05, il che costituisce un'ottima approssimazione, dato che il "vero" valore di [email protected] è 0.0488 ...
Dato il grande interesse pratico di questo tipo di approssimazioni, è naturale cercare di ottenerne di più soddisfacenti
considerando, ad esempio, parabole passanti per P0 invece che rette. L'equazione di una generica parabola passante per
P0 = Hx0 , f @x0 DL è:
p2 @xD = a Hx - x0 L2 + b Hx - x0 L + f @x0 D.
Infatti, p2 @xD è un polinomio di secondo grado in x (almeno se il coefficiente a ∫ 0), e passa per P0 dato che p2 @x0 D = f @x0 D.
Nella seguente figura sono mostrate alcune di tali parabole, per vari valori dei coefficienti a e b.
a
1
b
1
Tangente Parabola
Parametri Reset
y
f @x0 D
P0
x0
x
p2 @xD = aHx-x0 L2 +bHx-x0 L+f @x0 D
Al fine di ottenere una parabola p2 @xD che approssimi ragionevolmente f @xD nelle vicinanze di P0 , è naturale imporre che:
1°) p2 '@x0 D = f '@x0 D, cioé che sia la funzione f che la parabola p2 @xD abbiano la stessa tangente in P0 ;
2°) p2 ''@x0 D = f ''@x0 D, cioé che la funzione f e la parabola p2 @xD abbiano la stessa convessità o concavità in P0 .
Poiché si ha:
p2 '@xD = 2 a Hx - x0 L + b
p2 ''@xD = 2 a,
le condizioni precedenti si traducono nel sistema:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
15. La formula di Taylor
;
324
p2 '@x0 D = b = f '@x0 D
p2 ''@x0 D = 2 a = f ''@x0 D
che fornisce i seguenti valori per i coefficienti a e b:
b = f '@x0 D
a=
f ''Ax0 E
2
Pertanto la parabola p2 @xD = Å1 f ££@x0 D Hx - x0 L2 + f £ @x0 D Hx - x0 L + f @x0 D non solo passa per il punto P0 , ma ha anche le
prime due derivate coincidenti con quelle di f in x0 . Nella seguente figura è mostrato, oltre al grafico di f @xD, quello della
2
retta tangente p1 @xD, e della parabola p2 @xD = Å f ££@x0 D Hx - x0 L2 + f £ @x0 D Hx - x0 L + f @x0 D.
1
2
p1 @xD
p2 @xD
y
f @x0 D
P0
x
x0
Come si può vedere, l'approssimazione ottenuta mediante la parabola p2 @xD è sensibilmente migliore di quella ottenuta con
la retta tangente. Si capisce, a questo punto, che il passo successivo consiste nel considerare una generica cubica passante
per P0 , la cui equazione è:
p3 @xD = a Hx - x0 L3 + b Hx - x0 L2 + c Hx - x0 L + f @x0 D,
e nel determinare i coefficienti a, b e c in modo che:
p3 '@x0 D = f '@x0 D
p3 ''@x0 D = f ''@x0 D
p3 '''@x0 D = f '''@x0 D
Essendo:
p3 '@x0 D = 3 a Hx - x0 L2 + 2 b Hx - x0 L + c
p3 ''@x0 D = 3 ÿ 2 a Hx - x0 L + 2 b
p3 '''@x0 D = 3 ÿ 2 a
si ottiene facilmente:
c = f '@x0 D
b=
a=
e quindi la cubica cercata è:
p3 @xD =
f '''@x0 D
3!
Hx - x0 L3 +
f ''@x0 D
2
f ''Ax0 E
f '''Ax0 E
2
3!
Hx - x0 L2 + f '@x0 D Hx - x0 L + f @x0 D.
Nella figura seguente si vede il grafico di f @xD (linea spessa), quello di p1 @xD (retta tangente) e quelli di p2 @xD e p3 @xD (risp.
una parabola e una cubica).
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
p1 @xD
p2 @xD
325
15. La formula di Taylor
y
f @x0 D
p3 @xD
P0
x
x0
Le precedenti considerazioni inducono a dare la seguente definizione.
(Polinomio di Taylor)
Definizione 15.1.1
Sia X un intervallo di  , sia x0 œ X , e sia f : X Ø  una funzione derivabile n volte in x0 . Si dice polinomio di Taylor di
ordine n, relativo alla funzione f @xD, di punto iniziale x0 , il polinomio:
pn @xD = ⁄
n
f HkL Ax0 E
k!
Hx - x0 Lk .
Osservazione. Il grado di pn @xD è sempre minore o uguale ad n; è esattamente n se f HnL @x0 D ∫ 0.
k=0
Osservazione. Si ha, evidentemente:
pn @xD = pn-1 @xD +
f HnL @x0 D
n!
Hx - x0 Ln ,
cioé ogni polinomio di Taylor di ordine n si ottiene dal precedente aggiungendo il termine
Osservazione. Si ha immediatamente, per costruzione: pn @x0 D = f @x0 D.
n
f HnL Ax0 E
n!
Hx - x0 Ln .
3
p3 @xD = f @x0 D + f '@x0 DHx-x0 L +
f H2L @x0 D
2
Hx-x0 L2 +
f H3L @x0 D
6
Hx-x0 L3
Vale il seguente teorema, che considera il caso particolare in cui la funzione f @xD è, essa stessa, un polinomio.
Teorema 15.1.1 (Formula di Taylor per i polinomi)
Sia f @xD un polinomio di grado n; allora, se x0 œ  , il polinomio di Taylor di ordine n relativo ad f @xD, di punto iniziale
x0 , coincide con f @xD.
Dunque, se la funzione f @xD è, in particolare, un polinomio di grado n, allora pn @xD = f @xD, come si vede nel seguente
esempio.
Sia f @xD = 2 x3 - x2 + 2 x - 1; scrivere il polinomio di Taylor di ordine 3 relativo ad f @xD, di punto iniziale x0 = 1.
Esempio 15.1.1
Dobbiamo calcolare, anzitutto, il valore della funzione e quello delle sue prime tre derivate nel punto x0 = 1. Si ha:
f H0L @x0 D = 2 f H1L @x0 D = 6 f H2L @x0 D = 10 f H3L @x0 D = 12
quindi:
p3 @xD =
12
3!
Hx - 1L3 +
10
2!
Hx - 1L2 +
6
1!
Hx - 1L + 2 = 2 Hx - 1L3 + 5 Hx - 1L2 + 6 Hx - 1L + 2
Ciò che abbiamo ottenuto, cioé p3 @xD = 2 Hx - 1L3 + 5 Hx - 1L2 + 6 Hx - 1L + 2, non è altro che un modo diverso di scrivere il
polinomio f @xD; infatti, sviluppando i calcoli, si vede subito che 2 Hx - 1L3 + 5 Hx - 1L2 + 6 Hx - 1L + 2 = 2 x3 - x2 + 2 x - 1.
Osserviamo esplicitamente che, avendo calcolato p3 @xD, abbiamo calcolato anche i polinomi pn con n < 3, infatti:
p1 @xD = 6 Hx - 1L + 2
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
326
15. La formula di Taylor
p2 @xD = 5 Hx - 1L2 + 6 Hx - 1L + 2
p3 @xD = 2 Hx - 1L3 + 5 Hx - 1L2 + 6 Hx - 1L + 2.
Osserviamo anche che, essendo f '''@xD = 12, f HkL @xD = 0 per ogni k > 3. In altri termini, la derivata terza di f @xD è costante,
e quindi tutte le sue derivate successive sono nulle. Di conseguenza, i polinomi di Taylor pn @xD, con n > 3, coincidono tutti
con p3 @xD.
Come previsto dal teorema precedente, la stessa circostanza si verifica per qualsiasi polinomio, come si può vedere
nell'animazione che segue.
x2 + 3 x - 5
x0 =
1
p@xD = x2 + 3 x - 5
p0 @xD = -1
p0 @xD = -1
n
0
Naturalmente, se f @xD non è un polinomio, nessun polinomio di Taylor pn @xD potrà essere uguale a f @xD. Posto allora:
rn @xD = f @xD - pn @xD,
si può scrivere:
f @xD = pn @xD + rn @xD.
La formula precedente rappresenta una decomposizione della funzione f @xD nella somma del polinomio di Taylor di ordine
n e di un "resto" rn @xD, che rappresenta, ovviamente, l'errore che si commette approssimando la funzione data con pn @xD.
La decomposizione f @xD = pn @xD + rn @xD viene chiamata formula di Taylor di ordine n, e rn @xD si dice, appunto, resto
n-esimo della formula di Taylor.
Nel caso in cui x0 = 0, la formula di Taylor viene talvolta chiamata formula di McLaurin.
Il seguente teorema precisa in che senso il polinomio pn @xD approssima "bene" la funzione f @xD nelle vicinanze del punto
x0 .
Teorema 15.1.2 (Resto n-esimo della formula di Taylor)
Sia X un intervallo di  , x0 œ X , e sia f : X Ø  una funzione derivabile n volte in x0 . Si ha allora:
lim
f @xD- pn @xD
Ix- x0 Mn
= 0,
dove pn @xD è il polinomio di Taylor di ordine n relativo alla funzione f @xD, di punto iniziale x0 .
xØ x0
Dimostrazione. Poiché pn @x0 D = f @x0 D, il limite:
lim
xØx0
f @xD - pn @xD
Hx - x0 Ln
0
si presenta nella forma indeterminata Å . Per dimostrare che tale limite è uguale a zero, applichiamo n - 1 volte la regola
0
dell'Hôpital:
lim
xØx0
Ora, osserviamo che, ovviamente:
Settembre 2008
f @xD - pn @xD
Hx - x0 Ln
= lim
xØx0
f Hn-1L @xD - pn Hn-1L @xD
DHn-1L @Hx - x0 Ln D
DHn-1L @Hx - x0 Ln D = n! Hx - x0 L.
.
Carlo Greco
Appunti di Analisi Matematica I
327
15. La formula di Taylor
Inoltre, essendo pn @xD un polinomio di grado n, si ha:
pn Hn-1L @xD = n!
f HnL @x0 D
n!
Hx - x0 L + Hn - 1L!
f Hn-1L @x0 D
Hn - 1L!
= f HnL @x0 D Hx - x0 L + f Hn-1L @x0 D.
In definitiva, applicando n - 1 volte la regola dell'Hôpital, si ottiene:
lim
lim
f Hn-1L @xD - pn Hn-1L @xD
xØx0
D
Hn-1L
@Hx - x0 L D
n
f @xD - pn @xD
Hx - x0 Ln
xØx0
= lim
=
f Hn-1L @xD - f HnL @x0 D Hx - x0 L - f Hn-1L @x0 D
n! Hx - x0 L
xØx0
=
1
n!
lim
xØx0
f Hn-1L @xD - f Hn-1L @x0 D
x - x0
H*L
- f HnL @x0 D = 0.
L'ultima uguaglianza, indicata con H*L, è dovuta al fatto che, essendo la funzione f @xD derivabile n volte nel punto x0 , si ha,
ovviamente:
f Hn-1L @xD - f Hn-1L @x0 D
lim
x - x0
xØx0
= f HnL @x0 D,
e pertanto il teorema è dimostrato. à
Dunque il teorema precedente afferma che il resto n -esimo rn @xD non solo tende a zero per x Ø x0 , ma è addirittura
infinitesimo di ordine superiore a Hx - x0 Ln per x Ø x0 . Possiamo pertanto scrivere:
f @xD = pn @xD + o@Hx - x0 Ln D.
Osservazione. Nelle ipotesi del teorema precedente, possiamo considerare la funzione w : X Ø  così definita:
f @xD-pn @xD
Ix-x0 M
n
w@xD =
0
se x ∫ x0
se x = x0
Tale funzione è ovviamente continua in tutto X , compreso il punto x0 proprio grazie al teorema precedente, e risulta:
w@xD Hx - x0 Ln = rn @xD in X,
infatti, se x ∫ x0 , ciò è vero perché w@xD =
f @xD- pn @xD
Ix-x0 Mn
; se invece x = x0 , si ha w@x0 D = 0 = rn @x0 D.
Dunque, come ovvio corollario del teorema precedente, si ha quanto segue.
Teorema 15.1.3 (Formula di Taylor con il resto di Peano)
Sia X un intervallo di  , x0 œ X , e sia f : X Ø  una funzione derivabile n volte in x0 . Esiste allora una funzione
continua w : X Ø  , con w @x0 D = 0, tale che:
f @xD = pn @xD + w @xD Hx - x0 Ln ,
dove pn @xD è il polinomio di Taylor di ordine n relativo alla funzione f @xD, di punto iniziale x0 .
In altri termini, il teorema precedente afferma che il resto n -esimo rn @xD della formula di Taylor può essere scritto nella
forma rn @xD = w@xD Hx - x0 Ln , che viene appunto detta "di Peano".
2. Esercizi
Dato il polinomio f @xD = x3 - 3 x2 + 2, scrivere i polinomi di Taylor di ordine 3 relativi ad f @xD, di punti iniziali,
Esercizio 15.2.1
(Polinomi)
rispettivamente, x0 = -1 e x0 = 2, e controllare che entrambe coincidono con la funzione data.
Esercizio 15.2.2
Scrivere i primi tre addendi non nulli dei polinomi di Taylor di punto iniziale x0 , relativi alle seguenti funzioni.
f @xD = ArcTan@xD, con x0 = 0;
f @xD = Log@xD, con x0 = 1;
f @xD = x Cos@xD, con x0 = 0.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
328
15. La formula di Taylor
Data la funzione f @xD = ArcTan@xD, scriverne il polinomio di Taylor p3 @xD di punto iniziale x0 = 0. Tracciare inoltre il
(Formula di Taylor)
grafico di f @xD insieme con quelli di p1 @xD, p2 @xD e p3 @xD.
Esercizio 15.2.4
Sia f @xD =
1
;
1-x
(Resto)
scrivere il polinomio di Taylor p3 @xD di punto iniziale x0 = 0, e verificare, mediante il calcolo diretto, che:
lim
xØx0
Esercizio 15.2.5
f @xD - p3 @xD
Hx - x0 L3
= 0.
(Resto)
Giustificare la seguente formula:
‰x = 1 + x +
x2
2
+
x3
6
+ oAx3 E.
Scrivere il polinomio di Taylor p5 @xD di punto iniziale x0 = 0, relativo alla funzione f @xD = Sin@xD e alla funzione
Esercizio 15.2.6
(Sin@xD e Cos@xD)
g@xD = Cos@xD.
3. Il test della derivata n-esima per i punti di minimo, massimo e flesso
Tra le varie applicazioni della formula di Taylor col resto di Peano, vista nei paragrafi precedenti, vi è un teorema che
riguarda la possibilità di studiare i punti di massimo, di minimo o di flesso di una funzione f @xD, calcolando le derivate
successive di f @xD in tali punti. Si ha infatti il seguente teorema.
Teorema 15.3.1 (Test della derivata n-esima)
Sia X un intervallo di  , x0 un punto interno ad X , e sia f : X Ø  una funzione derivabile n volte in x0 . Supponiamo che
si abbia:
f ''@x0 D = ∫ = f Hn-1L @x0 D = 0, e f HnL @x0 D ∫ 0.
Si ha allora che, se n è pari, f @xD è convessa o concava in x0 a seconda che sia f HnL @x0 D > 0, oppure f HnL @x0 D < 0; se
invece n è dispari, il punto x0 è di flesso.
In particolare, se anche f '@x0 D = 0, se n è pari, f @xD ha un punto di minimo o di massimo relativo proprio in x0 a seconda
che sia f HnL @x0 D > 0, oppure f HnL @x0 D < 0; se invece n è dispari, il punto x0 è di flesso a tangente orizzontale.
Dimostrazione. Poiché f @xD è derivabile n volte in x0 , per la formula di Taylor col resto di Peano, si ha:
f @xD = pn @xD + w@xD Hx - x0 Ln ,
dove pn @xD è il polinomio di Taylor relativo alla funzione f @xD, di punto iniziale x0 , e w@xD è una funzione continua che si
annulla in x0 . Ciò premesso, passiamo alla dimostrazione del teorema. Supponiamo dunque che si abbia:
f ''@x0 D = ∫ = f Hn-1L @x0 D = 0, e f HnL @x0 D ∫ 0.
Dunque tutte le derivate della funzione, a partire dalla seconda, fino a quella di ordine n - 1, si annullano nel punto x0 ,
mentre f HnL @x0 D ∫ 0. In tal caso il polinomio pn @xD si riduce ad essere:
f @xD = f @x0 D + f '@x0 D Hx - x0 L +
pertanto si ha:
f @xD = f @x0 D + f '@x0 D Hx - x0 L +
f HnL @x0 D
n!
da cui:
f @xD - Hf '@x0 D Hx - x0 L + f @x0 DL =
f HnL @x0 D
n!
Hx - x0 Ln ,
Hx - x0 Ln + w@xD Hx - x0 Ln ,
f HnL @x0 D
n!
+ w@xD Hx - x0 Ln .
Osserviamo che la funzione tra parentesi nel primo membro, cioé y = f '@x0 D Hx - x0 L + f @x0 D, non è altro che la tangente al
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
329
15. La formula di Taylor
grafico di f @xD nel punto di ascissa x0 . Supponiamo ora, ad esempio, che n sia pari e che f HnL @x0 D > 0; essendo w@x0 D = 0,
per il teorema della permanenza del segno, esiste un intorno I di x0 , tale che, per ogni x œ I › X , si abbia:
f HnL @x0 D
n!
+ w@xD > 0.
Pertanto, essendo n pari, si ha, sempre per ogni x œ I › X :
f @xD - Hf '@x0 D Hx - x0 L + f @x0 DL =
Dunque, per ogni x œ I › X \ 8x0 <, si ha:
f HnL @x0 D
n!
+ w@xD Hx - x0 Ln
:
> 0 se x ∫ 0
= 0 se x = 0
f @xD > f '@x0 D Hx - x0 L + f @x0 D,
e ciò dimostra che f @xD è convessa nel punto x0 . In modo analogo si dimostrano le altre affermazioni del teorema. à
Dal teorema precedente discende immediatamente il seguente corollario.
Teorema 15.3.2 (Minimi, massimi, flessi)
Sia X un intervallo di  , x0 un punto interno ad X , e sia f : X Ø  una funzione derivabile 3 volte in x0 . Supponiamo che
si abbia:
f '@x0 D = 0, e f ''@x0 D ∫ 0.
Si ha allora che il punto x0 è di minimo o di massimo relativo proprio a seconda che sia f ''@x0 D > 0, oppure f ''@x0 D < 0.
Se invece:
f ''@x0 D = 0, e f ''' @x0 D ∫ 0,
il punto x0 è di flesso.
Esempio 15.3.1
Consideriamo la funzione f @xD =
Calcoliamo la derivata prima:
x4
4
+ CosAx2 E.
f '@xD = x3 - SinAx2 E 2 x = x Ix2 - 2 SinAx2 EM.
E' immediato osservare che f '@0D = 0, mentre non è altrettanto semplice determinare la natura di questo punto critico
attraverso lo studio del segno della derivata prima; infatti lo studio del segno del fattore x2 - 2 SinAx2 E comporta la
risoluzione di una disequazione trascendente.
Per studiare la natura del punto x = 0 calcoliamo le derivate seconda, terza e quarta in tale punto. Si ha:
f ''@xD = x2 + x I2 x - 4 x CosAx2 EM - 2 SinAx2 E;
f '''@xD = 4 x - 8 x CosAx2 E + x I2 - 4 CosAx2 E + 8 x2 SinAx2 EM;
f H4L @xD = 6 - 12 CosAx2 E + 24 x2 SinAx2 E + x I16 x3 CosAx2 E + 24 x SinAx2 EM
Pertanto:
f ''@0D = 0,
f '''@0D = 0,
f H4L @0D = -6.
Dunque, essendo n pari, e f H4L @0D < 0, l'origine è un punto di massimo relativo proprio per f @xD.
Nelle sezioni precedenti abbiamo visto che, sotto opportune ipotesi, si ha la possibilità di "decomporre" una funzione f @xD
4. La formula di Taylor con il resto di Lagrange
nella somma del polinomio di Taylor pn @xD e di un "resto" che tende a zero velocemente, tanto più quanto più è grande n.
Ciò fornisce la possibilità di approssimare f @xD col polinomio pn @xD nelle vicinanze del punto x0 ; tuttavia, affinché tale
approssimazione sia utile, è necessario saper stimare l'errore che si commette in tale approssimazione. Per questo motivo
diamo un'altra versione della formula di Taylor, detta formula di Taylor col resto di Lagrange, utile a tale scopo.
Teorema 15.4.1 (Formula di Taylor con il resto di Lagrange)
Sia X un intervallo di  , x0 œ X , e sia f : X Ø  una funzione di classe C Hn+1L HX L, cioé derivabile n + 1 volte in X , con
derivata f Hn+1L @xD continua. Per ogni x œ X , con x ∫ x0 , esiste un opportuno punto c, appartenente all'interno
dell'intervallo di estremi x0 ed x, tale che:
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
330
15. La formula di Taylor
f @xD = pn @xD +
f Hn+ 1L @cD
Hn+1L!
Hx - x0 Ln+1 ,
dove pn @xD è il polinomio di Taylor di ordine n relativo alla funzione f @xD, di punto iniziale x0 .
Il teorema precedente afferma dunque che l'errore che si commette approssimando f @xD con pn @xD, è uguale al resto di
Lagrange:
f Hn+1L @cD
Hn + 1L!
Hx - x0 Ln+1 .
In tale espressione compare la quantità Hx - x0 Ln+1 che è nota (perché sono dati x0 , x ed n), e compare la quantità f Hn+1L @cD,
cioé la derivata di ordine n + 1 di f @xD calcolata in un opportuno punto c intermedio tra x0 ed x. Quest'ultimo punto c non è
noto, tuttavia in molti casi è possibile stimare ugualmente f Hn+1L @cD, come si vede negli esempi seguenti.
Esempio 15.4.1
Vogliamo utilizzare la formula di Taylor col resto di Lagrange per calcolare il valore della costante numerica ‰, cioé del
numero di Nepero. A tale scopo, consideriamo la funzione f @xD = ‰x , prendiamo x0 = 0, x = 1, e scriviamo la formula di
Taylor col resto di Lagrange in questa situazione. Si ha:
f @xD = pn @xD +
f Hn+1L @cD
Hn + 1L!
Hx - x0 Ln+1
f @1D = pn @1D +
ï
‰c
Hn + 1L!
ï
‰ = pn @1D +
‰c
Hn + 1L!
,
cioé:
‰ = pn @1D +
‰c
Hn + 1L!
,
dove c œD 0, 1@ è un punto opportuno. Nel secondo membro di questa espressione compare il polinomio di Taylor pn @xD
calcolato per x = 1, cioé:
pn @1D = ‚
n
k=0
compare inoltre la quantità
‰c
Hn+1L!
f HkL @0D
H1 - 0Lk = ‚
n
k!
k=0
1
k!
;
, che rappresenta l'errore che si commette approssimando ‰ con la quantità ⁄nk=0
1
.
k!
Osservando che 0 < ‰c < ‰ < 3, si ha:
0<
‰c
Hn + 1L!
<
Hn + 1L!
3
.
In definitiva:
0 < ‰ -‚
n
k=0
1
k!
<
Hn + 1L!
3
.
Ad esempio, se si vuole calcolare il valore numerico di ‰ con un errore minore di
1
,
1 000 000
si deve anzitutto trovare n in
modo che:
Hn + 1L!
3
<
1
1 000 000
,
cioé Hn + 1L! > 3 000 000, e, a tale scopo, basta prendere n = 9, infatti 10 != 3 628 800. Scrivendo poi la formula precedente
con n = 9, si ha:
0 < ‰ -‚
9
k=0
cioé:
Settembre 2008
1
k!
<
3
10!
Carlo Greco
Appunti di Analisi Matematica I
331
15. La formula di Taylor
0<‰ -
98 641
36 288
<
1
<
1 209 600
1
1 000 000
0 < ‰ - 2.71828 < 8.2672 µ 10-7
Dunque il numero 27 182 815 è una approssimazione di ‰ esatta a meno di un milionesimo, cioé fino alla sesta cifra dopo la
virgola. Il "vero" valore di ‰ è infatti:
‰ = 2.718 281 828 459 045 235 360 287 471 352 662 497 757 247 093 699 959 574 966 97……
e si può ottenere con una precisione grande a piacere, aumentando il valore di n.
In questo esempio ci proponiamo di approssimare la funzione f @xD = Sin@xD con un opportuno suo polinomio di Taylor, di
Esempio 15.4.2
punto iniziale x0 = 0, in tutto l'intervallo A0, Å E. A tale scopo, prendiamo un x œD 0, Å E, e scriviamo la formula di Taylor:
p
2
f @xD = pn @xD +
f Hn+1L @cD
Hn + 1L!
p
2
Hx - x0 Ln+1
Sin@xD = pn @xD +
ï
f Hn+1L @cD
Hn + 1L!
xn+1 .
dove c è un punto intermedio tra zero ed x. Osserviamo ora che f Hn+1L @cD = ≤Sin@cD, oppure f Hn+1L @cD = ≤Cos@cD, pertanto
… f Hn+1L @cD … < 1; poiché anche xn+1 < I Å M
p n+1
2
, si ha, per ogni x œ A0, Å E:
p
» Sin@xD - pn @xD » =
Hn+1L
@cD
Hn + 1L!
f
2
p n+1
KÅ O .
Hn + 1L! 2
1
xn+1 <
Supponiamo ora di voler approssimare f @xD = Sin@xD con pn @xD a meno di
1
100
in tutto l'intervallo A0, Å E; bisognerà
anzitutto prendere n in modo che sia:
p n+1
1
KÅ O <
,
Hn + 1L! 2
100
1
il che si verifica per n = 6:
p n+1 n=6 1 p 7
=
KÅ O
K Å O = 0.00468175 < 0.01;
Hn + 1L! 2
7! 2
1.
si ha dunque, per ogni x œ A0, Å E;
p
2
Sin@xD - p6 @xD <
Il polinomio p6 @xD scritto esplicitamente, è:
p6 @xD = x -
x3
6
+
1
100
x5
120
.
;
nella seguente figura sono messi a confronto il grafico di Sin@xD e quello di p6 @xD (linea tratteggiata).
y
1
x
p
Å2
Come si vede, nell'intervallo A0, Å E, non vi è quasi differenza visibile tra i due grafici.
p
2
Settembre 2008
p
2
Carlo Greco
Appunti di Analisi Matematica I
15. La formula di Taylor
332
Esercizi
Esercizio 15.5.1
Usando il test della derivata n -esima, studiare le seguenti funzioni nel punto x0 indicato.
f @xD = ‰x - 1 - x2 in x0 = 0;
2
f @xD = x + Sin@xD3 in x0 = p.
Data f @xD = Cos@xD, scrivere il polinomio di Taylor p7 @xD, di punto iniziale x0 = 0; utilizzando poi la formula ti Taylor col
Esercizio 15.5.2
resto di Lagrange, stimare la differenza p7 @xD - Cos@xD nell'intervallo @-1, 1D.
Settembre 2008
Carlo Greco
Appunti di Analisi Matematica I
16. Indici
333
16 Indici
1. Indice analitico
I numeri di pagina in grassetto e in colore verde si riferiscono alle definizioni, quelli in corsivo e in colore marrone ai
teoremi; tutti gli altri a parole contenute nel testo.
Accelerazione ... 211
Interi relativi ... 28
Affettare e sommare ... 266
Intersezione di grafici ... 198
Allineamenti decimali ... 28
Intersezione di insiemi ... 10
Angoli notevoli ... 97, 99, 101, 103
Intervalli ... 10
Antiderivata ... 272, 273, 273
Intervallo ampliato ... 151
Antiderivate ... 279
Intorno Hsinistro o destroL di un punto ... 151
Appartiene ... 7
Approssimazione numerica degli zeri ... 196
Ipotesi e tesi ... 8
Approssimazioni ... 323, 214
Irrazionalità di radice di 2 ... 8
Arcocosecante ... 105
Lagrange ... 228, 329
Arcocotangente ... 105
Limite a destra ... 149
Arcosecante ... 105
Limite a sinistra ... 148
Area ... 258, 259
Limite che non esiste ... 147, 148
Area di un insieme illimitato ... 311
Limite Hdef . generaleL ... 151
Area di un plurirettangolo ... 258
Limite delle funzioni composte ... 162
Area settore circolare ... 170
Limite delle successioni monotone ... 178
Aritmetica nell' insieme dei numeri reali ampliato ... 154
Limite di H1 - Cos@xDL ê x ^2 ... 171
Asintoti obliqui ... 164
Asintototi orizzontali ... 145
Asintototi verticali ... 144
Bolzano ... 197
Calcolo del limite per sostituzione ... 157
Cauchy ... 266
Cerchio goniometrico ... 119
Classe di una funzione ... 211
Classi contigue ... 258
Codominio ... 14, 52
Limite di H1 + 1 ê xL^ x ... 182, 183
Limite di H1 + xL^ 1 ê x ... 183
Limite di HH1 + xL^a - 1L ê x ... 184
Limite di ArcSin@xD ê x ... 171
Limite di ArcTan@xD ê x ... 171
Limite di Ha ^ x - 1L ê x ... 183
Limite di a ^x ê x ^a ... 184
Limite di Log@1 + xD ê x ... 183
Limite di Log@xD ê x ^a ... 184
Limite di Sin@xD ê x ... 170
Complementare di un insieme ... 10
Limite di Hx ^aL Log@xD ... 184
Concavità ... 236, 235, 328
Limite finito in più o meno infinito ... 144
Coefficiente angolare ... 38, 201
Limite di successioni ... 177
Condizione necessaria e sufficiente ... 8
Limite finito in un punto ... 138
Confronto di infiniti ... 309
Limite infinito in più o meno infinito ... 146
Confronto per gli integrali impropri ... 315
Limite infinito in un punto ... 143
Confronto per le funzioni ... 168, 169
Limiti delle funzioni elementari ... 153
Confronto per le successioni ... 178, 179
Limiti notevoli ... 170, 170
Confronto tra infinitesimi ... 303
Logaritmi neperiani ... 93
Connettivi logici ... 22
Maggioranti ... 51
Conservazione delle disuguaglianze ... 167
Matematica Finanziaria ... 180
Continuità delle funzioni derivabili ... 206
Media ... 270
Convessità ... 236, 235, 328
Metodo del completamento del quadrato ... 289
Coppie ordinate ... 11, 35
Metodo di esaustione ... 258
Cosecante ... 104
Metodo grafico ... 128
Cotangente ... 104
Minimo HmassimoL assoluto ... 191, 193
Criterio dell' infinitesimo per gli integrali impropri ... 316
Minoranti ... 51
Criterio dell' infinito per gli integrali impropri ... 321
Minuti ... 94
Criterio di confronto per gli integrali impropri ... 321
Misura ... 258, 259
Derivata a sinistra Ha destraL ... 203, 240, 203
Monomio dominante ... 155
Derivata ... 201
Misura di un angolo ... 94
Derivata del logaritmo ... 215
Negazione di una proposizione ... 8
Derivata di ArcCos@xD ... 216
Nepero ... 92, 180, 93
Derivata di ArcSin@xD ... 216
Numeri complessi ... 31
Derivata di ArcTan@xD ... 216
Numeri razionali ... 28, 28
Derivata di a ^x e di ‰^ x ... 215
Numeri trascendenti ... 180
Derivata di f @xD^ g@xD ... 218
Operazioni con funzioni periodiche ... 105
Derivata di Sin@xD ... 215
Operazioni con i limiti ... 154
Derivata di Cos@xD ... 216
Settembre 2008
Intorno di ≤ ¶ ... 151
Numero di Nepero ... 92, 180, 93
Derivata di Tan@xD ... 216
Operazioni con le derivate ... 207
Derivata di x ^a ... 214
Operazioni con le funzioni continue ... 186
Derivata infinita ... 204
o piccolo ... 305
Derivata seconda ... 209
Ordine di infinito ... 309
Derivate delle funzioni elementari ... 205, 217
Ordine di un infinitesimo ... 306
Derivate delle funzioni elementari generalizzate ... 217
Ordine infinitamente grande o piccolo di infinito ... 309
Carlo Greco
Appunti di Analisi Matematica I
Derivate successive ... 209
Ordine infinitamente grande HpiccoloL di infinitesimo ... 307
Derivazione delle funzioni composte ... 208
Parcheggio ... 41, 44
Differenza di due primitive ... 273
Parte immaginaria ... 32
Dimostrazione per assurdo ... 8
Parte intera ... 181
Dirichlet ... 265
Parte reale ... 32
Discontinuità di prima specie ... 186
Peano - Jordan ... 259
Discontinuità di seconda specie ... 186
Pendenza ... 201
Discontinuità eliminabile ... 186
Pendenza infinita ... 40
Discriminante ... 66
Periodo ... 47
Disequazioni equivalenti ... 65
Periodo minimo ... 49, 49, 105
Disequazioni incompatibili ... 82
Permanenza del segno per i limiti ... 166
Distribuzione Normale ... 311
Permanenza del segno per le funzioni continue ... 189
Divisione dei polinomi ... 294
Per ogni ... 9
Elemento di separazione ... 30, 90, 91
Plurirettangolo ... 258
Elemento di un insieme ... 7
Plurirettangolo circoscritto ... 260
Erf @xD ... 302
Polinomi ... 155, 325
Errore ... 212
Polinomio di grado n ... 72
Esiste ... 9
Polinomio di Taylor ... 325
Esiste uno ed un solo ... 9
Potenza con esponente reale ... 90
Equazione trascendente ... 128
Plurirettangolo inscritto ... 260
Fattore differenziale ... 286
Potenza del continuo ... 21
Fattore finito ... 286
Potenza dell' insieme delle parti ... 21
Fermat ... 225
Potenza minore ... 21
Forma indeterminata 0 ê 0 ... 201
Predicato ... 65
Flesso ... 236, 329, 328
Predicati ... 9
Forma indeterminata della somma ... 154
Prezzi benzina ... 44
Forma indeterminata del prodotto ... 155
Primitiva ... 272, 273, 273
Forma indeterminata b ê 0 ... 155, 159, 160
Principio di identità dei polinomi ... 291
Forma indeterminata del quoziente ... 155
Primitive ... 279
Forme indeterminate per f @xD ^g@xD ... 176
Prodotto cartesiano di insiemi ... 11
Formula del cambiamento di base ... 113
Progressione aritmetica ... 62
Forme indeterminate ... 154, 176, 160
Prodotto di una funzione infinitesima per una limitata ... 173
Formula di integrazione per decomposizione ... 283
Progressione geometrica ... 62
Formula di integrazione per parti ... 286
Prolungamento per continuità di una funzione ... 189
Formula di integrazione per sostituzione ... 299
Proprietà dell' addizione ... 29
Formula di McLaurin ... 326
Proprietà della moltiplicazione ... 29
Formula di Taylor ... 326, 327, 329
Proprietà di completezza ... 30, 91
Formula ridotta ... 69
Punto angoloso o cuspidale ... 205
Formule parametriche ... 121
Punto critico ... 225
Formule trigonometriche ... 97, 103
Punto di minimo HmassimoL relativo ... 224
Punto di flesso ... 236
FresnelC@xD ... 302
Punto di minimo HmassimoL relativo proprio ... 224, 329
FresnelS@xD ... 302
Radianti ... 94
Frazione generatrice ... 28
Funzione ... 37
Radice ennesima ... 29
Funzione arcocoseno ... 100
Radici razionali ... 72, 73, 72
Funzione arcoseno ... 98
Ragione ... 62
Funzione arcotangente ... 104
Rapporto incrementale ... 201
Funzione bigettiva ... 17
Regola dei segni ... 67
Funzione composta ... 17
Regola dell' Hôpital ... 219
Funzione coseno ... 96
Regola di Ruffini ... 73
Funzione degli errori ... 302
Resto della formula di Taylor ... 326
Funzione di Dirichlet ... 265
Resto di Lagrange ... 329
Funzione esponenziale ... 91, 91, 181
Resto di Peano ... 327
Funzione ingettiva ... 53, 15
Resto n - esimo della formula di Taylor ... 326
Funzione integrale ... 273, 276
Restrizione ... 37
Funzione integranda ... 266
Restrizione di una funzione tra insiemi ... 19, 37
Funzione inversa ... 54, 17
Rettangolo ... 258
Funzione logaritmo ... 92, 94
Retta secante ... 200
Funzione pari o dispari ... 47
Retta tangente ... 200, 213, 214
Funzione periodica ... 48, 47
Ricerca del minimo e del massimo assoluto ... 226
Funzione potenza di esponente a ... 176
Risolvere una disequazione ... 65
Funzione seno ... 96
Funzione Sin@1 ê xD ... 147
Rolle ... 227
Funzione surgettiva ... 53, 14
Salto ... 186
Funzione tangente ... 102
Secante ... 104
Ruffini ... 73
Funzione tra insiemi ... 12
Secondi ... 94
Funzioni composte ... 162, 208
Segno ... 159, 42
Funzioni continue ... 157, 186, 158,
158, 186, 194, 197, 197, 265, 270, 193
Sign@xD ... 43, 159
Funzioni convesse HconcaveL ... 235
Funzioni crescenti HdecrescentiL ... 61
Settembre 2008
16. Indici
Simmetrie ... 47
SinIntegral@xD ... 302
334
Carlo Greco
Appunti di Analisi Matematica I
Funzioni discontinue ... 186, 186, 186
Somma dei primi n termini di una progressione geometrica ... 62
Funzioni elementari ... 205, 217
Somma di Cauchy ... 266
Funzioni illimitate ... 192
Somma di una funzione divergente e una limitata ... 174
Funzioni infinite ... 308, 308
Somma inferiore ... 260
Funzioni infinitesime ... 303, 303, 173
Somma superiore ... 261
Funzioni integrabili ... 261
Sottoinsieme di un insieme ... 7
Funzioni integrabili elementarmente ... 301
Sottoinsieme proprio di un insieme ... 8
Funzioni irrazionali ... 163
Spazio percorso ... 267
Funzioni limitate ... 173, 51
Studio dei punti angolosi o cuspidali ... 238, 242
Funzioni maggioranti ... 169
Successioni HstrettamenteL crescenti HdecrescentiL ... 63
Funzioni minoranti ... 169
Funzioni razionali ... 156, 160
Funzioni strettamente crescenti HdecrescentiL ... 60
Settembre 2008
16. Indici
Successioni ... 62
Successioni HstrettamenteL monotone ... 63, 178
Funzioni speciali ... 302
Suddivisioni di un intervallo ... 260
Funzioni HstrettamenteL monotone ... 61, 230, 265
Tangente a sinistra Ha destraL ... 203
Gauss ... 311, 302
Tangente verticale ... 204
Grado ... 94
Tasso di interesse ... 180
Grafico ... 37
Tavola degli integrali immediati ... 280
Grafico di una funzione tra insiemi ... 14
Tavola degli integrali immediati generalizzati ... 282
Tabella di verità ... 22
Grafico di Venn ... 10
Taylor ... 325, 325
Hôpital ... 219
Teorema di esistenza ... 193
Implicazione ... 8, 23
Teorema fondamentale dell' algebra ... 32
Infinitesimi campione ... 306
Teoria della Probabilità ... 311
Infiniti campione ... 309
Test della derivata n - esima ... 328
Insieme dei numeri reali ampliato ... 151
Test per i punti di minimo o massimo relativo ... 232
Insieme delle parti ... 8, 21
Titolo ... 1
Insieme di arrivo ... 13
Trapezopide ... 259
Insieme di definizione ... 37
Trinomio ... 66
Insieme di partenza ... 13, 37
Unicità del limite ... 152
Insieme infinito ... 19
Unione di insiemi ... 10
Insiemi contigui ... 30, 90, 258, 91, 259
Unità immaginaria ... 32
Insiemi equipotenti ... 19
Valore assoluto ... 42
Insiemi numerabili ... 20
Valori intermedi ... 197
Insiemi separati ... 30
Valor medio ... 271
Insiemi uguali ... 7
Variabile apparente ... 267
Integrabilità delle funzioni continue ... 265
Variabile dipendente ... 35
Integrabilità delle funzioni monotone ... 265
Variabile indipendente ... 35
Integrale definito ... 268, 277, 261
Velocità istantanea ... 211
Integrale improprio ... 312, 313, 318, 319
Velocità media ... 271
Integrale indefinito ... 279
Venn ... 10
Integrali indefiniti immediati generalizzati ... 299
Weierstrass ... 193
Interi naturali ... 28
Zeri ... 194
335
Carlo Greco
Appunti di Analisi Matematica I
16. Indici
336
2. Indice dei teoremi
I numeri dopo la parola Teorema si riferiscono, rispettivamente, al Capitolo, alla Sezione e al numero del Teorema
all'interno della sezione. L'ultimo è il numero di pagina.
Teorema 1.2.1 HIrrazionalità di
2 L ... 8
Teorema 1.8.1 HPotenza dell'insieme delle partiL ... 21
Teorema 4.4.1 HRadici razionali 1L ... 72
Teorema 4.4.2 HRadici razionali 2L ... 73
Teorema 5.1.1 HProprietà di ax L ... 91
Teorema 5.1.2 HProprietà dei logaritmiL ... 94
Teorema 7.7.1 HUnicità del limiteL ... 152
Teorema 9.3.2 HOperazioni con le derivateL ... 207
Teorema 9.3.3 HDerivazione delle funzioni composteL ... 208
Teorema 9.7.1 HApprossimazione lineareL ... 214
Teorema 9.10.1 HRegola dell'HôpitalL ... 219
Teorema 10.1.1 HDi FermatL ... 225
Teorema 10.1.2 HRicerca del minimo e del massimo assolutoL ... 226
Teorema 10.1.3 HDi RolleL ... 227
Teorema 7.7.2 HOperazioni con i limitiL ... 154
Teorema 10.1.4 HDi LagrangeL ... 228
Teorema 7.7.4 HOperazioni con le funzioni continueL ... 158
Teorema 10.1.6 HTest per i punti di minimo o massimo relativoL ...
Teorema 7.7.5 HForma indeterminata b ê 0L ... 160
232
Teorema 7.9.1 HPermanenza del segno per i limitiL ... 166
Teorema 11.2.1 HIntegrabilità delle funzioni continueL ... 265
Teorema 7.7.3 HContinuità delle funzioni elementariL ... 158
Teorema 7.7.6 HLimite delle funzioni composteL ... 162
Teorema 10.1.5 HCriterio di monotoniaL ... 230
Teorema 10.3.1 HConvessità e concavitàL ... 236
Teorema 10.3.2 HDerivata a sinistra e a destraL ... 240
Teorema 7.9.2 HConservazione delle disuguaglianzeL ... 167
Teorema 11.2.2 HIntegrabilità delle funzioni monotoneL ... 265
Teorema 7.9.4 HConfronto per le funzioni 2L ... 169
Teorema 11.4.2 HDella mediaL ... 270
Teorema 7.9.3 HConfronto per le funzioni 1L ... 168
Teorema 7.11.1 HLimite delle successioni monotoneL ... 178
Teorema 7.11.2 HConfronto per le successioni 1L ... 178
Teorema 7.11.3 HConfronto per le successioni 2L ... 179
Teorema 7.11.4 HNumero di NeperoL ... 180
Teorema 11.4.1 HProprietà dell'integraleL ... 268
Teorema 11.6.1 HDifferenza di due primitiveL ... 273
Teorema 11.6.2 HFunzione integraleL ... 276
Teorema 11.6.3 HFondamentale del calcolo integraleL ... 277
Teorema 14.1.1 HConfronto per gli integrali impropriL ... 315
Teorema 7.11.5 HFunzione esponenzialeL ... 181
Teorema 14.1.2 HCriterio dell'infinitesimo per integrali impropriL ...
Teorema 8.1.1 HOperazioni con le funzioni continueL ... 186
316
Teorema 8.1.2 HPermanenza del segno per le funzioni continueL ...
321
189
321
Teorema 14.3.1 HCriterio di confronto per gli integrali impropriL ...
Teorema 14.3.2 HCriterio dell'infinito per gli integrali impropriL ...
Teorema 8.2.1 HDi WeierstrassL ... 193
Teorema 15.1.1 HFormula di Taylor per i polinomiL ... 325
Teorema 8.3.2 HDei valori intermediL ... 197
Teorema 15.1.3 HFormula di Taylor con il resto di PeanoL ... 327
Teorema 8.3.4 HIntersezione di graficiL ... 198
Teorema 15.3.2 HMinimi, massimi, flessiL ... 329
Teorema 8.3.1 HDegli zeriL ... 194
Teorema 8.3.3 HDi BolzanoL ... 197
Teorema 9.3.1 HContinuità delle funzioni derivabiliL ... 206
Settembre 2008
Teorema 15.1.2 HResto n-esimo della formula di TaylorL ... 326
Teorema 15.3.1 HTest della derivata n-esimaL ... 328
Teorema 15.4.1 HFormula di Taylor con il resto di LagrangeL ... 329
Carlo Greco
Appunti di Analisi Matematica I
337
16. Indici
3. Indice delle definizioni
I numeri dopo la parola Definizione si riferiscono, rispettivamente, al Capitolo, alla Sezione e al numero della Definizione
all'interno della sezione. L'ultimo è il numero di pagina.
Definizione 1.1.1 HInsiemi ugualiL ... 7
Definizione 7.1.1 HLimite con x0 œ , ed b œ L ... 138
Definizione 1.4.1 HUnione di insiemiL ... 10
Definizione 7.1.3 HLimite con x0 = ≤¶, ed b œ L ... 144
Definizione 1.1.2 HSottoinsieme di un insiemeL ... 7
Definizione 1.4.2 HIntersezione di insiemiL ... 10
Definizione 7.1.4 HLimite con x0 = ≤¶, ed b ≤¶L ... 146
Definizione 1.4.4 HProdotto cartesiano di insiemiL ... 11
Definizione 7.4.2 HLimite a destraL ... 149
Definizione 1.5.2 HGrafico di una funzione tra insiemiL ... 14
Definizione 7.7.1 HFunzione continuaL ... 157
Definizione 1.4.3 HComplementare di un insiemeL ... 10
Definizione 1.5.1 HFunzione tra insiemiL ... 12
Definizione 1.6.1 HCodominioL ... 14
Definizione 1.6.2 HFunzione surgettivaL ... 14
Definizione 1.6.3 HFunzione ingettivaL ... 15
Definizione 1.6.4 HFunzione inversaL ... 17
Definizione 1.6.5 HFunzione bigettivaL ... 17
Definizione 7.4.1 HLimite a sinistraL ... 148
Definizione 7.6.1 HDefinizione generale di limiteL ... 151
Definizione 7.11.1 HLimite di una successioneL ... 177
Definizione 8.1.1 HFunzione continuaL ... 186
Definizione 8.2.1 HMinimo e di massimo assolutoL ... 191
Definizione 9.1.1 HDerivataL ... 201
Definizione 9.2.1 HDerivata a sinistra o a destraL ... 203
Definizione 1.7.1 HFunzione compostaL ... 17
Definizione 9.2.2 HPunto angoloso o cuspidaleL ... 205
Definizione 1.8.1 HInsiemi equipotentiL ... 19
Definizione
Definizione 1.7.2 HRestrizione di una funzione tra insiemiL ... 19
Definizione 1.8.2 HInsieme infinitoL ... 19
Definizione 1.8.3 HInsiemi numerabiliL ... 20
Definizione 10.1.1 HPunto di minimo o massimo relativoL ... 224
HPunto di minimo o massimo relativo proprioL ... 224
Definizione 10.1.3 HPunto criticoL ... 225
Definizione 10.3.1 HFunzione convessa o concavaL ... 235
Definizione 1.8.4 HPotenza minoreL ... 21
Definizione 10.3.2 HPunto di flessoL ... 236
Definizione 3.1.1 HFunzione tra insiemi numericiL ... 37
Definizione 11.1.2 HPlurirettangoloL ... 258
Definizione 2.1.1 HInsiemi separatiL ... 30
Definizione 3.4.1 HFunzione pari o dispariL ... 47
Definizione 3.4.2 HFunzione periodicaL ... 48
Definizione 11.1.1 HRettangoloL ... 258
Definizione 11.1.3 HArea di un plurirettangoloL ... 258
Definizione 11.1.4 HInsieme misurabileL ... 259
Definizione 3.4.3 HPeriodo minimoL ... 49
Definizione 11.2.1 HTrapezoideL ... 259
51
Definizione 3.5.2 HCodominioL ... 52
Definizione 11.6.1 HPrimitiva o antiderivataL ... 273
Definizione 3.5.4 HFunzione ingettivaL ... 53
Definizione 13.1.1 HFunzione infinitesimaL ... 303
Definizione 3.5.1 HMinoranti, maggioranti, funzioni limitateL ...
Definizione 3.5.3 HFunzione surgettivaL ... 53
Definizione 11.2.2 HIntegrale secondo RiemannL ... 261
Definizione 11.6.2 HFunzione integraleL ... 273
Definizione 3.5.5 HFunzione inversaL ... 54
Definizione 13.1.2 HFunzione infinitesimaL ... 303
Definizione 3.7.2 HCrescenza e decrescenzaL ... 61
Definizione 13.2.1 HOrdine di infinitesimo 1L ... 306
Definizione 3.7.1 HStretta crescenza o decrescenzaL ... 60
Definizione 3.7.3 HMonotoniaL ... 61
Definizione 3.8.1 HSuccessioneL ... 62
Definizione 3.8.2 HMonotonia per le successioniL ... 63
Definizione 5.1.1 HEsponenzialeL ... 91
Definizione 5.1.2 HLogaritmoL ... 92
Definizione 5.2.1 HSeno e CosenoL ... 96
Definizione 5.2.2 HArcosenoL ... 98
Definizione 5.2.3 HArcocosenoL ... 100
Definizione 5.2.4 HTangenteL ... 102
Definizione 5.2.5 HArcotangenteL ... 104
Settembre 2008
Definizione 7.1.2 HLimite con x0 œ , ed b = ≤¶L. ... 143
Definizione 13.1.3 HConfronto tra infinitesimiL ... 303
Definizione 13.2.2 HOrdine di infinitesimo 2L ... 307
Definizione 13.3.1 HFunzioni infiniteL ... 308
Definizione 13.3.2 HFunzioni infiniteL ... 308
Definizione 13.3.3 HConfronto di infinitiL ... 309
Definizione 13.4.1 HOrdine di infinito 1L ... 309
Definizione 13.4.2 HOrdine di infinito 2L ... 309
Definizione 14.1.1 HIntegrale improprio in @a, + ¶@L ... 313
Definizione 14.2.1 HIntegrale improprio in L ... 318
Definizione 14.3.1 HIntegrale improprio in Da, bDL ... 319
Definizione 15.1.1 HPolinomio di TaylorL ... 325
10.1.2
Carlo Greco
Appunti di Analisi Matematica I
338
16. Indici
4. Notazioni
Segnaliamo le principali differenze tra le notazioni usate in queste dispense e quelle standard.
f @xD
Simbolo di funzione
f HxL
‰
Numero di Nepero
e
‰
Funzione esponenziale
ex
Log@xD
Logaritmi naturali
log x
Sin@xD
Funzione seno
sen x
Cos@xD
Funzione coseno
cos x
Tan@xD
Funzione tangente
tg x
ArcSin@xD
Funzione arcoseno
arcsen x
ArcCos@xD
Funzione arcocoseno
arccos x
ArcTan@xD
Funzione arcotangente
arctan x
Notazione usata nelle dispense
x
Sec@xD
Csc@xD
Funzione secante H
Notazione standard
1
L
cos x
Funzione cosecante H
1
L
sin x
Cot@xD
Funzione cotangente H
Sin@xD2
Seno al quadrato
Sin@x2 D
Settembre 2008
Significato
1
L
tg x
Seno di x al quadrato
sec x
cosec x
cotg x
sin2 x
sinHx2 L