1
ISTRUZIONI PER INIZIARE
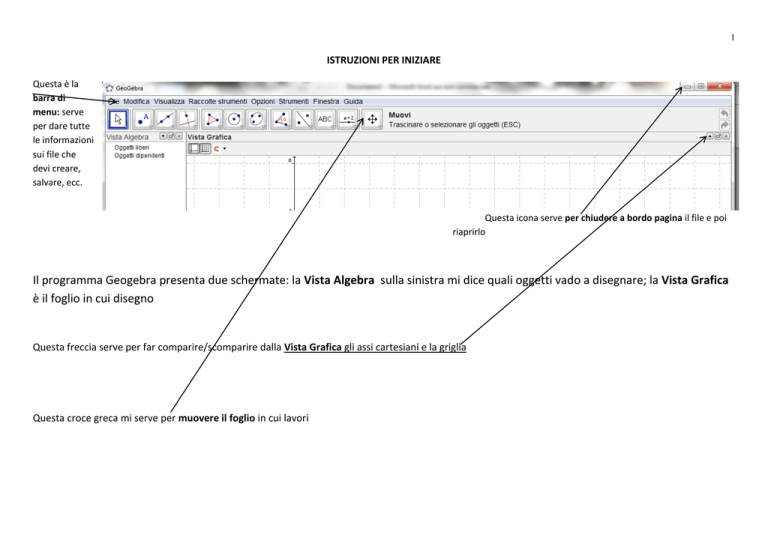
Questa è la
barra di
menu: serve
per dare tutte
le informazioni
sui file che
devi creare,
salvare, ecc.
Questa icona serve per chiudere a bordo pagina il file e poi
riaprirlo
Il programma Geogebra presenta due schermate: la Vista Algebra sulla sinistra mi dice quali oggetti vado a disegnare; la Vista Grafica
è il foglio in cui disegno
Questa freccia serve per far comparire/scomparire dalla Vista Grafica gli assi cartesiani e la griglia
Questa croce greca mi serve per muovere il foglio in cui lavori
2
Quando apri il programma Geogebra ti si presenta questa schermata:
Nome del programma
Simbolo del puntatore
Punto
E, più in basso, questa schermata:
Rispetto a Cabri, Geogebra presenta il vantaggio di avere già gli assi cartesiani e la griglia, per facilitare il disegno. Come spiegato
precedentemente, basta far comparire i due pulsanti Griglia e Assi Cartesiani, cliccando sulla freccetta in alto a destra.
3
COSTRUZIONE DI UN TRIANGOLO E PRIMA ISOMETRIA: LA TRASLAZIONE
Il quinto tasto da sinistra ti permette di disegnare un Poligono. Disegna il triangolo ABC di vertici: A = (3; 1) B = (6; 2) C = (2; 5)
Nella Vista Algebra compaiono le coordinate di ciascun punto:
Sempre nella Vista Algebra compare la lunghezza dei lati a, b, c del triangolo
Compare infine l’area del poligono: poli1=6,5
Per calcolare il perimetro del triangolo clicca sull’icona Distanza o lunghezza e poi
Poli1 della Vista Algebra
clicca sul
Clicca con il tasto destro del mouse sul punto A; ti comparirà questo menu a tendina:
Mostra oggetto ti consente di nascondere il punto e poi, se vuoi, cliccando
seconda volta, farlo ricomparire
Mostra etichetta ti permette di far scomparire e poi riapparire l’etichetta con il nome del punto.
Elimina, ovviamente elimina il punto A
Rinomina permette di cambiare il nome del punto (ricorda, sempre maiuscolo).
una
4
Il tasto Proprietà ti consente di fare molte funzioni. Quando clicchi su questo tasto si apre una
finestra come questa:
Togliendo la spunta, puoi:
Scegliere di non mostrare il punto;
Scegliere di mostrare l’etichetta con il valore (cioè le coordinate) del punto;
Cambiare il colore del punto (MENU COLORE)
Ora esercitati a disegnare 6 punti,
a colorarli in modo diverso,
a cambiare il loro aspetto,
a spostarli
a far comparire le loro coordinate cartesiane come nell’esempio
Ora disegna un vettore con la funzione Vettore tra due punti disegnando due punti che distano 4 unità con direzione orizzontale verso sinistra
(Ovest)
RICORDA: un vettore è un segmento orientato, di cui occorre definire la lunghezza (modulo), la direzione e il verso
Nella Vista Algebra compaiono le caratteristiche del vettore:
il primo valore in alto (-4) indica che la componente del movimento
lungo l’asse delle ascisse (cioè in orizzontale) vale 4 unità ed è preceduta dal
segno negativo, perché la direzione verso destra (Est) è considerata positiva e
quella verso Ovest è considerata negativa. Il numero 0 scritto più in basso
indica che la componente del movimento lungo l’asse delle ordinate è nulla,
infatti il movimento che facciamo compiere è solo in direzione orizzontale.
Aumenta lo spessore del vettore andando su Proprietà/Stile/Spessore
5
Ora clicca sull’icona delle isometrie e scegli Traslazione
Clicca sul triangolo per selezionare l’oggetto da traslare, poi clicca sul vettore per dire al computer qual è la
direzione, il verso e il modulo (la distanza) della traslazione.
Analizza le coordinate dei punti traslati e compila la seguente tabella:
PUNTI
A
B
C
ASCISSA
ORDINATA
PUNTI
A’
B’
C’
ASCISSA
ORDINATA
Le ordinate dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC?
Le ascisse dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC? Come?
Prova a completare le seguenti equazioni:
x’ =…………….
y’ = ………………… dove x’ e y’ sono, rispettivamente, le ascisse e le ordinate dei punti
A’, B’ e C’.
6
PUN
TI
A
B
C
Ora prova a spostare la direzione e il verso del vettore in modo che sia lungo 4 unità, con direzione verticale e verso Nord (Alto)
Compare questa schermata:
Il vettore u ha componente 0 lungo l’asse
e +4 lungo l’asse delle ordinate.
Compila ora la seguente tabella:
ASCIS
SA
ORDINA
TA
PUN
TI
A’
B’
C’
ASCIS
SA
delle ascisse
ORDINA
TA
Le ordinate dei punti A’B’C’ sono cambiate
quelle dei punti ABC?
Le ascisse dei punti A’B’C’ sono cambiate
quelle dei punti ABC? Come?
Prova a completare le seguenti equazioni:
x’ =…………….
y’ = ………………… dove x’ e y’ sono, rispettivamente, le ascisse e le ordinate dei punti A’, B’ e C’.
Prova infine a vedere cosa succede con un vettore obliquo
I triangoli ABC e A’B’C’ sono congruenti?....................................
Segui il verso per andare da A a B a C: segui un verso orario o antiorario?.......................
Segui il verso per andare da A a B a C: segui un verso orario o antiorario?........................
rispetto a
rispetto a
7
Le figure ABCD e A’B’C’D’ sono direttamente o inversamente congruenti?.................................
Collega con un segmento i punti corrispondenti A e A’
Collega con un segmento i punti corrispondenti B e B’
Collega con un segmento i punti corrispondenti C e C’
Come sono tra loro questi segmenti?............................................................................
Come sono questi segmenti rispetto al vettore?.......................................................................................................................
8
SIMMETRIA ASSIALE
o Con l’icona Triangoli costruisci un triangolo ABC di vertici: A= (3; 2) B = (7;2) C = (4;5)
o Clicca ora sull’icona Simmetria assiale e poi seleziona, cliccando, sul triangolo e poi sull’asse y. Ti compare il triangolo A’B’C’ simmetrico di ABC
rispetto all’asse delle ordinate.
o costruisci i segmenti AA', BB' e CC'
Come sono i segmenti AA’, BB’ e CC’ tra loro?
.................................................
Come sono i segmenti AA’, BB’ e CC’ rispetto all’asse di simmetria?.
................................................................
.
o Completa ora la seguente affermazione e scrivila in una
casella di testo: I segmenti che uniscono punti simmetrici rispetto ad
una retta sono..............................rispetto a tale retta
o trova il punto medio dei segmenti AA', BB', CC' con il comando Costruisci/Punto medio. Che cosa
noti?.................................................................
o Completa la seguente affermazione: e scrivila in una casella di testo: i punti simmetrici sono.........................dalla retta che costituisce l'asse di
simmetria.
9
o Prendi ora un punto qualunque sull’asse y e disegna con il comando Simmetria assiale il suo simmetrico rispetto alla retta a
o Che cosa noti?.................................................................
o Completa la seguente affermazione e scrivila in una casella di testo: ogni punto appartenente all'asse di simmetria ha come simmetrico
.............................., perciò tutti i punti sull'asse si dicono punti uniti.
o Seleziona il comando Puntatore, poi avvicinati ad un vertice del triangolo e spostalo. Che cosa succede al triangolo
A'B'C'?.............................................
o Completa: due figure corrispondenti in una simmetria assiale sono tra loro..........................
o Segui il verso per andare da A a B a C: segui un verso orario o antiorario?.......................
o Segui il verso per andare da A a B a C: segui un verso orario o antiorario?........................
o Le figure ABCD e A’B’C’D’ sono direttamente o inversamente congruenti?.................................
o Analizza le coordinate dei punti corrispondenti e compila la seguente tabella:
10
PUNTI
A
B
C
ASCISSA
ORDINATA
PUNTI
A’
B’
C’
ASCISSA
ORDINATA
o Le ordinate dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC?
o Le ascisse dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC? Come?
o Prova a completare le seguenti equazioni:
x’ =…………….
o y’ = ………………… dove x’ e y’ sono, rispettivamente, le ascisse e le ordinate dei punti A’, B’ e
C’.
ESEGUI ORA UNA SIMMETRIA ASSIALE CON ASSE x
o Analizza le coordinate dei punti corrispondenti e compila la seguente tabella:
PUNTI
A
B
C
ASCISSA
ORDINATA
PUNTI
A’
B’
C’
ASCISSA
ORDINATA
o Le ordinate dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC?
o Le ascisse dei punti A’B’C’ sono cambiate rispetto a quelle dei punti ABC? Come?
o Prova a completare le seguenti equazioni:
x’ =…………….
o
y’ = ………………… dove x’ e y’ sono, rispettivamente, le ascisse e le ordinate dei punti
A’, B’ e C’.
11
ROTAZIONE
o Costruisci uno Slider (cioè un cursore) con il comando
o Clicca in un punto qualsiasi dello schermo grafico e compare questa finestra:
12
o
o
o
o
Dato che noi dobbiamo lavorare con gli angoli, scegli l’opzione Angolo che chiamerai α;
Con il comando Poligono costruisci il quadrilatero di vertici: A = (2; 4) B = (1; 1) C = (3; 2)
D = (2; 2)
Premi il pulsante Punto/Intersezione di due oggetti, costruisci il punto di intersezione degli assi e chiamalo O;
Ora fai compiere una Rotazione
o Per eseguire la rotazione devi: selezionare il poligono ABCD,
tuo centro di rotazione, infine il computer ti chiede l’ampiezza
come ampiezza quella dell’angolo αmoltiplicata per 58 e il
poi selezionare il punto O che rappresenta il
dell’angolo di rotazione e il verso; tu scegli
verso antiorario come in figura:
o Adesso vai su Puntatore e sposta lo slider
o Fai compiere una rotazione di 90° con lo slider: cosa succede al quadrilatero
ABCD?.......................................................................................................................................................
o Costruisci un arco di centro O ed estremi B e B’
o Costruisci un arco di centro O ed estremi A ed A’: come sono gli archi?............................................
o ……………………………………………………………………………………………………………………………………………………….
13
o Segui il verso per andare da A a B a C a D: segui un verso orario o antiorario?.......................
o Segui il verso per andare da A a B a C a D: segui un verso orario o antiorario?........................
o Le figure ABCD e A’B’C’D’ sono direttamente o inversamente congruenti?.................................
o Ora fai compiere allo slider un angolo di 180°: come sono i due triangoli?.............................
o Questa particolare rotazione di 180° è una simmetria centrale
o Infine sposta lo slider per compiere una rotazione di 360°: come sono i due poligoni?....................
14
o Scrivi in una casella di testo la seguente affermazione, completandola: “La rotazione è un’……………………………………………………………………….nella
quale occorre fornire un…………………………….di rotazione, un angolo di ……………………………………….e un ……………………………………che può essere
orario o antiorario.”
o Ora prova a compiere una rotazione del poligono ABCD sempre con lo stesso angolo dato dallo slider moltiplicato per 58 e con verso
antiorario, ma con centro in B: cosa succede al poligono ABCD?












