VAN

Corporate finance 2e
Capitolo 4
Valore attuale e flussi di
cassa
1
Panoramica del capitolo
Valutazione: il caso uniperiodale
Valutazione: il caso multiperiodale
Periodi di capitalizzazione
Semplificazioni
Quanto vale un’impresa?
Valutazione uniperiodale: un esempio
Pedro sta cercando di vendere un appezzamento di terreno in
Andalusia. Ieri gli hanno offerto €10 000.
Stava per accettare la proposta quando un’altra persona gli
ha offerto €11 424, che gli verrebbero pagate tra un anno.
Pedro ha accertato che entrambi i potenziali clienti sono
onesti e solvibili, perciò non teme che le lo possano
raggirare.
Quale offerta dovrebbe scegliere?
Soluzione
VA = € 11 424/1.12 = €10 200
Investite €10 000 al tasso di interesse del 12% e dopo un anno
avrete €11 200
Rispetto a € 11 424, la seconda opzione è preferibile
In alternativa, attualizzate €11 424 al valore di oggi (Valore
attuale) e avrete € 10 200
Rispetto a € 10 000 oggi, la seconda opzione è preferibile
Entrambi gli approcci portano alla stessa decisione
Formula per la valutazione uniperiodale
VA = C1/(1 + r)
dove C1 è il cash flow alla data 1 e r è il tasso di
rendimento che richiede Pedro dalla vendita del suo
terreno. Si chiama anche tasso di attualizzazione
Valutazione: il caso multiperiodale
Valore futuro e
capitalizzazione
Il potere della
capitalizzazione
Valore futuro e
capitalizzazione
La formula
algebrica
Valore futuro e capitalizzazione
Supponete di depositare in banca €1 per un anno la tasso d’interesse
del 9%. Quanto varrà tra un anno?
€1 x (1 + r) = €1 x 1.09 = €1.09
Che cosa accade se lasciate quella somma sul conto per un altro anno?
€1 x (1 + r) x (1 + r) = €1 x (1 + r)2 = 1 + 2r + r2
€1 x (1.09) x (1.09) =€1 x (1.09)2 = €1 + €0.18 + €0.0081 = €1.1881
Formula mutiperiodale
Valore futuro di
un investimento:
VF = C0  (1 + r)T
Il potere della capitalizzazione
Interesse semplice
R = 8.47 %
Interesse composto
R = 8.47 %
Investite £1 per 208 anni
Interesse = £0.0847
Investite £1 per 208 anni
Valore dell’investimento dopo
Valore dell’investimento dopo 208 anni
208 anni:
FV = £1(1.0847)208
£1 + (208 x £0.0847)
= £22,100,655
= £1 + £17.62
= £18.62
C’è una bella differenza!
Valore attuale e attualizzazione
Valore attuale e attualizzazione:
PV 
Ct
(1  r )
T
Esempio 4.5: Attualizzazione multiperiodale
Il Sig. Bianchi riceverà €10 000 tra tre anni.
Il Sig. Bianchi può ottenere un interesse dell’8% sul proprio
investimento, perciò il tasso di attualizzazione appropriato è
l’8%. Qual è il valore attuale del suo cash flow ?
 1 
PV  €10, 000  

 1.08 
 €10, 000  .7938
 €7,938
3
Esempio 4.6: Trovare il tasso
Un cliente di Chaffkin GmbH vuole acquistare un
rimorchiatore oggi stesso. Anziché pagare subito, pagherà
€50 000 tra tre anni. A Chaffkin GmbH costruire
immediatamente il rimorchiatore costerà €38 610. I cash
flow di Chaffkin sono visualizzati nella Figura 4.9. A che
tasso di interesse Chaffkin GmbH non guadagna né perde
dalla vendita?
Esempio 4.6: Trovare il tasso
Il rapporto tra costo di costruzione (valore attuale) e prezzo di
vendita (valore futuro) è:
€38, 610
 0.7722
€50, 000
Il tasso di interesse che consente a €1 da ricevere tra tre anni
di avere un valore attuale di €0.7722 è il 9%. Perché?
Esempio 4.6: Trovare il tasso
Esempio 4.7: Valutazione del Cash Flow
Paul Draper ha vinto un concorso di parole incrociate e riceverà i
seguenti cash flow nei prossimi due anni:
Anno
1
2
Cash Flow
€2,000
€5,000
Draper può ottenere attualmente un tasso di interesse del 6% dal
suo conto corrente. Qual è il valore attuale dei cash flow?
Il valore attuale netto: la formula algebrica
C1
C2
CT
VAN
NPV  C0 


L

T
1  r (1+r ) 2
(1 + r )
T
  C0  
i=1
Ci
(1 + r )
i
Periodi di capitalizzazione
A volte l’interesse viene applicato più di una volta
nel corso dell’anno
Semestralmente
(2 volte
all’anno)
Trimestralmente
(4 volte
all’anno)
Mensilmente
(12 volte
all’anno)
Settimanalmente
(52 volte
All’anno)
Quotidianamente
Continuativamente
(365 volte all’anno)
Formula per capitalizzare gli
interessi più di una volta all’anno
Capitalizzando una somma m volte all’anno si ottiene a fine
anno un capitale di:
r

C0  1  
m

m
(4.6)
dove C0 è l’investimento iniziale e r è il tasso di interesse
annuo nominale.
Il tasso di interesse annuo nominale è il tasso di interesse
annuo al netto della capitalizzazione
Esempio 4.9: Tasso d’interesse
effettivo annuo
Quale sarà il capitale di Cristina a fine anno, se riceve un
interesse nominale annuo del 24% composto mensilmente
su un investimento di €1?
12
 .24 
12
€11 

€1

(1.02)

12 

 €1.2682
Il rendimento effettivo annuo è il 26.82%. Questo tasso di
rendimento annuo prende il nome di tasso annuo effettivo
(TAE) o rendimento annuo effettivo (RAE).
Grazie alla capitalizzazione, il tasso di interesse effettivo
annuo è superiore al tasso di interesse nominale del 24%.
Formula del tasso effettivo annuo
m
r 

1


1


m

Capitalizzazione pluriennale
r

FV  C0 1  
m

mT
Il tasso di interesse percentuale annuo
Molti finanziamenti comportano esborsi aggiuntivi
iniziali o finali per spese di gestione, amministrative,
ecc.
Nell’UE, tutti i mutui devono specificare il tasso di
interesse effettivo, che include tutti i costi e non solo
gli interessi
Questo tasso prende il nome di Tasso percentuale
annuo o APR (Annual Percentual Rate)
Esempio 4.12: TAEG o APR
Il prezzo di vendita dell’auto è di € 30 000.
Il tasso nominale dichiarato è “un tasso di interesse semplice
del 12% sul capitale finanziato in origine per tre anni,
pagabile in 36 rate mensili”.
La finanziaria addebita anche spese amministrative per € 250.
Che cosa significa?
Il finanziatore applicherà un interesse del 12% annuo sul
prestito originario di € 30 000 per tre anni.
Ogni anno, la quota interessi sarà € 3600 (12% di 30 000), per
un totale di €10 800 in tre anni.
Esempio 4.12: TAEG
Importo
originario
Interessi e
spese
Pagamento
mensile
• L’automobile costa € 30,000
• Il totale degli interessi è €10,800
• Le spese amministrative ammontano a € 250
• (30,000 + 10,800)/36 = €1,133.33
Esempio 4.12: TAEG
Qual è il TAEG di questo finanziamento?
Si ottiene così un tasso percentuale annuo del 24.13%!
Il finanziatore deve anche dichiarare la somma totale annua
versata alla fine del contratto: in questo caso è
€ 41 049.88, mentre il costo totale del finanziamento è € 11
049.88 (41 049.88 – 30 000).
Capitalizzazione in continuo
L’interesse viene
capitalizzato ad ogni
infinitesimo istante
FV = C0  erT
Esempio 4.14: Valore attuale con
la capitalizzazione continua
Avete vinto un concorso di parole incrociate, ma il premio di
€1000 vi sarà pagato tra quattro anni. Se il tasso di
interesse annuo composto in continuo è l’8%, qual è il
valore attuale di questa somma?
€1,000 
1
.084
e
1
 €1,000 
 €726.16
1.3771
Semplificazioni
Rendita
perpetua
Rendita
perpetua
crescente
Rendita
annua
Rendita
annua
crescente
Rendite perpetue e rendite annue
Rendita perpetua
• Un flusso costante di cash flow che non finisce mai
Rendita annua
• Un flusso costante di cash flow che dura un numero
prefissato di periodi
Formula della rendita perpetua
C
C
C
PV 



L
2
3
1  r (1  r )
(1  r )
C

r
Esempio 4.15: Rendite perpetue
Considerate una rendita perpetua che paga €100 all’anno. Se
il tasso di interesse di riferimento è l’8%, qual è il valore del
consol?
Supponete ora che il tasso di interesse scenda al 6%. Quale
sarebbe il valore del consol?
Rendita perpetua crescente
PV 
C
r g
Esempio: Rendite perpetue crescenti
Immaginate un condominio di appartamenti in affitto che
l’anno prossimo procurerà al proprietario dei cash flow al
netto delle spese di €100 000. Questi cash flow dovrebbero
aumentare del 5% all’anno. Il tasso di interese di
riferimento è l’11%. Qual è il valore attuale dei cash flow?
€100, 000
.11  .05
 €1, 666, 667
Alcune osservazioni importanti
sulle formule della rendita perpetua
Importante !
Il numeratore
Il tasso di
L’ipotesi sulla
attualizzazione disponibilità
e il tasso di
temporale dei
crescita
flussi di cassa
Formula della rendita annua
1
1

PV  C  
r r (1  r ) T 


Esempio 4.16: Valutazione del premio di una lotteria
Il Sig. Verdi ha appena vinto una lotteria che paga € 50 000
all’anno per vent’anni. Riceverà il primo pagamento tra un
anno. Gli organizzatori della lotteria l’hanno intitolata Il
Milionario perché €1000 000 = €50 000 x 20 anni. Se il
tasso di interesse è l’8%, qual è il valore effettivo del
premio?
Il valore futuro della formula di una rendita annua
T
1
(1

r
)

FV  C

 r

r
(1  r )T

C

r
 1

Esempio 4.17: Investimento per la pensione
Supponete di versare ogni anno € 3000 in un conto di
risparmio, che vi dà un interesse annuo del 6% al netto
delle imposte. Quanto avrete tra 30 anni, quando andrete in
pensione?
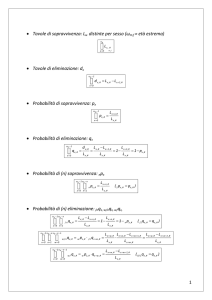
Formule per il calcolo della rendita annua
Aspetti problematici
Rendita
differita
Rendita
anticipata
Rendita
periodale
Equalizzare
il VA di due
rendite
Esempio: Rendita differita
Danielle Caravello riceverà una rendita annua di €500
all’anno, a partire dalla data 6. Se il tassi di interesse è il
10%, qual è il valore attuale della sua rendita? Come lo
calcolate?
1.Attualizzate la rendita riportandola all’anno 5
2. Attualizzate il valore della rendita dell’anno 5 riportandola
all’anno 0
Esempio 4.18: Rendite annue differite
Fase 1: Attualizzare la rendita all’anno 5
1 

1  (1.04) 4 
4
€500 
  €500  A.10
 .10 


 €500  3.1699
 €1, 584.95
Fase 2: Attualizzare la rendita dell’anno 5 all’anno 0
€1, 584.95
(1.10)
5
 €984.13
Esempio 4.21: Lavorare sulle
rendite annue
Antonio e Elena Rossi stanno risparmiando per pagare gli
studi universitari della foglia neonata Susanna. I coniugi
stimano che tra 18 anni, quando Susanna andrà
all’università, le spese universitarie ammonteranno a €30
000 all’anno. Nei prossimi decenni il tasso di interesse sarà
del 14%. Quanto devono depositare in banca ogni anno in
modo che le spese universitarie della figlia siano totalmente
coperte per tutti i quattro anni di università?
ESEMPIO 4.21: Equalizzare il
valore attuale di due rendite annue
Tre fasi:
1.Calcolare il valore delle spese universitarie all’anno 17
2.Calcolare il valore delle spese universitarie all’anno 0
3.Calcolare il cash flow che equalizza i versamenti effettuati
dall’anno 1 all’anno 17 al valore delle spese universitarie
all’anno 0
ESEMPIO 4.21: Equalizzare il
valore attuale di due rendite annue
1.
1 

1  (1.14)4 
4
  €30.000  A.14
€30, 000  
.14 



 €30, 000  2,9137  €87, 411
2.
€87, 411
 €9, 422.91
17
(1.14)
3.
C
A.17
14
 €9, 422.91
€9, 422.91
C
 €1, 478.59
6.3729
Rendita annua crescente
  1  g T 
1  


1 r  


PV  C

rg 




Esempio 4.22: Rendite annue crescenti
Gabriele, che frequenta il secondo anno dell’MBA, è stato
appena offerto un posto di lavoro da € 80 000 all’anno.
Prevede che il suo stipendio crescerà del 9% all’anno fino a
quando andrà in pensione, tra 40 anni. Se il tasso di
interesse è il 20%, qual è il valore attuale dei suoi introiti
complessivi da lavoro?
Esempio 4.22: Rendite annue crescenti
Applicate la formula della rendita annua crescente a €9422.91
e risolvete per C:
17 
  1  g T 

1.04 

1  

1  



1 r  
1.14  




C
C
 €9, 422.91

 .14  .04 
rg 








Qui, C = €1,192.78.