12 velocit ed accelerazione istantanee
annuncio pubblicitario
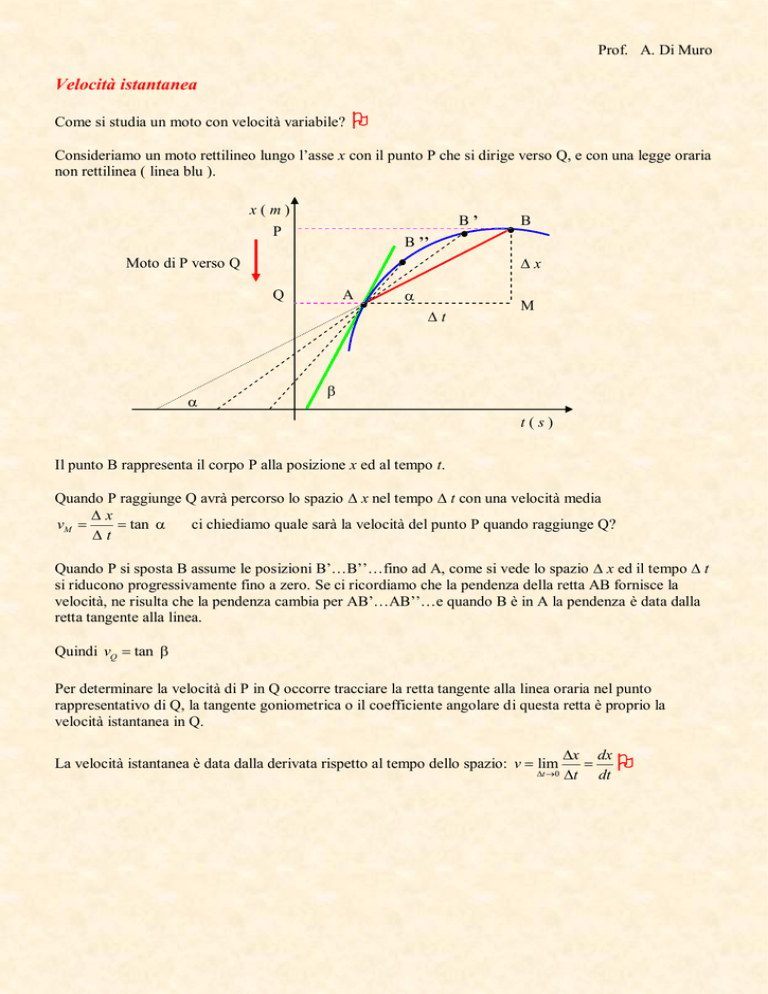
Prof. A. Di Muro Velocità istantanea Come si studia un moto con velocità variabile? Consideriamo un moto rettilineo lungo l’asse x con il punto P che si dirige verso Q, e con una legge oraria non rettilinea ( linea blu ). x(m) P B’ B ’’ Moto di P verso Q Q A B x t M t(s) Il punto B rappresenta il corpo P alla posizione x ed al tempo t. Quando P raggiunge Q avrà percorso lo spazio x nel tempo t con una velocità media x ci chiediamo quale sarà la velocità del punto P quando raggiunge Q? vM tan t Quando P si sposta B assume le posizioni B’…B’’…fino ad A, come si vede lo spazio x ed il tempo t si riducono progressivamente fino a zero. Se ci ricordiamo che la pendenza della retta AB fornisce la velocità, ne risulta che la pendenza cambia per AB’…AB’’…e quando B è in A la pendenza è data dalla retta tangente alla linea. Quindi vQ tan Per determinare la velocità di P in Q occorre tracciare la retta tangente alla linea oraria nel punto rappresentativo di Q, la tangente goniometrica o il coefficiente angolare di questa retta è proprio la velocità istantanea in Q. x dx t 0 t dt La velocità istantanea è data dalla derivata rispetto al tempo dello spazio: v lim Prof. A. Di Muro Accelerazione istantanea In modo del tutto analogo alla velocità istantanea, l’accelerazione istantanea in un punto P sarà il coefficiente angolare della retta tangente alla curva della legge oraria. L’accelerazione istantanea è data dalla derivata rispetto al tempo della velocità: a lim t 0 v dv t dt Come si trasporta il discorso sulla legge oraria della posizione? Se è la legge oraria della posizione, considerando un suo punto A, la retta tangente t e la sua perpendicolare n, detta normale, in A, esiste un cerchio detto cerchio osculatore, che approssima, nelle vicinanze ( intorno ) di A la curva . Il centro del cerchio osculatore sta sulla normale, il raggio R = A C 1 è detto raggio di curvatura di nel punto A, il suo reciproco 1 è la curvatura di in A. k R x(m) n t A C1 Il cerchio osculatore può stare o sotto o sopra la curva, se sta sotto diremo che la curva in A volge la concavità verso il basso, altrimenti volge la concavità verso l’alto. F O t(s) C2 B Se la velocità inizialmente positiva aumenta, aumenta anche la pendenza della legge oraria della posizione, in questo caso la velocità assume valori più grandi, il moto è accelerato con accelerazione positiva e, come si vede dalla fig. 1, la concavità è rivolta verso l’alto. Se invece la velocità inizialmente negativa diminuisce, il moto risulta sempre accelerato, ma l’accelerazione questa volta è negativa perché il suo segno deve essere concorde a quello della velocità e, come si vede dalla fig. 2, la concavità è rivolta verso il basso. v=4m/s v=3m/s v=2m/s v=1m/s Fig. 1 v=1m/s v=2m/s v=3m/s Fig. 2 v=4m/s Di conseguenza in tutti i punti in cui la curva volge la concavità verso l’alto si ha accelerazione positiva ed in tutti i punti in cui la curva volge la concavità verso il basso si ha accelerazione negativa. Il punto F è un punto di transizione tra le due concavità, in tale punto l’accelerazione cambia segno e quindi deve essere nulla. Il raggio di curvatura diventa infinito e la curvatura è nulla. Tale punto si chiama punto di flesso.
