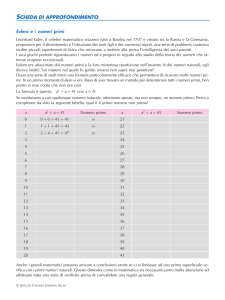
Note sui numeri complessi
Andrea Damiani
2 marzo 2015
Numero complesso
Definiamo, senza ulteriori considerazioni, unità immaginaria la
quantità
i=
√
−1
Definiamo poi il numero immaginario
z =a+ib
in cui a e b prendono il nome, rispettivamente di parte reale e
parte immaginaria di z:
a = Re(z)
b = Im(z)
L’insieme dei numeri complessi si indica con C.
Complesso coniugato
coniugato del numero complesso z = a + b i:
z = a−bi
cioè con la parte immaginaria cambiata di segno.
Ogni numero reale è coniugato di se stesso.
Il piano complesso (o piano di Argand, o di Gauss)
Piano cartesiano in cui l’asse delle ascisse è etichettato come asse
reale e l’asse delle ordinate come asse immaginario.
Se
z = a+bi
allora
Re(z) = a
Figura: Il piano complesso
Im(z) = b
Somma di numeri complessi
Si sommano separatamente le parti reali e le parti immaginarie:
(a + b i) + (c + d i) = (a + c) + (b + d) i
Sul piano complesso: somma di vettori.
Prodotto e quoziente di numeri complessi
Prodotto due numeri complessi z = a + b i e w = c + d i:
(a + b i)(c + d i) = (ac − bd) + (ad + bc) i
Quoziente di due numeri complessi:
a+bi
a+bi c −d i
(ac + bd) + (bc − ad) i
=
=
c +di
c +di c −di
c2 + d2
moltiplicando numeratore e denominatore per il coniugato del
denominatore.
Modulo di un numero complesso
Modulo (o norma) del numero complesso z = a + b i:
kzk = |z| =
√
zz =
p
a2 + b 2
Nel piano complesso, corrisponde alla lunghezza del vettore che
rappresenta z.
Forma polare dei numeri complessi
Rappresentazione in forma polare
z = a + b i = ρ (cos θ + i sin θ)
con
(
√
ρ = a2 + b 2
θ = arctan ba
e
(
a
b
= ρ cos θ
= ρ sin θ
Figura: La forma polare del numero
complesso
L’esponenziale complesso
Definizione: l’esponenziale complesso e z è la funzione y (z) che
risolve il problema di Cauchy:
(
y0 = y
y (0) = 1
La funzione esponenziale nel campo complesso ha le proprietà già
viste nei reali.
La formula di Eulero
Una relazione “sorprendente” fra la funzione esponenziale e le
funzioni goniometriche:
e iθ = cos θ + i sin θ
(Cotes 1714, Euler 1748).
Dimostrazione della formula di Eulero
Consideriamo
f (θ) = e iθ
e
g (θ) = cos θ + i sin θ
allora:
f (0) = 1
e f 0 (θ) = ie iθ = if (θ)
e inoltre
g (0) = 1
e
g 0 (θ) = − sin θ + i cos θ = ig (θ)
Quindi g (θ) risolve lo stesso problema di Cauchy di f (θ), per cui
f (θ) = g (θ) ∀θ ∈ R
Conseguenze della formula di Eulero
Ponendo θ = π nella formula di Eulero, e iπ = cos π + i sin π, cioè
e iπ + 1 = 0
che è definita da molti la formula più bella della Matematica.
Conseguenze della formula di Eulero
Il modulo di e iθ è 1. Due dimostrazioni fra le molte possibili:
Dim.1: approfittando del fatto che il
coniugato di e iθ è e −iθ :
√
|e iθ | = e iθ e −iθ =
√
√
= e iθ−iθ = e 0 = 1
Dim.2: calcolando direttamente il
modulo:
|e iθ | = | cos θ + i sin θ| =
2
2
= cos θ + sin θ = 1
Figura: Il modulo
dell’esponenziale complesso
Conseguenze della formula di Eulero
Forma polare del numero complesso:
z = ρ (cos θ + i sin θ)
si scrive ora cosı̀:
z = ρe iθ
con ρ = |z| e θ = Arg (z). Quindi per il prodotto di z1 = ρ1 e iθ1 e
z2 = ρ2 e iθ2 troviamo
z1 z2 = ρ1 ρ2 e i(θ1 +θ2 )
in pratica: si moltiplicano i moduli e si sommano le fasi.
Conseguenze della formula di Eulero
e i(α+β) = e iα e iβ =
= (cos α + i sin α)(cos β + i sin β) =
= (cos α cos β − sin α sin β) + i(sin α cos β + cos α sin β)
ma anche
e i(α+β) = cos(α + β) + i sin(α + β)
e quindi, eguagliando parti reali e parti immaginarie, troviamo le
formule di addizione
cos(α + β) = cos α cos β − sin α sin β
sin(α + β) = sin α cos β + cos α sin β
Conseguenze della formula di Eulero
Sussistono le importanti relazioni:
cos x =
e ix + e −ix
2
sin x =
e ix − e −ix
2i
e
Inoltre
e z = e x+iy = e x e iy = e x (cos y + i sin y )
che si dimostrano tutte per sostituzione diretta.
La potenza in C: la formula di De Moivre
Da
z = ρe iθ
segue
n
z n = ρn e iθ = ρn e niθ
quindi (formula di De Moivre, sicuramente già nota a Newton nel
1676):
z n = ρn (cos nθ + i sin nθ)
Teorema fondamentale dell’Algebra e radici dell’unità
In C, ogni polinomio di grado n ha esattamente n radici (Gauss*
1800, Argand 1806). * Sia la prima dimostrazione di Gauss (la sua tesi di dottorato) che la seconda
presentavano un errore.
L’equazione x n − 1 = 0 ha esattamente n radici complesse, date da
rk = cos
2πk
2πk
+ i sin
= e 2πik/n
n
n
• dimostrazione: dalla formula
di Eulero.
• sul piano di Gauss: la prima
radice è 1, le altre ai vertici
del poligono regolare di n
lati con centro nell’origine.