SISTEMI LINEARI
Premessa
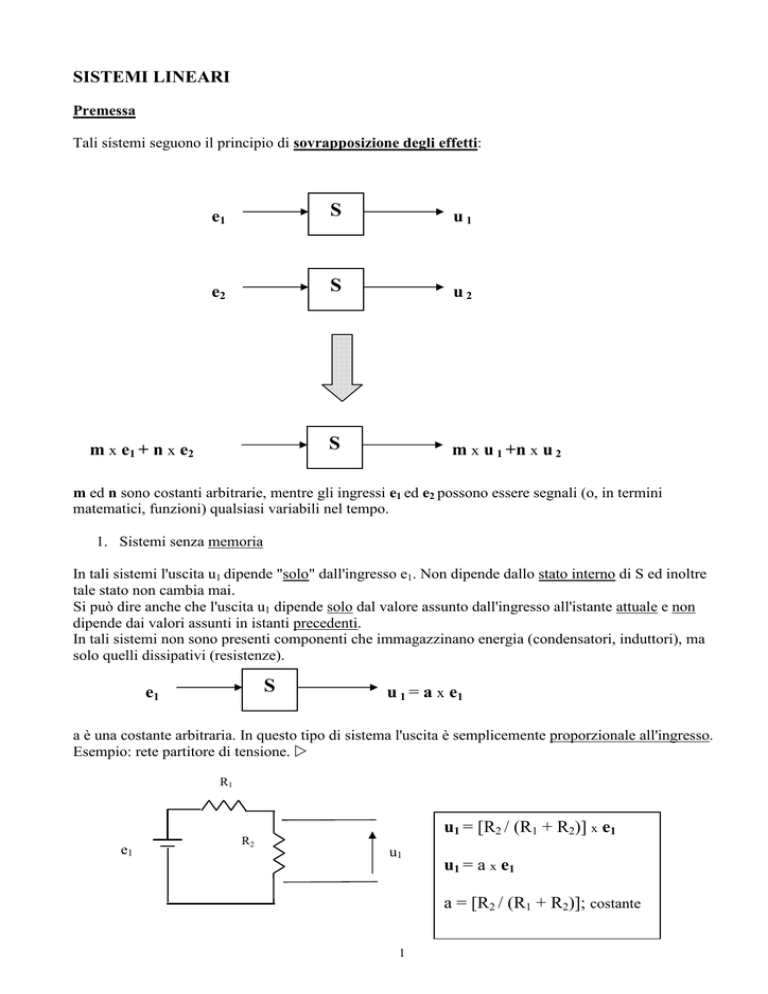
Tali sistemi seguono il principio di sovrapposizione degli effetti:
e1
S
u1
e2
S
u2
S
m x u 1 +n x u 2
m x e1 + n x e2
m ed n sono costanti arbitrarie, mentre gli ingressi e1 ed e2 possono essere segnali (o, in termini
matematici, funzioni) qualsiasi variabili nel tempo.
1. Sistemi senza memoria
In tali sistemi l'uscita u1 dipende "solo" dall'ingresso e1. Non dipende dallo stato interno di S ed inoltre
tale stato non cambia mai.
Si può dire anche che l'uscita u1 dipende solo dal valore assunto dall'ingresso all'istante attuale e non
dipende dai valori assunti in istanti precedenti.
In tali sistemi non sono presenti componenti che immagazzinano energia (condensatori, induttori), ma
solo quelli dissipativi (resistenze).
S
e1
u 1 = a x e1
a è una costante arbitraria. In questo tipo di sistema l'uscita è semplicemente proporzionale all'ingresso.
Esempio: rete partitore di tensione. R1
u1 = [R2 / (R1 + R2)] x e1
e1
R2
u1
u1 = a x e1
a = [R2 / (R1 + R2)]; costante
1
2. Sistemi con memoria
Tali sistemi presentano uno "stato" interno che può cambiare nel tempo.
Negli esempi che seguono lo stato interno suddetto è la tensione sul condensatore VC ( t0 ), prima che
l'ingresso e1 venga collegato. È noto dall'elettrotecnica che un condensatore può essere caricato ad una
tensione qualsiasi (entro i limiti massimi ammessi dalla tensione di rottura) indipendentemente dal
generatore e1 del circuito al quale deve essere collegato.
Esempio n° 1: condensatore scarico all'istante t0 di chiusura dell'interruttore I.
Ciò significa che VC ( t0 ) = 0 (stato interno zero).
Siccome devono sempre valere le leggi di Kirchoff alla maglia, allora all'istante t0 si può
scrivere anche:
e1 (t0) = VC ( t0 ) + u1 (t0)
e1 (t0) =
0 + u1 (t0)
e1 (t0) = u1 (t0) ;
quindi si ha: u1 (t0) = e1 (t0).
Esempio n° 2: condensatore carico all'istante t0 di chiusura dell'interruttore I.
VC = 0
R
e1
u1
I
Ciò significa che VC ( t0 ) = E (stato diverso da zero).
Siccome devono sempre valere le leggi di Kirchoff alla maglia, allora all'istante t0 si può
scrivere anche:
e1 (t0) = VC ( t0 ) + u1 (t0)
e1 (t0) =
E + u1 (t0)
u1 (t0) = e1 (t0) - E
VC = E
0
R
e1
u1
I
È evidente che l'uscita u1, ad un certo istante t0, non è determinato solo dall'ingresso e1, ma anche dallo
stato di S (cioè dalla situazione del condensatore, che può essere carico oppure scarico, e quindi dal
valore VC ( t0 )). Si può concludere dicendo che in tali sistemi sono presenti componenti che
immagazzinano energia (condensatori, induttori), oltre a quelli dissipativi (resistenze).
I sistemi senza memoria si definiscono anche sistemi di ordine zero. I sistemi con memoria si
definiscono anche sistemi di ordine 1, 2, ecc. Tali definizioni saranno chiarite al termine dei prossimi
paragrafi. 2
3. Sistemi di ordine zero.
Dal punto di vista dell'interpretazione fisica, questi sistemi non presentano elementi che immagazzinano
energia (per esempio nei circuiti elettrici non sono presenti i condensatori e gli induttori, ma soltanto
resistenze).
Verifichiamo la proprietà della linearità.
Applichiamo allo stesso circuito (partitore di tensione) prima l'ingresso Vi1, successivamente l'altro
ingresso Vi2, infine applichiamo la somma dei due generatori, cioè Vi1 + Vi2. Verificheremo il risultato
fornito dalle uscite.
R1
Vu1 = Vi1 [R2 / (R1 + R2)]
R2
Vi1
Vu1= a x Vi1
Vu1
a = [R2 / (R1 + R2)]; costante
R1
Vu2 = Vi2 [R2 / (R1 + R2)]
Vi2
R2
Vu2= a x Vi2
Vu2
a = [R2 / (R1 + R2)]; costante
Ora applichiamo come ingresso la somma dei due generatori, quindi li inseriamo in serie.
R1
Vu = (Vi1 +Vi2 )[R2 / (R1 + R2)]
Vi1
R2
Vu = a x Vi1 + a x Vi2
Vu
Vu = Vu1 + Vu2
Vi2
Il risultato Vu ci conferma quanto affermato riguardo ai sistemi lineari: se l'ingresso Vi1 produce l'uscita
Vu1 e l'ingresso Vi2 produce l'uscita Vu2, allora quando in ingresso è applicata la somma degli ingressi
singoli (Vi1 + Vi2 ), anche l'uscita risulterà la somma delle singole uscite Vu = Vu1 + Vu2.
Dalle relazioni scritte risulta chiaro che l'uscita del sistema di ordine zero, dipende solo dal valore attuale
dell'ingresso. In altri termini nelle relazioni scritte non interessa quanto valeva l'ingresso prima dell'istante
attuale, cioè non interessano i valori passati dell'ingresso. Ciò che conta è solo il valore assunto all'istante
attuale. Questa osservazione ci spiega il perché tali sistemi si chiamano anche senza memoria, poiché non
ricordano i valori assunti in passato dall'ingresso. 3
4. Sistemi del 1° ordine.
Dal punto di vista dell'interpretazione fisica, questi sistemi presentano un solo tipo di elemento che
immagazzina energia (per esempio nei circuiti elettrici sono presenti solo i condensatori o solo gli
induttori, oltre ad eventuali resistenze). Siccome tali sistemi presentano o condensatori o induttori (non
contemporaneamente!), per i quali non è noto lo stato interno (cioè se sono carichi o scarichi) all'istante
in cui si applica l'ingresso, occorre studiarne il comportamento in assenza dell'ingresso (con ingresso
zero) ed successivamente in presenza dell’ingresso.
Poniamo come ingresso un generatore di corrente costante a partire da un istante iniziale.
La forma di tale corrente fornita dal generatore ha la forma sotto riportata.
I
I0
t
Questo tipo di segnale che vale zero per t < 0 ed è costante, di valore I0, per t > 0, prende il nome di
GRADINO.
All'istante iniziale t = 0 − il condensatore è carico alla tensione V0 e non è collegato alla resistenza R in
modo che non possa scaricarsi e nemmeno al generatore di corrente (interruttore K su A) in modo che
non possa neanche caricarsi. All'istante t = 0 + si commuta l'interruttore K dalla posizione A a quella B
e si collega anche il condensatore C alla resistenza R. In questo unico istante di tempo, t = 0 + ,la
tensione V0 non cambia subito, mentre la resistenza assume una tensione iniziale VR (0+) = V0.
B
I
K
VR (t)
A
C
VC = VR = V0
+
istante t = 0
V0
K
VR(t)
A
(interr. K su B)
R
C
L’espressione della risposta V(t) ai capi del parallelo R e C è data dalla seguente espressione
matematica:
V (t ) = (V 0 − R ⋅ I ) ⋅ e− RC ⋅t
1
risp. transitoria
-
istante t = 0
(interr. K su A)
R
B
I
VC = V0
V0
+
R⋅I
risp. permanente
4
Il primo termine transitorio è destinato ad estinguersi (cioè ad annullarsi al passare del tempo), mentre
il secondo termine permanente è quello che dipende dall'ingresso I e quindi predominerà nel tempo.
Il comportamento del circuito si piega tenendo presente che il condensatore non si lascia attraversare
dalla corrente continua I, che pertanto scorrerà soltanto nella resistenza R. Come conseguenza la
tensione sulla resistenza ha il valore che si ottiene con la legge di Ohm: R*I. Tuttavia il condensatore è
già carico alla tensione V0 ed ha un valore qualsiasi (cioè può essere maggiore, minore o anche uguale
alla tensione sulla resistenza R*I). Siccome il condensatore e la resistenza sono collegati in parallelo le
tensioni su entrambi i componenti devono essere uguali. La conseguenza di tale situazione è che la
tensione sul condensatore non può rimanere uguale a V0 ma deve diventare uguale a quella presente
sulla resistenza, che è fissata dal generatore I. Da quanto detto si ricava che esisterà un intervallo di
tempo iniziale in cui la tensione V0 sul condensatore cambierà per assumere il valore R*I fissato dal
generatore. E’ chiaro che se V0 è maggiore di R*I il condensatore si dovrà scaricare, se V0 è minore di
R*I il condensatore si dovrà caricare, se V0 = R*I il condensatore non farà niente. Il periodo di tempo
occorrente al condensatore per raggiungere il valore corretto di tensione R*I si chiama regime
transitorio, il periodo di tempo successivo si chiama invece regime permanente.
Nella formula scritta la risposta transitoria dipende dal prodotto R*C.
♦ RC = τ = costante di tempo [sec]
♦ S0 = - 1/ RC = - 1 / τ = frequenza naturale [sec-1 ] = [Hertz]
Il numero "e" che compare nella formula è la costante di Nepero. Esso è un numero irrazionale e vale:
e = 2,718281…….
La costante di tempo τ = R*C non è il tempo che impiega il condensatore per raggiungere la giusta
tensione R*I. Infatti affinché si estingua il regime transitorio occorrono almeno 5 intervalli di tempo
pari a τ = R*C. Concludendo si può affermare che il tempo occorrente all’estinzione del regime
transitorio è pari a 5* τ . Questa affermazione ci fa capire che il transitorio dura di più se è grande τ
quindi se sono grandi sia R che C. Infine una considerazione importante è la seguente: il generatore,
cioè l’ingresso, non ha alcuna importanza nel transitorio, che dipende unicamente da R e da C, cioè
dipende unicamente da come è costruito internamente il circuito.
La grandezza S0 è denominata frequenza naturale ed è l’inverso di τ. Essendo l’inverso di un tempo è
una frequenza e quindi si misura in hertz. Il termine “naturale” significa che dipende unicamente da
come è costruito internamente il circuito e quindi dai valori di R e C.
Consideriamo adesso i grafici relativi alla formula appena scritta, facendo l’ipotesi che la tensione
iniziale V0 sia di valore maggiore della tensione finale R*I.
2,5
Vc
RISPOSTA COMPLETA = risposta permanente + risposta transitoria
V0
2,0
RI
1,5
risposta permanente
1,0
V0 - RI
risposta transitoria
0,5
0,0
0
1
2
3
5
4
5
t
6
5. Sistemi del 2° ordine.
Questi sistemi presentano due tipi di elementi che immagazzinano energia (per esempio nei circuiti
elettrici sono presenti sia i condensatori che gli induttori, oltre ad eventuali resistenze).
ESEMPIO:
Un sistema del secondo ordine può essere studiato sia con un esempio elettrico (circuito RLC), sia con un
iL (t)=0
VC
++ + +
VR
C
iR (t)=0
L
-- --
R
sistema meccanico (pendolo). In entrambi i sistemi vi sono due forme di energia che si trasformano
continuamente una nell'altra.
Supponiamo che inizialmente sia carico solo il condensatore (non l'induttore), ed inoltre la resistenza sia
scollegata, per cui l'energia non può dissiparsi.
Nel circuito in figura troviamo il condensatore inizialmente carico con l'energia elettrica [½*C*(VC)2]
dipendente dalla tensione VC che si stabilisce ai capi del condensatore. Nel pendolo, la situazione
precedente, equivale ad avere una massa m legata tamite una cordicella ad un punto fisso P, che è
posizionata ad una altezza h (punto A) rispetto al punto più basso dell'oscillazione (punto B), e quindi
possiede l'energia potenziale mgh.
E' noto che l'energia di un condensatore è di tipo statica poiché dipende dalla tensione (o potenziale
elettrico ) ma non dalla corrente, che anzi può anche non esserci. Ciò significa che anche l'energia di un
condensatore è una energia potenziale, così come la massa che si trova ad una altezza h dal terreno o
rispetto ad un altro punto qualsiasi (conta solo la differenza!).
Non appena le cariche possono muoversi (istante t= 0+) per costituire la corrente IC, esse troveranno un
P
m
C
A
h
B
unico percorso attraverso l'induttore L, poiché la resistenza è scollegata. Di conseguenza la corrente IL
permetterà all'induttore L di caricarsi di energia magnetica [½*L*(IL)2] dipendente solo dalla corrente IL.
Tale energia dipende cioè da cariche in movimento (la corrente) e pertanto in questa fase si sta
trasformando l'energia elettrica (potenziale) del condensatore in energia magnetica (cinetica)
dell'induttore. E' anche evidente che le cariche che abbandonano una delle armature del condensatore e
costituiscono una corrente, arriveranno sull'altra armatura e si neutralizzeranno con un numero uguale di
cariche ma di segno opposto. Quindi si giungerà dopo un certo intervallo di tempo in una nuova
situazione: condensatore scarico ed induttore percorso da una corrente massima.
6
Nell'esempio del pendolo ciò equivale a lasciare libero di oscillare la massa m e quindi di trasformare
l'energia potenziale in cinetica. Tutta l'energia potenziale si sarà trasformata in energia cinetica
[½*m*(v)2] solo nel punto B, dove quindi si avrà anche la massima velocità v della massa m. Da tale
paragone risulta quindi chiaro che nell'induttore si avrà la massima corrente quando è massima l'energia
magnetica, cioè quando il condensatore è completamente scarico.
Naturalmente il processo di trasformazione di energia non termina, quindi dopo un altro uguale intervallo
di tempo il pendolo si troverà nella posizione C, che corrisponde ad una ricarica del condensatore con le
polarità delle armature invertite, quindi ad una scarica dell'induttore che vedrà di nuovo azzerare la sua
corrente. In questa posizione l'energia è diventata di nuovo potenziale (elettrica) a scapito di quella
cinetica (magnetica).
Il fenomeno continua all'infinito con le stesse modalità già descritte, poiché ora il pendolo riprenderà ad
oscillare in verso opposto (da C verso B e poi A), ed il condensatore riprenderà a scaricarsi in verso
opposto ( la corrente si inverte) con la conseguenza che l'induttore si ricaricherà ma in verso opposto.
Graficamente si possono riportare la tensione su C e la corrente in L che risulteranno sinusoidi sfasate di
90°.
tensione su C e corrente in L
Vc e IL
1,5
istante t=T/4: L carico
pendolo in B
istante t=0: C carico;
pendolo in A
IL
1
Vc
istante t=T/4: C scarico
pendolo in B
0,5
t
0
0
-0,5
1
2
3
4
5
6
7
istante t=T
8
istante t=0: L scarico
pendolo in C
istante t=3T/4: C scarico;
pendolo in B
istante t=3T/4: L carico;
pendolo in B
-1
istante t=T/2: L scarico;
pendolo in C
istante t=T/2: C carico;
pendolo in C
-1,5
Concludendo questa discussione, resta da considerare solamente le conseguenze della presenza della
resistenza. La presenza di R nel sistema circuito RLC equivale alla presenza degli attriti nel sistema
pendolo. Tali attriti si possono attribuire al fissaggio della cordicella nel punto P e alla presenza dell'aria
attorno alla massa m. Le conseguenze nel pendolo sono intuitive: in un tempo più o meno lungo le
oscillazioni termineranno ed il pendolo si fermerà nel punto B. Nel circuito avverrà un cosa analoga
poiché l'energia immagazzinata nel condensatore e nell’induttanza diminuirà nel tempo poiché la
resistenza ne consuma continuamente una parte. Ora sorge il problema di capire come la resistenza
consuma l’energia immagazzinata. Si possono verificare due situazioni differenti:
a) la resistenza consuma l’energia immagazzinata molto rapidamente;
b) la resistenza consuma l’energia immagazzinata molto lentamente;
7
9
Nel caso a) la resistenza consuma l’energia immagazzinata in L e in C più rapidamente di quanto questi
elementi riescano a scambiarsela. Nell’esempio del pendolo significa che la massa m è immersa in un
fluido viscoso (es.: olio denso). Quindi la massa m parte dal punto A e termina la sua corsa nel punto B
senza superarlo, cioè senza oscillazioni. Ciò avviene perché l’energia potenziale della massa m viene
dissipata o consumata nell’attrito con il fluido viscoso, senza dare il tempo alla massa di superare il punto
B. Questo caso si può paragonare ad un circuito RLC parallelo con una resistenza molto piccola. In
1 L
l’energia si consuma o si attenua senza effettuare
particolare se vale la relazione R < ⋅
2 C
iC (t)
iL (t)
iR (t)
VR
VL
VC
L
C
VC(0) = V0
IL(0) = I0
R
oscillazioni.
1,2
iL
1,0190524
1,0
0,8
0,6
0,4
0,2
t
0,0
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
Di seguito è visualizzata la curva che rappresenta la corrente IL nell’induttanza L
Nel caso b) la resistenza consuma l’energia immagazzinata in L e in C più lentamente di quanto questi
elementi riescano a scambiarsela. Nell’esempio del pendolo significa che la massa m è immersa in un
fluido poco viscoso (es.: aria). Quindi la massa m parte dal punto A e la sua corsa supera il punto B lo
supera, arriva in un punto C’ meno alto di C, inverte il verso di oscillazione supera di nuovo B,
arriva in un punto A’ meno alto di A, e ricomincia l’oscillazione. E’ evidente che il moto della massa
m terminerà nel punto B dopo diverse oscillazioni. Ciò avviene perché l’energia potenziale della massa m
viene dissipata o consumata nell’attrito con l’aria molto lentamente, quindi la massa avrà la possibilità di
superare più volte il punto B, quindi di oscillare. Questo caso si può paragonare ad un circuito RLC
1 L
parallelo con una resistenza sufficientemente grande. In particolare se vale la relazione R > ⋅
2 C
l’energia si consuma o si attenua con moto oscillatorio.
Di seguito è visualizzata la curva rappresentativa della corrente IL nell’induttanza L.
8
1.5
iL
1
0.5
0
0
0.5
1
1.5
2
2.5
3
t
-0.5
-1
-1.5
Da questo secondo caso risulta chiaro che in un sistema del 2° ordine possono coesistere due fenomeni:
quello della dissipazione dell’energia attraverso una resistenza o attrito e quello dell’oscillazione dovuto
al continuo scambio di energia tra condensatore ed induttanza. Questi due fenomeni sono studiati tramite
due parametri sotto riportati per il caso di un circuito RLC.
α = costante di smorzamento ( inversamente proporzionale ad R)
ω 0 = frequenza di risonanza (non dipende da R)
La costante di smorzamento tiene conto della dissipazione tramite la resistenza mentre la frequenza di
risonanza indica con quale velocità (cioè quante volte al secondo) L e C si scambiano l’energia in assenza
di dissipazione.
CONCLUSIONI :
Le risposte studiate dipendono da α (costante di smorzamento) ed ω0 (pulsazione di risonanza). Se
prevale l'effetto dello smorzamento (cioè R è abbastanza piccola, e quindi α abbastanza grande), la
risposta ( in questo caso iL) non oscilla, ma si estingue secondo un andamento esponenziale [caso a) ].
Se invece l'effetto dello smorzamento è meno importante dell'effetto di immagazzinamento dell'energia
(quindi R è abbastanza grande, pertanto i due elementi C ed L hanno il tempo per scambiare energia),
la risposta si estinguerà, però con andamento sinusoidale smorzato [caso b)]. Infine se non esiste
smorzamento (cioè R = ∞ ), non esistono cioè perdite, allora prevale l'effetto della risonanza (ω0) e
quindi l'uscita è sinusoidale non smorzata (l'ampiezza non varia).
9
1,70
iL 1,60
x=0,293
y=1,543
1,50
Fascia
d'errore di
±10%
1,40
1,30
sovraelongazione
1,20
1,10
1,00
0,90
x=0,14371
y=0,9
0,80
Tempo di assestamento
0,70
0,60
0,50
0,40
x=0,092525
y=0,5
x=0,03
y=0,1
0,30
Valore finale = 1
Tempo di salita
0,20
0,10
0,00
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
1,10
1,20
1,30
1,40
1,50
t 1,60
I parametri importanti della forma d'onda indicati in figura sono così definiti:
Tempo di salita: tempo impiegato dalla forma d'onda per passare dallo 10% allo 90% del valore finale.
Tale tempo si può valutare guardando in figura le coordinate dell'asse del tempo in corrispondenza dei
valori dell'ordinata 0,1 e 0,9. Si ottiene che: τS =0,14371 - 0,03 ≈ 0,1137. L'unità di misura del tempo
dipende dall'applicazione concreta.
Tempo di ritardo: tempo impiegato dalla forma d'onda per passare dal valore 0 allo 50% del valore
finale. Anche ora tale tempo si può valutare guardando in figura le coordinate dell'asse del tempo in
corrispondenza dei valori dell'ordinata 0 e 0,5. Si ottiene che: τR ≈ 0,0925.
Sovraelongazione: ampiezza del picco al di sopra del valore finale. In questo caso vale 1,543.
Tempo di assestamento: tempo impiegato dalla risposta per assestarsi entro ±10% del valore finale ( la
percentuale del 10% può variare a seconda delle applicazioni, per esempio = 0,1%). In questo caso tS =
1,0125.
10












