Marketing e matematica delle popolazioni

La matematica delle popolazioni a servizio del marketing
Peculiarità e limiti dei modelli di diffusione di prodotti e tecnologie
Lo sviluppo e il lancio di un nuovo prodotto o servizio sul mercato è sempre un rischio: analisi
e studi approfonditi e simulazioni scrupolose, dinanzi al giudizio inappellabile del cliente,
possono infatti rivelarsi fallimentari. L’imponderabile è sempre in agguato: l’idea può non
destare interesse, giungere in ritardo o in anticipo rispetto alle aspettative del cliente, che,
quindi in questi casi, può rivelarsi addirittura un concorrente inaspettato.
Tuttavia, se il prodotto o il servizio si impone, al Direttore Marketing si pongono nuovi problemi
legati alla gestione del successo. Quale può essere la sua massima diffusione? A che punto
intervenire con campagne pubblicitarie a supporto dell’offerta? Quando provvedere ad un suo
eventuale restyling? Come reagire all’ingresso di un eventuale concorrente nella nicchia di
mercato? Domande sintetizzabili in un concetto che sta alla base delle teorie di marketing: il
ciclo di vita di un prodotto.
Per sviluppare stime attendibili è possibile adottare strumenti già definiti nel campo della
matematica delle popolazioni e dell’epidemiologia. Il modello più semplice è anche il più antico,
ossia quello di Malthus.
Si consideri un prodotto, formulando una serie di ipotesi restrittive:
• mancanza di concorrenti, e quindi di possibili scelte da parte del cliente;
• bacino di utenza isolato, ossia la propensione all’acquisto è indipendente da stimoli
esterni, come ad esempio l’andamento economico e la pubblicità;
• comportamento omogeneo del cliente, in cui sono trascurabili differenze strutturali quali
età, sesso, distribuzione geografica;
• comportamento del cliente invariante nel tempo:il tasso di acquisto e di abbandono di
un prodotto può ritenersi costante.
Malthus ha sintetizzato queste ipotesi in una semplice equazione differenziale che lega la
variabile tasso di acquisto (il numero medio di prodotti acquisiti per cliente) con il tasso di
abbandono (il numero medio di prodotti abbandonati per cliente) che può essere pari a 0.
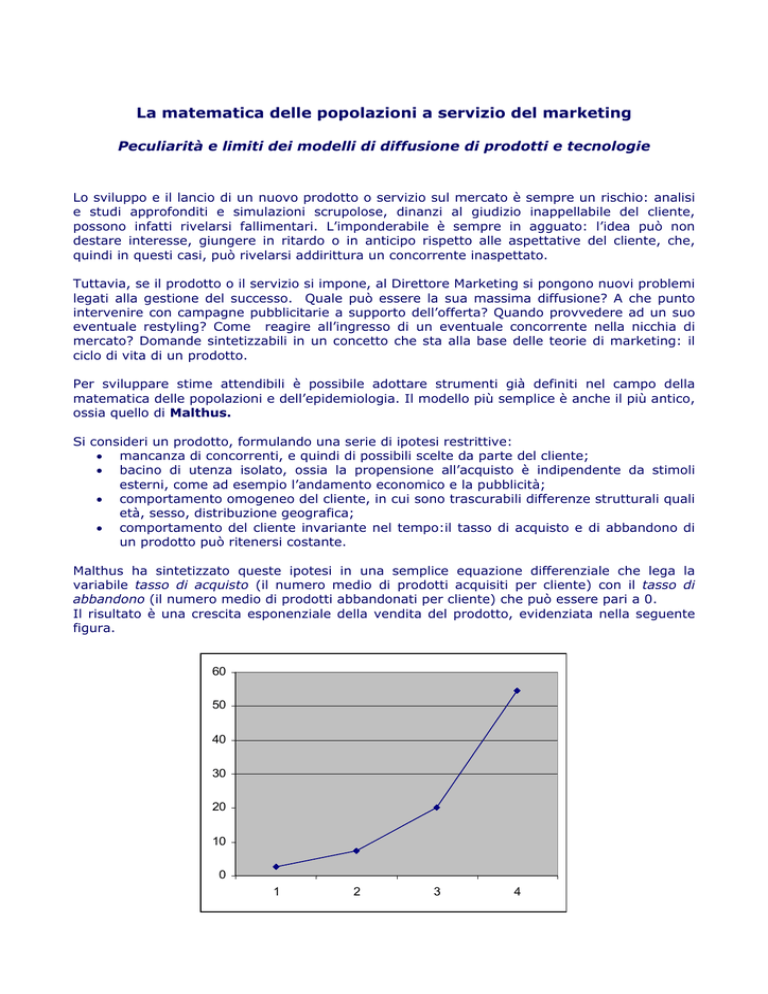
Il risultato è una crescita esponenziale della vendita del prodotto, evidenziata nella seguente
figura.
60
50
40
30
20
10
0
1
2
3
4
Figura 1: Andamento Esponenziale
Tale andamento rappresenta il sogno di ogni Responsabile Marketing. Ma, ahimé, la realtà non
è mai così idilliaca poiché sussiste un problema insormontabile costituito dal fatto che il
numero dei potenziali clienti è sempre finito.
Il passo successivo è quindi quello di raffinare il modello, utilizzando un concetto legato al
buon senso, così sintetizzabile: l’incremento della diffusione di un prodotto causa la
diminuzione del suo tasso di acquisto e un aumento del suo tasso di abbandono.
Risolvendo le varie equazioni matematiche che sono alla base di tale teoria si ottiene la
cosiddetta funzione logistica, il cui andamento è mostrato nella Figura 2.
Figura 2: Funzione Logistica
Indipendentemente dalla condizione iniziale di mercato, a regime, la penetrazione del prodotto
si stabilizzerà sul valore K. Ciò ha delle conseguenze, in ambito marketing, immediate:
• il massimo dello sforzo pubblicitario deve essere fatto in fase di lancio e al termine
dell’andamento lineare, in modo da allontanare il più possibile l’istante in cui il tasso di
penetrazione si avvicini a K;
• la differenziazione dell’offerta può avvenire durante la fase di crescita “lineare” della
diffusione del prodotto;
• quando il gap tra K e la funzione logistica è minore di un valore stabilito a priori dal
marketing, il ciclo di vita del prodotto si può considerare concluso.
Alcuni studi Key Partners hanno dimostrato che è possibile rendere tale modello più realistico
facendo riferimento all’epidemologia, ossia ai modelli matematici che descrivono il contagio di
una malattia.
Si proceda a suddividere l’insieme dei potenziali clienti K in due classi, variabili nel tempo:
coloro che hanno comprato il prodotto I(t) e coloro che non lo hanno comprato S(t).
Si formulino, in aggiunta a quanto descritto in procedenza, due nuove ipotesi:
- un’evoluzione del mercato basata sull’eventualità che chi ha comprato il prodotto possa
disfarsene, ridiventando un potenziale cliente;
- la constatazione che alla diffusione del prodotto non contribuisca soltanto la pubblicità,
ma anche il fenomeno del passaparola (dal punto di vista matematico, la percentuale di
incontri nell’unità di tempo che causano un nuovo acquisto).
Il risultato è la funzione evidenziata nel grafico successivo:
Figura 3: Funzione epidemologica
Il nuovo andamento, a prima vista molto simile a quanto visto per la funzione logistica, riporta,
in realtà, una differenza: esiste infatti una seconda soglia il cui valore è dipendente sia dalla
percentuale di clienti che comprano più volte un prodotto, sia dal tasso di diffusione tramite
interazioni tra clienti, il passaparola.
Al di sotto del valore di tale soglia la diffusione del prodotto tende rapidamente a 0 (il che
implica il suo fallimento) mentre al di sopra si riscontra un comportamento analogo a quanto
descritto in precedenza.
Ma la realtà, ribadiamolo, è molto più complessa della teoria. Nello studio della demografia, si
è visto come K non sia stabile, ma vari nel tempo. Ciò dipende da cambiamenti esogeni,
mutazioni dell’ambiente, ed endogeni, legati alla crescita stessa della popolazione, come il
consumo delle risorse disponibili o le energie spese per la socializzazione.
Stesso discorso per il Mercato: il tasso di penetrazione di un prodotto è legato sia agli
andamenti macroeconomici (in tempo di crisi la propensione all’acquisto e la disponibilità
economica sono minori) sia al mutare degli stili di vita e della cultura del potenziale cliente.
Inoltre, come nella realtà biologia bisogna tener conto dell’insorgenza di eventuali mutazioni,
nelle simulazioni di vendita, dato che il rapporto tra cliente e fornitore è di tipo retroattivo e
quindi non lineare, è necessario considerare anche gli effetti di comportamenti caotici. Per
tener conto di tale fenomeno è necessario l’utilizzo di equazioni derivate da modelli ON/OFF.
L’ultimo esempio di applicazione dei modelli demografici si trova proprio nello studio della
concorrenza. Consideriamo due prodotti che occupano la stessa “Nicchia ecologica”, ossia
che soddisfino lo stesso bisogno, che si rivolgono al medesimo target di clientela e che siano
perfettamente succedanei.
Ipotizziamo che l’uno in assenza dell’altro possano evolvere secondo la funzione logistica e che
il tasso di penetrazione di ciascun prodotto diminuisca all’aumentare di quello del concorrente.
Il tutto è sintetizzabile in un sistema di equazioni che, una volta eseguito, porta alla soluzione
evidenziata nel seguente grafico.
Figura 4: Soluzione Modello concorrenza
Tale soluzione conferma quanto dichiarato dal buon senso:
due prodotti distinti a regime non possono occupare la medesima nicchia ecologica ma
necessariamente uno dei due si estingue mentre l’altro tende a saturare il mercato.
Concludendo, i modelli matematici, per quanto affascinanti, sono strumenti e non fini, possono
cioè confermare deduzioni empiriche oltre che fornire idee e spunti di riflessioni. In
quest’ottica, tutte le Teorie possono rivelarsi passibili di perfezionamento o addirittura specchio
distorto e semplificato del Reale.
Può perciò supportare la decisione, ma non sostituirsi a quel misto di intuito, coraggio,
esperienza e rapidità di decisione che costituisce la forza di ogni manager e che in periodi di
vacche magre rappresenta realisticamente quel quid distintivo che permette ad
un’organizzazione di vincere la sfida di una competizione sempre più agguerrita.
Alessio Brugnoli
Business Analyst Key Partners