MINUENDO - SOTTRAENDO = DIFFERENZA

MATEMATICA
LEZIONE 6
DIFFERENZA DI NUMERI RELATIVI
(Prof. Daniele Baldissin)
ARGOMENTI
1) Significato di somma algebrica
2) Regole per effettuare la somma algebrica
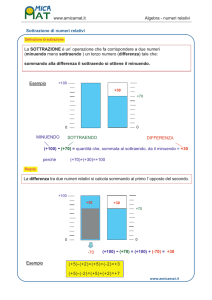
Come sappiamo dall'aritmetica, la sottrazione è l’operazione che consente di associare due numeri,
detti rispettivamente minuendo e sottraendo, ad un terzo numero (se esso esiste) detto differenza
o resto, tale che addizionato al sottraendo dia come risultato il minuendo.
Ovvero
MINUENDO - SOTTRAENDO = DIFFERENZA.
Quindi la differenza tra due numeri relativi, presi in un dato ordine, è un terzo numero che
aggiunto al secondo dà per somma il primo.
Inoltre, possiamo dire che la differenza di due numeri relativi esiste sempre e si ottiene
aggiungendo al primo l'opposto del secondo.
Mentre nell'aritmetica (ovvero nell'ambito dei numeri naturali) la differenza tra due numeri è
possibile solamente se il minuendo è maggiore, o tutt'al più uguale, al sottraendo, nell'ambito dei
numeri relativi, la sottrazione può essere sempre eseguita anche se il minuendo è inferiore rispetto
al sottraendo.
Ammissibile solo se
Minuendo > sottraendo
Numeri naturali
Minuendo = sottraendo
Minuendo > sottraendo
Numeri relativi
Minuendo = sottraendo
Minuendo < sottraendo
Numeri naturali. Esempi:
10 - 2 = 8
10 - 10 = 0
Numeri relativi. Esempi:
(+10) - (+2) = (+10) + (-2) = +8
(-10) - (-10) = (-10) + (+10) = 0
(-10) - (+5) = (-10) + (-5) = -15 - minuendo < sottraendo.
Poiché la sottrazione di due numeri relativi non è altro che l'addizione tra il primo numero e
l'opposto del secondo, essa viene ricondotta ad una somma. Per questa ragione, nell'ambito dei
numeri relativi, addizione e sottrazione costituiscono una sola operazione detta somma algebrica.
SOMMA DI NUMERI
RELATIVI
DIFFERENZA DI
NUMERI RELATIVI
SOMMA ALGEBRICA
di
NUMERI RELATIVI
Pertanto, possiamo definire la somma algebrica come un insieme di numeri relativi legati fra loro
da segni di addizione e sottrazione.
SOMMA ALGEBRICA: INSIEME DI NUMERI RELATIVI LEGATI TRA
LORO DA SEGNI DI ADDIZIONE E SOTTRAZIONE.
Esempio:
(+2) - (+5) + (-2) - (-4).
Date le regole relative alla somma e alla sottrazione di numeri relativi, essa può essere scritta come:
(+2) + (-5) + (-2) + (+4).
In questo modo ci troviamo di fronte ad una somma di numeri relativi.
Per semplicità, si è convenuto di scrivere la somma di numeri relativi senza le parentesi,
scrivendo i numeri uno appresso all'altro, ciascuno con il proprio segno. In pratica si sopprime il
segno + che indica l'operazione di addizione.
Quindi possiamo scrivere:
+2 -5 -2 +4.
Inoltre, quando il primo addendo di una somma è positivo il suo segno (che sarà +) può essere
tralasciato.
Quindi, possiamo anche scrivere:
2 -5 -2 +4.
Attenzione!! Il segno del primo addendo non può essere tralasciato se esso è negativo.
Esempio:
-5 + 4 + 3.
I numeri che compongono una somma algebrica si dicono termini della somma. I termini di una
somma vanno presi con i rispettivi segni.
NUMERI CHE COMPONGONO LA SOMMA
ALGEBRICA
TERMINI DELLA
SOMMA
presi con il loro segno
+2
Esempio:
-5
2 -5 -2 +4
-2
+4
Per eseguire la somma algebrica, occorre ricordare due importanti regole.
1° REGOLA.
Quando davanti ad una parentesi che racchiude una somma algebrica, vi è il segno +, si può togliere
la parentesi sopprimendo il segno + che la precede e lasciando inalterati i segni dei suoi addendi.
Esempio:
2 + (-5 + 3).
Eseguiamo:
2 + (-5 + 4) = 2 + (-1) = +1.
Ora osserviamo che otteniamo lo stesso risultato se togliamo la parentesi sopprimendo il segno +
che la precede e scrivendo i termini al suo interno ognuno con il proprio segno. Ovvero:
2 - 5 + 4 = +1.
Quindi, quando davanti ad una parentesi che racchiude una somma vi è un segno +, si può
togliere la parentesi e lasciare inalterati i segni dei suoi addendi.
Esempio:
-5 + (+4 - 3) = -5 + 4 - 3 = -4.
2° REGOLA.
Se vogliamo sottrarre ad un numero una somma, dobbiamo aggiungere al numero l'opposto di
quella somma. Ma l'opposto di una somma si ottiene cambiando di segno a tutti gli addendi.
Esempio:
+ 8 - (-3 + 2).
Eseguiamo:
+ 8 - (-3 + 2) = +8 - (-1) = +8 + (+1) = +9.
Ora osserviamo che otteniamo lo stesso risultato se cambiamo di segno a tutti gli addendi tra
parentesi. Ovvero:
+ 8 - (-3 + 2) = +8 + (+3 - 2) = +8 + (+1) = + 9.
Quindi, quando davanti ad una parentesi che racchiude una somma vi è un segno -, si può
togliere la parentesi e cambiare il segno a tutti gli addendi della somma.
Esempio:
- 12 - (5 -3 +7) = -12 -5 +3 - 7 = -21
Ricapitolando:
SI TOGLIE LA PARENTESI
E SI LASCIANO GLI
PARENTESI CHE
ADDENDI DELLA SOMMA
RACCHIUDE UNA SOMMA OGNUNO CON IL PROPRIO
PRECEDUTA DAL SEGNO +
SEGNO
4 + (-2 + 1) = 4 -2 + 1 = 3
SI TOGLIE LA PARENTESI
E SI CAMBIANO I SEGNI
PARENTESI CHE
DEGLI ADDENDI DELLA
RACCHIUDE UNA SOMMA
SOMMA
PRECEDUTA DAL SEGNO 4 - (-2 + 1) = 4 +2 - 1 = 5