ADDIZIONE
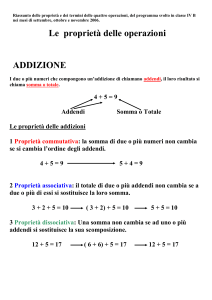
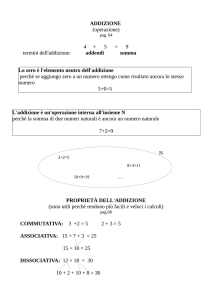
I termini dell’addizione si chiamano addendi e il risultato dell’addizione è detto somma.
Come si ottiene la somma? Aggiungendo al primo numero tante unità quante ne indica il secondo numero.
Ad esempio: consideriamo
3 + 5. Come calcolo il risultato? Parto da 3 aggiungo 5 unità. Ottengo così 8
che è il risultato dell’addizione.
3 e 5 sono addendi, mentre 8 è la somma.
Se ad un qualsiasi numero aggiungiamo 0 otteniamo sempre lo stesso numero iniziale. Cioè in
simboli possiamo scrivere:
+ = ∀ ∈ .
Si dice che 0 (zero) è
neutro dell’addizione. Neutro perché il risultato non cambia.
L’addizione è un’operazione interna all’insieme N. Infatti
l’elemento
sommando due numeri naturali
ottengo sempre un numero naturale. Si può anche dire che N è chiuso rispetto all’addizione.
PROPRIETA’ DELL’ADDIZIONE
COMMUTATIVA
Scambiando l’ordine degli addendi il risultato non cambia.
Ad esempio:
3 + 6 = 96 + 3 = 9
In simboli posso scrivere: + = + ∀, ∈ ASSOCIATIVA
La somma di tre o più addendi non cambia se a due o più di essi si sostituisce la loro somma.
Ad esempio posso considerare 13 + 6 + 4. Posso prima sommare 6 + 4 (=10) e poi fare
13 + 10 = 23. E’ utile per fare i calcoli a mente perché mi consente di sommare prima i numeri più
“semplici” da sommare.
DISSOCIATIVA
La somma di due o più addendi non cambia se a uno o più di essi si sostituiscono altri addendi
aventi per somma l’addendo sostituito.
Sembra difficile, in realtà anche in questo caso è utile per i calcoli a mente.
Ad esempio: 13 + 27. E’ più facile e immediato fare 13 + 7 + 20 oppure sommare prima le decine e
poi le unità. Si può fare così solo perché c’è la proprietà dissociativa. Pensaci, in realtà ti viene
automatico!
SOTTRAZIONE
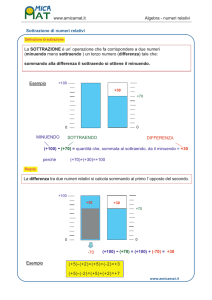
La sottrazione è l’operazione che associa a due numeri, detti minuendo e sottraendo, un terzo numero
chiamato differenza che addizionato al secondo dà il primo. Il minuendo deve essere maggiore o uguale al
sottraendo,
Esempio:
− = differenza
Minuendo sottraendo
Perché 11 – 3 = 7? Perché 7 + 3 = 11.
Infatti la sottrazione è l’operazione inversa dell’addizione. La prova della sottrazione è l’addizione cioè per
verificare se ho svolto correttamente la sottrazione devo sommare il risultato con il sottraendo e devo
ottenere il minuendo.
Se la sottrazione è corretta:
differenza + sottraendo = minuendo.
Se due numeri sono uguali la loro differenza è 0 (zero). Ad esempio: 5 – 5 = 0.
In generale − = ∀ ∈ La differenza tra un numero e lo zero è uguale al numero stesso. Ad esempio: 9 – 0 = 9.
In generale
− = ∀ ∈ Abbiamo detto che il minuendo deve essere maggiore o uguale al sottraendo, quindi la sottrazione NON è
un’operazione interna all’insieme N. Infatti NON è vero che se prendo due qualsiasi numeri naturali la loro
sottrazione è un numero naturale. Ad esempio 5 – 12 non si può fare nell’insieme dei numeri naturali.
PROPRIETA’ DELLA SOTTRAZIONE
INVARIANTIVA
Aggiungendo o togliendo uno stesso numero al minuendo e al sottraendo, la differenza non
cambia.
Ad esempio: 32 − 13 = 19. Aggiungiamo sia al minuendo che al sottraendo ad esempio 7 e
otteniamo 32 + 7 − 13 + 7 = 39 − 20. Adesso la sottrazione è più semplice e il risultato è 19.
Oppure partendo sempre dalla sottrazione iniziale posso togliere 2 ad entrambi i membri e ottengo
32 − 2 − 13 − 2 = 30 − 11. Anche in questo caso il calcolo è più semplice e ottengo sempre
19.
Vediamo quindi che anche questa proprietà è utile per il calcolo mentale o veloce.