Complementary stuff chapter 3

4
MACCHINA IN CORRENTE CONTINUA
4.1
Struttura e schema elementare
Per comprendere il principio di funzionamento della macchina in corrente continua (m.c.c.)
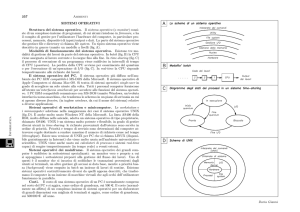
facciamo riferimento alla struttura elementare indicata in Fig. 4.1.
d
d
θr
A
1
φe
2
B
a
Fig. 4.1 - Struttura elementare del motore in corrente
continua
Fig. 4.2 - Percorso del flusso di eccitazione
Lo statore è del tipo a poli salienti. Sui poli sono avvolte le bobine che compongono
l’avvolgimento di campo o di eccitazione. Tale avvolgimento è percorso da corrente continua e
genera il flusso di eccitazione (o di campo) del motore, indicato con φe. Questo flusso è di tipo
stazionario, cioè la sua configurazione spaziale (mappa) resta fissa nel tempo. Indichiamo con d
l’asse magnetico (fisso) del flusso di eccitazione.
Sul rotore, cilindrico, immaginiamo disposta una sola spira (avvolgimento elementare) le cui
estremità 1 e 2 fanno capo a due lamelle, tra loro isolate e solidali al rotore (cioè ruotano assieme
alla spira). Le lamelle sono in contatto elettrico con due spazzole (indicate con A e B), che sono
invece solidali con lo statore e tenute in pressione sulle lamelle mediante molle.
Le spazzole permettono di accedere elettricamente, dal riferimento fisso di statore,
all’avvolgimento disposto sul rotore (qui composta dall’unica spira) detto avvolgimento di
armatura.
Indichiamo con a l’asse magnetico dell’avvolgimento di armatura, coincidente con l’asse
della spira 1-2 e fissiamo di misurare l’angolo di rotazione θr tra l’asse d e la direzione negativa
dell’asse a.
Lo schema della macchina in corrente continua è indicato nella seguente Fig. 4.3.
Visto in termini di sistema di conversione elettromeccanico la macchina in corrente continua
possiede due porte elettriche (gli avvolgimenti di eccitazione e di armatura) attraverso le quali
transita potenza elettrica (in termini di prodotto tensione–corrente ai morsetti) ed una porta
Cap.4 MCC struttura (2001) 31/03/01 11.47
50
Cap. 4 Macchina in corrente continua
meccanica (l’asse di rotazione) attraverso la quale transita potenza meccanica in termini di
prodotto velocità di rotazione–coppia.
In base ai versi di tali flussi di potenza si può avere il funzionamento da generatore oppure da
motore come illustrato nel seguito. Concordemente alle convenzioni utilizzate nella scrittura
dell’equazione dell’equilibrio dinamico e nella definizione del piano coppia–velocità
considereremo positive le potenze nel funzionamento da motore, cioè potenza elettrica entrante e
potenza meccanica uscente (coppia e velocità concordi).
eccitazione
armatura
asse di rotazione
Fig. 4.3 - Schema elementare della macchina in corrente continua
4.2
4.2.1
Principio di funzionamento
Funzionamento da generatore
In questo tipo di funzionamento viene fornita potenza elettrica (Pe) all’avvolgimento di
eccitazione e potenza meccanica (Pm) all’asse di rotazione, e si raccoglie potenza elettrica (Pa)
sull’avvolgimento di armatura. La macchina in corrente continua si comporta da generatore (o
dinamo) e può essere utilizzato per alimentare un carico (indicato in figura dalla resistenza Rc).
Per fissare le idee, consideriamo la struttura elementare del m.c.c. nella quale un motore
primo metta (dall’esterno) in rotazione il rotore (ad es. nel verso crescente di ϑr) mentre si
alimenta l’eccitazione con un generatore in continua.
4.2.1.1 Funzionamento da generatore a vuoto
Analizziamo dapprima il caso in cui l’avvolgimento di armatura sia aperto (ia = 0) cioè il
funzionamento da generatore a vuoto1, Fig. 4.4.
La spira di rotore concatena una parte del flusso generato dall’eccitazione. A seguito della
rotazione il flusso concatenato con la spira varia e si genera una tensione indotta che in base alla
Legge di Faraday scritta con la convenzione dell’utilizzatore (C.d.U) fornisce:
1
Rispetto la figura, se si trascurano le perdite per attrito e ventilazione, nel funzionamento da generatore a vuoto si avrà, a regime,
C = Pm = 0.
Principio di funzionamento
51
ie
+
Pe
ia = 0
ve
ea
Pa = 0
Rc
C,ω
Pm
Fig. 4.4 - Funzionamento da generatore a vuoto
ea ≡ eAB
Ea
2π
π
φ̂
θr
e12
φ
Fig. 4.5 - Tensione indotta nella spira elementare
e 12 =
dφ
dt
(4.1)
Il flusso concatenato sarà massimo negativo per θr = 0, nullo per θr = π/2. Ipotizzando un
andamento sinusoidale si può scrivere:
ˆ cos θ
φ = −φ
r
(4.2)
ˆ dθr sinθ = φ
ˆ ω sinθ
e 12 (θr ) = φ
r
r
dt
(4.3)
da cui:
ie
+
Pe
ia
ve
Pm
va
C,ω
Pa
Rc
52
Cap. 4 Macchina in corrente continua
Fig. 4.6 - Funzionamento da generatore a carico
Se chiamiamo eAB la tensione raccolta sulle spazzole, in base alla rotazione del rotore si
hanno le seguenti situazioni di contatto2:
-
in θr ∈(0,π) si hanno i contatti:
A≡1, B≡2, da cui: eAB = e12
-
in θr ∈(π,2π) i contatti si invertono:
A≡2, B≡1, da cui: eAB = e21 = −e12.
La tensione raccolta tra le spazzole rappresenta la tensione indotta nell’avvolgimento di
armatura (ea ≡ eAB), il cui andamento, riportato nella figura precedente, è quindi di tipo continuo,
nel senso di unipolare a valor medio (Ea) non nullo, Fig. 4.5.
Si osserva pertanto come, con il sistema collettore a lamelle + spazzole si realizza un
commutatore in grado di trasformare una alternata in una continua.
Intuitivamente, estendendo il numero di spire è possibile ottenere tensioni più continue,
praticamente costanti, come accade nei motori reali.
4.2.1.2 Funzionamento da generatore a carico
Vediamo ora cosa succede nel funzionamento a carico (Fig. 4.6), quando cioè viene chiuso
l’interruttore e quindi fluisce una corrente ia nell’avvolgimento di armatura.
d
C
C
φe
φe
φa
A
1(+)
va
B
φa
A
ia
2(+)
ia
Rc
va
Rc
1(-)
2(-)
ω
a
d
θr ∈(0,π)
B
ω
a
θr ∈( π,2π)
Fig. 4.7 - Generazione del flusso di armatura nel funzionamento da generatore
Con riferimento alla Fig. 4.7, in base al segno della tensione indotta si ha che per θr ∈(0,π)
l’estremo 1 ha potenziale maggiore dell’estremo 2, pertanto nel circuito esterno di carico la
corrente fluisce da 1 (punta della freccia) verso 2 (coda della freccia)3. Per effetto di questa
corrente si genera un flusso di armatura diretto in verso opposto all’asse di magnetizzazione (a).
Per θr ∈(π,2π) la situazione si inverte, cioè 2 ha potenziale maggiore di 1, ma il verso delle
correnti è lo stesso e quindi anche la direzione del flusso di armatura.
2
Si trascurano le posizioni limite 0,π e 2π.
Concordemente alla convenzione del generatore (C.d.G.) nell’avvolgimento di armatura la corrente fluisce dal morsetto a
potenziale minore verso quello a potenziale maggiore.
3
Principio di funzionamento
53
d
φe
φa
ω
Fig. 4.8 - Flussi di eccitazione e di armatura con una sola spira di armatura
In sostanza, il flusso di armatura è diretto sempre nel semipiano di destra della figura, è
allineato e concorde con il flusso di eccitazione per θr = 0 e θr = 2π, allineato e discorde per θr = π
e non allineato nelle rimanenti posizioni. La successiva Fig. 4.8 illustra questo aspetto, mettendo
in luce come, al ruotare della spira, il verso della corrente sia sempre uscente per il conduttore
situato nel semipiano superiore, entrante per il conduttore situato nel semipiano inferiore.
Il risultato è una coppia elettromagnetica (C) che tende a far ruotare la spira in modo da
allineare (nel verso concorde) il flusso di armatura con il flusso di eccitazione. Tale coppia sarà
diretta in modo da opporsi al moto del rotore4, ed avrà l’andamento qualitativo indicato in Fig.
4.9 analogo alla tensione indotta (valore massimo quando i due flussi sono perpendicolari tra
loro).
Pertanto, per effetto del commutatore a spazzole e lamelle, è possibile sviluppare una coppia
continua, nel senso del valor medio (Cm) non nullo. Estendendo il numero di spire si ottiene una
coppia sempre più costante. Ad esempio, nelle Fig. 4.10, Fig. 4.11 e Fig. 4.12 è illustrato il caso
(sempre elementare) di una macchina con due spire5.
C
Cm
0
π
2π
θr
Fig. 4.9 - Coppia prodotta con una sola spira di armatura
4
Concordemente alle convezioni adottate coppia e velocità sono discordi nel funzionamento da generatore.
Questo caso può essere compreso osservando che la seconda spira è sfasata di π/2 rispetto la prima, e le lamelle si estendono
anche per π/2.
5
54
Cap. 4 Macchina in corrente continua
4
π/4
1
2
3
Fig. 4.10 - Struttura elementare con due spire di armatura
π/2
ea
3-4
1-2
3-4
1-2
π/2
π
3π/2
Ea
0
2π
θr
π/4
Fig. 4.11 - Tensione indotta nel m.c.c con due spire di armatura
C
3-4
1-2
3-4
π/2
π
1-2
Cm
0
3π/2
2π
θr
Fig. 4.12 - Coppia prodotta nel m.c.c con due spire di armatura
d
φe
φa
π/2
ω
Fig. 4.13 - Flussi di eccitazione e di armatura con due spire di armatura (generatore)
Principio di funzionamento
4.2.2
55
Funzionamento da motore
ie
+
Pe
ia
ve
va
Pa
+
C,ω
Pm
Fig. 4.14 - Funzionamento da motore
Nel funzionamento da motore (Fig. 4.14) si alimentano gli avvolgimenti di eccitazione e di
armatura (ingressi) e si ricava in uscita potenza meccanica all’asse del motore sotto forma di
coppia e velocità di rotazione. In particolare, rispetto al caso del funzionamento da generatore,
il verso della corrente di armatura (ia) è opposto6.
Ciò vuol dire che il flusso di armatura è diretto anch’esso in modo opposto, rispetto al caso
del funzionamento da generatore7.
d
φe
φa
ω
Fig. 4.15 - Flussi di eccitazione e di armatura con due spire di armatura (motore)
Di conseguenza, anche la coppia elettromagnetica che tende a far ruotare la spira di rotore
per allineare i flussi di armatura ed eccitazione ha verso opposto rispetto al caso del
funzionamento da dinamo, e causa un movimento di rotazione nella sua stessa direzione
(l’andamento in funzione dell’angolo θr è lo stesso del caso di funzionamento da dinamo).
6
Concordemente alla convenzione dell’utilizzatore (C.d.U.) nell’avvolgimento di armatura la corrente fluisce dal morsetto a
potenziale maggiore verso quello a potenziale minor
7
In particolare il flusso di armatura è diretto sempre nel semipiano di sinistra della figura.
56
Cap. 4 Macchina in corrente continua
d
a
d
θr ∈(0,π)
C
C
φe
φe
A
1(+)
va
2(+)
+
+
1(-)
φa
B
B
ω
ia
va
2(-)
φa
a
A
ia
ω
θr ∈(π,2π)
Fig. 4.16 - Generazione del flusso di armatura nel funzionamento da motore
Estrapolando graficamente ad una macchina con un numero elevato di spire, il flusso di
armatura sarà fisso a π/2 gradi rispetto il flusso di eccitazione, le correnti nei conduttori di
rotore avranno verso concorde con tale flusso (considerando il funzionamento da motore o
dinamo) e le spazzole saranno disposte in quadratura (direzione q chiamata asse neutro) rispetto
al flusso di eccitazione, a significare il collegamento a conduttori che transitano in questa
posizione8.
La rappresentazione schematica della macchina in corrente continua nel funzionamento da
motore è illustrata in Fig. 4.17.
d
θr = π/2
ie
ve
q
a
ia
va
Fig. 4.17 - Rappresentazione di una m.c.c. funzionante da motore
8
Con tale disposizione, nella macchina reale le spazzole raccolgono la massima tensione indotta nell’avvolgimento di armatura.
Inoltre, durante la commutazione tra due lamelle successive, le spazzole vengono a corto-circuitare conduttori nei quali la
tensione indotta dal flusso di eccitazione è circa nulla, limitando la corrente di corto.
Determinazione del modello dal punto vista dei circuiti accoppiati
4.3
57
Determinazione del modello dal punto vista dei circuiti accoppiati
Abbiamo visto che il funzionamento del collettore a spazzole e lamelle fa sì che
l’avvolgimento di armatura, benché composto da conduttori rotanti e quindi soggetti a tensione
indotta dal flusso di eccitazione, generi a sua volta un flusso di armatura costantemente diretto
secondo l’asse q. Questo funzionamento deve essere tenuto in debita considerazione quando si
voglia determinare il modello analitico della macchina in corrente continua a partire dal metodo
generale dei circuiti magneticamente accoppiati.
A tale scopo, con riferimento alla rappresentazione in Fig. 4.17, immagineremo che
contrariamente a quanto accade nella macchina reale le spazzole ruotino solidalmente al rotore.
Di conseguenza, l’asse magnetico q dell’avvolgimento di armatura ruoterà con l’angolo θr.
Scriveremo quindi le equazioni per gli avvolgimenti di eccitazione ed armatura e
successivamente terremo conto del fatto che, nella macchina reale, la posizione dell’asse q è
fissata in θr = π/29.
4.3.1
Equazioni elettriche
Le equazioni elettriche degli avvolgimenti sono:
v a = Ra i a +
dψ a
dt
ψ a = La i a + M ae i a
avvolgimento di armatura
v e = Re i e +
dψ e
dt
ψ e = Le i e + M ae i e
avvolgimento di eccitazione
In esse, i coefficienti di auto e mutua induzione presenti nelle espressioni dei flussi avranno i
seguenti andamenti qualitativi in funzione di θr 10:
•
Induttanza propria dell’avvolgimento di eccitazione:
Le (θr ) = Le = costante
•
Induttanza propria dell’avvolgimento di armatura:
La(θr)
Lad
Laq
0
π/2
π
3π/2
2π
θr
Fig. 4.18 – Andamento qualitativo dell’induttanza propria dell’avvolgimento di armatura
9
Con questo procedimento è possibile utilizzare il metodo generale per la scrittura delle equazioni in una struttura
elettromagnetica avente circuiti sul rotore e sullo statore, tenendo conto poi qualitativamente del funzionamento del collettore.
Supporremo per semplicità di tipo sinusoidale gli andamenti periodici delle induttanze.
10
58
Cap. 4 Macchina in corrente continua
•
Induttanza mutua tra gli avvolgimenti di armatura ed eccitazione:
M ae (θr ) = −G ae sin θr
Mae(θr)
Gae
0
π/2
π
3π/2
θr
2π
-Gae
Fig. 4.19 – Andamento qualitativo dell’induttanza mutua armatura–eccitazione
Da tali andamento si deduce quanto segue:
- la derivata dell’induttanza propria dell’avvolgimento di eccitazione rispetto la posizione
θr è sempre identicamente nulla;
- la derivata dell’induttanza propria dell’avvolgimento di armatura rispetto la posizione
θr è nulla in corrispondenza di θr = π/2 dove l’induttanza ha un minimo;
- la derivata dell’induttanza mutua rispetto la posizione θr è del tipo (Fig. 4.20):
dM ae
= G ae cos θr
dθ r
dM ae
dθr
Gae
0
π/2
π
3π/2
2π
θr
-Gae
Fig. 4.20 – Andamento qualitativo della derivata dell’induttanza mutua armatura–eccitazione
e il suo valore calcolato in θr = π/2 vale:
dM ae
dθ r
π
2
= G ae
Sostituendo le espressioni dei flussi concatenati nelle equazioni delle tensioni degli
avvolgimenti si ottiene:
Determinazione del modello dal punto vista dei circuiti accoppiati
v a = Ra i a +
 di
d L dθ r
di
dM ae dθr
d
( La i a + M ae i e ) =  La a + i a a
+ M ae e + i e
dt
dt
dθ r dt
dt
d θ r dt

59


π

2
v e = Re i e +
 di
dL dθ r
di
dM ae dθr 
d

( Le i e + M ae i a ) =  Le e + i e e
+ M ae a + i a
dt
dt
dθ r d t
dt
dθr dt  π

2
e sostituendo le espressioni dei coefficienti induttivi e delle loro derivate calcolate in θr = π/2 si
ha:
v a = Ra i a + Laq
di a
dθ′
+ i e G ae r
dt
dt
v e = R e i e + Le
di e
dθ′′
+ i aG ae r
dt
dt
I termini del tipo “variazione della posizione nel tempo” sono stati distinti nelle equazioni di
armatura ed eccitazione in quanto:
-
dθ′r dt nell’equazione di armatura, rappresenta la velocità relativa tra il flusso di eccitazione e
le bobine di armatura; effettivamente, essa coincide con la velocità di rotazione del rotore ωr;
-
dθ′r′ dt nell’equazione di eccitazione, rappresenta la velocità relativa tra il flusso di armatura e
le bobine di campo; tale velocità è nulla, in quanto le bobine di campo sono ferme rispetto al
flusso di armatura.
Pertanto, dalle precedenti considerazioni, ponendo per comodità La = Laq, si ottengono le
seguenti equazioni elettriche della macchina in corrente continua:
v a = Ra i a + La
di a
+ G ae i e ω r
dt
tensione di armatura
(4.4)
v e = R e i e + Le
di e
dt
tensione di eccitazione
(4.5)
Considerando anche le equazioni dei flussi, si è soliti definire:
φ a = La i a
flusso di armatura11
(4.6)
φ e = Le i e
flusso di eccitazione
(4.7)
tensione di armatura
(4.8)
da cui si trova anche:
v a = Ra i a +
11
dφ a
+ G ae i e ω r
dt
Tale flusso coincide con il flusso proprio di armatura.
60
Cap. 4 Macchina in corrente continua
v e = Re i e +
dφ e
dt
tensione di eccitazione
(4.9)
Nell’equazione della tensione di armatura, il termine proporzionale alla velocità di rotazione
rappresenta la tensione indotta, che considerando il legame (4.7) tra flusso e corrente di
eccitazione si può scrivere:
e = G ae i e ω r = k e φ e ω r
tensione indotta
(4.10)
avendo definito il coefficiente12:
k e = G ae ⋅ (i e φ e ) = G ae Le
4.3.2
(4.11)
Espressione della coppia
Per quanto riguarda la coppia elettromagnetica, nel caso di una struttura elettromagnetica
con un avvolgimento sullo statore (1) ed uno sul rotore (2) si aveva l’espressione generale:
C=
dM ( θ r ) 1 2 dL 2 ( θ r )
1 2 d L1 ( θ r )
+ i1i 2
+ i2
i1
2
2
dθ r
dθ r
dθ r
Procedendo come al paragrafo precedente, si può specializzare tale espressione per la
macchina in corrente continua considerando il valore delle derivate dei coefficienti induttivi in
θr = π/2. Sostituendo e → 1 ed a → 2 si ha:
 1 d L (θ )
dM ae (θr ) 1 2 dLe (θr ) 

C =  i a2 a r + i a i e
+ ie
dθr
dθ r
dθr  π
2
2
2
dalla quale si ricava immediatamente:
C = G ae i a i e
(4.12)
In base alle (4.7) e (4.11), la coppia elettromagnetica si può anche scrivere in funzione del
flusso di eccitazione e della corrente di armatura:
C = ke φ e ia
4.3.3
(4.13)
Rappresentazione circuitale
Le equazioni elettriche e l’espressione della coppia, insieme all’equazione di equilibrio
meccanico, definiscono il modello elettromagnetico della macchina in corrente continua. La
rappresentazione circuitale associata è illustrata in Fig. 4.21.
12
Il coefficiente ke risulta costante in ipotesi di linearità del circuito magnetico.
Test di apprendimento
61
Ra
+
La
+
ia(t)
e(t)
va(t)
c(t)
_
Le
Re
ie(t)
_
+
ve(t)
_
ωr(t)
cr(t)
Fig. 4.21 – Rappresentazione circuitale della macchina in corrente continua
Test di apprendimento
1) Descrivere la struttura di base di una macchina in corrente continua.
2) Descrivere il collettore a lamelle e spazzole.
3) Disegnare lo schema elementare di una macchina in c.c. individuando le “porte” di
potenza elettrica e meccanica.
4) Descrivere il funzionamento della macchina in c.c. da dinamo e da motore. Disegnare i
flussi di potenza negli avvolgimenti di eccitazione ed armatura per i due tipi di
funzionamento.
5) Cosa si intende per tensione nell’avvolgimento di armatura? Ricavarne l’andamento nel
funzionamento da dinamo a vuoto per la macchina con una sola spira di armatura.
6) Descrivere la generazione del flusso di armatura nel funzionamento da motore della
macchina con una sola spira di armatura.
7) Descrivere il principio di generazione della coppia nel funzionamento da motore.
Ricavarne l’andamento qualitativo per la macchina con una sola spira di armatura.
8) Disegnare la struttura di una macchina con più spire di armatura nel funzionamento da
motore e generatore, precisando il verso della corrente nei conduttori.
9) Ricavare il modello elettrico del motore in c.c. a partire dall’analisi dei circuiti
magneticamente accoppiati.
10) Ricavare l’espressione della coppia elettromagnetica a partire dall’espressione generale
per circuiti magneticamente accoppiati.
11) Esprimere il modello elettrico e la coppia in termini di flusso oppure di corrente di
eccitazione.
12) Esprimere la tensione indotta in termini di flusso oppure di corrente di eccitazione.
13) Disegnare lo schema circuitale di una macchina in corrente continua.
62
Cap. 4 Macchina in corrente continua
Indice delle figure
Fig. 4.1 - Struttura elementare del motore in corrente continua.................................................................................. 49
Fig. 4.2 - Percorso del flusso di eccitazione .................................................................................................................. 49
Fig. 4.3 - Schema elementare della macchina in corrente continua............................................................................. 50
Fig. 4.4 - Funzionamento da generatore a vuoto ......................................................................................................... 51
Fig. 4.5 - Tensione indotta nella spira elementare ....................................................................................................... 51
Fig. 4.6 - Funzionamento da generatore a carico......................................................................................................... 52
Fig. 4.7 - Generazione del flusso di armatura nel funzionamento da generatore......................................................... 52
Fig. 4.8 - Flussi di eccitazione e di armatura con una sola spira di armatura............................................................... 53
Fig. 4.9 - Coppia prodotta con una sola spira di armatura .......................................................................................... 53
Fig. 4.10 - Struttura elementare con due spire di armatura ......................................................................................... 54
Fig. 4.11 - Tensione indotta nel m.c.c con due spire di armatura................................................................................ 54
Fig. 4.12 - Coppia prodotta nel m.c.c con due spire di armatura ................................................................................ 54
Fig. 4.13 - Flussi di eccitazione e di armatura con due spire di armatura (generatore) ................................................ 54
Fig. 4.14 - Funzionamento da motore.......................................................................................................................... 55
Fig. 4.15 - Flussi di eccitazione e di armatura con due spire di armatura (motore)...................................................... 55
Fig. 4.16 - Generazione del flusso di armatura nel funzionamento da motore ............................................................ 56
Fig. 4.17 - Rappresentazione di una m.c.c. funzionante da motore............................................................................. 56
Fig. 4.18 – Andamento qualitativo dell’induttanza propria dell’avvolgimento di armatura ........................................ 57
Fig. 4.19 – Andamento qualitativo dell’induttanza mutua armatura–eccitazione ....................................................... 58
Fig. 4.20 – Andamento qualitativo della derivata dell’induttanza mutua armatura–eccitazione ................................. 58
Fig. 4.21 – Rappresentazione circuitale della macchina in corrente continua ............................................................. 61
INDICE
4
Macchina in corrente continua ..............................................................................49
4.1
Struttura e schema elementare .................................................................................49
4.2
Principio di funzionamento .........................................................................................50
4.2.1
Funzionamento da generatore ............................................................................................ 50
4.2.1.1
4.2.1.2
4.2.2
4.3
4.3.1
4.3.2
4.3.3
Funzionamento da generatore a vuoto................................................................................................. 50
Funzionamento da generatore a carico ................................................................................................ 52
Funzionamento da motore ................................................................................................. 55
Determinazione del modello dal punto vista dei circuiti accoppiati .......................57
Equazioni elettriche ............................................................................................................ 57
Espressione della coppia ..................................................................................................... 60
Rappresentazione circuitale................................................................................................ 60
Test di apprendimento ..............................................................................................................61
Indice delle figure .......................................................................................................................62
INDICE ........................................................................................................................................62