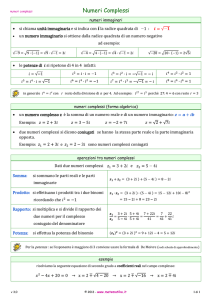
1
I Numeri Complessi
L’esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni
sui numeri reali R non sempre sono possibili.
• x2 + 1 = 0 ?
• log(−10) ?
• log−2 3 ?
•
√
−1?
Allo scopo di ovviare a questa carenza si introducono i numeri complessi. I numeri
complessi C sono coppie ordinate di numeri reali
C = {(a, b), a, b ∈ R}
In particolare i numeri del tipo (a, 0) vengono considerati identici al numero reale a.
Il numero complesso (0, 1) si denota con i e si chiama unità immaginaria dei numeri
complessi, Il numero i è tale che i2 = −1. Con l’introduzione dell’unità immaginaria
i numeri complessi si possono allora rappresentare anche nella forma a + ib, dove
a rappresenta la parte reale del numero complesso: a = <(z) e b la sua parte
immaginaria, b = =(z). Due numeri complessi a + ib , c + id coincidono se e solo se
a = c, b = d.
Potenze di i:
i0 = 1
i1 = i
i2 = −1
i3 = −i
i4 = 1
i5 = i
i6 = −1
i7 = −i
...
4n
i
1.1
4n+1
=1 i
= i i4n+2 = −1 i4n+3 = −i
Operazioni fondamentali con i numeri complessi
addizione: (a + ib) + (c + id) = (a + c) + i(b + d),
sottrazione: (a + ib) − (c + id) = (a − c) + i(b − d),
moltiplicazione: (a + ib) · (c + id) = (ac − bd) + i(ad + bc),
1
reciproco: se w = c + id 6= 0 allora
1
c
d
= 2
−i 2
,
2
w
c +d
c + d2
a + ib
ac + bd
bc − ad
= 2
+i 2
con c2 + d2 > 0,
2
c + id
c +d
c + d2
√
valore assoluto: |a + ib| = a2 + b2 ,
divisione:
complesso coniugato: se z = a + ib allora z = a − ib,
opposto: se z = a + ib allora −z = −a − ib.
Se z = a + ib allora risulta z + z = 2a ∈ R, z − z = 0, z + (−z) = 2ib ∈ C \ R.
É possibile eseguire le operazioni sui numeri complessi con le regole del calcolo dei
numeri reali trattando i come un numero reale, con l’accortezza di sostituire i2 con
-1. Ad esempio z · w = (a + ib) · (c + id) = ac + iad + ibc + i2 bd = (ac − bd) + i(bc + ad).
1.2
Rappresentazione geometrica dei numeri complessi
L’addizione dei numeri complessi corrisponde alla regola del parallelogramma per la
somma di vettori:
2
1.3
La forma trigonometrica dei numeri complessi
Introducendo nel piano complesso le coordinate polari al posto delle coordinate cartesiane si ottiene una nuova rappresentazione dei numeri complessi:
x = r cos t, y = r sin t
il numero complesso z = x + iy = r(cos t + i sin t) dove
p
r = x2 + y 2 ( r è il modulo di z) e t (detto argomento o anomalia) è l’angolo
formato tra la direzione positiva dell’asse delle x e la semiretta che congiunge l’origine
con il punto z. L’argomento è definito a meno di multipli dell’angolo giro.
Dato un numero complesso a + ib, il suo modulo è dato da r =
p
x2 + y 2 e, se
esso è diverso da zero, il suo argomento t è determinato da
sin t = p
a
cos t = p
2
x + y2
b
x2
+
y2
Utilizzando questa rappresentazione il prodotto di due numeri complessi diventa particolarmente semplice:
z = r(cos t + i sin t), w = s(cos u + i sin u), zw = rs(cos(t + u) + i sin(t + u))
dunque, per moltiplicare due numeri complessi si moltiplicano i moduli e si sommano
gli argomenti. La formula
(cos t + i sin t)(cos u + i sin u) = cos(t + u) + i sin(t + u)
3
è detta formula di De Moivre e permette di calcolare la potenza n-esima di un numero
complesso z:
z n = [r(cos t + i sin t)]n = rn (cos nt + i sin nt), n ∈ N.
Chiamiamo radice n-esima di z ogni numero complesso w tale che wn = z. Tale
equazione ammette esattamente n soluzioni; se z = r(cos t + i sin t) allora
w = r1/n (cos(t + 2kp)/n + i sin(t + 2kp)/n), k = 0, 1, ..., n − 1.
I valori di w1 , . . . , wn sono regolarmente distribuiti lungo la circonferenza avente centro nell’origine raggio pari a r1/n . Le radici sono dunque rappresentate dai vertici di
un poligono regolare.
Determiniamo ad esempio le radici del numero complesso z = (−1+i)1/3 . Risulta
−1 + i = 21/2 [cos(3π/4 + 2kp) + i sin(3π/4 + 2kp)]
(−1 + i)1/3 = 21/6 [cos(3π/4 + 2kp)/3 + i sin(3π/4 + 2kp)/3].
Dunque
• per k = 0, z1 = 21/6 [cos π/4 + i sin π/4]
• per k = 1, z2 = 21/6 [cos 11π/12 + i sin 11π/12]
• per k = 2, z3 = 21/6 [cos 19π/12 + i sin 19π/12].
4
1.4
Definizione di ex nel campo complesso1
Vogliamo ora estendere la definizione di ex in modo che abbia significato anche nel
campo complesso e che conservi la legge degli esponenti: ea · eb = ea+b . Se poniamo
z = x + iy, per la legge degli esponenti deve risultare: ez = ex+iy = ex · eiy . Dobbiamo
quindi capire che valore assegnare al numero complesso eiy . Supponiamo che, al
variare di y, eiy = a(y) + ib(y), con a, b funzioni derivabili almeno due volte. Se
deriviamo due volte otteniamo:
eiy = a(y) + ib(y)
ieiy = a0 (y) + ib0 (y)
−eiy = a00 (y) + ib00 (y)
Inoltre, poiché e0 = 1, risulta a(0) = 1, a0 (0) = 0, b(0) = 0, b0 (0) = 1. Dalla prima e
dalla terza equazione, si ottiene
a00 (y) = −a(y),
b00 (y) = −b(y)
e da queste due equazioni, unitamente ai valori di a e b prima trovati si ottiene
a(y) = cos(y), b(y) = sin(y)
e dunque
eiz = ex (cos(y) + i sin(y)).
Da tale formula possiamo ottenere:
eit = cos t + i sin t
e−it = cos t − i sin t
e dunque sommando o sottraendo membro a membro otteniamo:
sin t =
eit − e−it
eit + e−it
, cos t =
,
2i
2
e, per t 7→ nt,
sin nt =
1
eint − e−int
eint + e−int
, cos nt =
.
2i
2
la soluzione delle equazioni che compaiono in questa nota verranno studiate nel corso di Analisi
Matematica II.
5
Infine, se z = a + ib,
|ez | = ea |eb | = ea
1.5
p
cos2 b + sin2 b = ea .
La funzione logaritmo
Se z 6= 0 il ln z indica un qualunque numero w ∈ C per cui risulta
ew = z.
(1)
Scrivendo z nella forma esponenziale: z = reit = eln r+it ne segue che una soluzione
di (1) è ln r + it. Ricordando poi che la funzione esponenziale nel campo complesso
è periodica di periodo 2πi, si ha che tutte le soluzioni di (1) sono date da:
w = ln r + i(t + 2kπ), k ∈ Z.
Il logaritmo di un numero complesso z 6= 0 nella base complessa w 6= 0 è dato da:
logw z =
6
ln z
.
ln w