Circuiti a scatto:11 esercizi risolti

Edutecnica.it – Circuiti a scatto -Esercizi
1
Soluzione a pag.5
Esercizio no.1
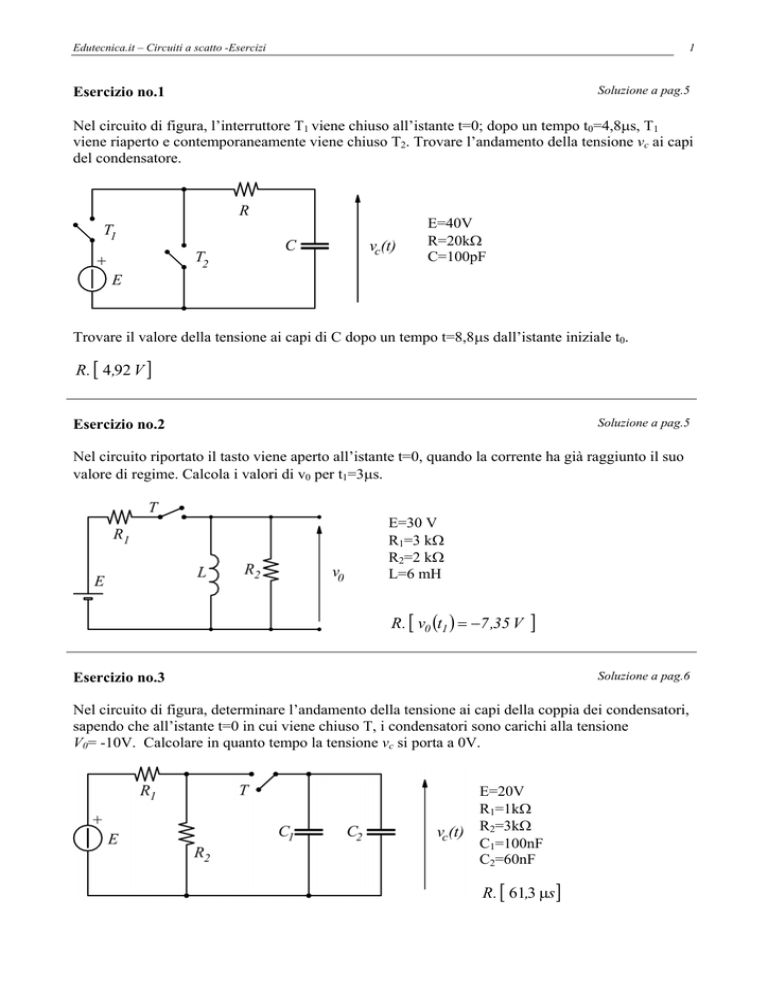
Nel circuito di figura, l’interruttore T1 viene chiuso all’istante t=0; dopo un tempo t0=4,8µs, T1
viene riaperto e contemporaneamente viene chiuso T2. Trovare l’andamento della tensione vc ai capi
del condensatore.
E=40V
R=20kΩ
C=100pF
Trovare il valore della tensione ai capi di C dopo un tempo t=8,8µs dall’istante iniziale t0.
R . [ 4 ,92 V ]
Soluzione a pag.5
Esercizio no.2
Nel circuito riportato il tasto viene aperto all’istante t=0, quando la corrente ha già raggiunto il suo
valore di regime. Calcola i valori di v0 per t1=3µs.
E=30 V
R1=3 kΩ
R2=2 kΩ
L=6 mH
R. [ v0 (t1 ) = −7 ,35 V
]
Soluzione a pag.6
Esercizio no.3
Nel circuito di figura, determinare l’andamento della tensione ai capi della coppia dei condensatori,
sapendo che all’istante t=0 in cui viene chiuso T, i condensatori sono carichi alla tensione
V0= -10V. Calcolare in quanto tempo la tensione vc si porta a 0V.
E=20V
R1=1kΩ
R2=3kΩ
C1=100nF
C2=60nF
R. [ 61,3 µs ]
Edutecnica.it – Circuiti a scatto -Esercizi
2
Soluzione a pag.7
Esercizio no.4
Nel circuito di figura, inizialmente i tasti T1 e T2 sono aperti e il condensatore C è scarico.
All’istante t=0, viene chiuso il tasto T1, dopo un tempo t=42ms si chiude pure T2. Si trovi il valore
di vc dopo un tempo t=82ms dalla chiusura del primo deviatore
E=4V
R1=20kΩ
R2=2kΩ
C=10µF
R . [ vc = 3,94 V
]
Soluzione a pag.07
Esercizio no.5
Il condensatore C è carico alla tensione VC0=50V con la polarità indicata mentre gli interruttori
sono aperti.All’istante t=0 viene chiuso T1, quindi dopo 20ms viene chiuso T2. Calcola il valore
della tensione VAB dopo 30 ms dal tempo t=0.
E=80 V
R1=10 kΩ
R2=20 kΩ
R3=30 kΩ
VCO=50 V
C=1 µF
R . [ 54,98 V ]
Soluzione a pag.9
Esercizio no.6
Nel circuito illustrato, i deviatori sono inizialmente aperti ed il condensatore è scarico.
I deviatori vengono chiusi nel seguente ordine: T1 per t1=0, T2 per t2=280µs e T3 per t3=520µs.
Descrivere l’andamento della VAB nel tempo e calcolare il valore della VAB dopo un tempo
tx=550µs.
E=80 V
R1=100 kΩ
R2=400 kΩ
R3=10 kΩ
C=1000 pF
R . [ v AB (t x ) = −9 V ]
Edutecnica.it – Circuiti a scatto -Esercizi
3
Soluzione a pag.10
Esercizio no.7
Nel circuito illustrato, disegnare l’andamento della tensione di uscita VAB a partire dall’istante t=0
di chiusura del tasto T. Calcola, inoltre il valore della corrente circolante dopo un tempo tx=0,5µs
dalla chiusura del tasto.
E=100 V
R1=2 kΩ
R2=3 kΩ
L=1 mH
R . [ iL (t x ) = 18,35 V ]
Soluzione a pag.11
Esercizio no.8
Nel circuito, il tasto T viene chiuso quando la corrente è già a regime, trovare l’andamento della
tensione ai capi dell’induttanza e il valore della corrente dopo 0,5ms dalla chiusura del tasto.
E=42 V
R1=1 kΩ
R2=0,4 kΩ
L=0,28 H
R. [ iL (0,5ms ) = 40 mA ]
Soluzione a pag.12
Esercizio no.9
Il circuito riportato è a regime, quando viene chiuso il tasto T1; dopo un tempo t0=5µs viene chiuso
il tasto T2. Descrivi l’andamento della tensione VAB .
E=100 V
R1=20 kΩ
R2=8 kΩ
R=12 kΩ
L=10 mH
Edutecnica.it – Circuiti a scatto -Esercizi
4
Soluzione a pag.13
Esercizio no.10
Il circuito è sottoposto in ingresso ad un treno di onde rettangolari con ampiezza E=24V, TL=20 µs
TH=10 µs (T=TL+TH=30µs). Trovare l’andamento del segnale di uscita sapendo che C=125pF ed
R=16kΩ.
Soluzione a pag.14
Esercizio no.11
Il segnale di ingresso della rete illustrata è una forma d’onda rettangolare simmetrica di ampiezza
Ei=10V con periodo T=2TL=2TH=16 µs. La tensione ai capi dell’induttanza deve avere a regime
come valori estremi dell’esponenziale decrescente positivo V1=6V e V2=3V. Calcolare i valori R1
ed L nel caso la resistenza di carico sia RL=80kΩ.
[
R. R1 = 53,3 kΩ L = 0 ,184 mH
]
Edutecnica.it – Circuiti a scatto -Esercizi
5
Esercizio no.1:soluzione
Dopo la chiusura dell’interruttore T1, la tensione vc
cresce esponenzialmente con legge:
(
vc (t ) = E ⋅ 1 − e −t / RC
)
t


vc (t ) = 40 ⋅ 1 − exp  −
 2 ⋅ 10 −6


 il valore raggiunto dopo 4,8µs è:


 4 ,8 ⋅ 10 −6
vc1 = 40 ⋅ 1 − exp  −
−6
 2 ⋅ 10


 = 36 ,4 V


dall’istante t0=4,8µs in poi, il condensatore si scarica attraverso la resistenza partendo dal valore
raggiunto vc1=36,4V secondo la legge:
vc (t ) = VC 0 e
− (t − t 0 ) / RC
 (8 ,8 − 4 ,8 ) ⋅ 10 −6 
 t − t0 
= 36 ,4 ⋅ exp  −
 = 36 ,4 ⋅ exp −
 = 4 ,92 V
−6
⋅
2
10
 RC 


Esercizio no.2:soluzione
A regime, prima della apertura di T l’induttanza L si comporta come un corto circuito percorsa dalla
corrente i = E / R1 = 30 / 3 = 10 mA con v0=0. All’apertura di T il transitorio sull’induttore è
regolato dalla:
(
)
iL (t ) = i f − i f − ii ⋅ e −tR / L
con i f = 0 e ovviamente ii =
L 6 ⋅ 10 −3
E
la costante di tempo τ =
=
= 3 µs
R2
R1
2 ⋅ 10 3

E
E −t / τ
iL (t ) = 0 −  0 −  ⋅ e −t / τ =
⋅e
R
R

1
1
→
v0 (t ) = − R2 ⋅ iL (t ) = −
v0 (t1 ) == −
ER2 −t / τ
⋅e
R1
20
2 ⋅ 30 − 3 / 3
⋅e
=−
= −7 ,35 V
e
3
Edutecnica.it – Circuiti a scatto -Esercizi
6
Esercizio no.3:soluzione
I due condensatori in parallelo equivalgono all’unico condensatore:
C = C1 + C2 = 160 nF
A monte del deviatore T il circuito può essere semplificato col teorema di Thevenin.
Il generatore equivalente vale: Eq =
ER2
20 ⋅ 3
=
= 15 V
R1 + R2
4
La resistenza equivalente vale Rq = R1 // R2 =
3
= 0 ,75 kΩ
4
Dobbiamo pensare che a regime il condensatore
C si carichi alla tensione del generatore E.
Quindi vf = E mentre vi = V0.
Il fenomeno del transitorio di accensione è
regolato, in questo caso, dall’equazione:
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC = E − (E − V0 ) ⋅ e −t / RC
è possibile individuare l’istante tz di
attraversamento dell’asse a 0 V tramite
l’equazione:
0 = E − (E − V0 ) ⋅ e −t / RC
(E − V0 ) ⋅ e−t / RC = E
per cui: −
 E 
tz
= ln 
 →
RqC
 (E − V0 )
che diventa:
→ e −t / RC =
 E 
t z = − RqC ln 

 (E − V0 )
 15 
 15 
t z = −0 ,75 ⋅ 10 3 ⋅ 160 ⋅ 10 − 9 ln 
= −120 ⋅ 10 −6 ln   = 61,3 µs

 25 
 (15 + 10 ) 
E
(E − V0 )
Edutecnica.it – Circuiti a scatto -Esercizi
7
Esercizio no.4:soluzione
Nel primo intervallo di tempo, da 0 a 42ms il circuito
ha la configurazione riportata. Poniamo:
R = R1 + R2 = 22 kΩ
C inizia a caricarsi con andamento esponenziale
crescente, all’istante t0=42ms si ha:
(
vc (t0 ) = V0 = E ⋅ 1 − e
− t 0 / RC
)


42 ⋅ 10 − 3 
42 


 = 4 ⋅ 1 − exp  −
= 4 ⋅ 1 − exp  −
 = 0 ,695 V
3
− 5 
 220 


 22 ⋅ 10 ⋅ 10 
Dopo la chiusura del secondo deviatore il circuito
diventa come illustrato in figura; applichiamo la:
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC
sostituendo i valori:

82 ⋅ 10 −3 
vc (t1 ) = E − (E − V0 ) ⋅ e −t / R C = 4 − (4 − 0 ,695) exp −
=
3
−5 
2
⋅
10
⋅
10


 82 
= 4 − 3,3 exp  −  = 3,94 V
 20 
2
Esercizio no.5:soluzione
Dall’istante t=0 all’istante t0=20ms C si scarica attraverso la serie
delle due resistenze R2 ed R3.
La corrente circolante ha espressione:
i=
VCO
e−t / (R
R2 + R3
2
+ R3 )C
=
50
e − t / 0 ,05 mA
3
50 ⋅ 10
per cui VAB = i ⋅ R3 = 30 ⋅ e −t / 0 ,05 dopo un tempo t0=20ms=0,02s
VAB (t0 ) = i ⋅ R3 = 30 ⋅ e −0 ,02 / 0 ,05 = 20 V
Edutecnica.it – Circuiti a scatto -Esercizi
da notare come al tempo t=0 sia: VAB (0 ) = i ⋅ R3 = 30 ⋅ e −0 / 0 ,05 = 30 V
per la tensione sul condensatore si ha:
VAB = VCO ⋅ e −t / ( R
2
+ R3 )C
= 50 ⋅ e −t / 0 ,05 al tempo t0=20ms
Vc = 50 ⋅ 0 ,67 = 33,5 V
Dall’istante t0=20ms in poi il condensatore riprende a caricarsi con costante di tempo:

RR 
T =  R2 + 1 3  C = 27 ,5 ms
R1 + R3 

Infatti applicando il teorema di Thevenin fra i morsetti AB
Eq =
ER3
80 ⋅ 30
=
= 60 V
R1 + R3 10 + 30
Rq =
R1 R3
= 7 ,5 kΩ
R1 + R3
La corrente di carica del condensatore ha quindi l’espressione:
i=
Eq − Vc
Rq + R2
e − (t −t ) / T =
0
60 − 33,5
26 ,5
 t − 0 ,02 
 t − 0 ,02 
exp  −
exp  −
=

3
3
(20 + 7 ,5 ) ⋅ 10
 0 ,0275  27 ,5 ⋅ 10
 0 ,0275 
 t − 0 ,02 
VAB = Eq − Rqi = 60 − 7 ,22 exp  −
 dopo 30 ms dal tempo t=0.
 0 ,0275 
 0,03 − 0 ,02 
VAB = Eq − Rqi = 60 − 7 ,22 exp  −
 = 54 ,98 V
0 ,0275 

da notare come subito dopo l’istante t0=20ms la VAB riprenda dal valore:
8
Edutecnica.it – Circuiti a scatto -Esercizi
9
VAB = 60 − 7 ,22 e −0 / 0 ,0275 = 60 − 7 ,22 = 52,78 V
Esercizio no.6:soluzione
Alla chiusura del deviatore T1 la tensione vAB comincia a crescere esponenzialmente (è negativa,
data la disposizione della batteria)
(
v AB = − E ⋅ 1 − e −t / R C
1
)
con
R1C=100 µs
per t2=280µs la VAB assume il valore:
(
v AB (t2 ) = − E ⋅ 1 − e
− t 2 / R1C
)

 280 ⋅ 10 −6
= −80 ⋅ 1 − exp  −
−6

 100 ⋅ 10

 = −80 ⋅ 0 ,039 = −75V = VAB


all’istante t2=280 µs si chiude il deviatore T2 e ovviamente, riduciamo il circuito col teorema di
Thevenin.
Eq =
ER2
= 64 V
R1 + R2
Rq = R1 // R2 = 80 kΩ
con Rq C = 80 µs
Il condensatore si scarica parzialmente, tendendo a raggiungere il valore di Eq secondo la regola:
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC
→
(
)
v AB = Eq − Eq − VAB ⋅ e
− t / Rq C
 (t − t2 ) 
 240 
v AB = −64 − [− 64 − (− 75 )] exp −
=
 = −64 − 11 exp −
 80 
 RqC 
v AB = −64 − 11 ⋅ 0 ,05 = −64 ,5 V = VAB 2
Edutecnica.it – Circuiti a scatto -Esercizi
10
All’istante t3=520 µs si chiude T3 e l’intero circuito si semplifica col teorema di Thevenin,
ottenendo:
Ex =
Eq R3
= 7 ,1 V
Rq + R3
Rx = Rq // R3 = 8 ,9 kΩ
con
RxC = 8,9 µs
Il condensatore si scarica ulteriormente secondo la regola:
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC
→
v AB = E x − (Ex − VAB 2 ) ⋅ e −t / R C
x
 (t − t3 )
 (t − t3 )
= −7 ,1 − 57 ,4 exp −
v AB = −7 ,1 − [− 7 ,1 − (− 64 ,5 )] exp −


 RxC 
 RxC 
al tempo tx=550µs avremo:
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC
→
v AB = Ex − (Ex − VAB 2 ) ⋅ e −t / R C
x
 (550 − 520 )
v AB = −7 ,1 − 57 ,4 exp −
 = −9 V
8 ,9

Esercizio no.7:soluzione
Alla chiusura del deviatore T la costante di tempo che governa il circuito è:
τ=
L
= 0 ,2 µs
R1 + R2
A regime l’induttanza si comporta come un corto circuito mentre alla chiusura del tasto come un
circuito aperto, per cui nella:
Edutecnica.it – Circuiti a scatto -Esercizi
(
11
)
iL (t ) = i f − i f − ii ⋅ e −tR / L
if =
avremo
(
E
= 20 mA e
R1 + R2
ii = 0
)

 0 ,5 
iL (t x ) = 20 − (20 − 0 ) ⋅ e −t / τ = 20 ⋅ 1 − e −t / τ = 20 ⋅ 1 − exp  −
 = 18 ,35 V
 0 ,2 

L’espressione della VAB è ricavabile dalla legge di Kirchoff:
se per t=0 il circuito è aperto si ha VAB=E mentre iL (t → ∞ ) = 20 mA
v AB = E − R1iL
quindi v AB (t → ∞ ) = E − R1iL = 100 − 2 ⋅ 20 = 60 V
tutte le variazioni hanno un andamento esponenziale
Esercizio no.8:soluzione
E
42
=
= 30 mA
R1 + R2 1,4
E
Alla chiusura di T la nuova corrente a regime sarà i f =
= 42 mA quindi la
R1
Prima della chiusura del tasto: ii =
(
)
iL (t ) = i f − i f − ii ⋅ e −tR / L
co τ =
L 0 ,28
=
= 280 µs
R1 1000
→
iL (t ) = 42 − (42 − 30 ) ⋅ e −t / τ
 500 
iL (0 ,5ms ) = 42 − (42 − 30 ) ⋅ exp  −
 = 40 mA
 280 
La iL ha, dunque un andamento esponenzialmente crescente fra 30 e 42 mA a cui tende
asintoticamente.
vL (0 ) = 12 V
vL = E − R1i = 12e − t / τ = 
vL (t → ∞ ) = 0 V
Edutecnica.it – Circuiti a scatto -Esercizi
12
Esercizio no.9:soluzione
Prima della chiusura del deviatore T1 la corrente i vale: i = I 0 =
E
100
=
= 5 mA
R + R2
20
La tensione VAB, sempre prima della chiusura del tasto T1: v AB = VAB0 = RI 0 = 60 V
Alla chiusura del tasto T1, la corrente nell’induttanza L resta inizialmente al valore I0, mentre nella
resistenza R1 circolerà una corrente I, per cui in tale istante la corrente erogata dal generatore:
i (0 ) = I + I0 e quindi si avrà:
E = R1 I + R2 (I + I 0 )
E − R2 I 0 100 − 8 ⋅ 10 3 ⋅ 5 ⋅ 10 −3
I=
=
= 2 ,14 mA
R1 + R2
28 ⋅ 10 3
→
Quindi la corrente erogata dal generatore E sarà:
i = I + I 0 = 5 + 2 ,14 = 7 ,17 mA
e tenderà al nuovo valore di regime:
I1 =
E
100
=
= 6 ,45 mA
R2 + (R // R1 ) 8 + 7,5
(l’induttanza L si comporta a regime come un corto circuito). Durante il transitorio la i erogata dal
generatore varierà con legge:
(
)
i = i f − i f − ii ⋅ e −tR / L
con τ =
L
Rx
dove
→
Rx = R +
10 ⋅ 10 −3
τ=
= 0 ,565 µs
17 ,72 ⋅ 10 3
i = I 1 − [I 1 − (I + I 0 )] e −t / τ
8 ⋅ 20
R1 R2
= 12 +
= 17 ,72 kΩ
R1 + R2
28
per cui
la legge di variazione della i:
t


i = 6 ,45 + 0 ,69 exp  −
 mA
−6
 0 ,565 ⋅ 10 
di conseguenza:
t
t




v AB = E − R2i = 100 − 51,6 − 5 ,52 exp  −
 = 48 ,4 − 5 ,52 exp  −

−6
−6
 0 ,565 ⋅ 10 
 0 ,565 ⋅ 10 
tende al valore v AB = 48 ,4 V
Edutecnica.it – Circuiti a scatto -Esercizi
13
all’istante t0=5 µs in cui viene chiuso il tasto T2, il transitorio precedente è praticamente terminato e
la corrente i si porta istantaneamente al valore
i=
E 100
=
= 12 ,5 mA
R2
8
mentre la vAB si porta istantaneamente a 0 V.
Esercizio no.10:soluzione
La forma d’onda di uscita sarà una successione di esponenziali crescenti e decrescenti regolati dalle
equazioni di carica e scarica del condensatore.
per la carica
(
)
vc (t ) = v f − v f − vi ⋅ e −t / RC
per la scarica vc (t ) = vi ⋅ e −t / RC
più precisamente avremo, durante la carica:
vc (t ) = E − (E − VB ) ⋅ e −t / RC osservando il primo gradino di tensione:
VA = E − (E − VB ) ⋅ e −TH / τ con
τ = RC = 125 ⋅ 10 −12 ⋅ 16 ⋅ 10 3 = 2 µs
durante la scarica:
vc (t ) = VA ⋅ e −t / τ
→
VB = VA ⋅ e −TL / τ
sostituendo la seconda equazione nella prima..
(
)
V A = E − E − V A ⋅ e −T L / τ ⋅ e −T H / τ
ma e
−T L / τ
→
⋅ e −TH / τ = e −(TH +TL ) / τ = e −T / τ
(
)
VA = E ⋅ 1 − e −TH / τ + VA ⋅ e −TL / τ ⋅ e −TH / τ
per cui:
Edutecnica.it – Circuiti a scatto -Esercizi
(
VA ⋅ 1 − e
−T / τ
) = E ⋅ (1 − e
14
−TH / τ
)
1 − e −TH / τ
VA = E ⋅
1 − e −T / τ
→
1 − e −10 / 2
1 − e −5
VA = 24 ⋅
= 24 ⋅
= 23 ,83 V ≅ 24 V
1 − e − 30 / 2
1 − e −15
VB = VA ⋅ e −TL / τ = 23,83 ⋅ e −20 / 2 = 23,83 ⋅ e −10 ≅ 0 V
Esercizio no.11:soluzione
E’ chiaro che il circuito deve preventivamente essere semplificato col teorema di Thevenin:
E=
Ei RL
R1 + RL
R = R1 // RL
Così semplificato il circuito è riconducibile ad una cella R-L con la corrente che percorre
l’induttanza regolata dalla:
(
)
iL (t ) = i f − i f − ii ⋅ e −tR / L
v0 = E − Ri
e con
applicando la precedente al primo gradino di tensione:
iL (t ) =
(
E E
E

−  − 0  ⋅ e−tR / L = ⋅ 1 − e −t / τ
R R
R

v0 ( t ) = E − R ⋅
(
)
(
)
quindi avremo:
)
E
⋅ 1 − e −t / τ = E − E ⋅ 1 − e −t / τ = E ⋅ e −t / τ
R
con riferimento alla figura riportata sopra, avremo V1 = v0 (t = 0 ) = E = 6 V quindi
E=
Ei RL
R1 + RL
→
6=
10 ⋅ 80
R1 + 80
→ R1 + 80 =
800
6
→
R1 =
800
− 80 = 53,3 kΩ
6
Edutecnica.it – Circuiti a scatto -Esercizi
essendo R = R1 // RL =
15
53,3 ⋅ 80
= 32 kΩ
80 + 53,3
V2 = v0 ( t = 8 ) = E ⋅ e −T / 2τ = 3 V
→
−
T
V 
= ln  2 
2τ
E
T
16 ⋅ 10 −6
τ =−
=−
= 11,54 ⋅ 10 −6 s
2 ln (V2 / E )
2 ln (1 / 2 )
da cui
essendo τ =
L = τ ⋅ R = 11,54 ⋅ 10 −6 ⋅ 32 ⋅ 10 3 = 184,64 ⋅ 10 −3 H = 0 ,184 mH
L
R