Problema
Dato un qualsiasi triangolo isoscele ABC con base AB e angolo ACB=a, trovare la
percentuale dell'area coperta dai cerchi inscritti convergenti in C.
Soluzione
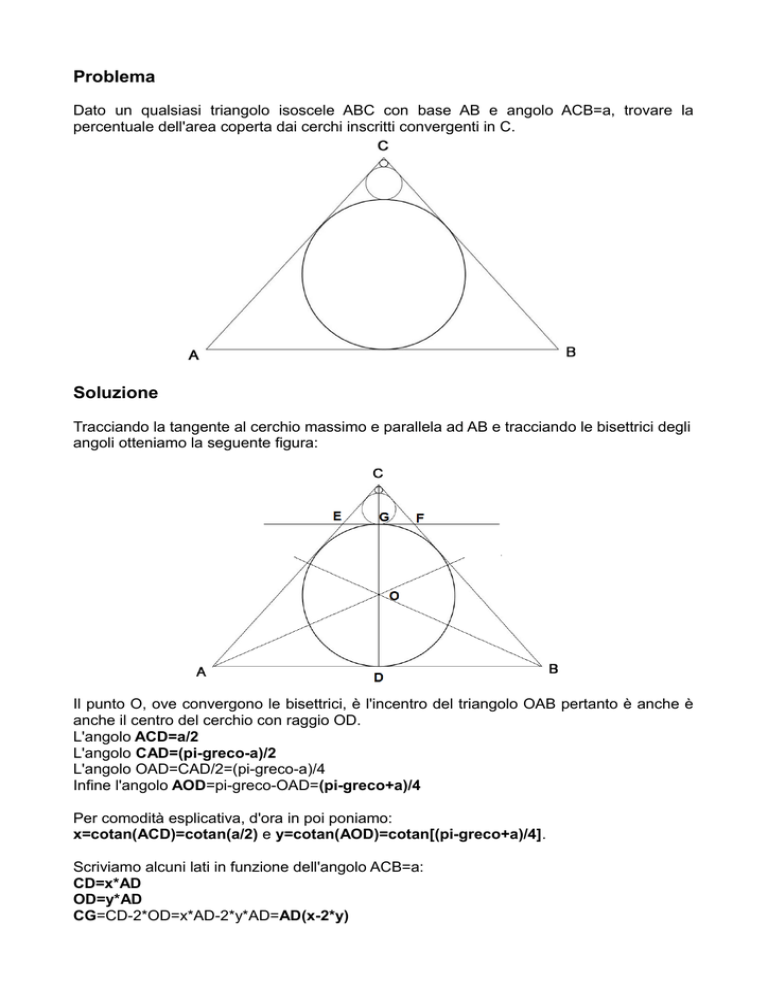
Tracciando la tangente al cerchio massimo e parallela ad AB e tracciando le bisettrici degli
angoli otteniamo la seguente figura:
Il punto O, ove convergono le bisettrici, è l'incentro del triangolo OAB pertanto è anche è
anche il centro del cerchio con raggio OD.
L'angolo ACD=a/2
L'angolo CAD=(pi-greco-a)/2
L'angolo OAD=CAD/2=(pi-greco-a)/4
Infine l'angolo AOD=pi-greco-OAD=(pi-greco+a)/4
Per comodità esplicativa, d'ora in poi poniamo:
x=cotan(ACD)=cotan(a/2) e y=cotan(AOD)=cotan[(pi-greco+a)/4].
Scriviamo alcuni lati in funzione dell'angolo ACB=a:
CD=x*AD
OD=y*AD
CG=CD-2*OD=x*AD-2*y*AD=AD(x-2*y)
Infine, poiché i triangoli ABC e ECF hanno i medesimi angoli, i lati sono proporzionali:
pertanto dalla proporzione CG:EF=CD:AB ricaviamo EF.
EF=CG*AB/CD=[AD(x-2y)*2*AD]/x*AD=[2*AD(x-2y)]/x
Definiamo con T1 l'area del triangolo ABC, con T 2 l'area del triangolo ECF, con T 3 il
successivo triangolo, con Ck l'area del k-esimo trinagolo convergente in C...e così via.
Definiamo con C1 l'area del cerchio massimo e con C 2, C3, C4...Ck e così via le aree dei
cerchi convergenti in C.
Il rapporto fra i raggi dei cerchi inscritti e l'altezza dei triangoli convergenti in C dipende
solo dall'ampiezza dell'angolo ACB (infatti OD/CD=x/y): ne deriva che i rapporti C k/Tk sono
costanti per ogni valore 0<a<pi-greco. Di conseguenzalo saranno anche i rapporti:
C1/(T1-T2) = C2/(T2-T3) = C3/(T3-T4) = … = Ck/(Tk-T(k+1))
dove T1-T2 è l'area del trapezio AEFB.
Indichiamo con R il rapporto cercato, ovvero il rapporto fra la somma delle aree di tutti i
cerchi convergenti in C e l'area del triangolo ABC.
Scriviamo: R=Sk(Ck)/T1.
Dove Sk è la sommatoria in k che va da 1 a infinito delle aree Ck.
Moltiplicando ogni elemento Ck per (Tk-T(k+1))/(Tk-T(k+1)) = 1 otteniamo:
R = (1/T1)* Sk [Ck*(Tk-T(k+1))/(Tk-T(k+1))]
Sappiamo che Ck/(Tk-T(k+1)) = C1/(T1-T2) , pertanto possiamo estrarre la costante da Sk:
R = (1/T1)*[C1/(T1-T2)]* Sk (Tk-T(k+1)) = (1/T1)*[C1/(T1-T2)]*[ Sk (Tk)- Sk (T(k+1))]
Dato che Sk (Tk) = T1 + Sk (T(k+1)) la formula si semplica in:
R = C1/(T1-T2) = Ck/(Tk-T(k+1))
Ovvero, R è costante per ogni dato angolo 0<a<pi-greco ed è sempre pari al rapporto fra
l'area del k-esimo cerchio e l'area del k-esimo trapezio.
C1 = pi-greco*OD^2 = pi-greco*y^2*AD^2
T1-T2 = (AB+EF)*GD/2 = (AB+EF)*OD =[4*AD^2*y*(x+y)]/x
R = C1/(T1-T2) = [pi-greco*x*y]/[4*(x-y)]
Sostituendo x e y e passando alle tangenti si ottiene:
Se a = pi-greco/3, allora il triangolo è equilatero e R = 0,6802, ovvero il 68,02%.
Se a = pi-greco/4, allora è un triangolo rettangolo isoscele e R = 0,7256, ovvero il 72,56%.
Per a che tende a zero, R=pi-greco/4
Per a che tende a pi-greco, R=0












