.
A
p.
S.
br
i
Parte Seconda
C
op
yr
ig
ht
©
Es
se
li
Prova di selezione culturale
C
op
yr
ig
ht
©
Es
se
li
br
i
S.
p.
A
.
.
A
p.
S.
MATEMATICA
i
ARITMETICA
br
TEORIA DEGLI INSIEMI
Insieme = gruppo di elementi di cui si può stabilire inequivocabilmente almeno una caratteristica in comune.
se
un insieme si indica con la lettera maiuscola
gli elementi dell’insieme con la lettera minuscola
li
Esempi: le vocali dell’alfabeto italiano costituiscono un insieme;
i libri più interessanti della biblioteca non costituiscono un insieme, perché non lo si
può stabilire con certezza
A = { a, b, c, d, e }
䉴 A = B (uguaglianza): gli insiemi A e B sono uguali
Es
䉴 b ∈ A (appartenenza): l’elemento b appartiene all’insieme A
䉴 b ∉ A (non appartenenza): l’elemento b non appartiene all’insieme A
䉴 A = ∅ : l’insieme A è vuoto
Simboli relativi
agli insiemi
䉴 A ⊂ B : l’insieme A è un sottoinsieme di B
ciò vuol dire che ogni elemento di A appartiene anche a B, ma non viceversa;
es. A è l’insieme delle città della Lombardia, B l’insieme delle città italiane
©
䉴 C = A ∩ B (intersezione): l’insieme C è costituito dagli elementi in comune
tra A e B
ht
䉴 C = A ∪ B (somma): l’insieme C è costituito dalla somma degli insiemi A e B
CORRISPONDENZE TRA INSIEMI
ig
Gli elementi di due differenti insiemi possono essere in relazione tra loro. Questa relazione si
chiama corrispondenza.
op
yr
Es. l’insieme A degli abbonati telefonici e l’insieme B dei numeri telefonici: a ogni abbonato è
abbinato un numero; perciò si dice che A e B sono in corrispondenza.
C
Tipi di corrispondenze
䉴 Univoca
Si ha quando a ogni elemento del primo insieme corrisponde un solo elemento del secondo, ma non viceversa (a un elemento del secondo insieme
possono corrispondere anche più elementi del primo).
䉴 Biunivoca
Si ha quando a ogni elemento del primo insieme corrisponde un solo elemento del secondo insieme e viceversa.
.
A
40
p.
Parte Seconda - Prova di selezione culturale
I NUMERI
br
i
S.
I numeri sono classificati in insiemi, quindi, indicati ognuno con una lettera maiuscola.
Ogni insieme di numeri ha le sue operazioni (addizione, sottrazione etc.) che possono essere di 2 tipi:
• operazione interna
Si ha quando il risultato dell’operazione è un numero che appartiene allo stesso insieme di
partenza.
Es. la somma di due numeri naturali è sempre un numero naturale: 2 + 5 = 7
• operazione non interna
Si ha quando il risultato dell’operazione non è sempre un numero che appartiene allo stesso
insieme.
Es. la sottrazione di due numeri naturali: 4 – 3 = 1 (dà un numero naturale), ma 3 – 4 = –1 (dà
un numero relativo)
li
䉴 Numeri Naturali (N)
Numeri interi positivi, compreso lo zero (0, 1 , 2, 3, 4, 5 etc.)
operazioni interne: addizione, moltiplicazione
se
䉴 Numeri Relativi (Z)
Sono i numeri positivi (Z+) e negativi (Z-)
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5 etc.
operazioni interne: addizione, sottrazione, moltiplicazione, divisione
Es
䉴 Numeri Razionali (Q)
1 1 3
Possono essere indicati o come frazione , , o come parte intera
4 2 4
+ parte decimale (1,5; 0,7; 4,8)
operazioni interne: addizione, sottrazione, moltiplicazione, divisione
Insiemi numerici
©
䉴 Numeri Irrazionali (J)
Non possono essere trasformati in un numero razionale.
Es. ÷2 (dà un valore dalla cifra decimale infinita: 1, 4142135624...)
ht
䉴 Numeri Reali (R)
Sono l’unione tra Q e J. Quindi R = Q ∪ J
ig
Come si vede, gli insiemi numerici sono in relazione fra loro.
Es. N è un sottoinsieme di Z(N ⊂ Z); Z è a sua volta un sottoinsieme di Q(Z ⊂ Q); tutti sono un
sottoinsieme di R.
yr
LE OPERAZIONI CON I NUMERI NATURALI (N)
Interna
C
op
addizione
si
Descrizione
Proprietà
produce la somma fra due numeri chiamati addendi
proprietà commutativa
una somma non cambia se si cambia l’ordine degli
addendi
es. 2 + 18 = 18 + 2
Segue
.
A
41
S.
no
proprietà associativa:
la somma di più addendi non cambia, se a due o più
di essi si sostituisce la loro somma
es. (4 + 7) + 1 = 4 + (7 + 1)
proprietà invariantiva: aggiungendo o togliendo
uno stesso numero sia al minuendo che al sottraendo, la differenza non cambia
es. 5 – 3 = (5 + 2) – (3 + 2)
li
proprietà associativa:
il prodotto di più fattori non cambia, se a due o più
di essi si sostituisce il loro prodotto
es. (4 × 7) × 2 = 4 × (7 × 2)
se
si
proprietà commutativa:
il prodotto non cambia se si inverte l’ordine dei fattori
es. 2 × 3 = 3 × 2
proprietà distributiva: per moltiplicare una somma
per un numero, si possono moltiplicare per quel numero i singoli addendi e sommare i prodotti ottenuti
es. (3 + 5 + 2) × 7 = (3 × 7) + (5 × 7) + (2 × 7)
Es
moltiplicazione
calcola il prodotto tra due numeri
detti fattori;
il prodotto è la
somma di tanti
addendi uguali al
primo quante
sono le unità del
secondo
es. 2 × 3 = 2 + 2 + 2
br
i
sottrazione
produce la differenza tra due numeri il primo dei
quali si chiama
minuendo e il secondo sottraendo
p.
Matematica - Aritmetica
©
no
yr
ig
ht
divisione
calcola il quoziente tra due numeri detti il primo
dividendo e il secondo divisore;
il quoziente è il
numero che moltiplicato per il divisore dà come
prodotto il dividendo
proprietà distributiva rispetto all’addizione:
per dividere una somma per un numero, si può anche dividere per quel numero i singoli addendi e sommare i quozienti
es. (4 + 8) : 2 = (4 : 2) + (8 : 2)
proprietà distributiva rispetto alla moltiplicazione:
per dividere un prodotto per un numero si può dividere uno solo dei fattori per quel numero e moltiplicare il quoziente per gli altri fattori
es. (5 × 2 × 6) : 3 = 5 × 2 × (6 : 3)
proprietà invariantiva:
il quoziente di due numeri non cambia se si moltiplica o si divide per uno stesso numero ciascuno di essi
es. 4 : 2 = (4 × 3) : (2 × 3)
C
op
Osservazioni
— moltiplicando un numero per 1 si ottiene lo stesso numero: 3 × 1 = 3
— moltiplicando un numero per 0 si ottiene 0 : 3 × 0 = 0
— nella divisione, quando non esiste un quoziente appartenente ai numeri naturali, si produce il
quoziente approssimato più il resto; es. 52 : 10 = 50 (quoziente appr.) + 2 (resto)
— nelle espressioni con più operazioni, ove non indicato dalle parentesi, si effettuano prima le
moltiplicazioni e le divisioni: 4 × 5 + 6 : 2 = (4 × 5) + (6 : 2) = 20 + 3 = 23
.
A
42
p.
Parte Seconda - Prova di selezione culturale
LE POTENZE
䉴
䉴 42 = 4 × 4 = 16
䉴
il 4 si chiama base
il 16 è la potenza
i
il 2 si chiama esponente
l’operazione si chiama “elevazione a potenza”
S.
Potenza di un numero = prodotto di più fattori uguali a quel numero
br
L’esponente indica quante volte la base deve essere moltiplicata per se stessa per ottenere la
potenza.
Es
se
li
Nota
Le potenze con esponente 2 si chiamano “elevazione al quadrato”; perciò 32 si legge “tre al
quadrato”
Le potenze con esponente 3 si chiamano “elevazione al cubo”; perciò 43 si legge “quattro al
cubo”
In tutti gli altri casi si usa il numero cardinale relativo: 25 = “due alla quinta”, 34 = “tre alla
quarta” etc.
Qualunque potenza con esponente 1 è uguale alla base: 71 = 7, 81 = 8 etc.
Qualunque potenza con esponente 0 è uguale a 1: 30 = 1, 4 0 = 1 etc.
Le potenze con base 10 sono semplici da calcolare: corrispondono a una cifra con tanti zeri
quanti indica l’esponente es. 102 = 100, 106 = 1.000.000 etc.
䉴 il prodotto di due o più potenze aventi la medesima base è uguale a un’al
tra potenza della stessa base che ha per esponente la somma degli esponenti.
Es. 23 × 22 = 2 3 + 2 = 25
Operazioni con
le potenze
ht
©
䉴 il quoziente di due potenze aventi la medesima base è uguale a un’altra
potenza della stessa base che ha per esponente la differenza degli esponenti.
Es. 25 : 23 = 25 – 3 = 22
䉴 la potenza di una potenza è un’altra potenza della stessa base che ha per
esponente il prodotto degli esponenti. es. (23)2 = 23 × 2 = 26
ig
䉴 per elevare a potenza un prodotto di più fattori basta elevare a potenza i
singoli fattori. Es. (3 × 2)2 = 32 × 22
yr
䉴 per elevare a potenza un quoziente basta elevare a quella potenza il dividendo ed il divisore. Es. (12 : 4)2 = 12 2 : 42
LA RADICE QUADRATA E LA RADICE CUBICA
op
Estrazione della radice quadrata = operazione inversa dell’elevazione al quadrato
C
quindi 4 = 2 perché 22 = 4.
Il 4 all’interno della radice si dice radicando ed il 2 si dice radice quadrata.
.
A
43
quindi 3 9 = 3 perché 33 = 9.
Il 9 all’interno della radice si dice radicando ed il 3 si dice radice cubica
S.
Estrazione della radice cubica = operazione inversa dell’elevazione al cubo
p.
Matematica - Aritmetica
br
i
Nota
L’estrazione della radice non è sempre possibile nell’insieme dei numeri naturali; vale a dire che
è un’operazione non interna all’insieme N.
È possibile soltanto con numeri che vengono rispettivamente chiamati:
— quadrati perfetti: numeri N la cui radice quadrata è a sua volta un numero N
— cubi perfetti: numeri N la cui radice cubica è a sua volta un numero N
ht
15
se
n2
1
4
9
16
25
36
49
64
81
100
121
144
169
196
Es
©
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
li
Nella seguente tabella, come esempio, riportiamo i primi quindici numeri naturali con i rispettivi
quadrati e cubi. La seconda e la terza colonna contengono perciò i primi quadrati perfetti e
cubi perfetti.
225
n3
1
8
27
64
125
216
343
512
729
1.000
1.331
1.728
2.197
2.744
3.375
ig
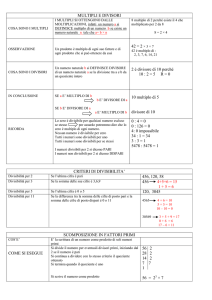
LA DIVISIBILITÀ
yr
Come detto, la divisione non è sempre possibile nell’insieme N. Per capire quando è possibile
bisogna partire dal concetto di multiplo.
Multiplo: un numero è multiplo di un altro se è il prodotto di questo numero per un terzo.
Es. 52 è multiplo di 26 perché 52 = 26 × 2
C
op
quindi: la divisione tra due numeri N è possibile solo se il dividendo è multiplo del divisore
Es. è possibile perché è un multiplo di (infatti )
Esistono alcuni metodi per calcolare rapidamente se un numero è divisibile per un altro
.
A
44
p.
Parte Seconda - Prova di selezione culturale
䉴 sono divisibili per 2:
tutti i numeri pari
S.
䉴 sono divisibili per 3:
tutti i numeri la somma delle cui cifre dà un multiplo di 3
es. 861 è divisibile per 3 perché 8 + 6 + 1 = 15 che è un multiplo di 3
br
i
䉴 sono divisibili per 4:
tutti i numeri le cui ultime due cifre sono 0 o un multiplo di 4
es. 100 è divisibile per 4 perché le ultime due cifre sono “00”; 112 è divisibile
anch’esso per 4 perché le ultime due cifre sono “12”, un multiplo di 4
䉴 sono divisibili per 5:
tutti i numeri che terminano con la cifra 0 o 5.
es. lo sono 10, 25, 140, 155 etc.
li
䉴 sono divisibili per 9:
tutti i numeri la somma delle cui cifre dà un multiplo di 9
es. 4.455 è divisibile per 9 perché 4 + 4 + 5 + 5 = 18 che è un multiplo di 9
se
Criteri di divisibilità
䉴 sono divisibili per 10:
tutti i numeri che terminano con uno o più 0
es. 10, 20, 300, 1.000 etc.
©
Es
䉴 sono divisibili per 11:
si esegue la seguente operazione
— si sommano le cifre di posto pari
— si sommano le cifre di posto dispari
— si fa la sottrazione fra il maggiore e il minore dei numeri ottenuti
— se il risultato è un multiplo di 11, il numero di partenza è divisibile
es. 60.808 è divisibile per 11 perché (6+8+8) – (0 + 0) = 22 – 0 = 22, che è
multiplo di 11
ig
I NUMERI PRIMI
ht
䉴 sono divisibili per 25:
tutti i numeri le cui ultime due cifre sono “00” o un numero divisibile per 25
es. 50, 125, 150, 175 etc.
Numero primo: numero che può essere diviso soltanto per se stesso o per 1
es. 1, 7, 23 etc.
yr
I numeri primi sono infiniti e si desumono da una speciale tabella. Di seguito riportiamo soltanto
i primi quindici fra essi.
C
op
Numeri
Primi
1
2
3
5
7
11
13
17
19
23
29
31
37
41
43
etc.
.
A
45
p.
Matematica - Aritmetica
Ne consegue che l’insieme N può essere diviso in 2 sottoinsiemi:
Sottoinsiemi
dell’insieme N
S.
䉴 Numeri primi
possono essere divisi soltanto per sé o per 1
i
䉴 Numeri composti
sono il risultato della moltiplicazione fra più numeri primi
es. (6 è un numero composto perché 6 = 3 × 2)
br
Ogni numero composto può perciò essere scomposto in fattori primi.
SCOMPOSIZIONE DI UN NUMERO IN FATTORI PRIMI
li
Si effettua dividendo il numero per il più piccolo numero primo che sia suo divisore ed effettuando la stessa operazione al risultato finché non si ottiene 1. La scomposizione sarà il prodotto di
tutti i numeri primi adoperati come divisori.
se
Es. scomponiamo 855
Es
855 è multiplo di 3 perché 8 + 5 + 5 = 18; quindi 855 : 3 = 285
285 è multiplo di 3 perché 2 + 8 + 5 = 18; quindi 285 : 3 = 95
95 è multiplo di 5 quindi 95 : 5 = 19
19 è un numero primo quindi può essere diviso solo per se stesso: 19 : 19 = 1
Per ottenere 1 abbiamo usato i divisori 3, 3, 5 e 19; quindi diremo che la scomposizione in fattori
primi di 855 è: 32 × 5 × 19
©
MASSIMO COMUNE DIVISORE (M.C.D.)
ht
Il massimo comune divisore fra due numeri N è il maggiore tra i divisori che i due numeri
hanno in comune.
Es. consideriamo gli insiemi dei divisori di 24 e 40:
ig
D24 = {1, 2, 3, 4, 6, 8, 12, 24}
D40 = {1, 2, 4, 5, 8, 10, 20, 40}
I due numeri hanno in comune i divisori 1, 2, 4, 8. Perciò 8 è il M.C.D.
yr
Per calcolare il M.C.D. si utilizza la scomposizione in fattori primi:
C
op
Calcolo del Massimo
Comune Divisore
il M.C.D. di due o più numeri si trova scomponendo i numeri in fattori primi e
moltiplicando fra loro i fattori comuni, presi una sola volta con il minimo esponente con cui compaiono nella scomposizione
.
A
46
p.
Parte Seconda - Prova di selezione culturale
Es. troviamo il M.C.D. tra 840 e 900.
i
S.
Scomponiamo i numeri in fattori primi e otteniamo che:
• 840 = 2 3 × 3 × 5 × 7
• 900 = 2 2 × 32 × 52
Adesso moltiplichiamo fra loro i fattori primi che hanno in comune col minimo esponente, quindi 22 × 3 × 5
60 è perciò il M.C.D.
br
MINIMO COMUNE MULTIPLO (m.c.m.)
Es. consideriamo gli insiemi dei multipli di 4 e 10:
se
M4 = {4, 8, 12, 16, 20, 24, 28, etc.}
D40 = {10, 20, 30, 40, 50, 60, etc.}
li
Il minimo comune multiplo fra due o più numeri è il più piccolo fra i multipli che tali numeri
hanno in comune.
Es
Come si vede, il primo multiplo in comune che troviamo è 20. Perciò 20 è il minimo comune
multiplo o m.c.m.
Per calcolare il m.c.m. si utilizza la scomposizione in fattori primi:
il m.c.m. di due o più numeri si trova scomponendo i numeri in fattori primi e
moltiplicando fra loro i fattori comuni e non comuni, presi una sola volta con il
massimo esponente con cui compaiono nella scomposizione
©
Calcolo del minimo
comune multiplo
Es. troviamo il m.c.m. tra 504 e 3.564.
ig
ht
Scomponiamo i numeri in fattori primi e otteniamo che:
• 504 = 2 3 × 32 × 7
• 3.564 = 2 2 × 34 × 11
Adesso moltiplichiamo fra loro tutti i fattori primi col massimo esponente, quindi
23 × 34 × 7 × 11 = 49.896
49.896 è perciò il m.c.m.
yr
Questo vale per i numeri più grandi. Per quelli più piccoli esistono alcuni metodi per un calcolo
rapido.
C
op
Calcolo rapido
del m.c.m.
䉴 Se due numeri sono primi, il m.c.m. è il loro prodotto
quindi il m.c.m. tra 8 e 15 è 8 × 15 = 120
䉴 Dati due o più numeri, se il maggiore di loro è multiplo di tutti gli altri,
è il m.c.m.
quindi il m.c.m. tra 2, 5, 30 è 30