pauli

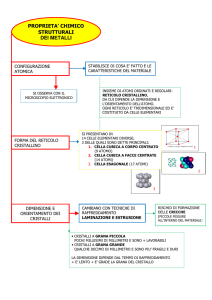
CAP.3 - CLASSIFICAZIONE DEI SOLIDI.
Abbiamo classificato i solidi in base alle loro proprietà di simmetria. Li
classificheremo ora in base alle loro proprietà fisiche determinate dalla
distribuzione degli elettroni di valenza nell'atomo. La coesione del solido è
determinata dalla forza di attrazione elettrostatica tra elettroni e nucleo.
L'energia di coesione o di legame è la differenza tra l'energia del cristallo
(energia cinetica e potenziale) e l'energia degli atomi liberi cioè nel loro stato
fondamentale, T=O K. Essendo l'energia dello stato legato più bassa di quella
nello stato libero, l'energia di legame è negativa. I cristalli più semplici sono i
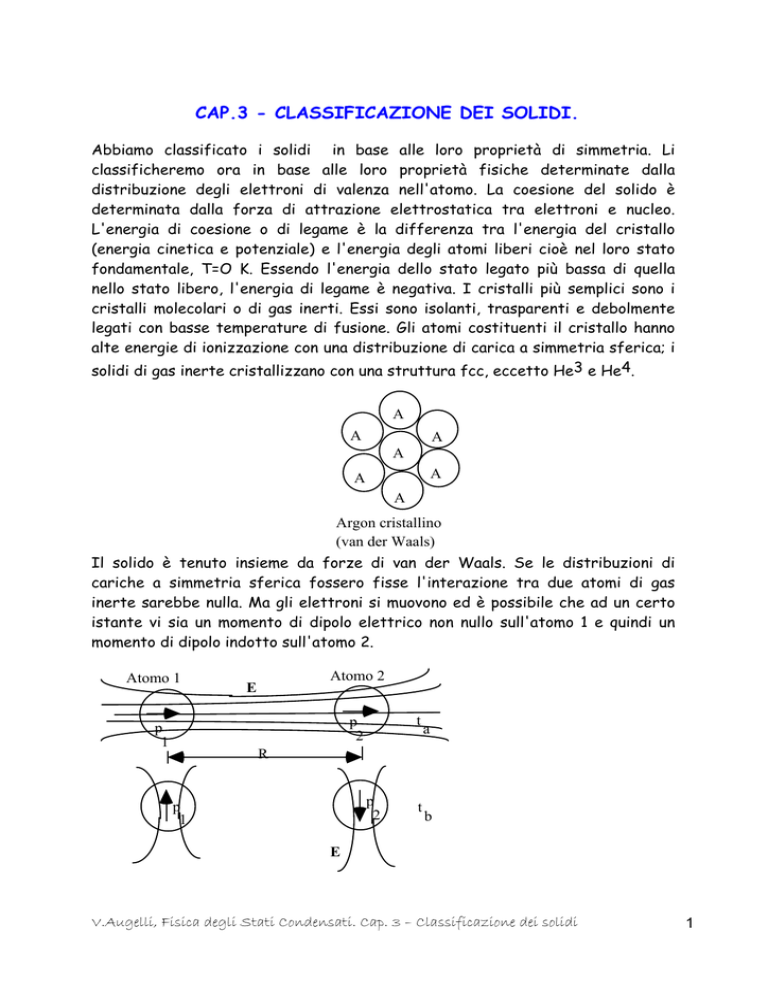
cristalli molecolari o di gas inerti. Essi sono isolanti, trasparenti e debolmente
legati con basse temperature di fusione. Gli atomi costituenti il cristallo hanno
alte energie di ionizzazione con una distribuzione di carica a simmetria sferica; i
solidi di gas inerte cristallizzano con una struttura fcc, eccetto He3 e He4.
A
A
A
A
A
A
A
Argon cristallino
(van der Waals)
Il solido è tenuto insieme da forze di van der Waals. Se le distribuzioni di
cariche a simmetria sferica fossero fisse l'interazione tra due atomi di gas
inerte sarebbe nulla. Ma gli elettroni si muovono ed è possibile che ad un certo
istante vi sia un momento di dipolo elettrico non nullo sull'atomo 1 e quindi un
momento di dipolo indotto sull'atomo 2.
Atomo 1
Atomo 2
E
t
p
2
p
1
a
R
p
2
p
1
t
b
E
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
1
Il campo elettrico prodotto da 1 nella posizione occupata da 2 è
2p 1 / R 3
e il
2p1
dove α è la polarizzabilità elettronica.
R3
2p 1 p 2
4αp 1 2
U (R ) ≈ −
=−
ed è
L'energia potenziale d'interazione è
R3
R6
−6
(interazione di van der Waals o di London o di
attrattiva, pertanto U ∝ R
momento indotto è
p 2 = αE = α
dipolo fluttuante).
Avvicinando due atomi, le distribuzioni di carica si sovrappongono e diventa
importante l'interazione repulsiva (da 5 Å a 0.5 Å). Questa è essenzialmente
dovuta alla tendenza di un elettrone ad occupare stati occupati da un altro
elettrone con conseguente violazione del principio di Pauli. Un potenziale
repulsivo empirico è proporzionale a R-12, per cui l'energia potenziale totale di
due atomi a distanza R è :
⎡⎛ σ ⎞ 12 ⎛ σ ⎞ 6 ⎤
U (R ) = 4ε ⎢⎜ ⎟ − ⎜ ⎟ ⎥ (Lennard-Jones)
⎝ R⎠ ⎦
⎣⎝ R ⎠
La costante ε è una misura della forza dell'interazione ed è il valore di U nel
minimo. Posto dU/dR=0 si ottiene R min = 1.122 σ e per R=Rmin , Umin = -ε ;
inoltre, U=0 per σ=R
6
U/ 4 ε
0
R/ σ
1
Se trascuriamo l'energia cinetica degli atomi di un cristallo di gas inerte,
l'energia di coesione sarà la somma dei potenziali d'interazione tra tutte le
coppie. Se gli atomi sono N:
U tot
⎡ ⎛
⎞ 12
⎛ σ ⎞6⎤
1
σ
⎟ − ∑⎜
⎟ ⎥
= N4 ε ⎢ ∑ ⎜⎜
⎟
⎟
⎜
⎢ j≠ i ⎝ p ij R ⎠
2
j≠i ⎝ p ij R ⎠ ⎥
⎦
⎣
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
2
dove R è la distanza tra primi vicini, 1/2 evita di contare due volte ogni coppia,
p ij R è la distanza tra l'atomo di riferimento i e il generico j, quindi se R
congiunge primi vicini
p ij
1
p ij n
= 12.131
dimostrare che la serie
n=12 si trova
∑ p ij −12
=1. Per un reticolo fcc i primi vicini sono 12 e si può
∑
per n→ ∞ , tende al numero di primi vicini 1; per
e per n=6
j≠ i
∑ p ij −6 = 14.454
e imponendo che
j≠ i
Utot sia minima si trova Ro/σ = 1.09. Sperimentalmente si trova 1.09 per lo
xenon, 1.1 per il kripton, 1.11 per l'argon e 1.14 per il neon. Per R=Ro, valore
all'equilibrio, l'energia di coesione è quindi:
⎡
⎛ σ ⎞ 12
⎛ σ ⎞6⎤
U tot (R o ) = 2 Nε ⎢12.13⎜
⎟ − 14. 45⎜
⎟ ⎥ = −2.15 ⋅ 4N ε
⎢⎣
R
R
⎝ o⎠
⎝ o ⎠ ⎥⎦
L'energia di coesione all'equilibrio, per particella, vale quindi -8.6 ε.
Se si tiene conto della energia cinetica, le correzioni sono tanto più piccole
quanto più pesante è l'atomo di gas inerte.
Cristalli ionici.
Sono costituiti da ioni di segno opposto; il legame ionico deriva dall'interazione
elettrostatica di ioni con cariche opposte. Le strutture sono o di tipo NaCl (fcc)
o di tipo CsCl (bcc). Come nei cristalli di gas inerte, le orbite sono complete e la
distribuzione di carica è sfero-simmetrica con una piccola distorsione nei
cristalli ionici; pertanto, l'interazione è elettrostatica (e2/ro) (5.1 eV nel NaCl).
Cl
+
Na Cl-
Na+ Cl Na+
Cl Na+ Cl
Cloruro di sodio (ionico)
La disposizione degli ioni è tale che l'interazione attrattiva è massima
compatibilmente con la repulsione che si ha tra elettroni di atomi vicini.
L'energia elettrostatica (o di Madelung) derivante dall'interazione coulombiana è
molto maggiore del contributo tipo van der Waals che è solo 1 o 2% del totale. La
parte repulsiva del potenziale, della quale si deve tener conto per evitare il
collasso del cristallo, oltre ad essere espressa con un potenziale di tipo Lennard-
1Quanto
più grande è n tanto meno contribuiscono alla somma i secondi, i terzi vicini, ecc...
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
3
Jones, R-12, può anche esprimersi con un potenziale repulsivo a campo centrale,
−r / ρ
, dove λ è l'intensità dell'interazione e ρ l'estensione.
della forma λe
Supponiamo che l'energia di interazione tra gli ioni i e j si possa scrivere come:
U ij = λ e
−r
ij
/ρ
q2
±
r
ij
L'energia reticolare totale di un cristallo di N molecole o 2N ioni è
U tot =
1
2NU i
2
,
Ui =
∑ U ij
j≠i
se siamo lontani dalla superficie Ui non dipende da i (ione scelto). La Utot è
l'energia necessaria per separare a distanza infinita gli ioni del cristallo. Se R è
la distanza tra primi vicini, r ij = p ij R e se consideriamo l'interazione repulsiva
solo tra primi vicini, si ha:
U tot
dove
α=∑
j≠ i
(± )
p ij
⎛
q2 ⎞
− R /ρ
= NU i = N ⎜ z λ e
−α
⎟
R⎠
⎝
=costante di Madelung, z è il numero di primi vicini.
dUtot/dR=0 fornisce la separazione di equilibrio Ro. Se sono note λ e ρ
(estensione dell'interazione repulsiva) si ottiene:
dU tot
q2
αq 2ρ
1
− R /ρ
2 − R /ρ
= − Nz λ e
+ N α 2 = 0 e quindi R o e
=
dR
ρ
R
zλ
⎛
αq 2 ρ αq 2 ⎞
Nα q 2 ⎛
ρ ⎞
e
U tot (R o ) = N ⎜ z λ
−
⎟
=
−
1
−
⎜
⎟;
2
z
λ
R
R
R
R
⎝
⎝
o
o ⎠
o
o ⎠
2
N αq
−
è noto come energia di Madelung. Si trova che ρ/Ro≅ 0.1, per cui
Ro
o
l'interazione repulsiva è ripida con una breve estensione e l'energia di coesione è
dominata dal contributo di Madelung.
Calcoliamo la costante di Madelung, α , nel caso di una catena infinita di ioni di
carica alternata.
+
-
+
-
+
-
R
Ione di riferimento
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
4
eV
E repulsiva
0
E totale
3
R(10
- 5
-8
cm)
E coulombiana
α è definita come α =
∑'
j
±
p ij
oppure come
α
±
= ∑'
R
rj
j
essendo
rj
la distanza
dello ione j da quello di riferimento. Se prendiamo lo ione negativo in figura come
riferimento avremo:
ovvero
α
⎡1
1
1
1
⎤
= 2⎢ −
+
−
+ ......⎥
⎣ R 2 R 3R 4R
⎦
R
⎡ 1 1 1
⎤
α = 2 ⎢1 − + − + ......⎥
⎣ 2 3 4
⎦
il fattore 2 tiene conto che vi sono due ioni alla stessa distanza, uno a destra e
l'altro a sinistra. Se si tiene conto dello sviluppo
si ha:
x2 x3 x4
log(1 + x) = x −
+
−
+ .....
2
3
4
α = 2 log 2 . In tre dimensioni la convergenza della serie dipende dalla
disposizione degli ioni; generalmente essa è debole come si può vedere, per
esempio, per la struttura NaCl. In tal caso si hanno 6 ioni positivi primi vicini, 12
ioni negativi a distanza 2 , 8 ioni positivi a distanza 3 , 6 ioni negativi secondi
vicini (p=2), ecc., per cui
α=
e la convergenza è debole.
6 12
8 6
−
+
− + ........
1
2
3 2
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
5
Cristalli covalenti.
Il legame è forte, omopolare, dovuto alla sovrapposizione delle funzioni d'onda di
due elettroni, uno per atomo, che partecipano al legame. Gli spin sono
antiparalleli e gli elettroni sono parzialmente localizzati nella regione tra i due
atomi. Il principio di Pauli dà luogo ad un'interazione repulsiva se gli atomi hanno
orbite complete; viceversa, la sovrapposizione elettronica si può effettuare. Il
legame dell'idrogeno molecolare è covalente. Prototipo di questa struttura è il
diamante. I cristalli covalenti puri non sono conduttori; hanno coesione e durezza
molto elevate.
C
C
C
C
Diamante (covalente)
C
Cristalli metallici.
I metalli hanno una grande conducibilità elettrica e gli elettroni che si muovono
quasi liberamente sono chiamati elettroni di conduzione. L'interazione tra gli
elettroni di conduzione e gli ioni dà un contributo più o meno grande all'energia
di legame. La coesione è assicurata dall'interazione tra ioni e elettroni di
conduzione.
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
6
Na+
Na+
Na+
Na+
Na+
Sodio metallico
Cristalli con legame idrogeno.
L'idrogeno avendo un solo elettrone dovrebbe formare legame covalente con un
altro atomo. Invece, con atomi abbastanza elettronegativi (F, O, N) la sua nuvola
elettronica forma un legame quasi covalente con tali atomi elettronegativi e, se
nelle vicinanze si trova un atomo carico negativamente, forma legame di tipo
elettrostatico per cui si forma il tipico legame a ponte.
F-
F
-
legame idrogeno
+
H
V.Augelli, Fisica degli Stati Condensati. Cap. 3 – Classificazione dei solidi
7