Altezze, mediane, bisettrici e assi: che cosa hanno di speciale

Stefania Pozio
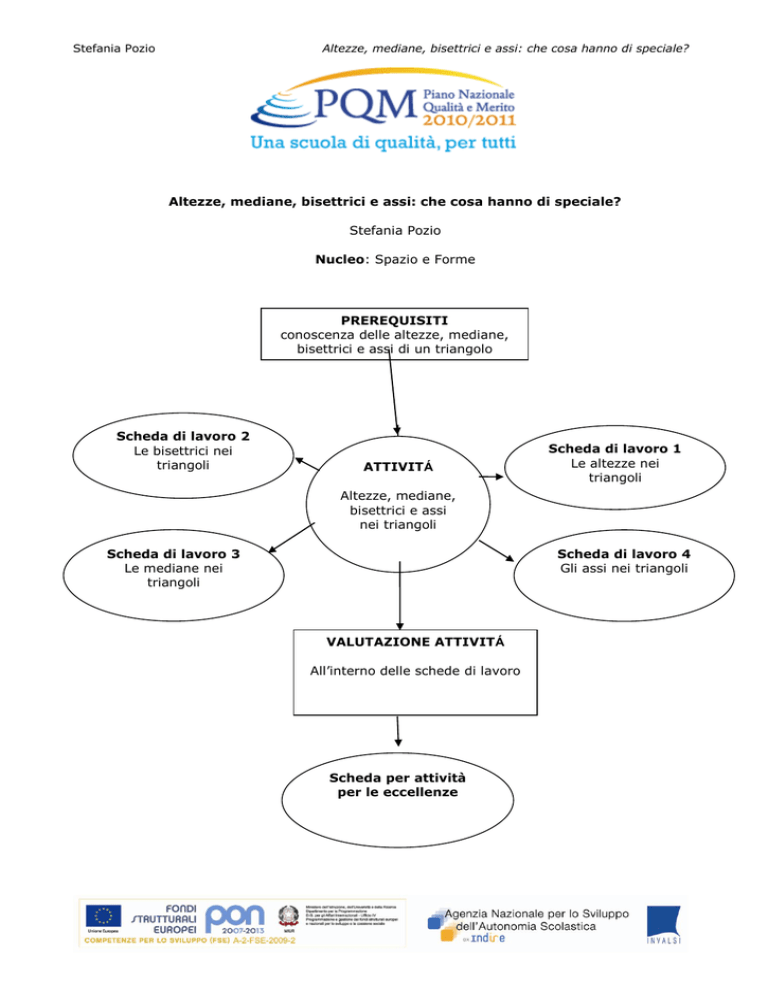
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Stefania Pozio
Nucleo: Spazio e Forme
PREREQUISITI
conoscenza delle altezze, mediane,
bisettrici e assi di un triangolo
Scheda di lavoro 2
Le bisettrici nei
triangoli
ATTIVITÁ
Scheda di lavoro 1
Le altezze nei
triangoli
Altezze, mediane,
bisettrici e assi
nei triangoli
Scheda di lavoro 3
Le mediane nei
triangoli
Scheda di lavoro 4
Gli assi nei triangoli
VALUTAZIONE ATTIVITÁ
All’interno delle schede di lavoro
Scheda per attività
per le eccellenze
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Introduzione
Tematica: Altezze, mediane, bisettrici e assi di un triangolo.
Finalità e obiettivi di apprendimento: l’obiettivo di questa attività è quello di far lavorare
gli studenti su modelli di triangoli costruiti in carta o in cartoncino, far localizzare altezze,
mediane, bisettrici e assi senza l’uso di riga e/o squadra, ma sfruttando le loro proprietà, e,
infine, insegnare loro ad utilizzare il software Geogebra che permette di avere una visione
dinamica delle proprietà di questi segmenti particolari.
Metodologia: si tratta sempre di attività laboratoriali da svolgersi in piccoli gruppi o
singolarmente. L’unità è divisa in quattro diverse attività. Per ciascuna di esse è stata messa a
punto una scheda rivolta all’insegnante in cui è spiegato come far svolgere agli studenti tale
attività. Ogni attività è divisa in due fasi: nella prima fase si lavora con le mani per costruire
triangoli di diversi tipi di carta o cartoncino e per individuare una volta le altezze, un’altra le
bisettrici, un’altra ancora le mediane e infine, gli assi. Nella seconda parte si lavora al
computer utilizzando Geogebra.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Descrizione dell’attività
Condizione, problema o stimolo da cui nasce l'attività
In prima media, quando si cominciano ad analizzare i triangoli e a studiarne le loro proprietà,
si affronta anche l’argomento che riguarda la localizzazione e costruzione delle altezze,
bisettrici, mediane e assi di un triangolo. Molto spesso questo argomento si limita a far
disegnare agli studenti i tre diversi tipi di triangoli (acutangoli, rettangoli ottusangoli) e a far
disegnare questi segmenti “speciali” con l’uso della riga e della squadra, ma, come sostiene la
Castelnuovo:
1) il disegno non suggerisce dei problemi perché offre un numero finito di casi (…);
2) non conduce all’osservazione per il fatto che è statico;
3) non può fornire un’immagine reale di una situazione spaziale.
(Didattica della matematica pag. 85-86)
Ecco dunque da che cosa è nata l’esigenza di un’attività pratica che riguardava questo
argomento.
Inoltre, ormai l’era dell’informatica mette a disposizione gratuitamente dei software come
Geogebra che hanno delle enormi potenzialità per far comprendere meglio determinati
concetti, ma che ancora sono sotto utilizzati sia dagli insegnanti, ma soprattutto dagli studenti.
Prerequisiti richiesti ai ragazzi per svolgere l’attività
Per tutte le attività è necessario che gli studenti sappiano cosa siano le altezze, le mediane, le
bisettrici e gli assi di un triangolo. È sufficiente che ne conoscano la definizione, ma non è
necessario che abbiano già provato a disegnarli con la riga e/o la squadra.
Strumenti forniti agli allievi
Per tutte le attività proposte gli studenti devono avere con loro un righello, un paio di forbici,
del cartoncino (Attività 1 e Attività 3) o dei fogli di carta di tipo A4 (Attività 2 e Attività 4). Per
l’Attività 1 è necessario un filo a piombo (è sufficiente un filo ogni 2-3 studenti). Per l’Attività 3
è necessario un ago con del filo per cucire colorato, uno per ogni studente.
Inoltre, per poter realizzare la seconda fase di ciascuna attività sono necessari i computer,
possibilmente uno per studente. Necessario, ma non indispensabile, un computer per
l’insegnante collegato ad un videoproiettore, in modo che gli studenti possano più facilmente
seguire le istruzioni.
Organizzazione della classe e metodologia
Tutte le attività dovrebbero essere svolte singolarmente, o al massimo in coppia, in modo da
dare a tutti la possibilità di svolgere un’attività pratica. L’insegnante deve coordinare il lavoro e
dare agli studenti le istruzioni necessarie per svolgere il lavoro in modo corretto. Dovrebbe
cercare di controllare che gli studenti lavorino con precisione, eventualmente invitarli a rifare il
lavoro nel caso fosse stato fatto in modo troppo approssimativo. Al termine di ogni fase è
necessario fermarsi per far emergere dagli studenti tutte le possibili osservazioni e anche
uguaglianze e differenze rispetto a ciò che è emerso nell’attività precedente.
Alla fine si potrebbe far costruire agli studenti un quadro sinottico del seguente tipo che
riassume un po’ tutte le loro osservazioni:
Stefania Pozio
Nome
Definizione
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Punto d’incontro
Nome
Caratteristiche
particolari
Interno
(tipo di
triangolo)
Sì (triangolo
acutangolo)
Esterno (tipo
di triangolo)
Altezza
Perpendicolare
dal vertice al
lato opposto
Ortocentro
Bisettrice
Segmento che
divide a metà
ciascun angolo
del triangolo
Incentro
Sempre
Mai
Mediana
Segmento che,
partendo da un
vertice, arriva
alla metà del
lato opposto.
Perpendicolare
a un lato nel
punto medio
Baricentro
Sempre
Mai
Circocentro
Sì (triangolo
acutangolo)
Sì (triangolo
ottusangolo)
Asse
Sì (triangolo
ottusangolo)
Nel triangolo rettangolo
l’ortocentro coincide con
il vertice dell’angolo
retto.
L’incentro rappresenta il
centro della
circonferenza inscritta
nel triangolo.
È equidistante dai lati
del triangolo.
È il punto di equilibrio
del triangolo.
Divide la mediana in due
parti di cui una il doppio
dell’altra.
Nel triangolo rettangolo
il circocentro coincide
con il punto medio
dell’ipotenusa.
Il circocentro
rappresenta il centro
della circonferenza
circoscritta al triangolo.
È equidistante dai
vertici.
Per quanto riguarda la seconda fase di ciascun attività, quella relativa al lavoro al computer,
ciascuna meta scheda riporta le istruzioni che è necessario seguire per le diverse costruzioni.
Sarebbe utile se il docente potesse avere a disposizione un computer collegato ad un
videoproiettore su cui proiettare di volta in volta le diverse schermate riportate sulla meta
scheda per facilitare gli studenti nella comprensione delle istruzioni.
Fasi e tempi
L’unità comprende 4 diverse attività articolate, ciascuna, in due fasi dello stesso lavoro
(l’Attività 4 è suddivisa in 3 fasi). Le attività non devono necessariamente essere svolte
nell’ordine in cui sono state numerate. Tutta l’unità dovrebbe essere svolta nell’arco di quattro
settimane, un’attività a settimana. È meglio mantenere questo ritmo in modo da non far
passare troppo tempo tra un’attività e l’altra e, nello stesso tempo, in modo da dare il tempo
agli studenti di riflettere sugli stimoli forniti. I tempi di svolgimento sono stati stimati uguali
per tutte le attività, anche se, ovviamente, la fase 2, quella che riguarda il lavoro al computer,
richiederà, man mano che le attività vengono svolte, sempre meno tempo nello svolgimento in
quanto gli studenti dovrebbero diventare sempre più “esperti” nel lavorare con Geogebra.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività 1
Le altezze nei triangoli
Tipologia: attività laboratoriale con costruzione di modelli in cartoncino di triangoli di diverso
tipo e relativa individuazione delle altezze, mediane, bisettrici e assi.
Obiettivo didattico: lo scopo di questa attività è di far visualizzare concretamente le altezze,
mediane, bisettrici e assi perché, come afferma la Castelnuovo: “più tempo i nostri ragazzi
avranno dato allo studio del concreto, quanto più tempo avranno perduto nell’osservare, tanto
meglio passeranno dopo alla comprensione delle forme astratte”.
(Didattica della matematica p.75)
Tempo: 3 ore (1 ora + 2 ore)
Fase 1
A ogni alunno fate disegnare e ritagliare su un
cartoncino (va bene il cartoncino delle scatole
dei Corn Flakes) tre triangoli, uno acutangolo,
uno rettangolo e uno ottusangolo (Foto 1).
Costruite un filo a piombo utilizzando del filo da
cucire colorato e un dado di acciaio.
Le dimensioni sono indicative. È meglio che
ciascun alunno disegni un triangolo diverso dai
suoi compagni in modo da avere una maggiore
quantità di esempi e poter quindi effettuare
delle generalizzazioni. I triangoli devono essere
abbastanza grandi, con lati maggiori di 10-12
cm.
Foto 1: i triangoli
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Dividete gli alunni a coppie. Fate prendere il triangolo
acutangolo. Uno studente poggia il triangolo su un lato
e fa passare il filo a piombo per il vertice opposto (vedi
Foto 2), l’altro, con una matita, segna, sul triangolo, il
punto in cui il filo a piombo tocca il lato. Poi, con il
righello, traccia l’altezza unendo il punto trovato con il
vertice opposto.
Fate ripetere lo stesso procedimento per gli altri due lati
(Foto 3).
In questo modo dovrebbero aver trovato l’ortocentro.
Foto 2: la costruzione della prima altezza
Foto 3: la costruzione della seconda e terza altezza
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Ora fate ripetere lo stesso procedimento con il triangolo rettangolo. Gli
studenti dovrebbero osservare subito che il filo a piombo coincide con i
cateti e quindi i cateti rappresentano due delle tre altezze. L’ortocentro
si trova in corrispondenza del vertice dell’angolo retto (Foto 4).
Foto 4: le altezze nel triangolo rettangolo
Foto 5: le altezze nel triangolo ottusangolo
Fate ripetere lo stesso procedimento con il triangolo ottusangolo. Gli studenti vedranno
immediatamente che due delle tre altezze non cadono all’interno del triangolo e quindi
l’ortocentro dovrà trovarsi necessariamente fuori dal triangolo (Foto 5). Per far visualizzare
l’ortocentro in un triangolo ottusangolo, fate disegnare a ciascun alunno un triangolo
ottusangolo su un foglio e, con l’aiuto di riga e squadra, fate individuare l’ortocentro.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fase 2
In questa seconda fase, la costruzione delle altezze viene fatta utilizzando Geogebra. Questo
software
si
può
scaricare
gratuitamente
da
Internet.
Andate
all’indirizzo
http://geogebra.softonic.it/ e poi cliccate su Download.
http://geogebra.softonic.it/
Quando aprite Geogebra vi appare il seguente foglio.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Se cliccate su Visualizza avete la possibilità di far apparire (o sparire) sia gli assi che la griglia.
Per costruire il triangolo, cliccate con il tasto sinistro
del mouse sull’angolino in basso a destra del
riquadro indicato dalla freccia rossa e poi su
Poligono.
Individuate i vertici del triangolo cliccando
sulla griglia con il tasto sinistro del mouse
e poi nuovamente sul vertice iniziale.
Seguite sempre le istruzioni che appaiono
in alto a destra (riquadro rosso).
Ora dovete tracciare le altezze.
Cliccate con il tasto sinistro del
mouse sull’angolino in basso a destra
del riquadro indicato dalla freccia e
poi su Retta perpendicolare. Seguite
le istruzioni (cliccate sul vertice e sul
lato opposto e vi apparirà la
perpendicolare).
Una volta tracciate le tre altezze,
per trovare l’ortocentro dovete
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
cliccare sul riquadro indicato dalla freccia rossa e poi su Intersezione di due punti. A questo
punto, vi posizionate sull’ortocentro e vi cliccate sopra, sempre con il tasto sinistro del mouse.
Vi si apre questa piccola finestrella. Si deve cliccare una volta su Retta d e poi su Retta e
E a questo punto appare il punto D (ortocentro).
Cliccate sul primo riquadro e poi su
Muovi (freccia rossa). Spostatevi
con il mouse sul punto C (o sul
punto A o sul punto B) e, tenendo
premuto il tasto sinistro del mouse
spostate il vertice.
Ovviamente via via che trascinate il
vertice, l’ortocentro si sposta e si
avvicina sempre più all’angolo la
cui ampiezza è vicino a 90° per
arrivare sul vertice dell’angolo retto
nel triangolo rettangolo e poi uscire
fuori nel triangolo ottusangolo.
Discutetene con i vostri studenti.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività 2
Le bisettrici nei triangoli
Tipologia: attività laboratoriale con costruzione di modelli in carta di triangoli di diverso tipo e
relativa individuazione delle bisettrici.
Obiettivo didattico: lo scopo di questa attività è di far costruire e visualizzare concretamente
le bisettrici perché, come afferma la Castelnuovo: “più tempo i nostri ragazzi avranno dato allo
studio del concreto, quanto più tempo avranno perduto nell’osservare, tanto meglio
passeranno dopo alla comprensione delle forme astratte”.
(Didattica della matematica p.75)
Tempo: 3 ore (1 ora + 2 ore)
Fase 1
Fate disegnare e ritagliare a ogni alunno
tre triangoli di carta, uno acutangolo, uno
rettangolo e uno ottusangolo (Foto 1).
Possono anche essere uguali a quelli
costruiti nell’Attività 1.
Anche in questo caso è meglio che ciascun
alunno disegni un triangolo diverso dai
suoi compagni in modo da avere una
maggiore quantità di esempi e poter
quindi effettuare delle generalizzazioni.
Foto 1: i triangoli
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Prendete il primo triangolo (nella Foto 2 è il
triangolo ottusangolo) e dividete manualmente
un angolo perfettamente a metà, piegando il
triangolo in due parti uguali in corrispondenza
del vertice, in modo che due lati combacino.
Ripetete lo stesso procedimento per gli altri
due angoli (Foto 3).
Foto 2: la costruzione delle bisettrici
Bisettrice
3
Incentro
Bisettrice
2
Bisettrice 1
Foto 3: l’incentro nel triangolo ottusangolo
Una volta terminata questa operazione,
che cosa potete far notare agli studenti?
Anche le bisettrici si incontrano tutte in
un unico punto: l’incentro (Foto 3).
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Bisettrice 3
Incentro
Fate ripetere lo stesso procedimento sul
triangolo acutangolo (Foto 4).
Bisettrice 1
Bisettrice 2
Foto 4: l’incentro nel triangolo acutangolo
Incentro
Bisettrice 3
Fate ripetere lo stesso procedimento sul
triangolo rettangolo (Foto 5).
Bisettrice 2
Bisettrice 1
Foto 5: l’incentro nel triangolo rettangolo
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Mettete vicini i tre triangoli piegati.
Che cosa dovete far notare agli studenti? Che
l’incentro è sempre interno ai triangoli, al
contrario dell’ortocentro (Foto 6).
Foto 6: i tre triangoli piegati
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fase 2
In questa seconda fase, la costruzione delle bisettrici viene fatta utilizzando Geogebra.
Per l’apertura del file, seguite le istruzioni fornite all’inizio della Fase 2 dell’Attività 1.
Costruite (e fate costruire ai vostri
studenti) un triangolo qualsiasi oppure
uguale a quello da cui siete partiti per
tracciare le altezze, partendo dal riquadro
Poligono.
Ora costruite le bisettrici. Cliccate con il
tasto sinistro del mouse sull’angolino in
basso a destra del riquadro indicato dalla
freccia e poi su Bisettrici. Cliccate, con il
tasto sinistro del mouse, sul vertice C, poi
sul vertice A e infine sul vertice B per
ottenere la bisettrice dell’angolo A.
Successivamente cliccate sul vertice A, poi
sul vertice B e infine sul vertice C per
ottenere la bisettrice dell’angolo B e così
via.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Una volta trovate le tre bisettrici, per
poter individuare l’incentro dovete
cliccare sul riquadro Intersezione tra due
punti. Spostatevi sull’incentro e vi
apparirà il solito piccolo riquadro.
Cliccate prima su Retta d e
poi su Retta e e così vi
apparirà
il
punto
che
rappresenta l’incentro.
Ma le rette che Geogebra ha tracciato sono veramente le bisettrici degli angoli in A, B e C?
Misuriamo con Geogebra ogni metà angolo e verifichiamo se sono uguali.
Cliccate sul riquadro indicato
dalla freccia rossa e poi su
Angolo. Seguite le istruzioni.
Attenzione, se volete misurare
l’angolo
convesso,
dovete
cliccare sui tre punti in senso
orario.
Ad
esempio
per
misurare l’angolo DAC dovete
cliccare in questo ordine:
prima sul punto D, poi su A e
poi su C. Se cliccate nell’ordine
inverso, Geogebra restituisce
la misura del corrispondente
angolo concavo.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Osservate i valori delle ampiezze
degli angoli riportati sia sul disegno
che a sinistra: sono tutti uguali a
due a due.
Una volta individuato l’incentro è possibile
spostare il vertice C per ottenere triangoli di
tipo diverso e per verificare che l’incentro, al
contrario dell’ortocentro, in tutti i triangoli
cade sempre all’interno. Per spostare il vertice
C cliccate sul primo riquadro e poi su Muovi
(freccia rossa). Poi spostatevi su C e, tenendo
premuto il tasto sinistro del mouse, spostate
il vertice dove volete. Otterrete tutti i tipi di
triangoli che volete, sempre con l’incentro
all’interno.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività 3
Le mediane nei triangoli
Tipologia: attività laboratoriale con costruzione di modelli in cartoncino di triangoli di diverso
tipo e relativa individuazione delle mediane.
Obiettivo didattico: lo scopo di questa attività è di far costruire e visualizzare concretamente
le mediane perché, come afferma la Castelnuovo: “più tempo i nostri ragazzi avranno dato allo
studio del concreto, quanto più tempo avranno perduto nell’osservare, tanto meglio
passeranno dopo alla comprensione delle forme astratte”.
(Didattica della matematica p.75)
Tempo: 3 ore (1 ora + 2 ore)
Fase 1
Fate costruire a ogni alunno tre triangoli
di cartoncino, uno acutangolo, uno
rettangolo e uno ottusangolo (Foto 1).
Anche in questo caso è meglio che
ciascun alunno disegni un triangolo
diverso dai suoi compagni in modo da
avere una maggiore quantità di esempi
e
poter
quindi
effettuare
delle
generalizzazioni.
La misura di almeno due dei lati di
ciascun triangolo dovrebbe essere un
numero
intero
per
facilitare
la
costruzione delle mediane.
Foto 1: i triangoli
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Triangolo acutangolo
Triangolo rettangolo
Con l’aiuto di un righello tracciate
con una matita, su ogni triangolo,
le tre mediane e trovate il
baricentro (Foto 2).
Fate le vostre osservazioni.
Triangolo ottusangolo
Foto 2: le mediane e il baricentro
Prendete un ago in cui avete fatto passare del
filo da cucire colorato a cui avete fatto un
piccolo nodo sul fondo e bucate il triangolo in
corrispondenza del baricentro (Foto 3).
Appendete il triangolo al filo. Se il baricentro
è costruito con precisione, il triangolo
dovrebbe restare in posizione orizzontale
(Foto 4).
Foto 3: il baricentro nel triangolo acutangolo
Foto 4: il triangolo acutangolo appeso per il baricentro
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fate ripetere lo stesso procedimento sul triangolo rettangolo (Foto 5) e sul triangolo
ottusangolo (Foto 6).
Foto 5: il triangolo rettangolo appeso per il baricentro
Foto 6: il triangolo ottusangolo appeso per il baricentro
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fase 2
In questa seconda fase, la costruzione delle mediane viene fatta utilizzando Geogebra.
Per l’apertura del file, seguite le istruzioni fornite all’inizio della Fase 2 dell’Attività 1.
Costruite (e fate costruire ai vostri
studenti) un triangolo qualsiasi oppure
uguale a quello da cui siete partiti per
tracciare le altezze, partendo dal riquadro
Poligono.
Ora dovete tracciare le mediane. Cliccate
con il tasto sinistro del mouse sull’angolino
in basso a destra del riquadro indicato dalla
freccia e poi su Punto medio o centro.
Cliccate, con il tasto sinistro del mouse, sul
segmento a, poi sul segmento b e infine sul
segmento c.
Successivamente cliccate sul riquadro indicato
dalla freccia e poi su Segmento tra due punti.
Cliccate su ciascun vertice e sul punto medio
del lato opposto corrispondente (A con D, B
con E, C con F).
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Individuate il baricentro cliccando sul riquadro
indicato dalla freccia e poi su Intersezione tra
due oggetti.
Una volta individuato il baricentro è possibile spostare il vertice C (o i vertici A e B) per
ottenere triangoli di tipo diverso e per verificare che il baricentro, come l’incentro, in tutti i
triangoli cade sempre all’interno. Per spostare il vertice C cliccate sul primo riquadro e poi su
Muovi (freccia rossa). Poi spostatevi su C e, tenendo premuto il tasto sinistro del mouse,
spostate il vertice dove volete. Otterrete tutti i tipi di triangoli che volete, sempre con l’incentro
all’interno.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fate scoprire agli studenti un’altra caratteristica del baricentro, quella cioè di dividere la
mediana in due parti di cui una è doppio dell’altra.
Fate
misurare
loro
la
distanza tra il baricentro e
un vertice e tra il baricentro
e il punto medio del lato
opposto a quel vertice.
Per
misurare
questa
distanza,
cliccate
sul
riquadro
indicato
dalla
freccia rossa e poi su
Distanza.
Seguite
le
istruzioni. Vi appariranno i
valori sia sul disegno che
sulla sinistra. Provate anche
con gli altri vertici e fate
trarre le conclusioni ai vostri
studenti.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività 4
Gli assi nei triangoli
Tipologia: attività laboratoriale con costruzione di modelli in carta di triangoli di diverso tipo e
relativa individuazione degli assi.
Obiettivo didattico: lo scopo di questa attività è di far costruire e visualizzare concretamente
gli assi perché, come afferma la Castelnuovo: “più tempo i nostri ragazzi avranno dato allo
studio del concreto, quanto più tempo avranno perduto nell’osservare, tanto meglio
passeranno dopo alla comprensione delle forme astratte”.
(Didattica della matematica p.75)
Tempo: 3 ore (1 ora + 2 ore)
Fase 1
Su fogli A4, fate disegnare e ritagliare a
ogni alunno tre triangoli di carta, uno
acutangolo,
uno
rettangolo
e
uno
ottusangolo (Foto 1). Possono anche
essere uguali a quelli costruiti nell’Attività
2. Il triangolo ottusangolo deve essere
ritagliato solo su due lati. Il terzo lato,
quello più lungo non deve essere
ritagliato.
Anche in questo caso è meglio che ciascun
alunno disegni triangoli diversi da quelli
disegnati dai suoi compagni in modo da
avere una maggiore quantità di esempi e
poter
quindi
effettuare
delle
generalizzazioni.
Foto 1: i triangoli
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Prendete
il
primo
triangolo (nella Foto 2a è
il triangolo acutangolo) e
dividete manualmente un
lato
perfettamente
a
metà,
piegando
il
triangolo in due parti
uguali in modo che due
vertici coincidano.
Foto 2a: la costruzione degli assi
Ripetete lo stesso procedimento per gli altri due lati
(Foto 2b).
Foto 2b: la costruzione degli assi
Circocentro
Asse 3
Una volta terminata questa operazione, che cosa potete far
notare agli studenti? Anche gli assi si incontrano tutti in un
unico punto: il circocentro (Foto 3).
Asse 2
Asse 1
Foto 3: il circocentro nel triangolo acutangolo
Stefania Pozio
Circocentro
Incentro
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Asse 3
Bisettrice 3
Asse 2
Fate ripetere lo stesso procedimento sul
triangolo rettangolo (Foto 4). Dove si trova il
circocentro?
Bisettrice 1
Asse 1 2
Bisettrice
Foto 4: il circocentro nel triangolo rettangolo
Asse 3
Circocentro
Asse 2
Asse 1
Foto 5: il circocentro nel triangolo ottusangolo
Fate ripetere lo stesso procedimento sul
triangolo ottusangolo (Foto 5). Dove si trova
il circocentro?
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Mettete
piegati.
vicini
i
tre
triangoli
Discutete con gli studenti sulle
differenze tra i vari tipi di triangoli.
Nel
triangolo
acutangolo,
il
circocentro è interno, in quello
rettangolo coincide con la metà
dell’ipotenusa,
in
quello
ottusangolo è esterno. Quindi il
circocentro si comporta come
l’ortocentro (Foto 6).
Foto 6: i tre triangoli piegati
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fase 2
In questa seconda fase, la costruzione degli assi viene fatta utilizzando Geogebra.
Per l’apertura del file, seguite le istruzioni fornite all’inizio della Fase 2 dell’Attività 1.
Costruite (e fate costruire ai vostri
studenti) un triangolo qualsiasi cliccando
sul riquadro Poligono.
Ora costruite gli assi. È molto
semplice. Cliccate con il tasto
sinistro del mouse sull’angolino in
basso a destra del riquadro
indicato dalla freccia e poi su
Asse di un segmento. Cliccate,
con il tasto sinistro del mouse,
sul lato a, poi sul lato b e infine
sul lato c per ottenere i tre assi.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Una volta trovati i tre assi, per
poter individuare il circocentro
dovete cliccare sul riquadro
Intersezione
tra
due
punti.
Spostatevi sul circocentro e
cliccate su ciascun asse. Vi
apparirà il circocentro.
Cliccate sul primo riquadro e poi su Muovi
(freccia rossa). Spostatevi con il mouse
sul punto C (o sul punto A o sul punto B)
e, tenendo premuto il tasto sinistro del
mouse spostate il vertice.
Che cosa notate?
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Fate misurare con il comando Distanza, la distanza del circocentro da ciascun vertice. Che cosa
notate? Se queste distanze sono tutte uguali, che cosa possiamo concludere?
Fase 3
Possiamo concludere che il punto di incontro degli assi si chiama circocentro perché
rappresenta il centro della circonferenza circoscritta al triangolo, cioè la circonferenza che
passa per i suoi tre vertici.
Con l’aiuto di Geogebra, troviamo
questa circonferenza. È molto facile.
Cliccate sul riquadro indicato dalla
freccia rossa e poi su Circonferenza
per tre punti.
Cliccate sui tre vertici del triangolo.
Se, una volta trovata la
circonferenza non dovreste
riuscire a visualizzarla tutta,
come nel caso del disegno qui
a fianco, cliccate sull’ultimo
riquadro e poi su Muovi la
Vista Grafica. A questo punto
posizionatevi
sulla
circonferenza
e,
tenendo
premuto il tasto sinistro del
mouse,
trascinate
la
circonferenza verso il basso in
modo da visualizzarla tutta.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Una volta ottenuta la
circonferenza, cliccare sul
primo riquadro, poi su
Muovi. Poi spostatevi su
C e, tenendo premuto il
tasto sinistro del mouse,
spostate il vertice dove
volete. Potrete osservare
che
la
circonferenza
rimane
sempre
all’esterno.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività per le eccellenze
La retta di Eulero
La Retta di Eulero è la retta passante per l'ortocentro, il baricentro e il circocentro di un
triangolo.
Fate disegnare un triangolo qualsiasi ai vostri studenti e fate trovare loro l'ortocentro, il
baricentro e il circocentro secondo le istruzioni delle Attività precedenti.
Baricentro
Circocentro
Ortocentro
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Con
il
comando
Mostra/nascondi (illustrato a
pag. 3 delle Attività per le
eccellenze
circonferenza
inscritta) nascondete tutte le
altezze, gli assi e le mediane
fino ad ottenere questa figura
in cui appaiono solo i punti
medi e i tre punti notevoli.
Cliccate sul riquadro indicato dalla
freccia e poi su Retta per due
punti. Cliccate sui punti G e H.
Ottenete la retta di Eulero.
Retta di Eulero
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Spostate il vertice C e osservate con gli studenti i diversi spostamenti della retta di Eulero e,
ovviamente, dei tre punti notevoli.
Fate trovare agli studenti anche l’incentro e discutete con loro sui risultati ottenuti.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Attività per le eccellenze
Come trovare la circonferenza inscritta in un triangolo
Una caratteristica dell’incentro è di essere equidistante da tutti i lati del triangolo, cioè di
mantenere sempre la stessa distanza da ogni lato. Fate verificare questo ai vostri alunni.
Come?
Innanzitutto ricordate loro il concetto di distanza. Che cosa indica la distanza di un punto da un
segmento? Indica la perpendicolare condotta dal punto alla retta (o al segmento). Quindi,
troviamo nel nostro disegno, le tre perpendicolari che partendo dall’incentro arrivano su
ciascun lato.
Cliccate con il mouse sul riquadro
indicato dalla freccia rossa e poi su
Retta perpendicolare. Cliccate su D e
poi sul segmento a e vi apparirà la
prima perpendicolare. Poi cliccate su D
e poi sul segmento b e vi apparirà la
seconda perpendicolare, infine su D e
sul segmento c.
Individuate i punti di intersezione tra
ciascuna perpendicolare e il lato
corrispondente
cliccando
su
Intersezione tra due punti. Spostatevi
con il mouse sui punti di intersezione,
cliccateci sopra per individuarli.
Per essere sicuri di esservi posizionati
correttamente sul punto di intersezione,
assicuratevi
che
vi
appaia
questo
riquadro.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Per misurare la distanza tra
l’incentro e ciascun lato del
triangolo, cliccate sul riquadro
indicato dalla freccia rossa e poi
su Distanza. Vi appariranno i
valori sia sul disegno che sulla
sinistra.
I valori ovviamente sono identici.
L’incentro è il centro della circonferenza inscritta nel triangolo. Con l’aiuto di Geogebra,
disegniamo questa circonferenza.
Innanzitutto “puliamo” il disegno, cioè nascondiamo le rette e cancelliamo i valori delle
distanze.
Per cancellare i valori delle distanze sul disegno è
sufficiente posizionarsi sul testo, cliccare sul tasto
destro del mouse e poi su elimina.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Per “nascondere” le rette
cliccare
sull’ultimo
riquadro,
e
poi
su
Mostra/nascondi oggetti.
Cliccare su ogni retta (sono
6) finché non diventano
tutte e sei in grassetto e
poi cliccare sul primo
riquadro (freccia rossa). A
questo
punto
sia
le
bisettrici
che
le
perpendicolari
sono
nascoste.
Stefania Pozio
Altezze, mediane, bisettrici e assi: che cosa hanno di speciale?
Cliccare sul riquadro indicato dalla
freccia e poi su Circonferenza per
tre punti. Seguire le istruzioni,
cioè cliccare sui punti E, F e G.
Una
volta
ottenuta
la
circonferenza, cliccare sul primo
riquadro, poi su Muovi. Poi
spostatevi su C e, tenendo
premuto il tasto sinistro del
mouse, spostate il vertice dove
volete. Potrete osservare che la
circonferenza
rimane
sempre
all’interno.