1
“Laboratorio geometria-progetto SIGMA”
Sintesi dell’attività
Scuola secondaria di primo grado
a.s. 2013/14
Scuola: Scuola secondaria di I grado di Pergine Valdarno
Livello scolare: classe I scuola secondaria di I grado
Docente: Galli Alessandra
Descrizione dell’esperienza
La classe è poco numerosa (14 alunni) e i ragazzi hanno sommariamente un
comportamento collaborativo e disciplinato. Di fronte ad attività di tipo praticosperimentale, si sono inoltre sempre dimostrati curiosi ed entusiasti, mostrando di
apprendere più velocemente e in maniera produttiva se messi di fronte ad attività
laboratoriali.
Questo tipo di attività, che portava ad affrontare la parte di geometria relativa alle
isometrie, mi ha permesso di anticipare quella parte del programma che solitamente
ho sempre affrontato nelle classi seconde. Alla luce dei risultati a cui ha portato
questa esperienza, ritengo di avere fatto la cosa giusta, anche per una continuità con il
programma di tecnologia che i ragazzi stavano affrontando.
Ho visto alcuni disegni che i ragazzi avevano realizzato e, oltre alle costruzioni con
riga e compasso dei poligoni regolari, avevano anche affrontato alcuni tipi di
tassellazioni, che i ragazzi chiamavano “mattonelle”, attraverso la ripetizione di
motivi geometrici ricorrenti.
Ho pensato quindi di allacciarmi a quello che già stavano affrontando e spiegare le
trasformazioni isometriche tramite un programma, Geogebra, che i ragazzi non
avevano mai utilizzato e di cui hanno appreso l’importanza e la duttilità.
Nella pagina seguente sono riportati alcuni disegni realizzati durante le ore di
tecnologia con il prof. Falsini (poligoni regolari e tassellazioni geometriche).
2
Durata:
l’attività è stata svolta in 8 ore, di cui 3 svolte in classe e 5 affrontate tramite attività
al computer.
Materiali e strumenti: pc e LIM, cartoncini, forbici e colla.
Metodi: l’impostazione del lavoro è stata completamente laboratoriale.
Non sono stati affrontati definizioni o concetti puramente teorici, poiché sono stati
una conseguenza dell’osservazione e della realizzazione tramite l’utilizzo di
Geogebra.
Sono sempre state introdotte situazioni problematiche che hanno fornito l’innesco di
discussioni in cui ogni alunno ha potuto intervenire liberamente, rendendosi
consapevole del proprio apprendimento.
Ho cercato di guidare i ragazzi nel loro processo di scoperta, senza mai essere troppo
esplicita e senza mai anticipare i concetti, cercando di stimolare i loro interventi e la
loro curiosità.
Ho raggruppato l’attività in 3 fasi, la prima, svolta in classe, in cui i ragazzi hanno
avuto modo di manipolare con carta, forbici e colla, alcuni poligoni regolari per
scoprire il concetto di tassellazione, la seconda è stata la parte affrontata sul
computer, la terza è stata la fase in cui i ragazzi hanno effettuato una sorta di verifica
e una realizzazione di un esercizio di ripasso riassuntivo di tutti i concetti che
avevamo affrontato.
E’ stato svolto un incontro con la collega, Prof.ssa Gianna Corradeschi, anch’essa
coinvolta nel progetto SIGMA, in cui sono state concordate le modalità e i metodi di
lavoro.
3
Fase I (3 ore)
In questa fase, ho assegnato ai ragazzi alcune fotocopie in cui erano rappresentati i
seguenti poligoni regolari aventi lo stesso lato:
Ho invitato i ragazzi a ritagliare questi poligoni e a tentare di posizionarli in modo
tale da riempire un intero foglio di carta senza lasciare spazi vuoti.
In questo modo i ragazzi hanno avuto modo di esplorare quali poligoni avessero le
caratteristiche necessarie per poter ricoprire completamente un piano.
Dopo vari tentativi, i ragazzi hanno capito che il pentagono non permetteva di
tassellare:
tentativo di tassellazione fallito!
Riguardo al pentagono è stata fatta una discussione sul perché non permettesse di
tassellare un piano. Dopo qualche ipotesi e un piccolo aiuto da parte mia, i ragazzi
sono arrivati alla conclusione che per arrivare a una tassellazione, intorno ad un
vertice ci devono stare angoli che sommati insieme devono dare 360°, l’angolo giro.
4
In classe poco tempo prima avevamo affrontato il calcolo degli angoli interni di un
poligono, quindi, i ragazzi, hanno capito che essendo la somma degli angoli interni
del pentagono 540°, questo poligono non permetteva di perseguire gli scopi che ci
eravamo prefissati.
Dopo alcuni tentativi, i ragazzi sono arrivati alle seguenti composizioni di poligoni:
5
Fase II (4 ore)
La seconda fase del progetto, è stata abbastanza complicata per un problema logistico
e organizzativo. Infatti, nella nostra scuola abbiamo avuto dei problemi ai computer,
ma sono comunque riuscita a trovare una scappatoia e a concludere il progetto,
tramite l’utilizzo di alcuni pc portatili, della scuola, miei e dei colleghi che si sono
dimostrati molto collaborativi da questo punto di vista.
Ho diviso i ragazzi in piccoli gruppi e siamo quindi riusciti a concludere l’attività
improvvisando un laboratorio di informatica in classe. E’ stato curioso vedere come i
ragazzi si siano dimostrati entusiasti e collaborativi anche nell’affrontare questa
nuova emergenza, tanta era la curiosità di imparare ad utilizzare questo nuovo
programma.
Ho mostrato alla LIM la schermata principale di Geogebra, invitandoli ad esplorare
senza limiti i comandi del programma.
Dopo questa prima fase, in cui i ragazzi si sono molto divertiti, ho proposto ai ragazzi
di fare su Geogebra le tassellazioni che avevano loro stesso individuato con le
costruzioni con carta, forbici e colla.
Ho dovuto necessariamente spiegare il minimo indispensabile su come creare i vettori
per effettuare traslazioni e simmetrie e ho lasciato i ragazzi liberi di esplorare le
modalità di costruzione dei poligoni.
Qui sotto sono proposte alcune tassellazioni da loro realizzate:
6
…..e qui sono proposte alcune immagini dei ragazzi al lavoro:
7
Durante la realizzazione di queste tassellazioni, ho chiesto ai ragazzi di provare a
spiegare il concetto di traslazione, simmetria assiale e simmetria centrale, che erano
le trasformazioni che avevano utilizzato con il programma.
Nonostante forse i termini specifici abbiano lasciato un po’ a desiderare, mi sono
accorta che tutti gli alunni, anche quelli che hanno sempre manifestato delle difficoltà
nella mia disciplina, avevano perfettamente capito il concetto di ogni trasformazione.
Mi sono quindi riproposta di affinare la parte relativa ai linguaggi specifici delle
isometrie una volta terminata l’attività sperimentale, invitandoli a proporre altre
definizioni che fossero più rigorose.
Sono comunque sicura che qualsiasi altra spiegazione sull’argomento non avrebbe
portato ad un più elevato apprendimento dei concetti principali.
Fase III (valutazione): 1 ora
In questa fase, gli alunni sono stati invitati e realizzare questa tassellazione tramite
l’utilizzo di tutte e tre le isometrie che avevamo affrontato (traslazione, simmetria
assiale e simmetria centrale).
8
I piccoli gruppi che avevo formato erano bilanciati per quanto riguardava le
predisposizioni alla disciplina e ho notato che tutti i gruppi, chi con meno tempo e chi
con più tempo, sono riusciti ad arrivare alla soluzione.
Non ho attribuito valutazioni numeriche, perché non amo dare una valutazione
rigorosa ai lavori di gruppo, e dato che tra ragazzi e pc non c’era un rapporto di 1: 1
ho preferito solo dare una valutazione sommaria che servisse a me per valutare quale
fosse stato l’apprendimento dell’argomento.
Comportamento degli studenti
Gli studenti hanno avuto un comportamento davvero esemplare. Si sono dimostrati
collaborativi sotto tutti i punti di vista, con me e con i compagni. Tutti hanno
contribuito alla realizzazione di un lavoro, anzi gli alunni più deboli venivano sempre
spronati dai compagni ad arrivare alle soluzioni.
Un fatto molto positivo è stato che questo progetto ha aiutato nell’integrazione di un
nuovo alunno, un ragazzo cinese arrivato nella classe a fine marzo, che non conosce
neanche una parola di italiano.
Attraverso il linguaggio universale dell’informatica e della geometria, è riuscito ad
entrare in sintonia con i suoi compagni di classe e a partecipare attivamente alle
attività.
Apprendimento: successi e difficoltà
L’unica difficoltà riscontrata è stata quella dovuta alla mancanza di mezzi informatici
adeguati che permettessero ad ogni studente di lavorare in autonomia. I successi sono
stati sicuramente molti di più e credo che in futuro l’utilizzo di questo programma
sarà un passo obbligato ogni volta che dovrò affrontare le trasformazioni isometriche.
9
Scuola: Scuola secondaria di I grado di Bucine
Classe: II A
Docente: Corradeschi Gianna Maria
Descrizione dell’esperienza
Ho scelto di svolgere questa esperienza nella classe II sez A della Scuola Secondaria
di I grado di Bucine, perché nel periodo antecedente all’attività gli alunni avevano
affrontato lo studio dei poligoni e delle loro proprietà .
Inoltre questi studenti, di fronte ad attività di tipo pratico-sperimentale, si sono
sempre dimostrati curiosi ed entusiasti, mostrando di apprendere più velocemente e in
maniera produttiva se messi di fronte ad attività laboratoriali.
Questo tipo di attività ha permesso di affrontare le trasformazioni isometriche in
modo divertente e cioè utilizzando il programma Geogebra che gli alunni hanno
imparato velocemente ad utilizzare, mostrandosi motivati all’apprendimento, molto
di più che attraverso la lezione frontale e la lettura del libro di testo.
Il lavoro svolto dall’ insegnante di scienze matematiche è stato il più possibile
interdisciplinare infatti l’insegnante di tecnologia ha ripreso con i ragazzi la
costruzione tecnica dei poligoni regolari e le tassellazioni, che gli alunni chiamano
“mattonelle”, argomenti affrontati lo scorso anno scolastico. (Fig.1-Fig.2-Fig.3)
Fig. 1
10
Fig. 2
Fig.3
Durata:
l’attività è stata svolta in 8 ore, di cui 3 svolte in classe e 5 nel laboratorio di
informatica
Materiali e strumenti: pc e LIM, cartoncini, matite colorate, forbici e colla.
Metodi: l’impostazione del lavoro è stata completamente laboratoriale.
11
Non sono stati affrontati definizioni o concetti puramente teorici, poiché sono stati
una conseguenza dell’osservazione e della realizzazione tramite l’utilizzo di
Geogebra.
Fin dall’inizio gli argomenti sono sempre stati proposti come problem-solving in cui
ogni alunno è potuto intervenire liberamente, rendendosi consapevole del proprio
apprendimento.
Ho cercato di guidare i ragazzi nel loro processo di scoperta senza mai anticipare i
concetti, le regole o le proprietà, cercando di stimolare i loro interventi e la loro
curiosità.
E’ stato svolto un incontro con la collega Prof.ssa Alessandra Galli, anch’essa
coinvolta nel progetto SIGMA, in cui sono state concordate le modalità e i metodi di
lavoro.
Ho suddiviso l’attività in 3 fasi, la prima, svolta in classe, in cui i ragazzi hanno avuto
modo di manipolare con carta, forbici e colla, alcuni poligoni regolari per scoprire il
concetto di tassellazione, la seconda si è svolta nel laboratorio di informatica, la terza
è stata la fase in cui i ragazzi hanno effettuato una sorta di verifica e valutazione del
lavoro svolto, cioè hanno eseguito una tassellazione in modo individuale e autonomo,
verificando se i concetti erano stati effettivamente appresi.
Fase I (3 ore)
In questa fase, ho assegnato ai ragazzi ( che lavoravano in coppie ) alcune fotocopie
in cui erano rappresentati i seguenti poligoni regolari aventi il lato della stessa
misura:
Ho scritto sulla lavagna alcune domande, che gli alunni hanno trascritto via via sul
quaderno. Ogni gruppo ha scritto la propria risposta che è stata discussa insieme:
• Riconosci poligoni a te familiari? Tutti hanno risposto triangolo, quadrato,
pentagono, esagono e ottagono
12
• Che cosa hanno in comune questi poligoni? Molti hanno risposto, dopo aver
misurato i lati, che avevano tutti i lati uguali, sia nello stesso poligono, che i
poligoni tra loro.
• Come si potrebbero chiamare tutti questi poligoni? Alcuni hanno risposto
“regolari”
• Significa soltanto che hanno i lati congruenti? Alcuni hanno detto che anche gli
angoli dovevano essere uguali, portando l’esempio del quadrato e del
triangolo equilatero, 90° e 60°, che già conoscevano.
• Colorate con lo stesso colore i poligoni con la stessa forma(Fig.4- Fig.5)
Fig.4
13
Fig.5
Ho invitato i ragazzi a ritagliare questi poligoni. Anche i due alunni con il sostegno e
i due alunni DSA sono riusciti da soli a seguire tutte le fasi dell’attività. (Fig.6-Fig.7)
Fig.6
14
Fig.7
Successivamente agli alunni è stato chiesto di posizionare i poligoni in modo tale da
riempire un intero foglio di carta senza lasciare spazi vuoti.
Ho portato l’esempio di un muratore che deve piastrellare un pavimento. Un ragazzo
ha osservato che se il muratore fa un pavimento con degli spaziettini vuoti poi il
cliente non glielo paga!...un altro alunno ha aggiunto che nemmeno si può tagliare
un pezzetto di mattonella, altrimenti il mosaico del pavimento viene storto!
Così, dopo vari tentativi, molti ragazzi hanno capito che il pentagono non permetteva
di tassellare il piano. Un alunno ha osservato che solo con il pentagono, se si volesse
per forza far combaciare i suoi lati, la superficie del pavimento si incurverebbe!.Ho
suggerito di osservare bene il disegno per capire perché solo con il pentagono
rimaneva uno spazio vuoto. (Fig.8) Un alunno ha fatto un’osservazione, che è stata
acclamata da tutti, e cioè che intorno ad un vertice ci dovevano stare angoli che
sommati insieme dovevano dare 360°, l’angolo giro. Alcuni alunni hanno chiesto ad
altri se si ricordavano come si faceva a calcolare gli angoli interni del pentagono.
Dopo un po’ di discussione qualcuno ha pensato di dividere il pentagono in triangoli
e moltiplicare 180° per tre e poi dividere per 5. Hanno trovato 108°. E poi con lo
stesso metodo hanno calcolato anche l’ampiezza degli angoli interni
dell’esagono(120°) e dell’ottagono(135°).Un gruppo di alunni ha cercato, con i
calcoli, di combinare le ampiezze degli angoli per ottenere 360° ed è arrivato alla
conclusione che con i 108° non è possibile.
15
Fig.8
Fig.9
In questo modo hanno avuto modo di scoprire quali poligoni avessero le
caratteristiche necessarie per poter ricoprire completamente un piano. (Fig.9)
Unendo tutti i poligoni dei vari gruppi hanno cercato di pavimentare tutta la
superficie del banco. ( Fig.12)
16
Fig.10
Fig.11
17
Fig.12
Fase II (4 ore)
Nella seconda fase del progetto, in cui i ragazzi si sono molto divertiti, ho mostrato
alla LIM la schermata principale di Geogebra, invitandoli a turno a provare i comandi
del programma utili per il nostro lavoro.
Poi ho portato gli alunni nel laboratorio di informatica dove ci sono 11 macchine,
quindi essendo 22, in ogni computer hanno lavorato 2 alunni. Gli alunni con sostegno
sono stati seguiti, in questa fase, dall’ insegnante di sostegno e da un compagno
adeguato per capacità e carattere. (Fig.13-Fig.14-Fig.15)
Ho proposto quindi ai ragazzi di fare su Geogebra le stesse tassellazioni che avevano
costruito con carta, forbici.
Ho spiegato il minimo necessario per creare i vettori per effettuare traslazioni,
simmetrie assiali e centrali, poi ho lasciato i ragazzi liberi di esplorare le modalità di
costruzione dei poligoni.
18
Fig.13
Fig.14
19
Fig.15
Queste sono alcune tassellazioni realizzate dagli alunni
Fig.16
20
Fig.17
Fig.18
21
Fig.19
Durante la realizzazione di queste tassellazioni, ho chiesto ai ragazzi di provare a
spiegare il concetto di traslazione, simmetria assiale e simmetria centrale, che erano
le trasformazioni che avevano utilizzato con il programma.
Nonostante forse i termini specifici abbiano lasciato un po’ a desiderare, tutti gli
alunni, anche quelli che hanno sempre manifestato delle difficoltà nelle discipline
scientifiche, avevano perfettamente capito il concetto di ogni trasformazione
isometrica.
Mi sono quindi riproposta di affinare la parte relativa ai linguaggi specifici delle
isometrie una volta terminata l’attività sperimentale, invitandoli a proporre altre
definizioni che fossero più rigorose.
Sono comunque sicura che qualsiasi altra lezione frontale sull’argomento non
avrebbe portato ad un livello di apprendimento dei concetti principali così elevato.
Fase III (valutazione): 1 ora
In questa fase, gli alunni sono stati invitati e realizzare in modo autonomo questa
tassellazione tramite l’utilizzo di tutte e tre le isometrie che avevamo affrontato
(traslazione, simmetria assiale e simmetria centrale).
22
Fig.20
Fig.21
I piccoli gruppi che avevo formato erano studiati in modo che le abilità fossero
bilanciate e ho notato che tutti, più o meno velocemente, sono riusciti ad arrivare alla
soluzione.
Non ho attribuito nessuna valutazione di merito. L’obiettivo è stato completamente
raggiunto da tutti.
Comportamento degli studenti
Gli studenti hanno avuto un comportamento davvero esemplare. Si sono dimostrati
collaborativi sotto tutti i punti di vista, con me e con i compagni. Tutti hanno
contribuito alla realizzazione di un lavoro, anzi gli alunni più deboli sono stati sempre
spronati dai compagni ad arrivare alle soluzioni.
Apprendimento: successi e difficoltà
Nessuna difficoltà da segnalare.
L’attività ha avuto molto successo e credo che in futuro riproporrò sicuramente
questa stessa attività e utilizzerò il programma Geogebra non solo per comprendere le
trasformazioni isometriche ma anche per altre applicazioni geometriche
23
Scuola: Scuola secondaria di I grado “ R. Magiotti” di Montevarchi
Classe: III C
Docente: Mario Petrillo
La classe, composta da 26 alunni, ha svolto le attività previste dal progetto nel
periodo Febbraio-Aprile 2014, lavorando con cadenza settimanale.
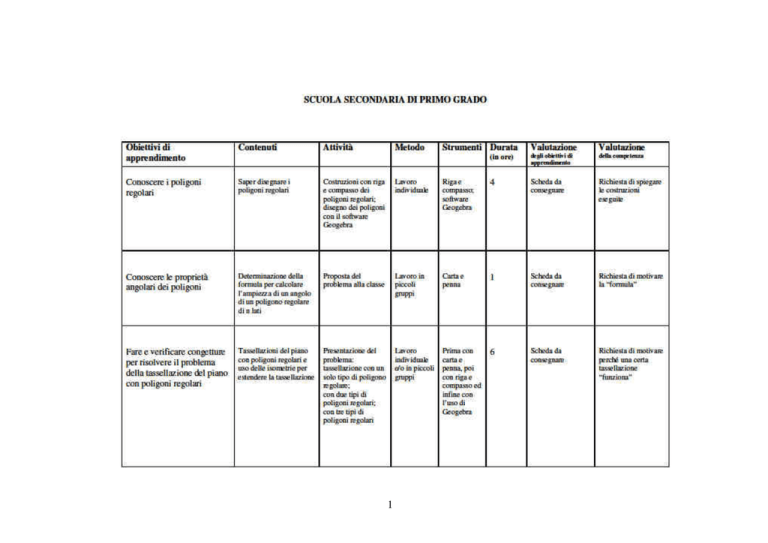
Inizialmente è stato presentato il progetto-laboratorio e il significato di tassellazione
del piano con poligoni regolari mediante l’uso delle isometrie; quindi sono state
riprese le costruzioni con riga e compasso di alcuni poligoni regolari: triangolo
equilatero, quadrato, pentagono, esagono, ottagono.
A seguire, nel laboratorio di informatica, è stato introdotto l’uso del software
Geogebra per disegnare i poligoni ed applicare ad essi le principali isometrie.
Successivamente, lavorando a piccoli gruppi, è stata affrontato il seguente quesito:
“Con quali poligoni regolari è possibile ricoprire esattamente il piano?”
Si è lasciato in un primo momento che i gruppi lavorassero come volevano (la
maggior parte hanno fatto disegni “a mano libera”): dalla discussione collettiva e
dalla considerazione del fatto che in ogni vertice la somma degli angoli dovesse
essere 360° è emerso che alcune delle tassellazioni trovate erano sicuramente corrette
mentre altre erano errate.
Per dare un po’ di ordine al lavoro l’insegnante ha chiesto di concentrarsi prima sulle
tassellazioni con un solo tipo di poligono regolare, poi su quelle con due tipi e infine
con tre tipi di poligoni regolari, facendo inoltre in modo che tutti i vertici fossero
dello stesso “tipo” cioè che vi convergesse lo stesso numero e tipo di poligoni.
Dopo aver provato a “mano libera” e poi con riga e compasso, gli studenti hanno
utilizzato il software Geogebra e gradualmente sono state “scoperte” alcune possibili
tassellazioni sia con un solo tipo di poligono, che con due e/o con tre poligoni
regolari diversi ma con il lato della stessa misura. Alcuni studenti hanno anche
colorato i poligoni per ottenere un effetto “artistico”; altri si sono concentrati nel
provare la “combinazione” giusta di angoli interni intorno ad un vertice e quindi sono
state utili le “formule” per il calcolo dell’angolo interno dei vari poligoni regolari.
Tali relazioni sono state ricavate in classe lavorando sia sulla suddivisione dei
poligoni in triangoli, sia considerando gli angoli esterni e i supplementari interni. Il
pentagono è stato il guastafeste delle tassellazioni, infatti solo usandolo con i
decagono sono riuscite delle “strisce” (usando la traslazione orizzontale) ma è
risultato impossibile coprire il piano.
24
In conclusione direi che il problema proposto e il metodo di lavoro in piccoli gruppi è
stato stimolante per gli studenti che hanno sempre partecipato con entusiasmo alle
attività proposte.
Inoltre gli obiettivi di apprendimento sono stati raggiunti per la maggior parte degli
studenti e l’aspetto sicuramente più formativo dell’attività è stato senza dubbio quello
di poter fare congetture e metterle alla prova con l’uso di Geogebra.
Immagini dal laboratorio di tassellazione: dalla lavagna a Geogebra
Con quali poligoni regolari possiamo “ricoprire” perfettamente il piano facendo
coincidere lato con lato e vertice con vertice?
Tassellazione con un solo tipo di poligono regolare
Considerazioni in classe sulle isometrie da usare con il triangolo equilatero e
tassellazioni fatte sulla carta con righello e compasso
25
26
27
Se usiamo solo un tipo di poligono regolare quali sono quelli con cui posso
“tassellare” il piano?
Fai le tue congetture e verificale con Geogebra.
Suggerimento: l’angolo interno di un triangolo equilatero misura 60°, l’angolo
interno di un quadrato misura 90°…….
Nota
Una volta capito quali poligoni regolari puoi usare, per ricoprire il piano puoi
utilizzare traslazioni, rotazioni, simmetrie assiali ….
Indica quali isometrie hai utilizzato per “estendere” la tua tassellazione.
Vignani Cecilia
Anna Boschi
28
“Tassellazioni” con due tipi di poligoni regolari
Se possiamo usare come “mattonelle” della nostra pavimentazione due tipi di
poligoni regolari: quali sono le combinazioni che funzionano?
Scrivi una tabella con il valore degli angoli interni dei vari poligoni regolari… (vedi
scheda alunni)
Ci sono altre combinazioni?
Triangoli equilateri ed esagoni regolari
in questo caso i vertici non sono tutti dello stesso tipo….)
quadrato e ottagono regolare
triangolo equilatero e dodecagono regolare
29
“Tassellazioni” con tre tipi di poligoni regolari
(anche con vertici non tutti dello stesso “tipo”)
Dodecagono, quadrato e triangolo
esagono, quadrato e triangolo
30
Tassellazione a “fiocco di neve” con triangolo quadrato ed esagono
Traslazioni per una tassellazione con quadrato, esagono e dodecagono
31
Lavori degli studenti
L’ANGOLO INTERNO
È necessario cominciare questo lavoro col dire che parleremo, oltre che di poligoni e
combinazioni tra di loro, anche, anzi soprattutto, degli angoli interni dei poligoni.
Vanno considerati con grande importanza per capire bene quali poligoni possono essere
accostati fra di loro fino a formare una tassellazione corretta e completa.
La somma degli angoli esterni di un poligono è SEMPRE 360°. La somma dell’angolo
esterno e del suo supplementare è SEMPRE di 180° (angoli adiacenti).
Qual è la relazione che mi permetterebbe di calcolare l’angolo interno di un
poligono?
Abbiamo bisogno di conoscere l’ampiezza dell’angolo interno perché, nella
tassellazione, la somma degli angoli interni usati deve essere 360°!
Quindi: angolo E + angolo I = 180°; somma angoli E = 360°
I = 180°-360°/n n = n° lati
C’è anche un’altra modalità per calcolare l’angolo interno: per ogni vertice “partono” un
numero di diagonali pari a n-3. Il poligono viene così suddiviso in triangoli, ognuno dei
quali ha come somma degli angoli interni 180°.
Quindi: I = [180°X(n-2)]/n
TABELLA ANGOLI INTERNI DEI POLIGONI
NOME POLIGONO N° LATI ANGOLO I
Triangolo
3
60°
Quadrato
4
90°
Pentagono
5
108°
Esagono
6
120°
Eptagono
7
128°34’
Ottagono
8
135°
Ennagono
9
140°
Decagono
10
144°
Endecagono
11
147°16’
Dodecagono
12
150°
Ottadecagono
18
160°
Decadecagono
20
162°
32
TASSELLAZIONE CON TRIANGOLI EQUILATERI
Per tassellare usando solamente dei triangoli equilateri
ho:
1. disegnato il triangolo equilatero di riferimento;
2. tracciato un vettore orizzontale per traslare il
poligono iniziale;
3. traslato in linea orizzontale il triangolo per 9 volte;
4. tracciato un vettore obliquo inclinato a 60° per
traslare il poligono in direzione obliqua;
5. disegnato il simmetrico del triangolo ottenuto
rispetto al suo lato orizzontale;
6. traslato in orizzontale l’ultimo triangolo disegnato
per 8 volte;
7. continuato traslando i triangoli in orizzontale e
obliquo.
OSSERVAZIONE: sono possibili alcune tassellazioni con un solo poligono ripetuto più
volte. Le possibili tassellazioni possono essere fatte solo con triangoli (vedi sopra),
quadrati e esagoni. Sono possibili anche tassellazioni con solo due poligoni ripetuti più
volte: queste sono ottenute con triangolo e quadrato, triangolo e esagono, ottagono
e quadrato, dodecagono e triangolo e pentagono e decagono (vedi tutte sotto).
NOTA BENE: per essere certi che la combinazione funzioni, i poligoni usati devono
avere la stessa misura del lato.
QUALCHE COMBINAZIONE:
6 triangoli:
• tracciato triangolo;
• ruotato triangolo per 5 volte, così da ottenere la
tassellazione correttamente completa.
2 ottagoni + 1 quadrato:
• tracciato ottagono;
• traslato ottagono secondo vettore;
• tracciato quadrato per congiungere le basi dei due
ottagoni.
33
1 decagono + 2 pentagoni:
• tracciato decagono;
• tracciato pentagono su lato del decagono;
• ruotato pentagono tutto intorno al decagono.
Questa combinazione fa eccezione rispetto alle altre: è
eseguibile solo singolarmente, perché i suoi pentagoni non
si possono combinare ad altri per formare una riga
completa di tassellazione.
2 esagoni + 2 triangoli:
• tracciato esagono;
• tracciato simmetrico centrale al punto evidenziato;
• tracciato triangolo equilatero su lato dell’esagono;
• tracciato simmetrico centrale al punto dato.
34
Abbiamo iniziato a conoscere il mondo delle TASSELLAZIONI. In classe, con un foglio, le
squadre, il compasso e il goniometro, ci siamo messi a studiare dei possibili modi di tassellare il
piano con le isometrie di poligoni regolari.
Abbiamo iniziato a lavorare basandoci su un triangolo (ovviamente, equilatero) e abbiamo scoperto
vari modi di procedere.
MODI DI PROCEDERE:
-Fare 5 rotazioni di 60° in senso
antiorario, così da formare un esagono;
traslare poi il centro della rotazione
della lunghezza del lato di base verso
destra parallelamente al lato di base.
Poi, ricominciare con 4 rotazioni.
-Effettuare simmetrie assiali rispetto ai
lati stessi del triangolo.
Siamo passati poi a lavorare su un quadrato e abbiamo confermato, anche in questo, vari modi di
procedere, molto simili a quelli utilizzati per il triangolo.
35
MODI DI PROCEDERE:
-Fare 3 rotazioni di 90° in senso
antiorario, così da formare un altro
quadrato più grande; traslare poi il
vertice di rotazione della lunghezza del
lato di base verso destra parallelamente,
appunto, al lato di base. Ricominciare,
dunque, con le 3 rotazioni.
-Effettuare simmetrie assiali rispetto ai
lati stessi del quadrato.
Così, per facilitarci il lavoro, ci siamo costruiti una tabella compilata con le misure degli angoli
interni di ciascun poligono.
NOME POLIGONO
N. LATI ANGOLO INTERNO
(n)
Gradi Primi Secondi
TRIANGOLO
3
60°
0’
0”
QUADRATO
4
90°
0’
0”
PENTAGONO
5
108°
0’
0”
ESAGONO
6
120°
0’
0”
ETTAGONO
7
128°
34’
12”
OTTAGONO
8
135°
0’
0”
ENNAGONO
9
140°
0’
0”
DECAGONO
10
144°
0’
0”
ENDECAGONO
11
147°
16’
12”
DODECAGONO
12
150°
0’
0”
TRIDECAGONO
13
152°
18‘
36“
TETRADECAGONO
14
154°
17’
24”
PENTADECAGONO
15
156°
0’
0”
ESADECAGONO
16
157°
30’
0”
ETTADECAGONO
17
158°
49’
12”
OTTADECAGONO
18
160°
0’
0”
ENNADECAGONO
19
161°
3’
0”
ICOSAGONO
20
162°
0’
0”
36